Настоящее сочинение является восьмым независимым выпуском из серии работ, предпринятых автором над общим заглавием „Межпланетные сообщения“.
Семь выпусков уже вышли в свет, а именно:
Выпуск I. „Мечты, легенды и первые фантазии“ Лгр. 1928.
„
II. „Космические корабли в фантазиях романистов“. Лгр. 1928.
„
III. „Лучистая энергия в фантазиях романистов и в проектах ученых“ — Лгр. 1931.
„
IV. „Ракеты“ — Лгр. 1929.
„
V. „Теория реактивного движения“ — Лгр. 1929.
„
VI. „Суперавиация и суперартиллерия“ Лгр. 1929.
„
VII. К. Э. Циолковский „Его жизнь, работы и ракеты“ Лгр. 1931.
Последний, девятый, выпуск „Астронавигация. Летопись, библиография и указатели имен и предметов“ печатается.
Все замечания по поводу вышедших в свет выпусков и требования о высылке их читатели благоволят направлять автору по адресу:
Ленинград, Коломенская ул. 37 кв 25.
Николаю Алексеевичу Рынину.
Ленинград.
Настоящий выпуск, озаглавленный „Теория космического полёта“ заключает в себе собрание переводов и изложений классических работ по этому вопросу, главным образом, иностранных авторов и некоторых русских.
Излагаются работы: французских ученых — Эсно-Пельтри (три статьи) и М. Руа, американца — Годдара, немецких ученых — Оберта, Гоманна, Лоренца, Шершевского, Кунца, Пирке, Дебуса и Лей, русских — Кондратюка и Лебедева. В заключение приводится описание наших опытов по исследованию эффекта ускорения на живые организмы.
Заметим, что изложение работ многих других ученых, как русских, так и иностранных, вошло в ранее изданные выпуски нашей серии. В частности, работам К. Циолковского был посвящен специальный седьмой выпуск. Изучение работ, посвященных проблеме межпланетных сообщений и помещенных в настоящем выпуске, показывает, что в разных странах разные лица пришли независимо один от другого к одному и тому же заключению, что межпланетные сообщения возможны, но практическое осуществление их пока встречает ряд технических и финансовых затруднений. Однако, эти затруднения в будущем должны быть преодолены, и человек пробьет, наконец, мешающие его полету панцыри атмосферы и земного тяготения и унесется в загадочное и сулящее много новых впечатлений и открытий межпланетное пространство.
Нам известны всего четыре работы Э. Пельтри, посвященные вопросу межпланетных сообщений, именно:
1. „Considération stir les résultats d'un allégement indéfini des moteurs“. 1913.
2. „ L'exploration par fusées de la trés haute atmosphére et la possibilité des voyages interlanétaires“. 1928.
3. „Astronautik und Relativitütstheorie“. 1928.
4. „L'Astronautique“. 1930.
Ниже приводится перевод первых трех работ. Что же касается четвертой работы, то она представляет собою капитальный труд, изданный автором в 1930 г. в Париже и заключающий, помимо выше упомянутых работ, еще и ряд новых исследований, снабженных большими номограммами. Издание перевода этой книги хотя и представляется крайне полезным, но недоступно нам по материальным соображениям.
Мы ограничимся здесь лишь приведением оглавления этой книги:
1. История вопроса (стр. 17-24).
2. Резюме работ Годдара и Оберта и Гоманна (25-38).
3. Движение ракеты в пустоте (39-78).
4. Движение ракеты в воздухе (79-108).
5. Расширение горючего газа в дюзе (109-130).
6. Сгорание в камере (131-152).
7. Применение ракет (153-168).
8. Межпланетные путешествия (169-206).
9. Интерес межпланетных изысканий (207-224).
10. Заключение (225-248).
Н. Рынин.
Роберт Эсно-Пельтри (Robert Esnault-Pelterie) (фиг. 1) родился в Париже 8 ноября 1881 года, учился в лицее Janson de Sailly до 1898 года и затем в Сорбонне. В 1902 г. отбывал военную службу. Свои работы в области авиации начал с 1900 года. Сначала его опыты с аэропланом, похожим на аппарат Райта, были неудачны. Тогда он принялся за изыскания наилучших форм крыльев, изучая сопротивление их движению при помощи автомобиля. На основании данных этих опытов он построил в 1907 году свой моноплан, на котором и совершил удачный полет в 1908 году.
 Фиг. 1. Роберт Эсно-Пельтри. |
В 1927 году в Париже была по инициативе инженера Эсно-Пельтри и Андрэ Гирша учреждена ежегодная премия в 5000 франков за наилучшую работу по „ Астронавтике“ (термин, предложенный J. H. Rosny, президентом Гонкурской Академии). Работа должна быть научного характера и относиться, например, к следующим вопросам:
Астрономия и баллистика.
Физика: атомистика, превращение элементов, электро-магнитная межпланетная связь, аккумулирование энергии, применение телескопов с подвижной базой и пр.
Химия: сохранение воздуха для дыхания в замкнутом пространстве, удаление продуктов дыхания, приготовление и сохранение атомного водорода и пр.
Механика: постройка межпланетных кораблей, управление и ориентировка, парашюты и пр.
Металлургия: ультра-легкие сплавы (кальций, глициний, бериллий и пр).
Физиология: влияние ускорения на организм.
В 1930 г. он сделал интересный доклад во Французском Институте о возможности полета в ракете вокруг света в 1 час 26 мин. и из Парижа в Нью-Йорк — в 24 минуты.
В 1930 г. Эсно-Пельтри предпринял поездку в С. А. С. Штаты и сделал по просьбе Американского межпланетного о-ва доклад в Нью-Йорке на тему о межпланетных сообщениях. В этом докладе он предсказывает полет в межпланетное пространство через 25 лет и отмечает необходимость значительных сумм (до 2 миллионов долларов) для осуществления этого полета.
Первая работа Эсно-Пельтри по межпланетным сообщениям была напечатана во французском журнале теоретической и прикладкой физики в 1913 году под заглавием „Соображения о результатах безграничного уменьшения веса моторов “. Вот ее французское название: Esn ault-Pelterie. Considération sur les résultats d'un allégement indéfini des I mot eurs (Journal de physique théorique et appliquée. Cinquième série. Tome III, Année 1913, Mars, pag. 218, Paris).
На русском языке в разное время появлялись заметки о работе Эсно-Пельтри. Нам известны следующие:
Вейгелин, К. Статья в журнале „Природа и Люди“, 1914 г. № 4.
Циолковский, К. Исследование мировых пространств реактивными приборами. Калуга. 1914г. стр. 4-7.
Новая Вечерняя Газета. 1925 г. 20 ноября, № 210. Ленинград. (Заметка).
Заграницей о работе Э. Пельтри упоминают:
Gussalli, L. Si puo già tentare un viaggio dalla terra alia luna? Milano. 1923.
Заметка в газете „Il Secolo“ XIX. Genоva. Martedi. 4 Maggio 1926.
Переходя теперь к статье Э. Пельтри, заметим, что большой, получаемый Пельтри, вес горючего в ракете объясняется не ошибкой в его расчете, как это предполагает К. Циолковский в своих работах, а допущенным Пельтри весьма малым ускорением (11/10 g.) движения ракеты, которое Пельтри считал безопасным для человека и которое, конечно, можно допустить больше.
Идеи, излагаемые в этой статье, возникли у автора, благодаря результатам, которые можно получить уже в настоящее время от применения легких двигателей.
Представляется интересным выяснить, что можно ожидать от этих двигателей, если их вес будет еще значительно меньше. Иначе говоря, какие откроются возможности, если вес двигателя на лошадиную силу будет уменьшаться безгранично. Будет ли тогда прогресс относиться лишь к авиации, или откроются новые горизонты и каковы они будут?
Многие авторы избирали темою своих романов путешествие человека со звезды на звезду. Все обычно считают эту идею невозможной и не думают о реальных физических данных, которые могли бы послужить к разрешению этой задачи.
Выявить эти физические данные, данные некоторых рассуждений, опирающихся на расчеты — вот цель настоящей работы.
I
Первое затруднение, с которым мы встречаемся, это то, что между звездами нет атмосферы, и поэтому для полета в мировом пространстве невозможно применить аэроплан, для которого она необходима, как опора.
Затруднения физиологического порядка будут рассмотрены позже. Теперь же ограничим наши рассуждения разрешением вопроса, позволяют ли наши знания механики допустить возможность существования двигателя, который, исключая какую либо внешнюю опору, мог бы передвигать аппарат.
Хотя это и покажется странным для того, кто не занимался этим вопросом, тем не менее наши познания указывают, что такой двигатель существует уже давно — это ракета. (Пушка Жюль Верна, которая раздавливает пассажиров при отправлении, не может считаться „двигателем для аппарата“).
Часто говорят, что ракета движется благодаря реакции „на воздух“. Первая часть этого утверждения верна, но вторая „на воздух“ — ложна. Ракета движется так же хорошо в пустоте и даже лучше, чем в воздухе.
Для выяснения этого явления предположим, что пулемет установлен на тележке, которая может скользить без трения по рельсам, параллельным оси орудия. Тогда, при каждом выстреле пулемет будет двигаться назад, согласно известного закона механики. Количества движения, с одной стороны приобретенные пулеметом и его тележкой, а с другой стороны пулями, равны и противоположны по знаку. Сопротивление же воздуха лишь уменьшает приобретенные скорости.
В ракете роль пуль играет газ, получающийся от взрыва горючего, газ, который вырывается из ракеты непрерывным потоком.
Пусть будут:
M0 — полная масса аппарата при отправлении.
М1 — его масса во время Р.
dm — масса горючего, которая вырывается из аппарата в элемент времени dt.
Предположим далее, что истечение горючего происходит с постоянной скоростью v по отношению к аппарату, и что расход горючего остается постоянным и равным μ.
Обозначим через V — скорость, приобретенную аппаратом, F — силу реакции, γ — ускорение в момент t.
Расчет показывает, что явление происходит согласно уравнения
Заметим, что если аппарат состоит исключительно из горючего (предположение — чисто абстрактное, но представляющее некоторый интерес), то оно все сгорит через время
Введение этого предельного времени в формулу, которая определяет V в функции от t, дает
* Из (1) имеем 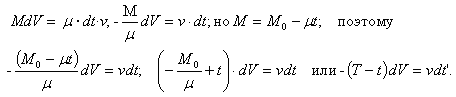 Полагая же, что скорости имеют разные знаки, получим уравнение, приведенное в тексте.
Полагая же, что скорости имеют разные знаки, получим уравнение, приведенное в тексте.
При t = Т — v = — ∞ (в предположении, что v — положительно).
Такой результат не должен нас удивлять, так как сила реакции остается постоянной, тогда как масса уменьшается по мере уменьшения горючего и, в пределе, обращается в нуль. Ускорение же возрастает до бесконечно большой величины. Выражение пройденного пути в функции (t) есть
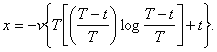
После использования всего горючего, путь будет равен
Таким образом, оставляя в стороне остальные соображения, мы приходим к выводу, что полет в пустоте не представляет невозможного. Однако, мало двигать аппарат, надо им управлять.
В принципе, и здесь не представляется затруднений. Чтобы изменять направление полета, достаточно изменять наклон двигателя, так, чтобы направление силы реакции было наклонным к траектории полета. Если же таковые перемещения двигателя не могут быть сделаны во всех направлениях, то можно применить один или два маленьких двигателя, которые дадут полную управляемость.
Для того, чтобы отправить тело известного веса от центра звезды, необходимо затратить энергию.
Рассмотрим массу М в расстоянии х от центра звезды, радиус которой R. Пусть γ — ускорение силы тяжести на поверхности этой звезды. Для того, чтобы тело прошло еще путь dx, необходимо затратить элемент работы
Откуда работа
Из этого видно, что для удаления определенной массы в бесконечность, необходимо затратить работу
Если же мы будем рассматривать вес тела, как результат всемирного тяготения, то есть сил, действующих между телом и звездою, то, обозначая массу звезды через U, получим
Тогда работа, необходимая для передвижения тела в безконечность, будет равна
Итак, если сообщить телу, отправляющемуся с поверхности Земли, скорость достаточно большую, то это тело улетит в бесконечность.
Для Земли эта скорость равна 11 280 метров в секунду. Иными словами, если снаряд будет отправлен с Земли с такой скоростью, то он никогда не вернется (если сопротивление воздуха не принимать во внимание). Эта критическая скорость равна той, которую приобретает тело, падающее без начальной скорости на планету из бесконечности.
Закон движения такого тела выразится уравнением
Для x = R
Для Земли
Для тела, весом 1 кг и для Земли имеем из уравнения (3)
B = 6 371 103 кг м., что эквивалентно 14 970 калор.
Напомним, что 1 кг смеси кислорода и водорода в соответственной пропорции дает 3860 калорий. 1 кг пороха (fulmicoton + chlorate de potasse) дает 1420 калорий. Таким образом 1 кг смеси водорода с кислородом дает почти 1/4 энергии, необходимой для отправки 1 кг с Земли в бесконечность. Наоборот, 1 кг радия, выделяющего всего 2,9 X 109 калорий, дает энергии в 194 000 раз больше вышеуказанной. При этом, пока, мы не говорим о величине коэффициента полезного действия реактивного двигателя. Если мы будем рассматривать тело, которое удаляется от звезды в ускоренном движении по некоторому закону, то, в момент, когда его скорость будет обратной по знаку и больше той, которую оно имело бы в этой же точке, если бы падало из бесконечности без начальной скорости, то в дальнейшем было бы бесполезно сообщать телу энергию для дальнейшего движения. Его кинетическая энергия обеспечила бы ему бесконечное движение.
Закон движения тела под действием постоянной силы F, бóльшей; его веса, направленной вертикально и центробежно по отношению к звезде, выразится уравнением
Тело приобретает скорость, при которой дальнейший расход энергии будет не нужен, на расстоянии от центра звезды
Раз тело отрывается от Земли под действием силы, равной его весу, т. е. при
Это показывает нам, что тело может совершенно отделиться от звезды при помощи силы тяги, меньшей его веса. Если звезда имеет атмосферу, то тело может лететь сначала, как аэроплан, постепенно поднимаясь и увеличивая свою скорость по мере уменьшения плотности воздуха, пока не достигнет критической скорости.
Определим величину энергии, необходимой для полета тела с Земли на Луну и обратно (фиг. 2).
Полет можно разделить на три периода:
1. Тело движется ускоренно до получения критической скорости, при которой оно освобождается от земного тяготения.
2. Расход энергии (горение) прекратился. Тело движется под влиянием полученной скорости.
3. В некоторой точке оно повертывается дном к Луне, двигатель начинает работать и замедляет скорость, которая должна обратиться в нуль в момент соприкосновения с поверхностью Луны.
Первый период. Прикладываем к телу силу
Критическое расстояние будет
 Фиг. 2. Полет с Земли на Луну. |
В этот момент скорость будет
Время полета в этот период будет
Второй период. Тело продолжает свой полет по инерции и подвергается действию притяжения Земли и Луны. Пусть Р — вес тела на поверхности Земли, Pl — вес его на поверхности Луны, ρ — радиус Луны, D = х+у расстояние между Землей и Луной. Расчет дает
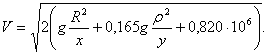
В месте, где притяжения Земли и Луны сравниваются, скорость будет
Это наименьшая скорость в пути.
При подходе к поверхности Луны она будет равна
Скорость же свободного падения из бесконечности на Луну будет
Время прохождения пути во второй период можно определить, пренебрегая силой притяжения Луны, которая оказывает ничтожное влияние. Это время будет равно тому, которое понадобится телу для полета от Луны до точки, где прекратилось действие двигателя
Третий период. Теперь необходимо затормозить движение, повернув аппарат и пустив в ход двигатель.
Каков же будет закон этого замедленного движения? Мы его можем уподобить таковому же относительно Земли, учитывая лишь, что притяжение Луны гораздо слабее.
Так как нам нет нужды в большой точности, мы ограничим ускорение, которое должен побороть двигатель, величиной равной половине ускорения на поверхности Луны, и предположим, что движение происходит замедленно под влиянием этого фиктивного ускорения.
Находим, что поворот аппарата необходимо сделать в расстоянии от поверхности Луны
Время периода торможения будет
Итак имеем приблизительно время полета:
| 1 период — 0 ч. 24 м. 9 с. 2 3 Итого ок. 48 ч. 58 м. — |
Для обратного полета потребуется почти такое же время и в обратном порядке.
Следует заметить, что двигатель будет работать лишь в течение 28 минут при полете туда, и столько же при полете обратно, если только не утилизировать при спуске тормозящее действие земной атмосферы.
Определим теперь действительную минимальную мощность, необходимую для осуществления полета, учитывая и отдачу двигателя.
Пусть вес аппарата — 1000 кг, из которого 300 кг приходится на топливо.
Если (учитывая, что при спуске на Землю тормозить будет только атмосфера) двигатель будет работать лишь 27 + 3,5 м или с запасом
Смесь Н2+О содержит энергии в 133 раза меньше, а другие, наиболее энергичные вещества — в 360 раз меньше.
Наоборот, 1 кг радия содержит энергии в 5670 раз больше.
Мощность двигателя, необходимого для нашего аппарата, будет
Далее необходимо заметить, что отдача реактивного двигателя довольно плохая. Действительно, чтобы удалить массу в 1 кг от Земли в бесконечность, необходимо ей сообщить работу в 6371103 кг м. Мы же ее определили для двигателя в 217,2·106. Таким образом, отдача будет
Кроме того, для сообщения газу скорости извержения 65 300 м/с в пустоте, необходимо нагреть его до невероятной температуры 2,525·106.
При полете же в воздухе, условия будут еще хуже, так как кроме увеличения этой температуры потребуется еще и большее давление.
IV
Предположим, что двигатель, после достижения аппаратом критической скорости, продолжает работать и прекращает работу, когда скорость будет равна 10 км/с. Тогда время, необходимое для достижения наиболее близких к Земле планет, в момент их наибольшего приближения к ней, равно:
Следует заметить, что расход энергии для осуществления этих перелетов не будет чрезмерно превышать того минимума, который необходим для преодоления силы земного тяготения. Действительно, раз аппарат отлетел от Земли на достаточно большое расстояние, он продолжает свой путь по инерции, и земное притяжение замедляет полет его весьма мало.
Таким образом, главная трудность заключается в преодолении силы земного тяготения, если же эта сила преодолена, то достичь планет, как далеких, так и близких, не составит особого затруднения. При этом, конечно, необходимо пассажирам обеспечить возможность безопасного для жизни пребывания внутри герметически закрытого аппарата, что мы рассмотрим позже.
В предыдущих параграфах мы предполагали лишь теоретическую возможность полета аппарата между Землей и Луной. Это представляет собою задачу чистой механики, которая не касается вопроса, может ли в действительности человек когда либо покинуть нашу планету и исследовать другие.
Это приводит нас к вопросу об исследовании физиологических условий, которые необходимо выполнить для осуществления подобного полета.
Успехи, достигнутые при подводном плавании, указывают на возможность очищать воздух в течение известного времени.
Вопрос же о температуре требует особого рассмотрения. Обычно полагают, что температура межпланетного пространства есть абсолютный 0°. Автор, однако, думает, что это не так.
Температура имеет место лишь для тел материальных, и в пустоте ее нет (это доказывают вазы Dewar'a). Если приток тепла к аппарату в единицу времени меньше расхода его, то температура его понижается; если же приток больше расхода, то, она повышается. Можно построить аппарат так, что половина его поверхности будет из полированного металла и нетеплопроводного изнутри. Другая же половина может быть сделана, например, из оксидированной меди, образующей черную поверхность.
Если полированная поверхность будет обращена к солнцу, то температура аппарата понизится; при обратном положении — она повысится.
Все упомянутые затруднения указывают, что задача в принципе разрешима. Однако, следует обратить внимание еще на одно затруднение, которое усложняет практическое решение задачи.
Действительно, в рассмотренном нами примере полета с Земли на Луну мы предполагали ускорение
Если организм не приспособится к подобной перемене, то, при отсутствии поля тяготения, следует создать таковое искусственно в степени, хотя бы равной земному, и тогда путешественники будут сохранять свой земной вес, где бы они ни находились в мировом пространстве.
Однако, такое приспособление потребует большого расхода энергии и еще более затруднит решение и без того трудной задачи.
Если мы обратимся к формуле, выражающей закон движения тела под действием постоянной силы с момента отправления от Земли, и если мы предположим, что, до получения максимальной скорости между Землей и Луной, мы утилизируем ускорение равное 11/10 земного, и, что все другие манервы происходят с ускорением равным земному, а также, что действием лунного притяжения, ввиду его незначительности, можно пренебречь, то расчет покажет, что аппарат должен повернуться на расстоянии от центра Земли равном 29.5 земных радиусов.
В этот момент скорость будет 61 700 м/с. После этого повернутый аппарат будет тормозиться силой, равной его земному весу.
Время необходимое для достижения Луны будет равно
Однако в этом случае, затрата работы для полета аппарата весом в 1000 кг, из которых 300 кг приходится на горючее, будет 67,2·106 калорий на 1 кг топлива, т. е. в 131 раз больше, чем в первом случае.
Динамит слабее в 47 300 раз, но радий еще в 433 раза сильнее.
Необходимая мощность будет
Если этот способ движения мы применим для полета на ближайшие планеты, то получим следующие наибольшие скорости и продолжительности пути:
| Скорость | Продолжительность | |
для Венеры........... „ Марса............ | 643 км/с 883 ,, | 35 ч. 04 м. 49 „ 20 „ |
Хотя указанные скорости и представляются невероятными, однако, существуют небесные тела, которые достигают скоростей того же порядка, например, комета Галлея.
Лишь молекулярные силы и энергия частиц дадут нам возможности для упомянутых полетов.
Если допустим, что в аппарате весом 1000 кг мы в том же весе имеем 400 кг радия, что мы умеем извлекать из него энергию в любое время по нашему желанию, то этого количества нам хватит с запасом для полета на Венеру и обратно, и в обрез — для полета на Марс и обратно (с постоянным ускорением).
Предлагаемый перевод является развитием работы Эсно-Пельтри, сделанной им в 1913 году.
В настоящей работе автор дает ряд оригинальных выводов и гипотез, которых у других ученых, занимающихся проблемой межпланетных сообщений, мало или совсем не затронут. К этим вопросам относятся:
1. Представление движения аппарата в пустоте без тяги при помощи, так называемых, критических кривых и изучение экономики движения, т. е. случая расхода minimum'a горючего.
2. Анализ наивыгоднейшей формы ракеты. Автор разбирает три случая ракет: цилиндрическую, коническую и экспотенциальную, т. е. ракету, движущуюся с постоянной тягой, и отдает предпочтение последней, в особенности для полета людей.
3. Автор советует при пассажирских полетах допускать ускорения, мало отличающиеся от земного (1.1 - 2g), ввиду возможной опасности больших ускорений для организма.
4. Особенно обстоятельно им исследован вопрос о нагревании аппарата при проходе его в атмосфере, а также освещен вопрос о температурах аппарата, которые он получит близ Земли, Венеры, Марса и Меркурия на солнечной и на теневой сторонах.
5. В вопросе о горючем автор допускает возможность, при имеющихся сортах его, посылки ракеты в верхние слои атмосферы, но считает, что полет на планеты или на Луну возможен лишь тогда, когда человек овладеет внутриатомной энергией. Пока же желательно использовать атомный водород, свойства которого еще мало изучены.
6. Признавая теорию С. Аррениуса („панспермию") переноса зародышей с планеты на планету несостоятельной, автор выдвигает свою гипотезу о появлении жизни на планетах, считая ее как один из видов физико-химических явлений, продолжающихся все время и находящихся в постепенной эволюции форм от простейших к более сложным.
В заключение автор призывает к работе по достижению заманчивой проблемы - межпланетных сообщений, путем исследования ряда частных вопросов, чтобы быть готовыми к моменту, когда физики дадут человечеству возможность пользоваться внутриатомной энергией.
Н. Рынин.
Мечта о полете с земли в безграничные звездные пространстве к так же стара, как старо само человечество. Роберт Эсно-Пельтри в ниже следующем своем докладе подходит с научной стороны к задаче, которая в течение многих веков трактовалась разными авторами преимущественнс с фантастической точки зрения. Греческий писатель Лукиан и французский писатель XVII века Сирано-де-Бержерак предлагали самые фантастические способы преодоления земного тяготения. Кто не помнит более близкие к нашему времени проекты снаряда Жюль-Верна и курьезный аппарат Уэльса, в котором достигли Луны первые люди и в котором наружная оболочка обладала таинственным свойством образовывать экран против сил тяготения. Говоря об этой области фантазии уместно здесь вспомнить мало известного романиста Ахилла Эйрода, который в 1865 году предложил для полета с земли род ракеты или реактивного двигателя.
Научное исследование такого двигателя может быть отнесено ко времени лишь 20 лет тому назад, когда Роберт Эсно-Пельтри первый* занялся этой темой в 1907 году, но опубликовал свои идеи в 1912 году, - дата его доклада во Французском Физическом о-ве. Хотя эта увлекательная проблема с тех пор изучалась и другими лицами, среди которых Р. Эсно-Пельтри называет доктора Бинга и американского профессора Годдара, однако можно сказать, что сам автор доклада первый охватил вопрос во всей его широте; он предпринял и широко развил изучение вопроса с научной точки зрения о полете живых существ в таинственные межпланетные пространства.
* Здесь автор ошибается, так как первым, давшим теорию как полета ракеты вообще, так и движения ее в межпланетном пространстве, был русский ученый К. Э. Циолковский (1903 год).
Конечно, проблема еще далека от окончательного разрешения, однако, первый этап уже пройден и ясно показано, какие препятствия еще следует преодолеть в устройстве ракеты, чтобы она могла унести нас к светилам.
Может быть уже близок день, когда человечество будет иметь в своем распоряжении внутри-атомную энергию и тогда осуществятся идеи, столь смело и талантливо высказанные Р. Эсно-Пельтри.
Последний имеет уже ряд прекрасных научных работ разного рода. В особенности в авиации он был пионером и высказывал идеи, часто значительно опережавшие свой век, что указывало на проницательность и интуицию их автора.
Большинство знает его, как изобретателя „manche a balais", т. е. рычага управления, принятого в авиации. Он является автором и ряда других замечательных работ, относящихся к авиации, автомобилизму и, вообще, к механике.
Он был первым, предложившим прямой метод к изучению законов аэродинамики (1905 г.).
В 1906 г. он построил моторный моноплан, что было новизной в это время.
Он предложил испытывать прочность самолетов нагрузкой песком.
Он установил новый метод измерения твердости металлов.
Ниже помещаемый доклад был сделан на общем годовом собрании Астрономического о-ва в 1927 году. Помимо формул и расчетов, представляющих большой интерес, автор раскрывает перед читателем ряд возможностей, окрыляющих человеческое воображение.
С надеждой на осуществление будущей эпохи межпланетных путешествий можно сказать вместе с поэтом:
Si nous pouvions franchir ces solitudes mornes; Si nous pouvions passer les bleus septentrions; Si nous pouvions atteindre au fond des cieux sans bornes, Jusquà ce qu'a la fin, éperdus, nous voyions, Gomme un navire en mer croît, monte et semble éclore, Cette petite étoile, alome de phosphore, Devenir par degrès un monstre de rayons. V. Hugo. |
Генерал Феррье.
Член Института.
Приводим перевод этих стихов, сделанный Т. Рыниной.
Когда-б преодолеть безбрежные пустыни, Медведицы лазурные светила миновать, И безграничные постичь небес глубины, Тогда смогли-б мы, пораженные, там увидать: Подобно кораблю, плывущему в безбрежном море; Так эта звездочка, фосфористый атом, растет в космическом просторе, Что-б, наконец, сияющим светилом мощно стать. В. Гюго. |
В октябре 1927 года мой друг Андрэ Гирш указал мне на ряд работ относящихся к интересующей меня теме. Я старался безуспешно достать их в Вене, где мне пришлось быть позднее. Там я узнал о появлении еще работы Лоренца (Данциг), опубликованной 7 мая 1927 года в журнале Zeitschrift des Vereins deutscher Ingenieure. В этой, весьма серьезной работе, хотя и несколько краткой, была указана библиография, кроме книги Годдара, уже мне известной, еще и новых, неизвестных мне книг:
1925. Н. Oberth „Die Rakete zu den Planeten-Räumen".
1925. W. Hohmann „Die Erreichbarkeit der Himmelskörper".
1925. M. Valier. „Der Vorstoss in den Weltenraum".
Первые две работы мне удалось получить 14 января 1928 года, при чем книгу Оберта я достал в издании 1923 г., а не 1925 года. В работе Гоманна я с удивлением нашел ряд вопросов, составлявших предмет моего изучения, а в некоторых частях он в своей работе шел еще дальше, как например в вопросе о торможении полета в атмосфере, когда он говорит о последовательных облетах земли по эллипсам. Однако, при этом автор рассматривает проходы атмосферы на высоте 75 км со скоростью 11 км/с, не отдавая себе отчета о нагревании аппарата, которое будет настолько значительным, что сделает его неуправляемым.
Что касается отношения начальной и конечной масс аппарата, то здесь результаты Гоманна сходятся с моими, что весьма важно. Поразительно, что он, как и я, ведет свои расчеты до скорости извержения газов 10 000 м/с. Однако, он допускает ускорение 20 g , что дает выгоду не очень большую по сравнению с 10 g. Эта работа заслуживает серьезного изучения, а не краткого упоминания; я очень сожалею, что не познакомился с нею раньше.
В работе Оберта, также обстоятельной и заслуживающей внимания, разбираются вопросы эффекта ускорения и даже даются чертежи ракет.
Приступая к своей работе, я не мог не упомянуть об этих двух работах и не отдать им должного уважения.
При этом я должен просить извинения, если я пропустил другие труды по незнанию, так как не легко собрать библиографию по этому вопросу, и я тогда еще не получил вышеупомянутой книги Вальера.
Г-н президент, м. государыни и м. государи.*
* Доклад на общем собрании Французского Астрономического о-ва 8 июня 1927 года.
Наш президент, генерал Феррье, по предложению нашего коллеги Андрэ Гирша обратился недавно ко мне с предложением сделать более подробный доклад перед членами о-ва на тему, сообщенную мною 15 ноября 1912 года во французском Физическом о-ве. При этом я добавляю обзор работ, с которыми я ознакомился после упомянутой даты.
Когда, 15 лет тому назад, я хотел сделать доклад о возможностях и трудностях, относящихся к межпланетным путешествиям, в эпоху, когда зародилась авиация и окрыляла надежды, мне казалось более осторожным по многим, может быть и неблагоразумным соображениям, скрыть истинную цель моей работы под названием: „Соображения о результатах беспредельного уменьшения веса моторов".
Ныне я имею возможность опубликовать мои идеи под их истинным названием.
Объем моего прежнего доклада был настолько сокращен секретарем Физического о-ва, что моя мысль часто могла быть едва понята читателем, и это заставляет меня теперь высказаться подробнее, чем это было возможно ранее. Мои идеи на эту тему возникли гораздо раньше упомянутого времени. Давно уже я был поражен той ошибкой, которую допустил Жюль-Верн в своем романе „С Земли на Луну", в котором он описывает путешественников, заключенных в снаряде, выбрасываемом из пушки, длиною 300 метров. При этом, чтобы избежать раздавливания силами инерции при взлете, он помещает у основания снаряда настил высотою в 2 метра, который и должен ломаться. В действительности же эффект действия этого настила был эквивалентен лишь удлинению пушки с 300 до 302 метров, т. е. почти не изменил условие действия сил инерции и опасности для путешественников быть сплющенными.
Отсюда я заключил о необходимости дать разбег снаряду в несколько километров, что привело к применению ракеты.
Я сам не мог бы установить даты появления этой моей идеи, если бы, к счастью, на нее не было ссылки в старой книге капитана Фербера „От холма к холму, от города к городу, от континента к континенту", где он, на стр. 161, говорит:
„Чтобы лететь выше, а этого человек желает, необходимо пользоваться разными способами. Наиболее применим принцип ракеты, летящей под влиянием реакции. Человек будет в ней закрыт герметически, и будет дышать искусственно вырабатываемым воздухом. По существу это будет уже не летательная машина, а управляемый снаряд. Осуществление этой идеи не представляется невероятным, пока солнце снабжает нашу планету запасами энергии. Уменьшение теплоты на земном шаре может быть послужит толчком к новому прогрессу, так как тогда жизнь на земле будет под угрозой. Перед человечеством встанет грозная дилемма: или вернуться к эпохе предков и идти по пути регресса, или идти к новым завоеваниям человеческого гения.
Это предстоит сделать будущим более могущественным и более развитым людям.
Некоторые из них покинут тогда нашу негостеприимную планету, и тогда наступит торжество аппарата легче воздуха, который зародился на наших глазах".*
* „Мы упомянем о людях, которые разделяют эту идею, именно о Уэльсе, Эсно-Пельтри, Арчдеаконе, Квинтоне и о других философах". (Примечание автора).
Примечание к этой книге обозначено Фербером датой 26 июля 1908 г. Таким образом мои идеи фиксируются датой первой половины 1908 года. Я должен заметить, что подобные же идеи высказывал в то же время другой человек, доктор Андрэ Бинг, которого я раньше не знал, и который, после доклада моего в 1912 году, прислал мне свой патент за № 236377 (Бельгия) от 10 июня 1911 года на тему: „Аппарат для исследования верхних слоев атмосферы", и сообщил, что он, несколько лет раньше, беседовал по этому вопросу с моим коллегой по Обществу фрацузских ученых и изобретателей, Эдуардом Белин, изобретателем передачи изображений на расстоянии.
Наконец, в 1912 - 1913 г. американский профессор Роберт Годдар в Принцтонском университете (С. А. С. Ш.) сделал ряд теоретических, подсчетов, а позднее, в 1915 - 1916 г. в Университете Кларка (Ворчестер, Массачузец) произвел ряд опытов с ракетами, предназначенными для исследования высоких слоев атмосферы, следуя идее, высказанной столь поразительно доктором Андрэ Бингом. Профессор даже пришел к заключению, что возможно послать на Луну снаряд с зарядом магнезийного пороха, вспышки которого можно увидеть с земли в телескоп.
При чтении привилегии доктора Бинга получается впечатление, что автор, вероятно, не произвел подсчетов, подтверждающих изобретение, однако, как он мне писал в 1913 году, и как это напрашивается само собою, он просто хотел этим патентом закрепить за собою свой приоритет. При чтении патента можно вывести, хотя и не совсем ясное, заключение, что возможно достичь почти безграничной высоты, при помощи взрыва последовательных ракет, при чем сгоревшие последовательно отпадают, что и составляет главный принцип профессора Годдара, когда он рассчитывает послать снаряд вне атмосферы при шестисоткратном начальном весе против полезного груза. Иными словами, например, для посылки в межпланетное пространство или на Луну (что практически то же самое) груза в 1 кг, необходимо иметь начальный вес снаряда в 600 кг.
Результаты, полученные профессором Годдаром и мною, кажутся на первый взгляд, противоречивыми, так как первый считает возможным посылку снаряда в мировое пространство, я же полагаю пока невозможным послать туда аппарат, способный преодолеть земное притяжение, пока не найден будет более мощный источник энергии вроде радия, какового пока в нашем распоряжении нет.
Однако, это противоречие лишь кажущееся и происходит от того, что Годдар и я изучаем вопрос исходя из разных точек зрения.
Он хочет просто послать на Луну снаряд с порохом и определить момент взрыва на Луне в телескоп. Я же исследую вопрос пересылки живых существ со светила на светило и возвращение их на Землю. Я прекрасно видел возможность посылки небольшой доли снаряда на известное расстояние, как о том свидетельствует формула моего доклада 1912 года, равно как и фраза, следующая за нею вверху страницы 5 (§ II), но при этом отдавал себе отчет, что для этого потребуется громадная начальная масса снаряда. Я считал подобный способ не применимым в случае полета живых существ. В последнем случае, как я докажу ниже, начальная масса должна быть не в 600 раз, а в несколько тысяч раз больше конечной массы, если только желать, чтобы путешественники не были раздавлены при взлете, как это должно было бы быть с героями Жюль-Верна при вылете их из пушки, да еще и по другим, ниже приводимым, соображениям.
Вот каковы, в общих чертах, выводы из моего доклада 1912 года, которые я счел необходимым здесь привести, чтобы у читателя не возникло каких-либо недоразумений. Настоящий мой доклад заключает в себе следующее:
Глава I. Изучение полета ракеты в пустоте; уравнение движения; наиболее экономичная форма; ракеты цилиндрические, конические и экспотенциальные; высоты и скорости либерации (начало свободного полета) коэффициент утилизации.
Глава II. Изучение полета ракеты в воздухе; уравнение движения; уравнение сопротивления воздуха; баллистический коэффициент; наиболее экономичная форма; при известных условиях, сопротивление воздуха не меняет значительно условий, полученных для полета в пустоте; температура сжатого воздуха перед ракетой; допускаемые ускорения.
Глава III. Применение ракет для исследования высших слоев атмосферы и для межпланетных путешествий; стрельба в Луну; полет вокруг Луны; условия, зависящие от скорости извержения; на какие скорости извержения можно расчитывать; возможности осуществления.
Глава IV. Условия, необходимые для перевозки живых существ; межпланетный корабль; условия жизни в нем; физиологический эффект отсутствия ускорения; управляемость; условия ее осуществления; продолжительность и скорость путешествия на Венеру и на Марс.
Глава V. Какой научный интерес представляет посещение других миров? Что мы можем там найти? Обитаемы ли они?
Изучение этой, более простой, задачи является весьма важным для дальнейшего исследования общей задачи с учетом сопротивления воздуха.
Взлет ракеты разделяется на 2 периода: первый или период горения с ускорением в полете и второй - после сгорания всего горючего, когда ракета не имеет реакции, но летит по своей траектории под влиянием полученной скорости.
Рассмотрим пока исключительно прямолинейную зенитную траекторию и введем следующие обозначения:
V - скорость ракеты в данный момент.
v - абсолютная скорость извержения газов.
m - наличная масса горючего (для времени t0, т = m0).
р - конечная масса ракеты.
М = m+р - полная масса ракеты в данный момент.
F - сила реакции в данный момент.
Г - ускорение.
dm - элемент массы, извергаемой в данный элемент времени dt.
у - высота в данный момент.
G - ускорение силы тяжести на данной высоте (на уровне моря G = g.
R - сила сопротивления воздуха.
Примечание. Я считаю положительными длины, силы и ускорения направленные вверх, равно как и V. Величины же v, G и R будут положительными по существу (par essence).
Реакция в дюзе. Предположим, что в дюзе установился постоянный режим извергающихся газов (фиг. 3). В момент t в ней содержится
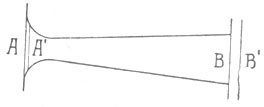 Фиг. 3. |
Часть, заключенная между плоскостями А1 и В является общей в обоих случаях.
Часть между В и В1 есть масса - dm, изверженная во время dt и она равна массе А и А1. Эта последняя имеет весьма малую скорость и ее количество движения будет бесконечно малым и второго порядка. Наоборот, первая приобретает скорость извержения, и количество движения ее - vdm будет первого порядка.
Так как другие части газа сохраняют свои скорости, то теорема проекции количества движений дает
*- dM представляет часть полной массы М ракеты, выброшенную за время dt; конечно dM= dm < 0.
Так как dm и dM - отрицательны, то Г будет положительным.Для того, чтобы представить формулы более наглядно, я рассмотрю абсолютные значения G и R и напишу общее уравнение движения
Однако, имея в виду пока движение в пустоте, получим
Можно начертить диаграмму, изображающую движение, откладывая по абсциссам V, а по ординатам у, ограничиваясь случаем положительных у и V.
Заметим, что
Поэтому уравнение (5) можно написать в виде
Критическая кривая. Под названием критической кривой я понимаю кривую, изображающую движение снаряда без извержения газов (без тяги.) Термин этот объясняется тем, что для достижения данной высоты y нет надобности развивать ускорение ракеты до этой высоты, а достаточно развивать его лишь до некоторой, меньшей высоты, соответствующей какой то точке критической кривой, проходящей через точк; высоты У; далее же полет будет происходить по инерции.
Уравнение критической кривой получается из (4 bis), полагая в нем Г = 0, что, в связи с (7) дает
Для малых высот (из дальнейшего будет видно, каких)
Интегрируя, получаем
Уравнение (10) можно представить в виде
Уравнение критической кривой в пустоте, отнесенное к переменной η, будет
Для получения значения η(V,y), достаточно интегрировать (12).
Обозначим через а - радиус Земли; тогда
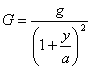 .............(14)
.............(14)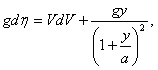 .............(14 bis)
.............(14 bis)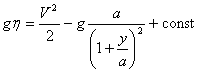 .............(15)
.............(15)Полагая η = 0 для y = V= 0, имеем
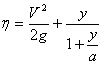 .............(16)
.............(16)Если у достаточно мало сравнительно с а, то
Наиболее экономическая кривая. Предполагая, что среда не оказывает сопротивления полету, получим, что для подъема даже на несколько сот километров придется затратить много энергии, и поэтому главной задачей является достичь minimum'a массы топлива, необходимого для подъема данной конечной массы р на данную высоту.
 Фиг. 4. |
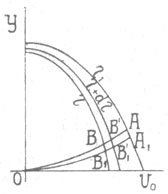
Вычертим критическую кривую (фиг. 4) V0AY(η,),) проходящую через конечную высоту, и пусть ОBА будет некоторая кривая, соответствующая периоду горения и тяге.
Проинтегрируем уравнение 9
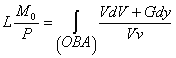 .............(17)
.............(17)Так как
Уравнение (9) и (12) нам дают
Дифференциальный элемент второй части (17) можно написать, согласно (12), в виде
Проводим кривую ОВ1 В1 A1, расположенную ниже кривой ОВВ1А и возьмем на ней элемент В1В1, который, вместе с ВВ1 соответствует одному и тому же значению dη. Из этих двух элементов наименьшим будет тот, для которого произведение Vv будет большим, причем независимо от того, какая пара элементов будет выбрана.
Это заставляет нас выбрать наибольшее значение v, определяемое физико-химическими свойствами взрывчатых веществ, которыми мы можем располагать. И если мы таковое вещество выбрали, то v тогда можно считать постоянным.
Благодаря форме кривых η, всегда из двух элементов ВВ1 и В1В11, второй будет соответствовать большему V, и это относится ко всем элементам кривых ОВА и ОВ1А1. Таким образом вторая кривая является выгоднее первой. Переходя к пределу, видим, что наиболее экономичной кривой горючего будет часть OV0 оси V, и для нее отношение M0/P будет minimum.
При этом период горения должен быть мгновенным, ускорение - бесконечно большим, и снаряд имеет подъем dy = 0, при чем формула (17) приводится к виду
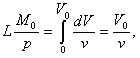 ............. (21)
............. (21)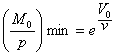 .............(22)
.............(22)Если теперь мы рассмотрим формулу (16), приложив ее последовательно к точкам V0 и Y кривой η1 = const., то получим
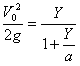 ............. (23)
............. (23)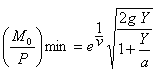 .............(23 bis)
.............(23 bis)Если Y мало по сравнению с земным радиусом а, то
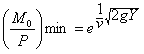 .............(23 ter)
.............(23 ter)При наиболее благоприятных теоретических условиях, и допуская скорость извержения 2000 м/с, для преодоления силы земного притяжения конечной массой в 1 кг. потребуется начальная масса в 269 кг., т. е. величина значительно меньше полученной Годдаром и для случая воздуха, а не пустоты. Если же взять v = 2500 м/с, то эта величина снизится до 88 кг.
Однако, не следует упускать из вида, что эти числа соответствуют исключительно абстрактным условиям, и что, если бы пришлось сообщить конечной массе мгновенное и бесконечно большое ускорение, то эту массу пришлось бы сплющить в пластинку без толщины, так, чтобы количество ее на единицу площади равнялось нулю; но тогда ее площадь была бы бесконечно большой и ее границы потеряли бы физический смысл; наконец, при полете в атмосфере выступило бы важное условие об уменьшении сечения аппарата.
Минимальное сечение. Вышеприведенная теория указывает, для площади извержения на единицу массы, верхний бесконечно большой предел. Желательно исследовать вопрос, как это сечение, отнесенное к единице массы, может быть по желанию уменьшено или безгранично, или доведено до некоторого нижнего предела и какого, и опять таки для случая полета в пустоте и с теоретической точки зрения, что пригодится нам позднее при изучении полета в воздухе.
Определение площади извержения. При расширении совершенного газа в дюзе получается скорость извержения, определяемая уравнением
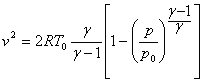 .............(24)
.............(24)Следует заметить, что давление у выхода из дюзы не определяется давлением в средине ее, где газ расширяется, а скорее определяется отношением сечения устья к сечению горла, учитывая начальные температуру и давление; при этом я здесь не излагаю всю теорию сопл Лаваля. Отсюда следует, что для случая пустоты, чтобы быть логичным, необходимо принять площадь устья бесконечно большой, что приводит нас, как и ранее, к абсурду.
Для выхода из этого затруднения достаточно применить ракету с очень высоким давлением (1000 и даже 2000 кг. на см2), причем, при очень большой степени расширения (100 или 200), газ имел бы при выходе еще достаточно большое давление (10 или 20 кг. на см2), преобразуя в то же время в живую силу большую часть своей энергии, теоретически 74% при степени расширения в 100 и практически, как в опытах Годдара в 64% при степени расширения не указанной.
Отсюда можно заключить, что сечение устья дюзы должно быть возможно большим, т. е. равным миделю снаряда; при очень высоких давлениях, под которыми он будет функционировать, этот мидель позволит достичь степени расширения, достаточной для преобразования большей части энергии в живую силу.
Эти рассуждения позволяют нам вывести следующие упрощенные теоретические заключения о ракетах: сечение устья дюзы является сечением извержения газов и равняется сечению миделя снаряда; через это устье газ извергается в своей конечной стадии расширения со скоростью v. Если предположить, что перед дюзой находится резервуар с горючим, то расход последнего пропорционален расходу массы изверженного газа.
Таким образом мы заменяем действительную ракету теоретической, состоящей из твердого горючего, формы поверхности вращения, имеющей в данный момент скорость данного направления, служащей осью этой поверхности, и ограниченного сзади плоскостью нормальной к этой скорости. Эта плоская поверхность является поверхностью горения и от нее извергаются назад газы со скоростью v. Эта поверхность, по мере расхода горючего, движется в массу его с такою скоростью, что расход газа постоянно соответствует скорости извержения v через устье.
Так как это, чисто теоретическое, упрощение в действительности не совместимо с условием хорошей утилизации энергии, которое требует применение дюзы, то необходимо показать, что оно все же законно и допустимо, так как в дальнейшем оно сильно упрощает все рассуждения. Когда будет идти речь о цилиндрической ракете, то это будет означать, что сечение извержения остается постоянным; если ракета будет конической, то сечение извержения ее остается пропорциональным ⅔ остающейся массы; наконец, если речь будет идти о ракете с постоянной тягой, то в этом случае сечение извержения будет оставаться пропорциональным остающейся массе.
Итак, сечение извержения теперь определено. Объем газа, извергаемого за элемент времени dt будет равен
Пусть плотность его, тогда извергнутая масса будет
Тяга (реакция) будет
Здесь ρ и v определяются физическими свойствами горючего. Поэтому мы можем по произволу располагать лишь значением ![]() .
.
При отправлении с Земли имеем
Правая часть этого неравенства выражает minimum сечения извержения для подъема начальной массы М0.
Пусть мы имеем некоторый аппарат А формы поверхности вращения вокруг направления скорости, и задан меридиан этой формы. Сравним его с цилиндрическим аппаратом С с теми же начальной и конечной массами причем сечение извержения его постоянно равно наиболее сильному сечению извержения А. Тогда будем иметь всегда
Это имеет место для одних и тех же случайных высот. Скорость расхода горючего, и, вследствии этого, облегчение А, будет всегда меньше или, в крайнем случае, равными таковым же С; по истечении одного и того же времени, оставшаяся масса А будет всегда больше, или, в крайнем случае, равной оставшейся массе С. Если, однако, как это бывает, принять за независимую переменную не время, а высоту у, то это условие уже не является обязательным и здесь могут представиться следующие два случая.
1°. При одинаковой высоте подъема оставшаяся масса А всегда больше таковой же С.
При одном и том же случайном интервале высоты dy имеем следующие элементарные работы
Так как эти работы затрачиваются для определения сил тяготения и для сообщения кинетических энергий, то для одинаковых высот будем иметь
Но так как в этом случае всегда
Суммируя от 0 до некоторого у и извлекая квадратный корень, получим VA≤VC.............(38)
Но ракета А имеет по крайней мере хотя бы в одном месте сечение меньше, чем сечение с другой ракеты иначе обе ракеты были бы идентичны; поэтому всегда
Это последнее неравенство приложимо и к случаю, когда, на известной высоте, одна из ракет израсходовала все свое горючее; согласно предыдущему это будет иметь место для цилиндрической ракеты на высоте, где другая еще имеет запас горючего.
Нанесем кривые горючих (фиг. 5)
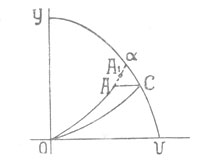 Фиг. 5. |
Предположим, что этот запас будет израсходован мгновенно в тот момент, когда аппарат А достигнет высоты соответствующей концу горения С. Тогда его кривая стала бы параллельной оси У, но она не могла бы достичь предельной точки кривой С. Действительно, если бы это случилось, то это могло бы быть лишь за счет расхода топлива большего, чем у С, потому что, на основании предыдущих рассуждений, кривая ОАС соответствует большему расходу горючего, чем ОС.
Далее, мгновенный расход остатка горючего А потребует бесконечно большого сечения и кривая А не может идти изгибаясь по АС; она будет продолжать подниматься, например, до точки А, где ей еще меньше оснований изогнуться и идти в С.
2°. Если ракета А будет долго оставаться на высотах, мало отличающихся друг от друга, то может случиться, что, по израсходовании части горючего, она достигнет высоты большей с меньшим остатком горючего, чем ракета цилиндрическая на тех же высотах.
Предположим, что на каждой высоте, где ракета А стремится сделаться легче С, мы будем мешать этому, препятствуя соответственно расходу ее активной массы так, чтобы на всех высотах сохранялось неравенство
Тогда останется в силе предыдущий ход доказательств, хотя эффект действия ракеты С в конце концов и уменьшится.
Заключение. Назовем коэффициентом утилизации ракеты отношение
Тогда мы можем сказать, что цилиндрическая ракета имеет коэффициент утилизации лучший по сравнению с другими ракетами того же максимального сечения; иными словами, она может поднять на ту же высоту большую конечную массу или ту же конечную массу поднять на большую высоту.
Рассмотрим цилиндрическую ракету, для которой
Тогда
Аппарат взлетит и будет подниматься по известному закону. Предположим теперь, что мы затрудним взлет, прибавив к ней взрывчатый цилиндр того же сечения и массы m1 так что
В тот момент, когда эта масса m1 совершенно сгорит и начнет работать основной аппарат, он будет уже обладать некоторой скоростью и достигнет некоторой высоты; поэтому при работе горючего основного аппарата он достигнет большей скорости и высоты, чем ранее.
Таким образом мы или увеличим конечную высоту, или увеличим конечную массу, если прекратим горение в момент, где соответствующая точка второго аппарата достигнет критической кривой основного.
Заключение. Среди всех цилиндрических ракет одинакового сечения, та, у которой начальная масса будет наибольшей, поднимет выше одну и ту же конечную массу, или на одну и ту же высоту поднимет большую массу, но за счет уменьшения коэффициента утилизации
Критическая кривая. Мы уже видели, что для того чтобы достичь данной высоты H, достаточно производить горение до момента, когда точка (V, у) придет на критическую кривую с пределом V=0 и у = Н.
Уравнение этой кривой получаем из (16) и на основании двух выше приведенных случаев
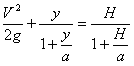 .............(42)
.............(42)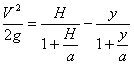 .............(43)
.............(43)При H =∞ имеем
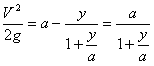 .............(44)
.............(44)Это есть уравнение кривой движения (либерации) снаряда в пустоте.
Прежде чем разрешать полностью теоретическую задачу с учетом сопротивления воздуха, интересно выяснить, каковы могут быть границы теоретических возможностей, применимых к действительной их реализации.
Для упрощения понятий я буду считать ракеты в действительности цилиндрическими, коническими или иной, ранее определенной формы. Сечения извержения обозначим через S, длину в момент t через l. Горючее однородного состава плотностью ρ и скорость сгорания его v1 имеем
Кроме того, в каждый момент
Интегрируя (45), получим
При конечной начальной длине l0 ракеты полное время горения будет
Уравнение движения дает
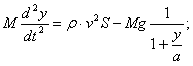 .............(51)
.............(51)Интегрируя (46), получаем
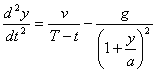 .............(55)
.............(55)Условие отрыва от Земли
Положим
Введем еще переменные
При таких обозначениях уравнение (55) напишется следующим образом
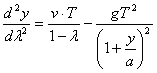 .............(63)
.............(63)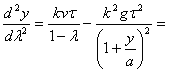 .............(64)
.............(64)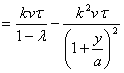 .............(65)
.............(65)Наконец,
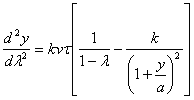 .............(66)
.............(66)Интегрируя, получаем
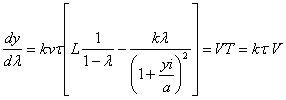 .............(67)
.............(67)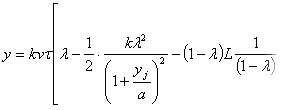 .............(68)
.............(68)Здесь yi и yj обозначают средние, зависящие от λ, величины. В случае, когда можно пренебречь у по сравнению с а, эти уравнения дают
Если в этих формулах положить t=T, т. е. λ = 1, то получим, что при израсходовании всего горючего скорость будет бесконечно большой, но высота подъема будет конечной. Если в (70) положить λ = 1 k=1, получим эту максимальную высоту при данном v. Если принять
| k \ λ | 0.01 | 0.05 | 0.1 | 0.25 | 0.5 | 1.0 |
| 0 0.25 0.4 0.5 0.7 0.9 0.95 0.99 0.999 0.99999 1 |
0 м 138 620 1 371 2 714 3 244 3 829 4 025 4 053 4 057 |
0 м 666 1 824 3 001 6 658 13 241 15 854 18 745 19 718 19 857 19 878 |
0 м 1 269 3 486 5 746 12 816 25 657 30 788 36 491 38 418 38 695 38 739 |
0 м 2 694 7 493 12 454 28 293 57 950 70 071 83 735 88 414 89 093 89 195 |
0 м 3 795 10 908 18 537 44 100 95 258 117 144 142 492 151 395 151 708 152 906 |
0 м 1 218 5 506 11 591 38 250 107 947 142 289 185 076 201 056 203 498 203 874 |
Из этой таблицы видно, что цилиндрическая ракета, т. е. ракета С по постоянным сечениям извержения при скорости последнего 2000 м/с, не будет гореть на высоте более 204 км. При коэффициенте утилизации 1% она будет гореть до 185 км, а при k = 0.5 при том же λ - до 142.5 км.
Скорости V в конце горения получим из (6). Табл. II.
| k\λ | 0 | 0.01 | 0.05 | 0.1 | 0.25 | 0.5 | 1.0 |
| 0 0.25 04 0.5 0.7 0.9 0.95 0.99 0.999 0.9999 1.0 |
0 м 575 1 022 1 386 2 408 4 605 5 991 9 210 13 816 18 421 ∞ |
0 м 570 1 014 1 376 2 394 4 587 5 972 9 191 13 796 18 401 ∞ |
0 м 550 982 1 336 2 338 4 515 5 896 9 111 13 716 18 321 ∞ |
0 м 525 942 1 286 2 268 4 425 5 801 9 012 13 616 18 221 ∞ |
0 м 450 822 1 136 2 058 4 155 5 516 8 715 13 316 1 7921 ∞ |
0 м 325 622 886 1 708 3 705 5 041 8 220 13 817 17 421 ∞ |
0 м 75 222 386 1 008 2 805 4 091 7 230 11 818 16 421 ∞ |
Высота подъема ракеты как снаряда получится из (42)
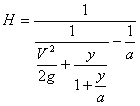 .............(71)
.............(71)Скорость, необходимая для преодоления земного тяготения, равна: 11 180 м/с. Этому условию удовлетворяют три нижних строки таблицы II.
Форма ее определена на стр. 30 уравнением
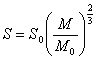 .............(72)
.............(72)Полная ее масса равна
В частном случае
По закону подобия имеем
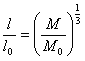 .............(75)
.............(75)Уравнение движения (51) имеет ту же форму, но получает вид
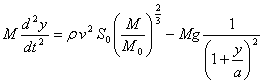 .............(76)
.............(76)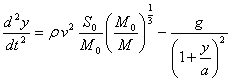 .............(77)
.............(77)Из (74) и (49) имеем
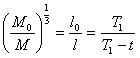 .............(79)
.............(79)Наконец, принимая во внимание (47) и (77)
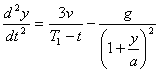 .............(80)
.............(80)Это уравнение идентично с (55), с заменой в нем v через 3v. Назовем эту скорость v1 фиктивной
Из (80) и (81) получаем условие взлета
Положим
Обозначение (60) получает вид
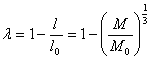 .............(85)
.............(85)Величина (1 - λ) теперь представляет коэффициент линейной утилизации, но не массовой: последний же будет
При таких условиях мы получим те же интегралы, как на стр. 36 с заменой v через v1 = 3v, т. е.
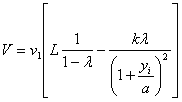 .............(87)
.............(87)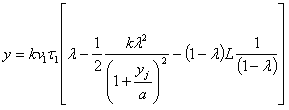 .............(88)
.............(88)Если у мало по сравнению с а, то получаются формулы, аналогичные с таковыми же для цилиндрической ракеты. При равных λ скорость конуса будет в 3 раза больше таковой же цилиндра, а высота в 9 раз больше, формула же (86) показывает, что коэффициент массовой утилизации (u) для конуса, меньше, чем для цилиндра, т. е. первый расходует больше топлива, чем второй.
Теорема стр. 31 и следующей выражают, что при сечениях, одинаковых на единицу массы, цилиндр экономичнее конуса; можно также сравнить конус и цилиндр в отношении одинакового расхода горючего и соответственно изменить теорему.
Для ясности в доказательствах я присвою значек 1 всем количествам, относящимся к конусу, оставляя без этого значка таковые же цилиндра.
Сравним скорости и высоты достигнутые конической и цилиндрической ракетами при одинаковых массовых утилизациях. Из (61) и (86) следует
Откуда
Зададимся случайным λ1; тогда получим соответствующее λ. Например
Чтобы получить соответственно для конуса V и у, следует утроить и удевятерить таковые же для цилиндра при том же λ = 0.5, а затем пересчитать полученные значения для цилиндра при λ = 0.875. Получаем
| k | 0 | 0.01 | 0.05 | 0.1 | 0.5 | 1 |
| у-м | 0 4159 | 5580 4128 | 27 009 4 008 | 51 714 3 858 | 166 833 2 658 | 104 319 1 158 |
| k | 0 | 0.01 | 0.05 | 0.1 | 0.5 | 1 |
| у-м | 0 4159 | 2 492 4 141 | 12 140 4 071 | 23 515 3 984 | 86 370 3 284 | 94 700 2 409 |
Из таблиц видно, что бóльшая живая сила остающейся массы цилиндра компенсирует и повышает разницу в потенциальной энергии, соответствующей разнице в высотах, достигнутых к концу горения. Если, например, остающаяся масса будет 1 кг и k=1, то избыток кинетической энергии цилиндра будет 223 000 кг м, а недостаток его потенциальной энергии около 9600 кг м; из (16) видно, что η цилиндра остается значительно бóльшим, чем конуса при сохранении вышеуказанных условий конформности.
На стр. 30-й мы определили такую ракету условием
Такую ракету можно назвать „экспотенциальной" (степенной) по следующим соображениям
Положим
Напишем (100) в виде
Возьмем производную по t и, учитывая (16), получим
Тогда
Это выражение показывает, что когда z стремится к бесконечности, то х стремится к нулю, т. е. такая ракета имеет бесконечно большие длину и продолжительность горения.
Из (49) и (59) положим
Назовем l действительную длину экспотенциальной ракеты; тогда
Наконец, полная масса ее будет (по 104)
Это показывает, что в такой ракете не только радиус и площадь любого нормального сечения, но и остающаяся масса изменяются по степенному закону в функции длины, что и оправдывает название этой ракеты.
Исходя из (109) и заменяя ρv через ρ'v1 напишем (101) в виде
Это отношение показывает, что L выражает длину цилиндрической ракеты такой же массы и такого же начального сечения, как у рассматриваемой экспотенциальной ракеты.
Уравнение движения
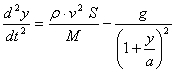 .............(114)
.............(114)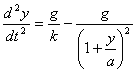 .............(115)
.............(115)Условие отрыва от земли дает
Вводя скорость V, напишем уравнение (115) в виде
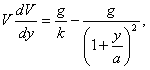 .............(119)
.............(119)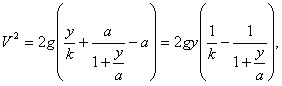 .............(120)
.............(120)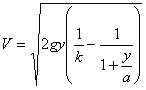 .............(121)
.............(121)Это уравнение кривой (V, у) за период бесконечно продолжительного горения. V растет с у, причем оба возрастают безгранично.
Исключая ![]() из (120) и (44), получим
из (120) и (44), получим
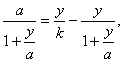 .............(122)
.............(122)Примечание. Так как k < 1, то ус <a
Из (120) и (123) получаем
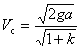 .............(125)
.............(125)Расчет времени; критическое время. Уравнение (121)
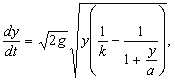 .............(121)
.............(121)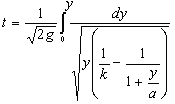 .............(126*)
.............(126*)*Формулы 127-144 помещены в приложении.
Это эллиптический интеграл.
Не имея возможности получить его точно, я решаю ее приближенно (см. приложение в конце этой работы).
Эта ракета представляет особый интерес потому, что дает почти постоянное ускорение, которому подвергаются, как ее части, так и живые существа, которые могут в ней находиться. Я делаю расчет для трех значений ускорений по причинам, которые будут изложены ниже. При этом получаются следующие значения yc, Vc и tc
| Г | k | yс | Vc | tc |
| 10g 2g 1.1g | 0.1 0.5 0.91 | 637 км 3 185 5 800 | 10 660 м/с 9 133 8 080 | 120с 750 36 м 40 с |
Обратные значения ![]() коэффициента утилизации представляют особый интерес; они даны в таблице V для разных значений v
коэффициента утилизации представляют особый интерес; они даны в таблице V для разных значений v
| v м/с | Г=1.1g | Г=2g | Г=10g |
| 2 000 2 500 3 000 3 500 4 000 4 500 5 000 6 000 7 000 8 000 9 000 10 000 |
143000 13270 2700 883 378 196 115 52.2 29.7 19.4 14.0 10.7 |
1574 361.3 135.2 67.1 39.7 26.3 19.1 11.6 8.19 6.30 5.13 4.36 |
358.5 110.6 50.5 28.8 18.9 13.6 10.5 7.10 5.37 4.35 3.69 3.24 |