КЛУБ ЭЛЕКТРОННЫХ ИГР

Эй, ребята на Фобосе! Как вы слышите нас? На своем ракетобусе Мы на марсовом глобусе Приземлимся сейчас. Эй, дежурный на крохотной Марсианской луне! Доложи, что неплохо нам В этом дизельном грохоте, Доносимом извне... Не завидуйте, братья, нам: Нас никто не встречал. Над цепочкою кратерной Для себя основательный Сами ищем причал...

ГЛЯДИ В ОБА —
ВПЕРЕДИ ФОБОС!

Энергичные строки Виктории Багинской из Краснодара как нельзя лучше соответствуют настроениям участников рейса «Кон-Тики», совершивших по заданию редакции еще и перелет из окрестностей Марса на его естественный спутник (см. «ТМ» № 11 за 1985 год). На этот раз, помимо традиционного «математического» отчета, состоящего в основном из цифр, кратких пояснений и фрагментов программ, требовалось представить и «литотчет» о полете объемом в 3–4 страницы. Впрочем, один из предполагаемых победителей нашего «астропробега», 25-летний инженер-механик Александр Артамонов из подмосковного города Апрелевки вместо представления полновесного художественного отчета ограничился расширением своей пояснительной записки: «Задачу о перелете со станции, вращающейся на орбите Марса, на Фобос решить «в лоб», методом обычного пилотирования, очень трудно. Дело в хронической нехватке горючего, возникающей из-за неэкономичного режима полета. Наиболее оптимальным выглядит следующий сценарий перелета. Стартовав со станции, разогнать корабль до вертикальной скорости 1000–1300 м/с. Затем, регулируя тягу двигателей, поддерживать горизонтальную скорость корабля, равной первой космической для данной высоты. Если скорость меньше, возникают энергетические потери, связанные с преодолением силы тяготения; если больше, вертикальная скорость начнет увеличиваться и возникнет необходимость в дополнительных затратах на торможение... На высоте порядка 7500–8000 км выключить двигатель и перейти в свободный полет. Под действием силы Кориолиса горизонтальная скорость корабля начнет уменьшаться. Когда она станет меньше первой космической, вертикальная скорость начнет уменьшаться также. Не долетая 40–50 км до орбиты Фобоса, включить двигатель и начать активное торможение. На расстоянии 10–20 км от его поверхности перейти на программу ОС-3 и продолжать полет в окрестностях спутника. Посадку удобно производить в центре видимой либо невидимой стороны или же в центре «переднего» либо «заднего» (по ходу движения спутника) полушария. В этих точках удобно контролировать качество посадки».

В ЦУП-ТМ этот отчет был засчитан, как и ответы Анатолия Колосова из села Пышуг Костромской области, Андрея Долгалло из Ленинграда и Сергея Вардина из Москвы, представивших на этот раз только цифры, зато в предыдущих турах весьма красочно описавших свои злоключения при орбитальных и суборбитальных вылазках. Кстати, именно на пути к Фобосу роковая катастрофа подстерегла автора термина ЦУП-ТМ Александра Морева из Устинова: «В конце ноября бортовой компьютер (марки МК-56) моего космического корабля совершил несанкционированный полет со стола на пол и полностью вышел из строя. Попытки оживить его собственными силами не увенчались успехом. Сервисные службы обещали восстановить моего друга и помощника в лучшем случае к середине февраля. В результате этой аварии я отстал от основной группы участников перелета на три месяца...»

Другие вероятные победители астропробега ответили редакции дружным залпом основательно проработанных текстов. Администрация КЭИ не без оснований считает эти произведения первыми в мире документальными воспоминаниями людей, самостоятельно (а не в каких-то там фантастических романах) совершивших такое путешествие.

Но прежде чем перейти к этим уникальным свидетельствам, сделаем краткий обзор тех заданий по № 10ndash;11 за 1985 год, исчерпывающий ответ на которые не содержался в отчете А. Перепелкина. Собственно, таковых было два: указать оптимальную схему перелета на станцию «ЮГ» и подобрать для каждой планеты Солнечной системы ее «вечернюю» (или «утреннюю») звезду. С первым все справились единообразно: вывели «Кон-Тики» на низкую круговую орбиту, выждали, пока корабль приблизится к станции, а после этого пошли на причаливание. (Кстати, именно так поступают в аналогичных ситуациях и «взаправдашние» космонавты.) Второе затруднений также не вызвало: для каждой планеты функции «вечерней» звезды выполняет ее ближайшая со стороны Солнца соседка; это прямо следует из приближенного правила Боде-Тициуса, согласно которому радиусы планетных орбит примерно подчиняются геометрической прогрессии. «Вечерней» звезды лишен Юпитер – ее роль могут играть лишь астероиды, а они чересчур слабы, чтобы видеть их невооруженным глазом. Правда, неугомонный своих критических замечаниях Лев Роканиди указал, что «вечерними» звездами обделены также Плутон и Нептун: с них, дескать, предыдущие планеты (Нептун и Уран) различимы не лучше, чем с Земли, а поскольку с Земли их не видно, то... Однако администрация КЭИ с оригинальничаньями отдельных участников перелета (то они программы какие-то выдумывают, то видеосообщения, то им, видите ли, универсальный обнулитель «1-00» не нравится, то еще что-нибудь) уже свыклась и поняла, что все они преследуют одну-единственную цель: любой ценой затянуть отсылку очередного ответа! Да никто этого вроде и не скрывает. Например, Роканиди: «Нужно было написать два отчета о полетах. Именно они вызвали задержку в отправке письма, ибо летать куда легче, чем писать».

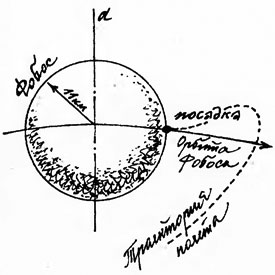
Маневрирование в окрестностях Фобоса (по эскизу А. Артамонова).

Именно так: летать легче, чем писать! Ну-ну! Впрочем, перевернем страницу отчета:

«На причальной мачте марсианской орбитальной станции «Джонатан Свифт» висит лунолет № 37000. Кто и с какой целью дорисовал три лишних нуля, до сих пор неизвестно. Ясно лишь то, что это произошло, вероятно, еще на Земле. А так как исправлять индексы в Космофлоте всеми инструкциями и правилами категорически запрещается, все сорок лет эксплуатации безвинная машина пролетала с нелепым числом на борту. Пользовались ею в последние годы редко: показать какому-нибудь инспектору орбитальное хозяйство или небольшой груз подвезти, почту...

Например, этот ящик, расположившийся в штурманском кресле. На нем размашистая надпись мелом: «100 кг. До Фобоса. Резче 3 g не дергать». Напротив сижу я. Гляжу, как ползет стрелка по топливной шкале. Через некоторое время она добирается до ограничителя: 3500 кг. Что-то лязгает об обшивку. Магнитный захват освобождает суденышко, мачта отходит в сторону. Индикатор на пульте загорается мягким зеленым светом. Можно лететь.

Нажатием кнопки запрашиваю навигационную систему о полетной обстановке: до Фобоса 15 мегаметров по горизонтали и 6 по вертикали. Значит, обгоняет станцию «ДС» на четверть витка. Понятия не имею, какие из этого делать выводы и как планировать рейс. В таких случаях надо руководствоваться принципом «не мудри». Поэтому начинаю разгон самым естественным образом: полный вперед (90°), 250 кг за 6 с. Дважды нажимаю клавишу «Пуск». Двигатель грохочет, терзая барабанные перепонки. Машину трясет и дергает хуже телеги на булыжной мостовой. Отяжелевшей почти втрое рукой сдвигаю рычаг расхода на двухсоткилограммовую отметку и вновь дважды подаю команду на двигатель. Затем еще одну: 170 кг за 5 с. Пожалуй, хватит на первый раз. Наступает тишина. Она вливается в уши, как холодная речная вода, когда, войдя по колено и ежась от утренней прохлады, бухаешься в нее с размаху, подняв тучи брызг. В этой тишине слышно, как распрямляется прогнутая на разгоне обшивка кресел. Приходится приложить усилие, чтобы руки опустились на пульт. Смотрю скорость: по авиационным меркам два маха с хвостиком.

Внизу, в легкой дымке, дневная сторона Марса. Фобоса не вижу, хотя и должен бы, пусть в виде звездочки. Зрелище из полусферы кабины предстает, безусловно, величественное и прекрасное. Тут тебе и Солнце, и звезды, и Луна, и Земля, и все это сразу вместе... По моим расчетам, межорбитальный переход займет час-полтора. Надо было прихватить журнал, да не подумал в спешке. Время движется медленно, нехотя прибавляя секунду за секундой к показаниям борт-хронометра. Его круглый циферблат разбит на 300 делений, один круг стрелка завершает за пять минут. Пять минут, пять коротких, как вспышка молнии, рабочих минут он обращает бесконечными тремястами секундами.

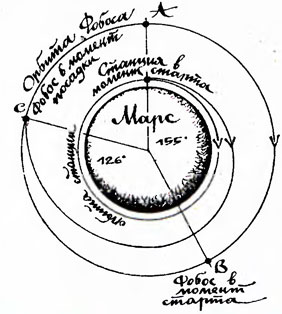
Полет к Фобосу (по эскизу В. Ладохина).

Так проходит 1 час 25 минут, или 5100 секунд. Семнадцать раз по бесконечности. Открываю глаза и вижу сияющий шарик Фобоса. Он выглядит крупнее Луны. Осталось 815 км вверх и 609 вперед да скорости уравнять: сбросить излишек вертикальной (574 м/с) и скомпенсировать недостаток горизонтальной (-366 м/с). Ставлю рычаги на 200 кг за 6 с, угол тяги прежний, 90°. Два раза запускаю двигатель. Перегрузка вплотную приближается к трехкратной. Еще 200 кг: увеличиваю на секунду время маневра. Наконец последний импульс: 150 кг за 5 с. После отсечки двигателя отдыхаю 4×300=1200 с. Ровно двадцать минут. За это время горизонтальная скорость снижается до 96 м/с, вертикальная достигает 635. Будем гасить вертикальную: 180°, 150 кг, 6 с. Четырежды отправляю топливо в дюзы. От 635 м/с остаются ничтожные 17 — всего 60 км/ч. А вверх идти 61 км. Пожалуй, маловато. Впрочем, как образно выражался наш инструктор по пилотажу, «не жалейте вертикальной скорости при подъеме, она скушает горизонтальную и поправит свои дела».

Что ж, можно опять отдохнуть. Тишина длится ровно четыре оборота стрелки бортового хронометра. По приборам скорости 62 и 81, расстояния 13 и 88 км — соответственно по вертикальной и горизонтальной осям координат. Опять пора гасить вертикальную скорость: 180°, 60 кг, 3 с. По завершении маневра разворачиваю суденышко вверх носом.

Серая, бугристая, покрытая мелкими «озерами» кратеров глыба Фобоса заполняет собою небо. Уже видны мерцающие огоньки посадочной площадки. Пора переключать аппаратуру в режим ближней навигации. Смотрю на часы: прошло еще три «пятиминутки». Но двигатель включать рано. Жду 20 секунд, потом еще 5. Рычаги стоят на 90°, 70 кг и 4,5 с. Остается нажать клавишу. Горизонтальная скорость зануляется, вертикальная равна 29 м/с. Ставлю 180°, 25,3 кг и 3,1 с и спустя 64 с даю импульс. Пока команда исполняется, передвигаю все три рычага. Новый рывок: 90°, 2 кг, 0,3 с. Тень лунолета бежит по неровной поверхности. Не проходит и минуты, как амортизаторы касаются грунта. Корпус кренится вперед, но шипы посадочных опор держат надежно.

Остается добавить для проверки, что всего на пульт было подано ровно 49 команд».

В тексте Л. Роканиди есть все необходимые цифры, он может служить проверочным тестом для программ ОС-1 и ОС-3. Вполне содержательные отчеты представили также Вадим Ладохин (Сургут), Павел Трубаев (Белгород), Сергей Свинолобов (Днепропетровск). Последний, кстати, вышел на старт позже других участников: МК-54 появился у него лишь в конце прошлого года. Однако после выполнения конкурсных заданий, а также дополнительного (перелет на станцию «ЮГ» с последовательным использованием программ ОС-1 и ОС-2) он был допущен к участию в перелете и быстро утвердился в лидирующей группе.

Надо сказать, что кое-кто из наших ведущих пилотов шагнул довольно далеко за рамки предлагавшегося задания. Так, десятиклассник Юрий Кузнецов из Куйбышева главный упор в отчете о полете «Тигриса» (так он окрестил свой корабль) сделал на историю околомарсианской базы «Галлей»: ее основой послужил астероид 2508 Алупка, открытый в 1977 году астрономом Н. Черных и после нескольких сближений с Вестой и Юпитером захваченный притяжением Марса. Решением Центрального Управления Космических Исследований, как сообщил Юрий, астероид переоборудовали в станцию. «Внутренняя часть использовалась как гигантский топливный бак вместимостью около 10 км³, а оболочка, покрытая теплозащитным экраном, служила стартовой площадкой для космолетов, взлетающих или садящихся на Марс. Отсюда космические корабли направлялись к Фобосу, где дозаправлялись и продолжали полет».

«На зыбкой почве фантастики» согласно собственному чистосердечному признанию возвел здание своего «репортажа» грузчик-механизатор из Запорожья Александр Аула:

«— Вахтенный вычислитель, к капитану, — раздался по селектору голос старпома. Когда Байт, так звали молодого, подающего надежды вычислителя, вошел в ходовую рубку «Паруса», его ждали капитан, старпом и вахтенный пилот Лун Кор.

— Дружище Байт, — обратился капитан к вошедшему, — сделай расчеты прямого на Фобос и обратного полетов, эта часть программы нужна сегодня. Кроме того, после отхода «Кон-Тики» данные бортового вычислительного комплекса по радиоинтерфейсу держать в Большом Компьютере, чтобы в случае чего сразу выдать данные для коррекции.

— Слушаюсь, капитан, но в тени Марса возможны сбои, — ответил Байт.

— Сбоев не должно быть, Байт. Станция ОС-1 только что выведена на орбиту...»

И так далее. Правда, о самом перелете на спутник информации в «репортаже» Александра почти нет: гораздо больше внимания уделяется подготовке старта звездолета «Парус» в направлении Альфы Центавра. Тем не менее он отнесся к экспедиции на Фобос со всей возможной основательностью — слетал туда несколько раз, причем воспользовался на втором участке, помимо программы ОС-3, и программой «Лунолет-4»: это дало возможность оценить влияние собственного тяготения Фобоса на движение корабля. Как и следовало ожидать, оно оказалось очень незначительным.

Думается, что с эмоциональной стороной перелета на Фобос все более-менее ясно. Те же, кого в процессе посадки на этот спутник (и на другие небесные тела) больше интересуют физико-математические аспекты дела, могут найти довольно исчерпывающие сведения на этот счет в статье «Последний дюйм» (стр. 59).

Остается добавить, что на практике перелет со спутника на спутник впервые осуществили советские космонавты Леонид Кизим и Владимир Соловьев, успешно прошедшие 5–6 мая 1986 года на корабле «Союз Т-15» по маршруту: станция «Мир» — станция «Салют-7».

Кстати, первоначально корабль отставал от «Салюта»; перед космонавтами стояла примерно та же задача, какую решали читатели, догоняя станцию «ЮГ». И решена она была практически так же: торможение с последующим выходом в район станции. Операция, правда, заняла не один, а 16 витков — но и отставание было гораздо больше (3 тыс. км вместо 250 для «Кон-Тики»).

Многие читатели, интересующиеся в первую очередь нестандартными способами работы с ПМК, а также методами временного вывода машинки из строя, обращают внимание на «пустышку» (или «точку», как ее иногда называют), способ образования которой (Сх ÷ ВП КНОП) был вскользь упомянут в № 12 за 1985 год.

«Эту точку можно даже записать в память, — делится опытом восьмиклассник В. Суворов из Свердловска, — и больше практически ничего. Даже не сложить 2+2, а в программной памяти вообще ужас! Можно делить на 0 — получится 0. Эта серия команд очень похожа на встречу автоматов с Тьмой: приборы выходят из строя, пленки засвечиваются и т. д.».

«Точка — сигнал капризный, — пишет восьмиклассник М. Рыжков из Новосибирска, — плохо записывается в память, лучше всего в регистр А. Сразу после формирования попробуйте перейти в режим ПРГ. Удивительная вещь! Счетчик шагов скачет совершенно произвольно, коды не соответствуют командам, иногда возникает вообще чепуха. Точку не так-то просто убрать. После Сх машина работает ненормально: не производит никаких действий, ни с того ни с сего начинает работать программа или машина вообще «уходит в себя», как йог. Вывести из этого состояния может лишь отключение».

«Посмотрите сами — не обрадуетесь, — резюмирует восьмиклассник из Москвы С. Банников. — Это неисправимо». «Не проходит ни одна команда... Караул! — вторит ему десятиклассник А. Степанов из Куйбышева. — ПМК не слушается, а может, он и слушается, но я ввел своей командой (точка) новый код».

Довольно детальный анализ представил П. Кузнецов из Ленинграда: «Точки. Это название я дал по их типичному представителю (Сх К7 ВП КНОП). «Точки» вообще (та же операция над несколькими нулями), попросту говоря, пустое место на месте (каламбур) первой значащей цифры мантиссы. Разновидности точек можно получить командой 1/x от чудовищ-хвостов ОС-оборотней (только от них) — «ненормальный» случай, так как должна вроде бы получиться Тьма: 1000-430=570, уровень Тьмы. Точки очень коварны — пока они находятся в стеке, многие команды не выполняются или коверкаются. Программирование лучше в это время не включать — программа будет испорчена, а на индикаторе будет твориться черт-те что: режим ПРГ выйдет из строя. Если же особенно долго измываться над точкой, то в режиме ПРГ это будет уже не временно, а постоянно и ПМК придется выключить. Точки также имеют привычку «сбегать» — могут перемещаться из одного регистра в другой, сдвигая заодно за собой по кругу содержимое остальных регистров и вызывая по ходу передвижения некоторые побочные явления. Это свойство точек было бы очень ценно, если бы они не портили программу. А так как такое передвижение в регистрах все равно возможно, то почему бы разработчикам ПМК не сделать его осуществимым специальными командами в следующих моделях?»

И действительно, почему бы? Но вернемся к своей Б3-34 (МК-54). У каждого отрицательного явления есть свои плюсы. Есть они и у «пустышки». Кстати, П. Кузнецов прав: имеет смысл говорить о целом классе таких объектов: если процесс формирования начать не с нуля, а с нескольких (например, Сх 000 ÷ ВП КНОП), получим «пустышки», завершающиеся несколькими нулями (в данном случае двумя). Наиболее «опасны» самые «старшие» из них (получившиеся из семи либо восьми нулей); с ними то, о чем пойдет речь, не проходит. Зато все остальные сойдут вполне.

Для начала сформулируем алгоритм полной «ликвидации» таких объектов: при появлении на индикаторе «пустышки» нужно семь раз подряд нажать стрелку вверх. Стек полностью очищается. А теперь займемся делом.

Как известно, в регистры Б3-34 можно записать лишь 14 чисел. Так вот, «пустышка» позволяет запомнить еще три (правда, не всяких — подходящие числа ограничены как по порядку, так и по длине мантиссы).

Запишем для начала в регистр 9, скажем, число 111111 (шесть единиц). Затем по стандартному алгоритму получим любую из «младших» пустышек. Теперь нужно нажать стрелку вверх, ИП9 и еще пять раз стрелку вверх. «Пустышка» ликвидирована, а число 111111 куда-то записано (но куда, никому не известно).

Повторим ту же процедуру еще дважды, записав в первом случае в регистр 9, скажем, число 222222 (шесть двоек), а во втором — 333333 (шесть троек). «Пустышка», фигурирующая в каждой операции, может быть любой, но обязательно из «младших». По завершении операции все три числа (111111, 222222 и 333333) оказываются куда-то записаны!

После «ликвидации» последней «пустышки» можете смело вводить в свой ПМК любую сколь угодно сложную программу, использующую подпрограммы, циклы, команды косвенной адресации, занимающую все ячейки памяти и использующую все адресуемые регистры. Поработав с ней хоть целый день, сформируйте какую-нибудь «пустышку» (из «младших») и примените к ней алгоритм «ликвидации». Вы увидите на индикаторе последовательно два из записанных чисел: 222222 и 111111. А если вместо алгоритма «ликвидации» дважды нажать XY, глазам предстанет другая пара: 333333 и 222222.

Администрация КЭИ обычно использует этот способ для запоминания шестизначных телефонных номеров (семизначных удается записать только два).

Еще об одном полезном свойстве «пустышки» рассказывает наш постоянный корреспондент Дмитрий Кайков из Белгорода:

«Используя точку, можно получать и шифры. Сделаем вот что: 10 F1/x ПА Сх ÷ ВП ПД ИПА П0 1 П0 П0 ПВ. Теперь нажмем «сброс» (Сх) и, нажимая на стрелку вверх, будем сбрасывать все появляющиеся числа. Теперь вызовем из регистра В код 01 30. Можно избавиться от порядка: ВП /-/ 30 ПВ. Этот код (01) можно использовать в программе. Оператор /-/ меняет ноль в самом левом разряде на L. Поманипулировав операторами КИП, ВП, /-/ и т. д., можно получать разные другие коды (например, применив к исходному сообщению 01 последовательность /-/ П0 КИП0 ИП0, получим L-------0. Только стоит внимательно и осторожно обращаться с кодами, у которых второй разряд (я считаю слева, включая и самый первый) пуст. Такой код, например, можно получить из 01, записанного в регистре В (или любом другом) командой КИПВ. Этого шифра и ему подобных, как и «точки», следует опасаться, так как может произойти путаница в программной памяти и даже в стеке».

Если у кого-нибудь есть информация о еще каких-то полезных применениях «пустышки» и родственных ей символов, просим дать знать.

Михаил ПУХОВ

ПОСЛЕДНИЙ ДЮЙМ

«Все дело в том, чтобы правильно рассчитать, — сказал Бен. — Когда выравниваешь самолет, надо, чтобы расстояние до земли было шесть дюймов. Не фут и не три, а ровно шесть дюймов! Если взять выше, то стукнешься при посадке и повредишь самолет. Слишком низко — попадешь на кочку и перевернешься. Все дело в последнем дюйме...»

Легко догадаться, что наше очередное занятие не случайно открывается цитатой из хрестоматийного рассказа Джеймса Олдриджа. Разговор пойдет об алгоритмах посадки. А поможет нам, как обычно, посадочный модуль, изготовленный художником Евгением Катышевым.

Итак, первое упражнение — «приземление» на планету достаточно большую, чтобы можно было пренебречь ее шарообразностью и считать плоской. Теперь обратимся к блок-схеме алгоритма. Прежде всего вводятся исходные данные — характеристики планеты и корабля, начальные значения переменных. Затем следует блок сравнения. В момент старта высота, конечно, неотрицательна (выход из ромба по стрелке «нет»), и настает пора брать в руки штурвал — задавать значения управляющих параметров. После этого включаются блоки определения реактивного ускорения и вычисления переменных: их устройство известно по предыдущим выпускам (см. «ТМ» № 5, 6 за 1986 год). Полученные результаты выводятся на индикатор, но предварительно проверяется высота. Пока полет проходит вдали от поверхности, никаких проблем не возникает, ведь «все дело в последнем дюйме». Но если ошибка летчика в момент приземления может оказаться роковой, то наш бортовой компьютер корректирует действия экипажа. Как же это происходит?

Проанализируем алгоритм посадки на последнем маневре. Если вам удалось, снизившись почти до поверхности, погасить скорость летательного аппарата, то проще всего либо совсем выключить двигатель, либо малой тягой частично скомпенсировать силу тяжести, чтобы суммарное ускорение было направлено вниз. Лунолет падает с небольшой высоты, и его вертикальная скорость попросту не успевает выйти за допустимые пределы.

Подобрать время финального маневра так, чтобы в момент его завершения высота в точности обратилась в нуль, затруднительно. Скорее всего аппарат «заглубится» в поверхностные слои планеты. В этом случае мы выходим из блока проверки по стрелке «нет» и микрокалькулятору надо подкорректировать посадку. С методом коррекции путем половинного деления мы уже знакомы (см. «ТМ» № 6 за 1986 год). Обсуждаемый сегодня способ отличается существенным (особенно для ПМК) достоинством — он работает («сходится») гораздо быстрее.

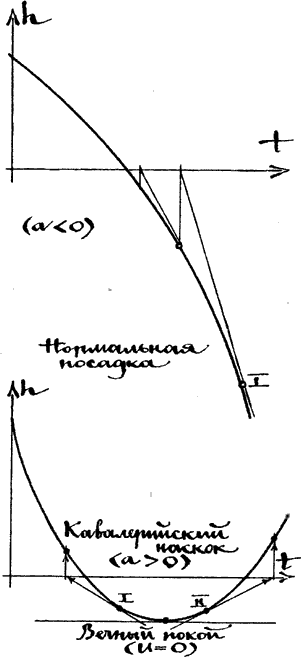
Как и в прошлом выпуске, наш электронный помощник играет роль своеобразной машины времени, возвращающей аппарат по траектории назад, в точку касания с поверхностью. Разделив высоту на вертикальную скорость (та и другая отрицательны) и поменяв знак полученного числа, он находит отрицательное время «шага назад», подставляет его в уравнения движения и подтаскивает лунолет ближе к поверхности. За один шаг выбраться из «подземелья» обычно не удается (см. график зависимости высоты от времени, случай «нормальная посадка»).

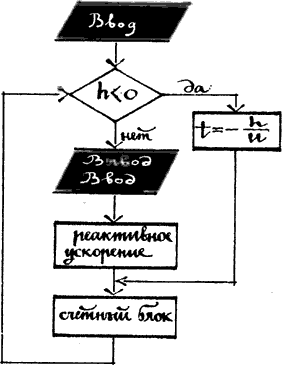
Поясним, в чем дело. Для тех, кто знаком с понятием производной, не составит труда доказать, что в любой точке тангенс угла наклона касательной к кривой h(t) равен значению вертикальной скорости в этот момент времени. Поэтому геометрически алгоритм можно иллюстрировать так — в той точке, где оказался аппарат в результате последнего маневра, к графику проводится касательная, пересечение ее с временной осью и определяет величину «шага назад». Из графика видно, что мы пока еще остались под поверхностью небесного тела. (Выйти за один шаг можно только в случае прямолинейного графика, то есть равномерного спуска.) Теперь цикл повторяется — так как высота отрицательна, то из блока проверки мы опять выходим по стрелке «нет» и снова делаем «шаг назад». И так далее. В результате всего за несколько шагов высота (в пределах заданной точности) обращается в ноль — лунолет на поверхности, а уж в каком состоянии, это зависит от скорости.

«Цель расчетов не число, а понимание», — утверждают многие математики. Если посмотреть на наш алгоритм с этой точки зрения, то нетрудно увидеть, что фактически мы приближенно решили уравнение h(t)=0. Следует признаться: описанный процесс придуман давным-давно и носит название «метода касательных». Надеемся, он пригодится читателям и при решении других задач.

Наряду с осторожными космолетчиками встречаются у нас в КЭИ и любители острых ощущений. Их стиль пилотирования — маневры с предельными перегрузками, «полет на грани реанимации». Если корабль космического лихача окажется «под землей», то коррекция приводит к неожиданным результатам (случай «кавалерийский наскок»). Хотя метод остался прежним (личные качества пилота калькулятором не учитываются), вид кривой h(t) изменился. Если теперь сделать «шаг назад», то мы окажемся не под, а над поверхностью планеты. Корабль как бы подбросило вверх (см. «ТМ» № 3 за 1986 год). Посовещавшись, мы решили назвать это явление «эффектом пороховой бочки» (ЭПБ) — в самом деле, представьте себе, что вы, дав полную тягу, пытаетесь приземлиться на площадку, вымощенную толовыми шашками.

Возможен и другой случай. Если аппарат проскочит вершину параболы, то «шаг назад» сменится «шагом вперед». Корабль как бы «рикошетирует». Те, кто сажал «Кон-Тики» в океан, возможно, уже столкнулись с этим явлением.

Наконец, может получиться так, что в результате посадочного маневра аппарат окажется в точке «вечный покой». Вертикальная скорость при этом равна нулю и при попытке деления на индикатор выводится сигнал ошибки — лунолет навечно погребен в недрах планеты, обратной дороги нет.

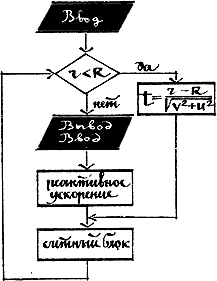
А теперь второе упражнение — посадка на сферическое небесное тело сравнительно малых размеров. Поверхность его может иметь неровности: посадка считается завершенной, если отклонение от средней поверхности шара не превышает некоторой, заранее заданной величины (в программе «ОС-3» — 1 м).

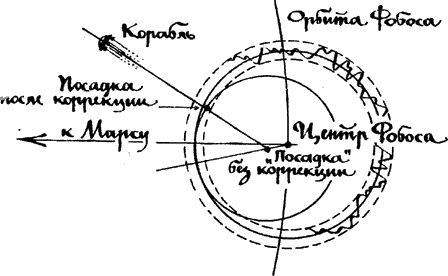
Если в результате маневра корабль оказался внутри сферы (точка «посадка без коррекции»), то ПМК определяет кратчайшее расстояние до поверхности и, разделив его на модуль скорости, делает «шаг назад», а в случае необходимости и несколько. В ситуации, изображенной на рисунке, достаточно однократной коррекции.

Описанные в этом и предыдущих выпусках способы коррекции посадки, по сути дела, представляют собой различные методы решения уравнений. В зависимости от применяемого варианта возникают дополнительные физические эффекты (ЭПБ, рикошет). С другой стороны, решая ту или иную задачу, важно умело выбирать математический аппарат, чтобы наиболее полно учесть все существенные факторы. Собственно, искусство программирования и состоит в построении наиболее точной модели и алгоритмизации изучаемого процесса, а сама программа — это, как говорится, дело техники, правда, порой довольно виртуозной.

«Последний дюйм, который разделяет всех и вся, нелегко преодолеть, если не быть мастером своего дела. Но быть мастером своего дела — обязанность летчика». Эти слова Дж. Олдриджа можно адресовать представителям любой профессии.

Сергей ВОЛКОВ,
инженер