КЛУБ ЭЛЕКТРОННЫХ ИГР

СДЕЛАЙ САМ СЕБЕ РАКЕТУ

Как видим, наше клубное помещение постепенно обставляется новой мебелью (блок-схемами), виртуозно сработанной художником Евгением Катышевым. Из-за этой замечательной мебели (блок-схем) оно все больше теряет привычные контуры детской площадки для игр, становясь похожим скорее на научную лабораторию или в крайнем случае на машинное отделение (отсек, в котором стоят ЭВМ) какого-нибудь фантастического фотонно-подпространственного звездолета...

Впрочем, надо признать со всей откровенностью: для многих читателей нашей рубрики всякие игры кончились уже после выхода «ТМ» № 9 за прошлый год. Космонавтика, как выяснилось, не игра, а работа, и работа довольно-таки утомительная. «При орбитальных переходах... слишком долго ждать результата. Виток, два витка, иногда больше. Причем каждый виток — это полтора часа, два... Вот и крутишься. Изматывает...» — так характеризовал ситуацию М. Коршунов. Можно, конечно, махнуть рукой на цели и задачи «Кон-Тики» и просто играть. Так, О. Роженцов из города Голицына Московской области взял большой лист миллиметровки, начертил замысловатый лабиринт, ввел в ПМК программу «Лунолет-2» и... Вот что он рассказывает: «Изменяется просто смысл игры. Теперь она заключается в прохождении корабля по лабиринту. Цель может быть разной (например, сесть в то же место, если трасса замкнута). Исходные данные лучше изменить: ускорение свободного падения задать равным нулю, уменьшить скорость истечения продуктов сгорания, разместить в лабиринте промежуточные заправочные станции и т. д. Эту игру можно использовать и для двух игроков с двумя ПМК, например устроить гонки на трассе...»

А вот еще один небезынтересный опыт. «Получил массу удовольствия, гоняя на «Кон-Тики» по всей Луне, — пишет А. Арсеньев из города Березники Пермской области. — Получил немало «шишек», много моих «могил», увенчанных обломками «Кон-Тики», осталось на поверхности нашего естественного спутника. Методом «тыка и вытыка», как у нас говорят, освоил выход на орбиту и сход с нее. К сожалению, дефицит свободного времени не позволил мне принять участие в перелете на Землю. Поэтому, начиная со стыковки со станцией «Юрий Гагарин», я стал наблюдателем и болельщиком. Уже в окололунном орбитальном полете начинает ощущаться недостаточный динамизм обстановки. Виной тому — малый шаг приращения времени и фактическое бессилие оператора, «болтающегося» на орбите. Именно из-за этого я увлекся «высшим пилотажем»: не выключая двигателя, меняя лишь направление вектора тяги, делал мертвую петлю в горизонтальном полете на небольшой высоте...»

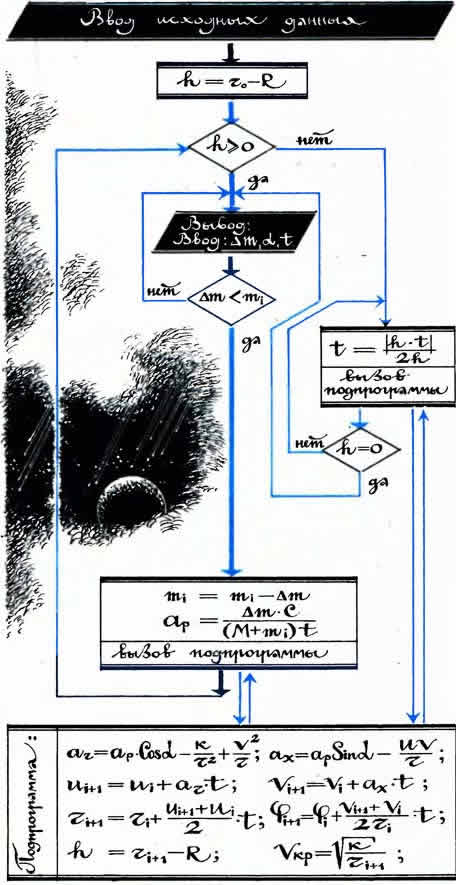
Тем не менее, несмотря на все объективные и субъективные трудности (присутствующие, кстати, и в реальном полете), большая группа читателей не только аккуратно выполняла предлагавшиеся задания, но и ежемесячно представляла в редакцию (ЦУП-«ТМ», как метко окрестил КЭИ А. Морев из Устинова) объемистые отчеты о каждом этапе полета. Основным «транспортным средством» для тренировочных орбитальных полетов служили программы «Лунолет-3» и «Вершина». Их обобщенная блок-схема приведена на рисунке, ее подробное описание можно найти в разделе «Алгоритмическая гимнастика». Дополнительно к программе «Лунолет-2» введены следующие постоянные и переменные величины: K — гравитационная постоянная планеты, равная произведению квадрата ее радиуса на ускорение свободного падения на поверхности; R — радиус планеты; r — текущее расстояние от ее центра; φ — угловая координата; V_кр — круговая скорость на данной высоте. Рельеф учитывается заданием какой-либо зависимости радиуса планеты от угловой координаты.

Программы «Лунолет-3» и «Вершина» реализуют упрощенные варианты приведенной блок-схемы. В первой из них счетный блок сохранен полностью, зато использован упрощенный посадочный блок, подробно описанный в «ТМ» № 3–4 за этот год. Радиус планеты считается постоянным. Конкурсное задание по «кругосветному» путешествию особых затруднений не вызвало (разумеется, у тех читателей, кто благополучно справился с баллистическим перелетом на 250 км). Что же касается «скрытых» возможностей ПМК (а участники перелета, и это радует, проявили себя не только мужественными пилотами, но и высококвалифицированными бортинженерами: смело вносили изменения в опубликованные программы и разрабатывали свои собственные), надо отметить предложение десятиклассника Льва Роканиди из Сызрани: хотя он несколько задержался с представлением отчета, зато придумал оригинальный способ преобразования сообщения (Е -0) в (Е 0-) с помощью команды ВП 9 КНОП. Этот способ, по убеждению администрации, открывает пути дальнейшего совершенствования данной серии космических аппаратов.

«Кон-Тики» выходил на орбиту по-разному, но на это всегда уходило несколько больше двух тонн топлива (вспомним: «Ракете легче финишировать, чем стартовать, потому что на финише она сама легче»). Приведем, например, мнение А. Артамонова из города Апрелевки Московской области. «Режим вывода аппарата на орбиту таков. Сначала его нужно разогнать на малой высоте до первой космической скорости. При этом израсходуется большая часть топлива и аппарат станет легче примерно на 2 т. Затем (достигнув нужной высоты. — М. П.) придать ему дополнительный корректирующий импульс и вывести на круговую орбиту. Как указано в тексте, никаких особых препятствий, кроме горного хребта на обратной стороне Луны, на пути аппарата нет. Поэтому разгон на малой высоте, по-видимому, можно считать допустимым».

Надо сказать, что участники тренировочных рейсов в ряде случаев оценивали свои действия без намека на зазнайство и хвастовство, с ощутимым элементом самокритичности. «Несколько дней и ночей, отрываясь нехотя лишь на еду и кратковременный сон, я методично разбивал лунолет за лунолетом, «размазывая» их по поверхности», — пишет студент ЛГУ Д. Журавлев, делясь своим первым опытом пилотирования ракетных аппаратов. «Посадка без больших повреждений, — рапортует А. Морев. — Недолет, правда, порядка 1500 м. Но, вероятно, посадочная площадка космодрома позволит мне несколько удалиться от ее центра». И так далее.

В программе «Вершина» гравитационное, кориолисово и центробежное ускорения не зависят от высоты, зато имеется рельеф: отклонение радиуса планеты от нулевой отметки в окрестностях начала координат задается колоколообразной кривой, носящей красивое математическое название «локон Аньези». Кроме того, в «Вершине» использован тот же посадочный блок, что и на нашей блок-схеме. Все тот же неутомимый в своих критических замечаниях Л. Роканиди и С. Вардин из Москвы выражают (в письменной форме!) свои сомнения по поводу рекомендуемой для программ «Вершина» и «Маскон» формулы для расчета круговой скорости; по их мнению, команду ИП7 следует заменить на ИПА, ибо, по словам С. Вардина, «из текста следует, что от высоты не зависит ускорение силы тяжести, а не круговая скорость (что было бы странно!)».

Необходимо дать пояснение. Как уже отмечалось, сила тяжести в этих программах считается постоянной. Естественно, это верно лишь в узком приповерхностном слое. Поэтому круговая скорость в программе «Вершина» действительно не зависит от высоты; если согласиться с поступившими предложениями, она, вместо того чтобы уменьшаться с высотой, увеличивалась бы (что было бы действительно странно!). Впрочем, при полетах на малых высотах это особого значения не имеет.

М. Точин из Вологды, Ю. Кузнецов из Куйбышева и А. Аула из Запорожья сообщили, что в программе «Вершина», по их мнению, содержится ошибка: происходит ее зацикливание, причем команда с пульта С/П В/О С/П не помогает — программа снова зацикливается. Естественно, критика предлагается конструктивная — все трое изобрели различные методы устранения неприятности, основанные на модернизации алгоритма посадки. Однако главное достоинство посадочного блока программы «Вершина» — возможность выполнения посадки на крутом склоне, причем даже в горизонтальном полете, — при этом теряется.

Разбор показал:

1. После ввода исходных данных, опубликованных в журнале, лунолет в начальной позиции находится, как правильно подметил М. Точин, на высоте -6,2 м, то есть как бы в стартовом колодце. Причина в том, что подошва горы, перелет на которую надлежит выполнить, тянется довольно далеко. Если стартового импульса не хватает, чтобы вывести корабль из колодца, программа действительно зацикливается (это легко проследить по блок-схеме). Если же импульс достаточен, никакого зацикливания не происходит и можно смело лететь дальше.

2. Из-за медленной сходимости метода половинного деления и малого быстродействия ПМК при посадке корабля может сложиться впечатление, что программа зацикливается. У пилота возникает искушение остановить программу с пульта (С/П), скомандовать В/О С/П и продолжить вычисления. Такие действия приводят к неправильному выходу из подпрограммы, стековая память адресов возврата засоряется, и происходит зацикливание. Подобная неприятность может случиться и в других программах, использующих вложенные друг в друга (наподобие матрешек) подпрограммы.

3. Избавиться от зацикливания в подпрограмме можно следующим образом: отдать с пульта команду С/П, а затем повторить несколько раз последовательность БП 92 ПП, пока не произойдет передача управления на адрес 01. После этого командой В/О С/П можно вновь запускать программу (вместо адреса 92 можно использовать любой другой, на котором записана команда В/О — в нашем случае 85).

Надо отметить, что не все читатели вели свои корабли к вершине по низкой окололунной орбите. Некоторые, «тряхнув стариной» (вспомнив предыдущее задание), совершили баллистический суборбитальный перелет, сэкономив на этом деле без малого две тонны топлива. Поскольку в задании ничего не говорилось о выходе на орбиту, это совершенно правильное решение.

О программе «Маскон» поговорим особо. Вероятно, целесообразно обсудить ее вместе с «Лунолетом-4». («Луна — это маскон! Маскон — концентрат массы в гравитационном поле планеты!.. Увеличь Землю до размеров лунной орбиты, тогда ты меня поймешь!»)

На «устные» задания тура удачнее всех, по нашему мнению, ответил восьмиклассник В. Ладохин из города Сургута Тюменской области, задержавшийся, кстати, на старте суборбитальных полетов: «Прошу меня извинить за то, что опоздал, просто калькулятор мне купили недавно». В ЦУП-«ТМ» причина признана уважительной. Начиная с задания № 2 В. Ладохин стал одним из наиболее дисциплинированных участников перелета.

Напомним заданные вопросы:

4) Прав ли был Коршунов, когда демонтировал 50 кг навигационной аппаратуры? Зачем он так поступил?

5) К какому приблизительно перерасходу топлива привела встреча «Кон-Тики» с масконом?

6) Видите ли вы какой-нибудь выход из сложившейся на «Кон-Тики» ситуации (кроме того, который предлагает Коршунов)?

А вот ответы Вадима:

4) Коршунов был прав. Так как лунолеты типа «Кон-Тики» не предназначены для орбитальных полетов, то и аппаратура у них была соответствующая. Поэтому при орбитальном, а тем более межпланетном полете большинство приборов «Кон-Тики» будет бесполезным грузом.

5) При встрече «Кон-Тики» с масконом перерасход топлива составил не более 5 кг.

6) Я думаю, что идти за борт никому не надо. Топлива на посадку хватит.

* * *

«По завершении рейса «Кон-Тики» хотелось бы увидеть в этом разделе новые игровые программы, — пишет девятиклассник Е. Бедекер (ст. Полетаев Челябинской области). — С их помощью, кроме удовольствия, полнее узнаешь возможности своего ПМК. Но вот еще было бы объяснение принципа составления и нюансов этих программ. Чтобы программа виделась осмысленным рядом действий, а не бездумным набором знаков. Чтобы с помощью вашего журнала научиться не только исполнять готовые программы, но и составлять их самому».

«С помощью МК-54 и программ, публикуемых в журнале, мы с другом совершили несколько увлекательных путешествий, — развивает похожую точку зрения 17-летний А. Дибривный из Херсона. — Нам бы хотелось совершить более сложные путешествия — к комете Галлея, к другим планетам Солнечной системы, к другим звездам, но мы не знаем, как составить программы для таких путешествий. Не могли бы вы рассказать, как можно составить такие программы, помочь нам в их составлении?»

«Я не думал о ПМК, но благодаря вашим публикациям попросил на день рождения именно программируемый, — сообщает не назвавший своего возраста Д. Евдокимов из Ленинграда. — В конце октября мне купили с трудом (дефицит почему-то!) МК-54. Теперь я осваиваю ваши программы. Спасибо вам за них! То, что вы придумали этот клуб, очень здорово! Но посвятите хотя бы один номер тому, как самому придумывать игры. Составить программу решения уравнения легко, а игру никак... Научите составлять игры!»

Что ж, пожелания законные, давайте придумаем игру вместе. По глубокому убеждению администрации, главное — это название. Назовем ее, скажем, «Многоступенчатая ракета». Ясно же, что на лунолете класса «Кон-Тики» далеко не улетишь, даже взлететь с Земли вряд ли удастся. Поставим задачу так: количество ступеней произвольно, после команды на отделение ступени задействуется следующая. Желательно, чтобы программа в обращении не была сложнее «Лунолета-3», который и возьмем за основу. Неплохо было бы сохранить и видеосообщения. Договоримся все постоянные и переменные величины оставить в прежних регистрах. Только теперь в регистре Д разместится запас топлива первой ступени, а в регистре 5, ясное дело, — ее «сухая» масса плюс полная масса всех последующих ступеней, включая полезную нагрузку.

Посмотрим, какие внутренние резервы есть у нашего «Лунолета-3». Команды, записанные по адресам 12–18, никакой роли не играют, просто повышают сервисность программы, рассчитывая и переводя в регистр Y круговую скорость на данной высоте. Это семь команд. Можно ли уместить сюда «многоступенчатый блок»?

Возьмем простейший случай. Пусть при зажигании двигателя каждой ступени полная масса ракеты распределяется поровну между следующими компонентами: 1) масса топлива нижней ступени; 2) масса ее конструкции; 3) масса всех последующих ступеней, включая полезную нагрузку. Легко видеть, что после команды на отделение ступени необходимо проделать следующие операции:

1) разделить оставшуюся массу ракеты (содержимое регистра 5) на 3;

2) полученное число записать в регистры 5 и Д;

3) вернуться на начало программы.

Наиболее простая последовательность команд, реализующая данный алгоритм, такова (адреса условные): 01.ИП5 02.3 03.÷ 04.П5 05.ПД 06.БП 07.00. Уложились ровно в семь команд! Блок сконструирован, но куда его вставить? И каким образом, не усложняя работы с программой, отдавать команду на разделение ступеней???

Обратим внимание на блок-схему, на то место, где производится проверка на перерасход топлива. Если вы внимательно следите за «топливными ресурсами», она бесполезна. Что, если команду с перерасходом сделать сигналом на отделение ступени? Значит, надо сделать так, чтобы при перерасходе управление перешло на только что сконструированный «блок многоступенчатости»!

Тот, кто хочет внести необходимые исправления сам, может «приглушить звук». Для остальных сообщаем алгоритм преобразования «Лунолета-3» в «Многоступенчатую ракету»:

1) Выбросить из программы команды по адресам 12–18;

2) Команды по адресам 19–26 «сдвинуть» вверх. Теперь они будут занимать адреса 12–19.

3) Вписать на адреса 20–21 команды 20.Fx<0 21.29.

4) Вписать на адреса 22–28 только что сконструированный «блок многоступенчатости».

Ракета построена. Вводите видеосообщения, нужные вам исходные данные, заливайте в баки горючее, определите себе цели полета — и в путь! Только администрация настоятельно рекомендует: внимательно следите за содержимым регистра 5. Ведь это масса всех пока еще бездействующих ступеней, включая полезную нагрузку. Не забывайте, что в нее входите и вы сами! И если команда ИП5 на очередном останове выдаст на индикатор, скажем, число 100, администрация обоснованно опасается, что вам, увы, уже ничто не поможет...

«Недавно просматривал ваш журнал № 10 за 1985 год, в частности рубрику «Клуб электронных игр», и возникло желание спросить: почему сообщение микрокалькуляторов типа Б3-34 и МК-54 по ошибке ERROR на страницах вашего (впрочем, не только вашего) журнала печатается в виде ЕГГОГ? — справедливо недоумевает А. Федоренко из Новосибирска. — Если это результат стремления избежать дополнительных трудностей при наборе, то оправдано ли такое стремление, в результате которого вместо осмысленного и понятного (по крайней мере, переводимого) слова появляется какой-то птичий набор?»

Отвечаем по существу. Для нас и наших читателей ЕГГОГ в первую очередь это: 1) условное обозначение чисел с порядками между 100 и 200 (см. № 1 с. г.), которые можно, например, записывать в регистры, отдавать по ним команды косвенной адресации (об этом еще расскажем) и т. д.; 2) своеобразное «прикрытие», пользуясь которым можно вызывать в регистр X и подвергать различным операциям числа, которые иначе вызвать не удается, скажем Тьму (№ 3); 3) универсальное «сырье», из которого можно получать такие полезные продукты, как символы Е, Г, С, L и -. Даже язык как-то не поворачивается назвать столь бесценное сокровище «ошибкой», пусть даже на английском языке...

Кстати, насчет символов Е, Г и т. д. «Почему вы написали, что после адреса 99 идут (в Б3-34) адреса А0...А9, В0...В9, С0...С9, Д0...Д9, Е0...Е9, 0... 9? — просит разъяснений заинтересовавшийся проблемой 160-шагового цикла А. Коротков из Тулы. — У меня они идут в следующем порядке: -0...-9, L0...L9, С0...С9, Г0...Г9, Е0...Е9,  0... 9. А «темная зона» начинается с адреса С3, а не С1, как сказано у вас».

Охотно даем разъяснения. Во-первых, символы -, L и Г есть соответственно коды букв А, В и Д, так что никакого противоречия в первом обнаруженном факте нет. Кстати, странички нашего клуба (или стены?) пронумерованы именно этими кодами. Второе замечание справедливо — «темная зона» начинается не с адреса С1 (что было бы странно!), а с адреса С0. При переходе же на адрес С2 она сплошь заполняет индикатор.

Наконец, сообщение, которое, несомненно, порадует всех любителей, если можно так выразиться, «компьютерной грамматики». Буквально накануне отправки номера в производство администрация КЭИ получила сенсационную телефонограмму следующего содержания:

«Извещаю, что мною получен простой способ формирования на Б3-34 любых комбинаций из цифр и символов Е, Г, С, L, -, не начинающихся с 0. Для этого нужно ввести в ПМК следующую программу: 00.КИП0 01.ВП 02.7 03.П9 04.КИП9 05.КИПЕ 06.ИП9 07.XY 08.XY 09.ВП 10.ВП 11.1 12./-/ 13.FL0 14.03 15.С/П.

(Е по адресу 05 означает стрелку вверх. — М. П.)

После ввода программы нужно сформировать и ввести в регистры 1, 2 и т. д. вплоть до 8 необходимые символы в том же порядке, в каком они входят в состав необходимого слова. Например, если вы хотите получить на индикаторе «слово» Г0-Г0-Г0, нужно ввести букву Г в регистры 1, 4 и 7, обнулить регистры 2, 5 и 8, ввести символ «-» в регистры 3 и 6. В регистр 0 заносится число букв в слове, не считая замыкающих его нулей, плюс один. В нашем случае 8. Теперь В/О С/П. Через десяток секунд на индикаторе появляется заказанное вами слово (с точностью до положения десятичной точки, но она легко переносится с помощью команды ВП).

Сообщаю также, что мною сконструирован инструмент для программного получения символов Е, Г, С, L и -. Вот соответствующая программа: 00.↑ 01.Сх 02.XY 03.XY 04.ВП 05.С/П. (По адресу 00 вписана стрелка вверх.) Если подать на ее вход цифру 9, после останова получим -. Если -, то L. Букву Е лучше не вводить — она дает «пустышку», а это символ весьма опасный.

В. Архипов».

Администрация КЭИ объявляет Владимиру Архипову благодарность и в этой связи дает следующее задание:

1) Получить максимальное число осмысленных слов и прислать их.

2) Придумать, каким образом, несмотря на категорическое утверждение нашего постоянного корреспондента, можно зафиксировать на индикаторе и записать в адресуемые регистры, скажем, названия программ «ОС-1», «ОС-2», «ОС-3».

Михаил ПУХОВ

АЛГОРИТМИЧЕСКАЯ ГИМНАСТИКА

ПРОГРАММА С ПРИПЕВОМ

Как печатают текст какой-нибудь песни? Сначала первый куплет, потом припев, потом второй куплет, а потом... лишь одно слово — «припев». Точно так же и после третьего куплета, если он, конечно, есть и т. д. В самом деле, зачем несколько раз печатать одни и те же строчки, когда достаточно указать, лишь где их нужно исполнять.

Аналогичная ситуация встречается и в программировании. Например, решая системы дифференциальных уравнений, приходится неоднократно вычислять правые части уравнений, при этом алгебраические формулы одни и те же, изменяются лишь значения входящих в них переменных. Конечно, нецелесообразно в такой задаче многократно выписывать в программе одно и то же. Специалисты давно придумали способ составления программ с «припевом». Повторяющаяся часть программы записывается только один раз в виде отдельного блока, которому присваивают собственное имя (набор цифровых или буквенных символов), чтобы его можно было отличить от других. Такие блоки носят название подпрограмм. Теперь, когда требуется обратиться к подпрограмме, то в тексте основной программы ставится специальный оператор вызова подпрограммы, вслед за которым указывается ее имя.

После того как мы познакомились с понятием подпрограммы, пора открыть небольшой «секрет» — возможно, что многие члены КЭИ оказались в положении мольеровского Журдена, который говорил прозой, не зная, что он говорит прозой. Ведь мы уже давным-давно использовали подпрограммы, путешествуя на «Кон-Тики» вместе с Лунным Коршуном. Чтобы убедиться в этом, обратимся к блок-схеме, «орбитальной» программы. Прежде всего о физической стороне задачи. Мы рассматриваем полет ракетного летательного аппарата по орбите вокруг безатмосферной планеты. При этом, кроме тяги двигателя и притяжения небесного тела, на лунолет действуют центробежная и кориолисова силы, дающие вклад в вертикальное и горизонтальное ускорения соответственно.

Ну а теперь пора «запевать песню», то есть проследить по блок-схеме работу программы. Сначала вводятся исходные данные, необходимые для совершения полета, — характеристики планеты и аппарата, начальные значения переменных. Затем вычислительная система определяет начальную высоту, так как в уравнениях движения в качестве текущей переменной выбрано расстояние от центра планеты. Далее идет уже знакомый нашим читателям по предыдущему выпуску рубрики блок проверки положительности высоты. Основную роль он играет при дальнейших маневрах, а сейчас мы просто выходим из ромба по стрелке «да» — ведь не искать же полезные ископаемые в недрах планеты мы собрались? И наконец, беремся за рычаги управления — вводим значения расхода топлива, угла тяги и время маневра.

Но прежде чем начать полет, бортовой компьютер проверит, не перерасходуем ли мы топливо. Если все в порядке — выход из блока проверки по стрелке «да», то приступает к работе блок вычисления реактивного ускорения. Он действует аналогично такому же блоку в программе «Лунолет-2» (см. «ТМ» № 5 за 1986 год). Кроме ускорения, этот же блок подсчитывает и запас оставшегося топлива. Итак, «куплет пропет», переходим к «припеву», — обращаемся к подпрограмме, которая определяет значения текущих переменных.

Несколько слов о ее работе. В первую очередь вычисляются составляющие ускорения — вертикальная и горизонтальная. Первая определяется проекцией реактивного ускорения на вертикаль, гравитационным ускорением, которое в нашем случае может быть переменным (так как меняется радиус орбиты), и центробежным ускорением. Вторая — проекцией реактивного ускорения на горизонтальное направление и кориолисовым ускорением. При нахождении проекций скорости и значений текущих координат используются обычные формулы равноускоренного движения, которые при своей простоте обеспечивают достаточную точность для задач подобного типа.

После окончания «припева» мы возвращаемся в основную программу и снова проверяем положительность высоты. Если полет проходит в нормальных условиях (выход из блока проверки по стрелке «да»), то опять беремся за рычаги управления и еще раз повторяем «куплет — припев». Наша «песня» продолжается до тех пор, пока мы либо благополучно не завершим перелет, либо...

«Этот человек... Бёрст врезался в Луну», — писал Станислав Лем в одном из рассказов о пилоте Пирксе. Ну что ж, никто не гарантирован от неудачи, и в нашем полете возможна ситуация, когда неосторожный маневр приводит к тому, что лунолет оказывается погребенным в недрах планеты (из блока проверки высоты мы выходим по стрелке «нет»). Нужно извлечь его оттуда. Это мы уже делали в программе «Лунолет-2», но сейчас предлагаем вам еще один метод. Как и в предыдущем случае, «спасение утопающих» оказывается делом не их рук, а микрокалькулятора. Время неудачного маневра делится пополам, причем знак его оказывается совпадающим со знаком высоты — если высота отрицательна, то и время отрицательно. Потом происходит обращение к подпрограмме, в нее вводится полученное отрицательное время, и лунолет проводится по траектории назад, при этом находится новое значение высоты. Затем оно сравнивается с нулем. Если высота занулилась, а при ее вычислении заодно происходит ее округление, программа заканчивает свою работу, прилунение (удачное либо неудачное) завершено. Если же высота отлична от нуля, то бортовой компьютер продолжает трудиться: время вновь делится пополам, а так как его знак совпадает со знаком высоты, то с помощью подпрограммы продолжается либо «извлечение» аппарата из недр планеты, либо — аналогичное пошаговое снижение. Существенно, что на каждом шаге приходится обращаться к подпрограмме. Конечно, «песня», в которой постоянно много раз подряд повторяется только «припев», не слишком содержательна, но что поделать, винить в этом можно только себя: чем точнее произведен последний маневр, тем она короче. В конечном счете лунолет оказывается на поверхности планеты, но, увы, ваша заслуга в этом невелика.

На этом очередная «зарядка» заканчивается.

Сергей ВОЛКОВ,
инженер