| <<< «ТМ» 1986 №4 | «Техника-молодежи» 1986 №5, с.50-54 | «ТМ» 1986 №6 >>> |
КЛУБ ЭЛЕКТРОННЫХ ИГР

МЯГКОЙ ПОСАДКИ!
Рейс «Кон-Тики» успешно завершен — и наш Клуб, как видим, незамедлительно перебрался в новое помещение (оформленное, как обычно, художником Евгением Катышевым). Клубу не хватает пока только названия; к сожалению, ни одного дельного предложения по этому поводу в редакцию не поступало. Слово за вами, дорогие читатели!
В обширной почте раздела есть слой довольно-таки примечательный. «Я с огромным удовольствием путешествовал по космосу, летал вокруг Луны, но вдруг врезался в скалу, — жалуется восьмиклассник из Харькова В. Бородавин. — У меня забрали мой «корабль» (микрокалькулятор), и я лишился средств передвижения. А к другим «кораблям» ваше топливо (программы для Б3-34) не подходит. Убедительно прошу вместе с программами печатать и блок-схемы для них. Составлять программу для любой машины, имея под рукой блок-схему, раз в 20 проще, чем переводить с другого языка. Предлагаю печатать блок-схемы к новым программам и наверстывать упущенное, то есть печатать блок-схемы к старым... Глубоко уверен, что это очень обрадует многомиллионную аудиторию читателей журнала...».
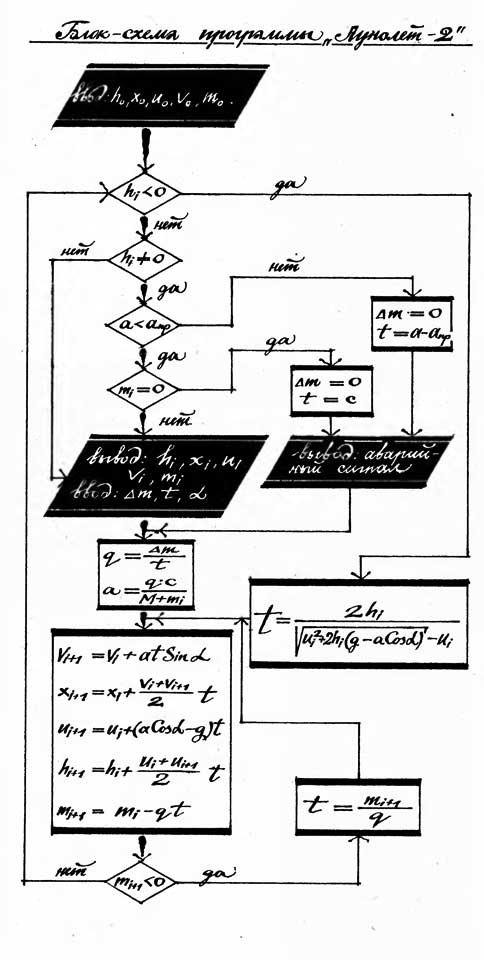
Аналогичные пожелания высказывают в своих письмах М. Клепиков из Киева, Н. Плеханов и Г. Красник из Москвы, В. Малинин из Новосибирска, В. Медноногов из Ленинграда, Е. Смирнов и С. Деревянко из Риги, Д. Грацилевский из Мурманска, А. Богуславский из Коломны, В. Голутвин из Львова, Л. Даймис из Свердловска, В. Туманов из поселка Байкит Красноярского края и многие другие. Учащиеся, преподаватели, конструкторы самодельных ЭВМ, программисты-профессионалы... Это в основном те, кто хочет переводить публикуемые в «ТМ» программы на языки персональных компьютеров. Что ж, требование вполне разумное, с удовольствием идем навстречу. Для начала, вместе с обзором ответов на задание первого этапа публикуем блок-схему игровой программы «Лунолет-2» (см. «ТМ» № 8 за 1985 год): в математическом смысле она проще последующих, зато всяких проверок и коррекций здесь значительно больше. Буквами обозначены константы: g — ускорение силы тяжести, M — «сухая» масса корабля, c — скорость истечения продуктов сгорания, aпр — предельное ускорение, которое может выдержать экипаж; основные переменные: h — высота; x — расстояние, u — вертикальная скорость, v — горизонтальная скорость, m — текущий запас топлива; управляющие параметры: α — угол тяги, t — время маневра, Δm — расход топлива за маневр. Из блок-схемы видно, что в программе вычисляются и используются также вспомогательные переменные: q — дифференциальный расход топлива (расход в единицу времени), a — реактивное ускорение. Индексом i помечены переменные на i-ом шаге игры.
Тех, кто интересуется алгоритмами вообще и данным алгоритмом в частности, отсылаем к нашей новой рубрике «Алгоритмическая гимнастика» (с. 48), также организованной в соответствии с вашими пожеланиями. Прежде чем перейти к обзору ответов на первое задание (см. «ТМ» № 8 за 1985 год), необходимо отметить творческий подход читателей, приславших свои варианты «Лунолетов». Например, С. Бердников из Новосибирска задает в качестве управляющего параметра непосредственно реактивное ускорение; такой ввод может оказаться особенно полезным при постановке игры на персональном компьютере в натуральном масштабе времени. И. Пшенко из Кривого Рога использует одинаковые по виду формулы для расчета вертикальной скорости и в основном счетном блоке, и в блоке коррекции высоты. Наконец, в программе В. Архипова из Москвы, рассчитывающей вертикальную посадку, добавляется принципиально новый игровой момент: нагрев корабля из-за аэродинамического торможения. Если подобный «тепловой блок» вставить в программу типа «Атмосферы-2» и ввести соответствующие температурные ограничения, игра станет гораздо реалистичнее и сложнее. В качестве базового видеосообщения В. Архипов использует число 11111111; умножая его на 2, 3 и т. д., легко получать новые наглядные сообщения. А сочетая этот прием с делением на 10 в нужной степени, можно моделировать на индикаторе ПМК стрелочные приборы: в этом случае, например, число 2222,2222 будет означать «стрелка на середине шкалы № 2» (допустим, израсходована половина топлива).
Первыми правильные ответы на задания первого этапа прислали В. Алексеев (Москва), В. Еженков (г. Дзержинск Горьковской области), Д. Журавлев, А. Долгалло (оба — Ленинград), А. Артамонов (г. Апрелевка Московской области), А. Морев (г. Устинов). Надо, правда, учитывать, что, как выяснилось при анализе ответов, августовский номер «ТМ» попал к некоторым подписчикам только в конце сентября! По первому вопросу («Какими физическими соображениями можно объяснить утверждение А. Перепелкина, что на Луне все ходят замедленно — сказывается меньшая сила тяжести?») мнение читателей практически единодушно. «Ходьба состоит из ряда «падений» то на левую, то на правую ногу. Чем меньше сила тяжести, тем медленнее будут происходить эти «падения» и темп ходьбы будет ниже. Кроме того, при малой силе тяжести довольно резкие движения при быстрой ходьбе могут привести к скольжению, так как сила трения уменьшится», — пишет, например, В. Шилов из Ярославля, и большинство читателей, придерживается аналогичной точки зрения, подкрепляя ее соответствующими математическими выкладками. Осторожнее высказывается А. Колосов из села Пышуг Костромской области: «Насчет того, ходят ли замедленно люди, точно не скажу (хотя астронавты, побывавшие на Луне, ходили не спеша, осторожно, медленно), а вот насчет, например, маятника можно сказать точно: чем меньше ускорение свободного падения на планете, тем медленнее он колеблется». Лишь один Л. Роканиди из Сызрани не согласен с утверждением А. Перепелкина. «Увлекшись математическими моделями лунной походки, — пишет он после довольно продолжительной дискуссии с администрацией КЭИ, — мы с вами забыли одну деталь: человек не ходит на прямых ногах. Поэтому амплитуда колебаний центра тяжести значительно меньше 4 см. Более того, можно ходить, вовсе не меняя его высоты. Лунная походка (которую, кстати, давно освоили в некоторых странах местные жители, переносящие тяжести на голове) действительно весьма грациозна, но нисколько не замедлена. В этом вопросе «человек из будущего» ошибается...» Но это мнение, повторяем, единично.
Консультант раздела —
Герой Советского Союза,
летчик-космонавт СССР
Ю. Н. ГЛАЗКОВ
Второе задание — определить ускорение силы тяжести способом зависания и по методу Лунного Коршуна — особых затруднений не вызвало. Способ зависания многие модифицировали: добивались в своих вариантах не зануления вертикальной скорости, а ее постоянства. Можно выделить решение М. Точина из Вологды — заменив команду 43.ИПА на 43.ИП3, он переоборудовал «Лунолет-1» таким образом, чтобы при останове на индикаторе зажигалась не высота, а более важная для данной задачи величина — реактивное ускорение. Наконец, весьма остроумный способ борьбы с кофейным автоматом (затмивший, на наш взгляд, метод Лунного Коршуна) придумали независимо друг от друга Ю. Кузнецов из Куйбышева и уже знакомый нам Л. Роканиди. Они использовали то обстоятельство, что полное ускорение корабля равно, с одной стороны, разности реактивного ускорения и ускорения свободного падения, а с другой — разности скоростей за время в 1 с. Вот соответствующая последовательность команд (выполняется в любой момент полета): ИПВ П0 1 ПП 1 С/П ИПВ ИП0 - ИП3 -. На индикаторе — искомое ускорение силы тяжести с точностью до последнего знака (а на столе — семь чашек ароматного кофе)! Отметим еще, что некоторые читатели слишком серьезно отнеслись к указанию из № 6 («Оставив рычаг расхода на прежней отметке, я рванул второй вниз до упора — 0,7 с...»). Естественно, при таком ограничении на время маневра метод Лунного Коршуна не проходит; очевидно, на злосчастном «одноруком бандите» подобного ограничителя не стояло.
Наиболее трудным заданием первого этапа, как и предполагалось, оказался тренировочный суборбитальный полет на «Лунолете-2» (напомним комплект исходных данных: 1,62 П4 2250 П5 3660 П6 29,43 П7 0 ПА ПВ П0 1 ВП 3 ПД 25 ВП 4 ПС. в регистре 9 — аварийный сигнал). «Я никак не мог с ним справиться, — пишет, например, Н. Плотников из Мончегорска. Мурманской области. — Самое большее, сколько я «пролетел», работая с этой программой, это 150 км... Напишите, пожалуйста, как разогнать и на какую высоту поднять «Кон-Тики», чтобы на 1000 кг горючего пролететь 250 км». Н. Плотников не одинок — с этой задачей не справились многие (В. Никифоров из Казани даже решил, что в условиях опечатка — расстояние до цели «равно не 250 км. а 25 км»). Она, кстати, была сформулирована не совсем четко, и некоторые читатели выполняли перелет «в одиночку», с сухой массой корабля 2150 кг (2000 + 150); такие решения тоже засчитывались. Но решить задачу при 2250 кг, конечно, гораздо сложнее.
«Этот вариант получился у меня не сразу, — честно признается один из победителей первого этапа. В. Алексеев, — недолеты составляли от 50 до 1,5 км. Возникла необходимость экспериментально подбирать время сгорания топлива при разгоне с точностью до 0,1 с. Ход полета: разгон, по возможности вертикальная и горизонтальная скорости должны быть равны, свободный полет, торможение с замедлением, равным ускорению при взлете, начало его приурочено к высоте начала свободного полета». Приводим последовательность команд В. Алексеева (номер маневра: расход/время/угол, в скобках — показание индикатора) с нашими комментариями. Надеемся, это поможет тем, кто не справился с заданием. Кроме того, она может служить и проверочным тестом к программе «Лунолет-2».
1: 100/3,9/42,5 (149,58601). 2: 100/4/42,5 (614,79833). 3: 100/4,1/42,5 (1421,7236). 4: 100/4,3/42,5 (2625,637). 5: 100/4,4/42,5 (4236,0811). 6: 35/1,6/43 (4916,9209). Разгон в основном закончен, реактивное ускорение все время выдерживалось максимально близко к предельному. Угол 42,5° выбран, чтобы скомпенсировать действие силы тяжести — вертикальная и горизонтальная скорости сейчас примерно равны; впрочем, практика показывает, что «классический» угол 45° ничем не хуже. 7: 2/1/88 (5357,4207). Очевидно, коррекция недолета, получившегося в предыдущей попытке, 8: 0/543,8/0 (4954,3996). После прохождения пассивного участка лунолет оказывается в симметричной точке траектории: расстояние до финиша примерно равно расстоянию от старта в конце разгона, высота приблизительно та же. Теперь начинается интенсивное торможение. 9: 100/4,6/-42 (3138,2379). 10: 100/4,8/-42 (1696,9962). 11: 100/5/-42 (686,8254). 12: 100/5,2/-43 (163,11224). Наиболее ответственный участок пройден. Скорость снижена на порядок, до финиша по прямой осталось примерно 200 м. Можно сбавить темп торможения и выходить к цели. 13: 20/2,2/-44 (75,41972). 14: 20/2,2/-45 (29,758463). 15: 10/2/-42 (15,983541). Лунолет в 16 м над целью, скорость погашена, начинается этап ювелирного прилунения. 16: 5/5/-3 (3,300477). 17: 2/1/1 (1,5622851). 18: 2/1,5/0 (0,7819925). 19: 2/2/0 (0,563843). 20: 1/2/-2 (0). Мастерская посадка! Отклонение практически равно нулю, горизонтальная скорость тоже, вертикальная составила около метра в секунду, а в баках осталось еще полтора килограмма топлива!
В данном случае пилота на финише заботило одно: установить мировой рекорд, прилунившись с точностью менее одного миллиметра (кстати, В. Алексеев после столь же успешно выполненного задания второго этапа был приглашен в КЭИ испытателем поступающих в редакцию игровых программ и в дальнейших полетах участия не принимал — не было времени). В том, что иногда ситуация складывается куда драматичнее, убеждает вариант П. Трубаева из Белгорода (показания индикатора для экономии места не приводятся).
1: 104/4/45. 2: 101/4/45. 3: 97/4/45. 4: 94/4/45. 5: 91/4/45. 6: 48,8/3/45. Как видим, разгон выполнялся под углом 45°, а топлива израсходовано даже на килограмм меньше, чем у Алексеева. Посмотрим, каковы будут результаты. 7: 0/520,8/0. Точный выход в симметричную точку. Но чрезмерная точность пилота подвела. Если бы он начал торможение всего на десятую долю секунды раньше, финиш скорее всего происходил бы примерно как в предыдущем варианте. 8: 48/3/-45. 9: 85/4/-45. 10: 82,3/4/-45. 11: 79,6/4/-45. Пилот с завидным хладнокровием повторяет в обратном порядке свои действия при разгоне, но ускорения чуть-чуть отличаются; вот это «чуть-чуть» его и подводит. 12: 77,7/4/-45. 13: 37/2/-45. В последний момент выясняется, что при планировавшейся команде 13: 74/4/-45, которая по идее должна была вывести корабль на финиш с солидной экономией топлива, лунолет — действительно рядом с финишем — разбивается вдребезги! Не хватает каких-то долей секунды. Поэтому П. Трубаев вдвое уменьшает время маневра, идя на прежнем режиме. В результате ситуация становится критической — до удара меньше секунды; что делать? 14: 24/1,3/0. Естественное решение: пилот над самой целью гасит вертикальную скорость, переходя в горизонтальный полет. И его, конечно же, уносит за точку финиша. Если бы, кстати, он тормознул сейчас не по вертикали, а с углом -15 или даже -20°, все проблемы были бы решены. Но посмотрим за его дальнейшими действиями. 15: 30/1,7/-80. Вот это да! Большинство, конечно, махнуло бы на все рукой и выполнило посадку метрах в пятидесяти от намеченной точки. Трубаев же подтверждает свою только что заработанную репутацию лихого пилота: истрачено почти все топливо, а лунолет по плавной параболе возвращается к финишу. 16: 0/4/0. 17: 0,6/0,6/30. Последняя капля горючего! 18: 0/1/0. Посадка! Она, правда, получилась слегка жестковатой, но, надо думать, амортизаторы выдержали. Зато не придется топать пешком по серым лунным камням...
Нельзя не остановиться и еще на одном рекордном варианте. А. Аула из Запорожья, выполнивший сначала перелет на корабле массой 2150 кг, узнав, что это не совсем то, решил блеснуть: совершил перелет еще раз, теперь уже при массе 2300 кг! Вот его вариант (только не забудьте изменить содержимое регистра 5: 2300 П5).
1: 4/1/0. 2: 53/2/45. 3: 52/2/45. 4: 51/2/45. 5: 100/4/45. 6: 97/4/45. 7: 94/4/45. 8: 91/4/45. 9: 3/0,2/45. 10: 0/524/0. 11: 87/4/-45. 12: 84/4/-45. 13: 83/4/-45. 14: 80/4/-45. 15: 77/4/-45. 16: 35/2/-45. 17: 2/1/0. 18: 6,2/0,5/-45. 19: 0,8/0,8/0. Отклонение от цели — меньше полуметра, полная посадочная скорость не превышает 2,4 м/с. Рекорд зарегистрирован и внесен в соответствующую книгу. Если есть желающие побить — милости просим!
«Я купил микрокалькулятор «Электроника Б3-34» всего три месяца назад, но благодаря КЭИ и подобным рубрикам в других журналах уже умею неплохо пользоваться ПМК, — пишет А. Сорокин из Кургана. — Все наиболее интересные программы, какие я нахожу в журналах, выписываю в общую тетрадь. Там набралось уже около 40 различных программ, из них почти 20 игровых. Благодаря вашим публикациям я могу теперь использовать ПМК на занятиях. Он стал моим первым помощником. Очень нравится «космический» цикл игровых программ, публикуемый в журнале. Конечно, еще не все получается так, как это нужно для нормального полета. Но с каждым разом я «летаю» все лучше. Хотелось бы, чтобы для разнообразия в журнале появлялись и «земные» программы...»
Подобные пожелания в нашей почте нередки. Стоит сразу определиться: мы публикуем и собираемся публиковать в первую очередь такие игры для ПМК, которые наиболее перспективны в смысле их перевода (с соответствующими дополнениями) на языки персональных компьютеров. К сожалению, абсолютное большинство присылаемых в КЭИ программ реализует несколько общеизвестных игр с простыми выигрышными стратегиями: игра Баше, «Ним» и их разновидности, «Угадай число», «Крестики-нолики», а также простейшие имитационные ситуации типа стрельбы из пушки. Алгоритмы этого рода задач (как правило, далеко не полностью использующих достаточно богатые возможности Б3-34) довольно подробно рассмотрены в книге Я. Трохименко и Ф. Любича «Микрокалькулятор, ваш ход!» (М., «Радио и связь», 1985). По-настоящему интересные программы почта приносит значительно реже. Наиболее оригинальные из них прислали
Д. Кайков из Белгорода, Ю. Пшенник из Харькова, В. Лозовой из Армавира, В. Архипов из Москвы, Г. Горовой из Керчи. Все это вполне «земные» игры, постараемся поместить их в ближайших выпусках КЭИ.
Начатая в январском номере «охота на инопланетных чудовищ» воодушевила многих читателей на дерзкие вылазки в глубины «электронного океана». Восьмиклассник С. Парамонов из Москвы самостоятельно (еще до выхода февральского номера) сконструировал простейшую «водолазную» программу (возведение в восьмую степень, запись результата в регистр, очистка стека) и поймал Тьму, подавая на вход ЕГГОГи, равные квадратам чисел от 1 ВП 94 до 1 ВП 99. Легко видеть, что его Тьма обитает на глубинах от 1500 до 1600, ровно на 1000 глубже обычной. Если попробовать записать ее в виде единицы с нулями, то она займет почти целый журнальный столбец! Независимо друг от друга В. Соболев из Усть-Каменогорска, С. Козинцев из Кременчуга и С. Банников из Москвы очутились в области «длинных монстров» (теперь уже знакомых нам по прошлому выпуску). В. Соболева, учащегося техникума, случайно завела в этот неисследованный район его программа (он работал на МК-61); однако он, в отличие от очевидцев Несси и «Великого морского змея», при встрече с неизвестным животным нисколько не растерялся и, открыв по нему беглый огонь из всех «бортовых орудий», в том числе и «снарядами главного калибра» (отсутствующими на клавиатуре Б3-34 командами выделения целой и дробной частей), получил интересные результаты в области новых видеосообщений, рассказать о которых придется несколько позже, когда будет обобщен опыт читателей, работавших в данном направлении (МК-61 в распоряжении редакции пока нет). Козинцев же и Банников (оба, кстати, учатся в восьмом классе) прорвались в запретную зону совершенно сознательно, воспользовавшись путем «снизу» (со стороны чисел с отрицательными порядками) и отважно перемахнув «вплавь» (в режиме АВТ) через обширные владения машинного Ноля. Вот как они плыли: 0,01 (количество нулей после запятой может быть произвольным) ВП /-/ 99 Fx2. На индикаторе — «длинный монстр» (80,10000000 9), а высказанное в № 1 категорическое утверждение (за пределы Тьмы, дескать, можно проникнуть лишь с помощью специальных программ) полностью опровергнуто!
С. Банников, кроме того, самостоятельно изучил Тьму (она, по его наблюдениям, представляет собой «нечто вроде джинна, которого надо держать в бутылке»), использовал ее (путем деления на 10200) для вычисления факториалов чисел в интервале от 253 до 293, а главное — открыл способ, который позволяет, не прибегая к помощи коварных чудовищ 4-го этажа, записывать в программу коды, начинающиеся с пустышки. (Это и есть тот «хитрый» прием, что был обещан в № 2.)
Скомандуйте, допустим, В/О КПП8. Калькулятор самопроизвольно переходит в режим ПРГ. Убираем точку — F ПРГ. Слева на индикаторе горит 8, справа — 39. Значит, мы, вслед за Сергеем, ухитрились вписать в программу совершенно новую команду (с кодом «пусто-8»), которой нет ни в одном руководстве по ПМК!
Точно таким же способом можно «изготовить» остальные команды с кодами «пусто-цифра». Правда, при использовании регистров от 0 до 6 результат зависит от их содержимого; например, если число в регистре 0 заканчивается на 1 или 2, команда В/О КПП0 дает желаемый результат (на адрес 30 вписывается «пусто-0»; похоже, кстати, на код команды FВх, но только на первый взгляд — ноль и пустышка поменялись местами), в противном же случае на индикаторе появляется ЗГГОГ-мутант, «расшифровка» которого ни к чему хорошему не приводит. Легко проверить, что любая из этих новых команд в режиме счета по программе выполняет функции «пустой» (в некоторых случаях даже четче, чем КНОП, К1 и К2). Но главное — их коды можно использовать в качестве адресов перехода на последнюю десятку команд длинной побочной ветви 160-шагового цикла, о котором рассказывалось в № 2 за этот год. Других способов добраться до этих мест не существует (кроме довольно-таки утомительной «ходьбы пешком» — ШГ, ШГ в режиме ПРГ; именно так, кстати, совершил «кругосветное путешествие» по всему циклу восьмиклассник Д. Третьякович из Свердловска).
Например, сейчас в программу вписан код «пусто-8». Если рассматривать его как адрес, то ему соответствует на главной ветви адрес 46. Используем это обстоятельство. F АВТ БП 37 F ПРГ БП (теперь на адресах 37–38 расположилась команда безусловного перехода БП 8) F АВТ БП 46 F ПРГ С/П (эта команда, по идее, должна продублироваться и на адресе «пусто-8») F АВТ БП 37 С/П. После останова переходим в режим ПРГ. Справа горит 9 — мы попали куда хотели. Больше на индикаторе ничего нет — «темная зона».
Еще любопытнее получается, если с помощью, скажем, В/О КППА (или В, С, Д, Е — она же стрелка вверх) F ПРГ вписать в программную память код «пусто-буква» и попытаться использовать его в качестве адреса перехода (ШГ влево ШГ влево БП ШГ влево F АВТ С/П). Куда передастся управление? Для ответа на этот вопрос полезно предварительно расставить на адресах 48–52 подходящие «сети» (вписать туда команды С/П), а после останова перейти в режим ПРГ. Редакция честно предупреждает: результат будет весьма неожиданным.
Михаил ПУХОВ
АЛГОРИТМИЧЕСКАЯ ГИМНАСТИКА
ПРОГУЛКА ПО «ЛУНОЛЕТУ»
Вряд ли кто из читателей «ТМ» переходит улицу с закрытыми глазами. Обычно мы придерживаемся строго определенного правила — подойдя к краю тротуара, останавливаемся, смотрим влево, оцениваем обстановку, доходим до середины улицы, затем смотрим вправо и либо пропускаем транспорт, либо заканчиваем переход. Как скажет математик, мы действуем по вполне определенному алгоритму.
Сегодня это слово можно услышать в разговоре людей самых различных профессий. Но термин «алгоритм» вовсе не порождение XX века. Это просто трансформированное имя средневекового математика аль-Хорезми (в переводе — «из Хорезма»). Его книга об искусстве вычислений в десятичной позиционной системе счисления во многом способствовала распространению в Европе столь привычных нам цифр и методов счета. В средние века европейцы называли алгоритмом именно десятичную систему и правила арифметических действий в ней. Все математики того времени даже делились на две группы — абацистов, которые вели расчеты на абаке, и алгоритмиков, владевших приемами письменных вычислений.
С тех пор смысл слова «алгоритм» изменился. Сегодня мы так называем набор правил для решения той или иной задачи. Сформулировать их можно по-разному.
Очень удобно представление алгоритмов в виде блок-схем, на которых хорошо видны структура алгоритма и связи между его отдельными частями. Подобно тому, как географическая карта позволяет туристам и путешественникам ориентироваться на местности, так и блок-схема помогает программисту «прокладывать маршрут».
С этого номера Клуб электронных игр (КЭИ) начал печатать «карты для программистов», то есть блок-схемы. Давайте же воспользуемся одной из них и совершим «путешествие» по алгоритму программы «Лунолет-2». Надеемся, что оно облегчит нашим читателям работу над собственными программами.
Итак, обратимся к рисунку. В его верхней части мы видим блок ввода исходных данных — вертикальной и горизонтальной скоростей, запаса топлива и координат точки старта. Затем следует несколько проверочных блоков. Об их назначении и работе мы поговорим несколько позже, а сейчас перейдем к блокам вычисления текущих значений вспомогательных и основных переменных.
Прежде всего несколько слов о физической стороне задачи. На ракету, находящуюся в постоянном гравитационном поле при отсутствии атмосферы (а именно такая простейшая модель использована в программах «Лунолет-1» и «Лунолет-2»), действуют сила тяжести и тяга двигателя. Величина реактивного ускорения зависит от секундного расхода топлива, а направление определяется углом тяги. Этот угол вводится непосредственно (см. темный блок в середине рисунка). Кроме того, здесь же вводятся расход топлива на данном шаге и время, за которое он производится. После этого блок вычисления вспомогательных переменных определяет секундный расход и реактивное ускорение. Эти результаты передаются в блок вычисления текущих значений основных переменных.
Его задача — найти значения координат и скоростей после отработки двигателя. Так как ускорения постоянны, то используются хорошо знакомые из школьной физики формулы равноускоренного движения. Одновременно подсчитывается и количество оставшегося топлива.
Теперь, казалось бы, самое время выводить полученные величины на индикатор, но на рисунке путь к блоку вывода почему-то извилист и лежит через несколько проверок. В чем дело?
Действительно, игровые программы принципиально отличаются от обычных расчетных. Когда мы просто решаем уравнения, то действуем по принципу «куда прилетели, туда и прилетели». Вычислительная техника, неважно, компьютер или микрокалькулятор, подсчитывает координаты и скорости в конечной точке и выводит их на дисплей или индикатор. Нам остается только ознакомиться с результатами. В игровой же программе мы периодически вводим управляющее воздействие, в нашем случае — изменяем величину и направление реактивного ускорения. Но ведь это можно сделать не всегда. Если, скажем, ваш лунолет превратился в «землерой», то есть высота получилась отрицательной, дальнейшая игра бессмысленна. Чтобы выявить такого рода ситуации, в алгоритм и введены блоки проверок. Посмотрим же, как они работают.
Прежде всего выясним, сколько топлива осталось после маневра? Если запас окажется меньше нуля, значит, такой маневр невозможен, ведь летать на «отрицательном топливе» нельзя. Нужно вернуть лунолет в ту точку траектории, где кончилось горючее. Микрокалькулятор определяет, сколько секунд назад опустели баки, и передает это значение (отрицательное!) в блок вычисления основных переменных. Там оно подставляется в уравнения движения, и «бортовой компьютер» отводит наш летательный аппарат назад, по той же самой траектории, в точку, где иссякло топливо. Именно с ее координатами и соответствующими скоростями продолжает работать программа.
Следующей «становится на проверку» высота. Если она неотрицательна (выход из блока сравнения по стрелке «нет»), то все в порядке. Если же лунолет уже «забурился» в недра планеты, надо извлечь его оттуда. Как это сделать?
«Бортовой компьютер» исправляет ошибку пилота тем же методом, что и в случае перерасхода топлива. Подсчитывается время «полета» под поверхностью планеты, и его значение (опять-таки отрицательное) передается в блок вычисления основных переменных. Лунолет возвращается по траектории назад, в точку финиша. Блок вывода сообщает о том, где мы оказались (значение горизонтальной координаты) и насколько мягкой была посадка (величины скоростей). Если же высота еще положительна, то наступает черед следующей проверки — «биологической».
Из-за слишком большой перегрузки экипаж лунолета мог потерять сознание (выход по стрелке «нет»). В этом случае управление берет на себя автоматика — выводится аварийный сигнал, останавливается двигатель, и некоторое время полет происходит по инерции. Оно определяется разностью реактивного и предельно допустимого для пилотов ускорений, что достаточно разумно для игровых программ. Блоки вычисления переменных определяют, где окажется аппарат, когда экипаж вновь сможет «взять в руки штурвал». Если же перегрузки не превысили нормы, то мы выходим из блока сравнения по стрелке «да» на последнюю проверку: наличия топлива.
При пустых баках управление вновь передается бортовому компьютеру — он задает нулевой расход (ведь летать-то уже не на чем), большое (порядка тысяч секунд) время и передает эти данные в блок вычислений. Пилотам остается лишь созерцать аварийный сигнал и ждать, когда они «куда-нибудь свалятся» (по меткому выражению Лунного Коршуна). Если же топливо еще есть, то можно продолжать полет. ПМК «докладывает обстановку» и ждет очередной команды с пульта.
Приведенная блок-схема удобна для постановки игры на персональном компьютере, так как его возможности несравненно больше, чем у микрокалькулятора.
Первые шаги в этом направлении уже сделаны. «В соответствии с Основными направлениями реформы общеобразовательной школы исполнительный комитет Октябрьского районного Совета народных депутатов Тюменской области определил меры по обеспечению компьютерной грамотности учащихся средних школ района, — пишет в редакцию председатель исполкома А. М. Вахонин. — Постановлением Октябрьского районного комитета КПСС и Октябрьского райисполкома от 24 апреля 1985 года принято решение создать вычислительный центр в опорной Сергинской средней школе и серьезно оснастить его новейшими современными персональными компьютерами, выделив на это материальные средства от базовых предприятий, и считать этот центр учебно-методической базой в масштабе школ района по изучению методики преподавания основ информатики и вычислительной техники... В настоящее время создана лаборатория, где установлены две микро-ЭВМ ДЗ-28, дисплеи ИЭ-00-13, термопечатающее устройство... Машины работают по 9 часов в сутки, машинного времени, чтобы удовлетворить всех желающих, явно не хватает — мало машин. Интерес к вычислительной технике и программированию чрезвычайно высок.
Особенно заинтересовались дети статьями о фантастических электронных играх на космические темы, напечатанными в журнале «Техника-молодежи». Девятиклассники Латыпов Урал и Заволока Владимир, слушатели факультатива «Программирование на БЕЙСИКе», решили перенести все эти игры на машину ДЗ-28. Сейчас программа «Лунолет-1» переведена на язык БЕЙСИК. Программисты полностью разобрались в алгоритме, нарисовали блок-схемы. Программа получилась очень красивой, с интересными комментариями, объяснениями непонятных ситуаций, возникающих при взлете и посадке. Игра идет в виде урока, который ведет ЭВМ. Сейчас началась работа над «Лунолетом-2». В перспективе — все ваши интереснейшие программы перенести на микро-ЭВМ».
Мы ознакомились с программой тюменских школьников, любезно предоставленной руководителем юных программистов С. П. Митрофановым. Сделана она достаточно профессионально, кроме того, ребятам не откажешь в чувстве юмора. Так, при посадке со скоростью, превышающей 10 м/с, на дисплее появляется сообщение: «Я вас могу успокоить лишь тем, что по вас плачут родственники и друзья». Если же посадка была удачной, то компьютер «присваивает вам очередное звание» (вплоть до генерала) и предлагает совершить следующий полет в более сложных условиях. Кроме того, игра снабжена и комплексом предстартовых проверок, когда надо ответить на ряд несложных теоретических вопросов, касающихся будущего полета. Но здесь надо быть осторожным и внимательным. По крайней мере, представитель администрации КЭИ, заявивший, что выдерживает пятнадцатикратные перегрузки, немедленно был «снят с полета за хвастовство».
Персональный компьютер позволяет также вести игру в реальном масштабе времени. Это, конечно, приближает ее к действительности. Пока администрация КЭИ такими программами не располагает и надеется здесь на помощь читателей.
Сергей АЛЕКСЕЕВ,
инженер
| <<< «ТМ» 1986 №4 | «Техника-молодежи» 1986 №5, с.50-54 | «ТМ» 1986 №6 >>> |