1. Природа сил тяготения
2. Сила тяжести на земной поверхности
3. Поле тяготения в окрестностях земного шара
4. Поле тяготения вокруг других небесных светил
5. Работа, необходимая для преодаления силы тяжести
6. Параболическая и круговая скорости
7. Понятие об идеальном импульсе
8. Дальность действия силы тяжести.
9. Взаимно налагающиеся поля тяготения
10. Критическая точка. Граница Роша
Большинство авторов новейших романов, в которых описываются межпланетные путешествия, позволяют своим героям легко преодолевать земное притяжение. Чаще всего для этого придумывается какое-нибудь невесомое вещество, или же какое-нибудь средство, позволяющее освободиться от действия земного притяжения.
1. Природа сил тяготения
Мы до настоящего времени еще ничего не знаем ни о самой природе силы тяжести, ни о том, как, собственно говоря, эта сила действует. Поэтому мы вправе предполагать, что невесомые вещества, а также средства для преодоления земной тяжести, действительно могут быть изобретены. Здесь невольно приходит в голову сравнение с электромагнитом, теряющим свою силу, как только прекращается текущий по его обмоткам электрический ток. Однако маловероятно, чтобы в ближайшем будущем какие-либо производимые в этом направлении попытки привели нас к желаемой цели, потому что весь наш научный опыт говорит против такой возможности. До настоящего времени не только не оказалось возможным изменить, т.е. искусственным образом усилить или ослабить, действие силы притяжения какой-нибудь массы, но даже не удалось и отгородиться от действия этой силы. Световые и тепловые лучи, и даже лучи Рентгена, обладающие значительно большей пронизывающей силой, равно как и электрические волны и излучения радиоактивных элементов, могут быть задержаны соответственно подобранными веществами, помещенными на их пути. Одни лишь «лучи тяжести» до сих пор ни в чем еще не могли быть ни остановлены, ни задержаны. Земной шар пронизывается ими, по-видимому, без всякого затруднения. По крайней мере, все попытки установить во время полных лунных затмений поглощение «лучей тяжести» Солнца Землею, становящейся между Солнцем и Луною, были тщетны.
Поэтому приходится считать тяготение свойством столь же неизменно присущим всякой массе, как и инерцию. Такого взгляда мы должны придерживаться, как некоторого положения, установленного опытным путем, несмотря на то, что логически он нам может казаться весьма сомнительным. Мы вправе думать так, пока опять-таки опытом не будет доказано противное. Такое положение вещей, несомненно, весьма печально. Оно было бы совершенно безнадежно и нам пришлось бы отказаться от возможности когда-либо покинуть нашу Землю, если полет в мировое пространство смог бы быть осуществлен только при помощи какого-либо невесомого вещества или путем освобождения от действия силы тяжести. К счастью, в действительности это не так. Для наших целей будет совершенно достаточно преодолеть силу земного притяжения, противопоставив ей какую-либо другую, более мощную силу природы, соответственно направленную человеческой техникой. Здесь перед нами открываются даже не один, а несколько различных путей. Приведет ли нас, хотя бы один из них, к цели, т. е. сможем ли мы когда-нибудь на «корабле вселенной» порвать оковы земного притяжения? Об этом мы сможем судить, лишь основательным образом познакомившись с характером и прочностью невидимого панциря земного притяжения. Только тогда мы сможем подсчитать, какая сила необходима нам для того, чтобы пробить этот панцирь.
2. Сила тяжести на земной поверхности
На земной поверхности в нашей повседневной жизни мы знакомы с двумя проявлениями силы тяжести. Всякое свободное, ничем не поддерживаемое тело под действием этой силы падает к центру Земли, приобретая при этом так называемое ускорение свободного падения, Всякое же тело, свободное падение которого чем-либо задерживается, оказывает на свою подставку, или на другие препятствия, мешающие ему падать, некоторое давление, которое мы называем весом этого тела.
Мы говорим поэтому: на всякое тело, находящееся на земной поверхности, тяжесть действует как сила, направленная вертикально вниз. Величину этой силы мы можем измерить или силой производимого телом давления, или величиной ускорения падения (а также длиной пути, проходимого телом в первую секунду падения). В качестве единицы этой силы принимается давление, оказываемое на подставку платиново-иридиевой гарей, хранящейся в Международном бюро мер и весов в Севре, близ Парижа. Вес (G) этой гири равен ровно одному килограмму(кг). Если мы выдернули бы из под гири то, на чем она стоит, то она стала бы падать и к концу первой секунды пролетела бы 4,903325м, развив в этот момент вдвое большую скорость, а именно 9,80665 м/сек. Это последнее число называется ускорением силы тяжести (g) на земной поверхности. Оно выражает ежесекундное увеличение скорости свободно падающего тела под действием его притяжения к Земле.
Деля вес тела на ускорение силы тяжести в месте его нахождения, мы получаем массу этого тела М = G/g. В противоположность весу тела, меняющемуся в зависимости от господствующей силы поля тяготения, масса тела при всех его перемещениях в пространстве, равно как и при всех химических его превращениях и изменениях его физического состояния, всегда остается неизменной. В силу этого она является важнейшей постоянной величиной, характеризующей данное тело, и образует единственную пригодную основу для многих последующих рассуждений, единицей массы является килограмм-масса (кг+).
Так как в средней полосе СССР, расположенной сравнительно невысоко над уровнем моря, при соответствующей длине земного радиуса в 6371 км ускорение силы тяжести g=9,81 м/сек, то у нас тело будет обладать массой в 1 кг+ тогда, когда оно на обыкновенных весах будет весить 9,81 кг и, наоборот, тело весом в 1 000 кг будет обладать массой в 101,93 кг+.
Вот то, что мы можем узнать о нашем главном противнике, земной тяжести, оставаясь на поверхности Земли.
3. Поле тяготения в окрестностях земного шара
Иной вопрос, как изменится действие силы земного притяжения в том случае, если мы поднимемся над земной поверхностью, т.е. удалимся от центра Земли. Опыт учит нас, что вес всякого тела уменьшается по мере подъема его над поверхностью Земли. Гиря весом в 1 кг, будучи поднята над уровнем моря на 1000 м и положена там на чашку точных пружинных весов, произведет на нее давление в 999,25 г. Это уменьшение веса обусловливается законом распространения силы тяжести. Со времени Ньютона мы знаем, что напряжение поля тяготения вокруг каждой притягивающей массы убывает прямо пропорционально квадрату расстояния от центра этой массы.
Это значит: если мы положим радиус Земли равным 1 (в действительности он измеряется 6371 км) и силу тяжести на земной поверхности также равной 1, то величина этой силы на расстоянии 2 (земных радиусов) от центра Земли составит 1/4, на расстоянии 3 - только 1/9, на расстоянии 4 - всего лишь 1/16, на расстоянии 5 - уже только 1/25 и т.д. и, наконец, на расстоянии 10 - всего-навсего 1/100. На расстоянии 1 миллиона земных радиусов эта сила составит только 1 биллионную долю своей первоначальной величины, а на расстоянии миллиарда радиусов только одну триллионную* ее долю.
* Здесь, как и всюду в книге, автор называет миллионом 106=1 000 000, миллиардом 109 = 1 000 000 000, биллионом 1012 = 1 000 000 000 000 и триллионом 1018 = 1 000 000 000 000 000 000 (Прим. Ред.)
В таком же соотношении, разумеется, уменьшается и вес (кг) всякого тела, поднимаемого в пространстве, в то время как масса его (кг+) остается неизменной.
Наиболее наглядное представление об убывании силы тяжести по мере удаления от какого-нибудь небесного тела нам дает кривая тяготения (рис. 1). Она строится следующим образом: по горизонтальной оси координат откладываются расстояния, а по вертикальной - напряжения силы тяжести, и концы полученных отрезков соединяются плавной кривой. Лучше всего при этом радиус небесного тела - в данном случае Земли - и напряжение силы тяжести у его поверхности положить равными единице, потому что тогда будет удобно сравнивать между собой поля тяготения различных светил. В той же степени, в которой точки кривой но мере продвижения к правой стороне чертежа приближаются к горизонтальной оси координат, будет ослабевать и поле тяготения.
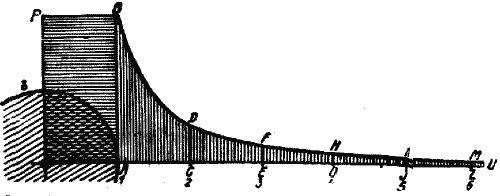
Рис.1. Кривая земного притяжения. На горизонтальной линии отложены расстояния от центра Земли в земных радиусах (1,2…5,6); высоты перпендикуляров АВ, CD, EF и т.д. служат мерою напряжения силы земного притяжения на соответственных расстояниях ОА, ОС, ОЕ и т. д. Вертикально заштрихованная площадь ABU ограниченная кривой, равновелика прямоугольнику АВРО. Земной шар, изображенный кружком с центром в точке О, отмечен значком Земли -
4. Поле тяготения вокруг других небесных светил
Закон Ньютона позволяет строить кривые тяготения не только для Земли, но и для других небесных светил, если только нам известны их диаметры и массы (или, вернее говоря, отношение их диаметров и их масс к диаметру и массе Земли). Так, например, мы получим кривую лунного тяготения, укоротив все ординаты кривой земного тяготения в 81 раз, т.е. построив кривую в 81 раз более плоскую по сравнению с последней. Правда, радиус Луны тоже меньше, благодаря чему ее поверхность находятся ближе к центру Луны, чем земная поверхность к центру Земли. В силу этого напряжение силы тяжести на Луне составляет не 1/81, а 1/6 земного притяжения на поверхности нашей планеты. Вместе с этим, разумеется, оказываются вшестеро уменьшенными и вес, и длина свободного падения в первую секунду, и ускорение силы тяжести по сравнению с тем, что мы видим у нас. Однако масса тел остается при этом совершенно неизменной. Окорок, захваченный на Луну, насытит нас там не меньше, чем на Земле, несмотря на то, что весить он будет в шесть раз меньше. Атлет же, перенесенный на Луну, сможет поднять там в шесть раз большую массу, потому что сила его мышц противопоставляется не массе, а весу тел. (Для других планет см. соответствующие значения, приведенные в таблице 1 данной главы).
Кроме того, для лучшего усвоения рекомендуется построить в крупном масштабе кривые тяготения для Венеры и для Марса, потому что достижение этих светил на кораблях вселенной после достижения Луны будет наиболее легким. Площади, заключенные между этими кривыми и осями координат, на которых они построены, будут служить мерой работы силы тяжести при удалении от светила. Эти площади будут равновелики прямоугольникам, высоты которых равны наивысшим ординатам, изображающим напряжение силы тяжести на поверхности планеты, а основания - радиусам этих светил. Величины этих площадей и будут характеризовать собой те работы, которые необходимы для того, чтобы пробить панцирь притяжения этих светил, а это именно нас и интересует (рис.2).

5. Работа, необходимая для преодоления силы тяжести
Работу, которую надо совершить, чтобы поднять 1 кг на 1 м, мы называем одним килограммометром. Если бы напряжение силы тяжести не убывало с высотою, то работа, необходимая для поднятия 1 кг на 1000 м, составляла бы 1 000 кгм. В действительности же она меньше в силу того, что в данном случае тяжесть уменьшается по закону Ньютона. Какая же работа необходима для того, чтобы удалить 1 кг из сферы земного притяжения (иными словами, в бесконечность)? Посмотрев на построенный чертеж, мы уясним себе, что эта работа будет равна той, которая потребовалась бы для поднятия 1 кг в неослабевающем поле земного притяжения на высоту одного радиуса Земли (6 371 км), т.е. у нас на Земле будет равна 6 371 000 кгм. Мы называем это число потенциалом или напряжением силы тяжести наземной поверхности.
Приняв силу, необходимую для поднятия какого-нибудь тела в бесконечность, за 1, мы сможем вычислить работу, необходимую для поднятия этого тела на любую высотуR из уравненияH=1 - (1/R), гдеR-расстояние наивысшей точки поднятия от центра светила, выраженное в его радиусах. Желая же сравнить, например, напряжение силы тяжести на других светилах с напряжением силы тяжести на Земле, мы сможем выполнить это путем подстановки соответствующих значений радиусов этих светил. Так, например, для Луны, радиус которой равен 2/7 земного, а напряжение силы тяжести на поверхности 1/6, мы найдем: 2/7 х 1/6 = 2/42 = 1/21. А для Юпитера мы получим: 11,19 х 2,54 = 28,4. Это значит, что пробить панцирь лунного притяжения в 21 раз легче, чем преодолеть тяготение земное, и что совершить последнее в свою очередь в 28,4 раза легче, чем преодолеть силу притяжения великана планетной системы Юпитера. Следовательно, покинуть Луну для возвращения на Землю во много раз легче, чем улететь с Земли с целью достигнуть Луны. Будущим кораблям вселенной придется особенно остерегаться Юпитера, чтобы не сделаться навеки его пленниками. Для поля тяготения Солнца мы совершенно таким же способом придем к ужасающему числу 3052. А несмотря на это, Земля наша благополучно вращается вокруг Солнца, на расстоянии 149,5 млн. км, вследствие чего поле тяготения Солнца, в окружающей Землю части пространства ничтожно мало. Ускорение силы тяжести по направлению к Солнцу равно у нас 5,9 мм/сек2, а камня по направлению к Земле 9 810 мм/cек2.
Для оценки возможностей произвести спуск на поверхности других планет и последующий подъем с них в пространство необходимо знать напряжения силы тяжести на их поверхностях, выраженные как в абсолютной мере (в килограммометрах), так и в относительных числах (принимая напряжение силы тяжести на земной поверхности за 1).
Поэтому мы приводим соответствующие значения в таблице 1.
6. Параболическая и круговая скорости
Выраженная в килограммометрах работа, необходимая для преодоления напряжения силы тяжести на поверхности какого-нибудь небесного тела, еще не дает нам достаточно наглядного представления для быстрой оценки необходимой мощности двигателей корабля вселенной, предназначенного для осуществления определенного маршрута в мировом пространстве. Для этого нам необходимо перейти к определению скорости, которую необходимо сообщить телу для того, чтобы оно могло вырваться из оков тяготения данного небесного тела. Мы называем эту скорость параболической потому, что в этом случае путь этого тела будет являться параболой. Вычисление этой скорости производится очень просто по закону, согласно которому разгон движущегося тела равен половине произведения его массы на квадрат его скорости. Эта зависимость выражается уравнением:
Разгон же движущегося тела есть не что иное, как его кинетическая энергия или живая сила, которая проявится тогда, когда равномерное его движение будет чем-нибудь замедлено или остановлено. По своей величине она равна той работе, которую необходимо затратить для того, чтобы это тело, первоначально находившееся в покое, привести в движение с той же самой скоростью. Так как масса, соответствующая весу в 1 кг, равна 0,102 кг+, то, производя подстановку в вышеприведенное уравнение, мы сразу же получим необходимую скорость, при которой кинетическая энергия этой массы становится равной значению силовой функции на земной поверхности*, т. е. 6 371 000 кгм. Мы получаем параболическую скоростьVр=11 181 м/сек.
* Иными словами, работе, которую необходимо затратить для удаления 1 кг на бесконечное расстояние от Земли. Эту же энергию приобретает тело при падении на Землю с бесконечно большого расстояния. (Прим. ред.)
Эта cкорость, будучи сообщена телу, окажется достаточной для того, чтобы освободить его из оков земной тяжести в том предположении, что сопротивление воздуха которое необходимо преодолеть, отсутствует. И наоборот, падающее из бесконечности тело в момент достижения им земли (в том же предположении) приобретет ту же скорость.
Зная, что параболическая скорость на нашей Земле равна 11 181 м/сек на уровне моря, мы без труда сможем вычислить ее величину для любой высоты над этим уровнем. Она будет* уменьшаться прямо пропорционально корню квадратному из расстояния от центра Земли. Таким образом на высоте в 1 600 км над уровнем моря параболическая скорость будет равна 10 000 м/сек, на расстоянии одного земного радиуса над уровнем моря - 7 906 м/сек, а на высоте трех земных радиусов или на расстоянии четырех радиусов от центра Земли она будет равна половине своего значения на уровне моря (11 181 м/сек), т.е. 5 590 м/сек.
* Согласно закону всемирного тяготения Ньютона. (Прим.Ред.)
Вычисление соответствующих параболических скоростей для поверхностей других небесных тел проще всего осуществляется следующим образом. Напряжение силы тяжести на поверхности этого небесного тела умножается на его диаметр и из полученного произведения извлекается квадратный корень; это соотношение выражается уравнением:
Подставляя в него относящиеся к Земле величины 9,81 х 12 742 и извлекая корень, мы получим опять-такиVр= 11 181 м/сек. Произведя соответствующие вычисления, мы убедимся в том, что параболическая скорость на поверхности Венеры равна 10 000 м/сек, на поверхности Марса - 5 030 м/сек, на поверхности Меркурия - 4 300 м/сек, на поверхности нашей Луны - 2 400 м/сек. На обоих спутниках Марса, Деймосе и Фобосе, и на наименьших из числа так называемых, малых планет или астероидов, диаметры которых измеряются несколькими километрами, параболическая скорость составляет всего лишь 20 - 25 м/сек; такой скорости может достигнуть уже брошенный рукою камень.
Деля параболическую скорость на число 1,414 мы получим соответствующую данному месту, так называемую, круговую скорость. Будучи сообщенной какому-нибудь телу, она заставит его обращаться точно по кругу около центра притяжения. На нашей Земле на уровне моря круговая скорость VR=7 906 м/сек.
При промежуточных скоростях (больших 7 906, по меньших 11 181 м/сек) будут получаться эллипсы. Двигаясь по одному из них, тело сначала будет подниматься от земной поверхности в пространство, но затем, пролетев наиболее удаленную точку этого эллипса, оно будет приближаться обратно к земной поверхности. Ввиду этого для вычисления необходимого запаса энергии в двигателях корабля вселенной, предназначенного для осуществления определенного маршрута в мировом пространство, нам нужно знать параболические и круговые скорости, приводимые в таблице 1.
Таблица 1
| Название | Экваториальный диаметр | Масса (Земля=1) | Напря- жение силы тяжести на поверх- ности ( | Высота падения в первую секунду | Сила притяжения | Скорость в км/ceк | Скорость обращения вокруг Солнца в км/сек | |||
| в км | пара- боли- ческая | круг- овая | круг- овая | пара- боли- ческая | ||||||
| Солнце | 109,05 | 1391000 | 333 432 | 28,04 | 137,1 | 3 053 | 623,00 | 430,00 | (Луна вокруг Земли) | |
| Луна | 0,273 | 3470 | 0,0123 | 0,16 | 0,8 | 0,044 | 2,39 | 1,69 | 1,02 | 1,44 |
| Меркурий | 0,380 | 4842 | 0,06 | 0,06 | 1,9 | 0,148 | 4,49 | 3,03 | 48,1 | 68,0 |
| Венера | 0,956 | 12191 | 0,82 | 0,82 | 4,4 | 0,950 | 10,00 | 7,07 | 35,2 | 49,8 |
| Земля | 1,000 | 12756 | 1,00 | 1,00 | 4,9 | 1,000 | 11,18 | 7,91 | 29,9 | 41,8 |
| Марс | 0,532 | 6784 | 0,11 | 0,38 | 1,9 | 0,202 | 5,03 | 3,54 | 25,9 | 36,7 |
| Юпитер | 11,19 | 142745 | 318,36 | 2,54 | 12,54 | 28,423 | 59,30 | 41,90 | 13,1 | 18,6 |
| Сатурн | 9,47 | 120780 | 95,22 | 1,06 | 5,2 | 10,038 | 35,50 | 25,10 | 9,67 | 13,7 |
| Уран | 3,90 | 49692 | 14,58 | 0,96 | 4,7 | 3,744 | 19,80 | 14,00 | 6,84 | 9,7 |
| Нептун | 4,15 | 53000 | 17,26 | 1,00 | 4,9 | 4,150 | 22,40 | 15,80 | 5,46 | 7,7 |
7. Понятие об идеальном импульсе
Проблема полетов в мировом пространстве в смысле теоретически необходимой затраты энергии для полного освобождения из оков земной тяжести сводится, в конечном счете, к постройке таких машин, которые, приводя в движение корабль вселенной, могли бы сообщить ему большую кинетическую энергию или большую живую силу полета, чем та, которая заключена в параболической скорости для данной планеты. Следовательно не мы, люди, были слишком слабы для того, чтобы подняться в мировое пространство, но сама Земля, как сравнительно крупное и массивное небесное тело, до сего времени была слишком сильна для наших технических средств, недостаточных по мощности для того, чтобы пробить панцирь земного тяготения.

а) в момент зажигания, b) при полусгоревшем заряде, с) в момент окончания горения заряда,
М0 - начальная масса, М1 - конечная масса, V0 - начальная скорость, V1 - конечная скорость, С - скорость извержения струи газов из ракеты.
Идеальный импульс V1 = С ln (М0/М1). Подробности см. главу 4 раздела II.
Для подъемов на относительно небольшие высоты в окрестностях нашей Земли будет достаточна значительно меньшая кинетическая энергия. Для перелетов же в пределах солнечной системы со спусками на другие планеты или спутники, повторными подъемами с них или с облетами вокруг них и другими маневрами, потребуется гораздо большее количество энергии, чем то, которое необходимо только для того, чтобы вырваться из оков земной тяжести (см. цифровую сводку в таблице 2).
В каждом отдельном случае запас энергии в корабле вселенной, необходимый для осуществления намеченного маршрута, может быть выражен одним числом, которое мы называем идеальным импульсом силы, или просто идеальным импульсом. Под этим названием мы подразумеваем ту идеальную конечную скорость, которую корабль сможет приобрести в результате полного израсходования в один прием его запасов горючего в безвоздушном и лишенном тяжести пространстве в том случае, когда ему пришлось бы преодолевать лишь инерцию его собственной массы при отсутствии каких-либо внешних препятствий вроде сопротивления воздуха или тормозящего действия поля тяготения. Для того чтобы корабль вселенной был пригоден для осуществления определенного путешествия в мировом пространстве, идеальный импульс силы его двигателей, в соответствии с только что сказанным, должен быть, по меньшой мере, равен сумме всех замедлений, сопротивлений и изменений скорости, которые кораблю предстоит испытать во время полета.
8. Дальность действия силы тяжести
Если бы формула Ньютона в точности выполнялась в мировом пространстве, то сила притяжения всякой массы нигде не становилась бы равной нулю, дальность действия этой силы была бы безгранична и нельзя было бы говорить о границе поля тяготения вокруг небесных тел.
Еще сравнительно недавно принято было думать, что даже самые далекие небесные светила связаны между собой тяготением. В настоящее время многие придерживаются того мнения, что притяжение Солнца не простирается даже до альфы Центавра, ближайшей к нам звезды*.
* Теоретически сила тяготения распространяется беспредельно и в этом не возникает никаких сомнений. Практически же взаимные притяжения звезд так малы, что не могут оказывать никакого влияния на их движения. (Прим. ред.)
Однако совершенно несомненно, что в пределах Солнечной системы формула Ньютона выполняется с такой точностью, что при всех расчетах межпланетных путешествий мы можем основываться на ней, как на чем-то совершенно достоверном. Здесь, следовательно, сферы притяжения отдельных тел действительно проникают одна в другую, благодаря чему и не существует областей пространства, неподверженных действию силы тяготения. Поэтому, если мы в последующем изложении и будем говорить о сферах притяжения Земли, Луны и т.п. то мы не будем подразумевать под этим термином точно ограниченного пространства, внутри которого действует поле притяжения Земли и замыкаемого снаружи как бы шарообразным мыльным пузырем; под сферой земного притяжения мы всюду будем понимать ту границу, за которой начинает преобладать сила притяжения какого-нибудь другого небесного тела. Сфера эта будет располагаться различно, смотря по тому, притяжение каких двух тел мы будем рассматривать, - неодинаково между Землей и Луной, Землей и Марсом, Землей н Солнцем.
9. Взаимно налагающиеся поля тяготения
Нам еще осталось пояснить взаимодействие различных полей тяготения и его последствия на примере. Лучше всего пригодны для этой цели два небесных тела, обладающие сравнимыми массами и отстоящие друг от друга на не черезмерно большом расстоянии; иначе было бы невозможно нанести их кривые тяготения на лист бумаги полностью, сохраняя правильный масштаб. Так, например, если бы мы пожелали воспользоваться для этой цели Землей и Луной, то лист бумаги, на котором нам пришлось бы строить чертеж, должен был бы обладать шириной по меньшей мере в 1 м, а высотой в 10 м. Поэтому мы вообразим себе пару небесных тел, диаметры которых относятся. как 1:2, а масса, (при равных плотностях) как 1 : 8. Пусть расстояние между этими телами равно 5 радиусам большего тела; тогда, в силу принятого отношения диаметров, это расстояние будет равно 10 радиусам тела меньшего. При таких данных мы получим весьма удобный и наглядный чертеж (рис.4). Из вышесказанного следует, что напряжения силы тяжести у поверхности (изображенные на чертеже отвесными линиями, составляющими продолжение радиусов звезд) относятся как 2:1, т.е. на поверхности большего тела всякая масса будет весить вдвое больше, чем на поверхности меньшего тела. Кроме того, мы убеждаемся в том, что площади, замыкаемые кривыми тяготения, относятся друг к другу, как 1:4, потому что помимо половинного напряжения силы тяжести меньшее тело обладает и половинным диаметром, а 1/2 х 1/2 = 1/4. Следовательно, с меньшего тела улететь вчетверо легче, чем с большего в том случае, если мы их будем рассматривать каждое в отдельности. В действительности же сделать это еще гораздо легче в силу того, что, как мы это сейчас пояснили, поля тяготения взаимодействуют и частично друг друга уничтожают.
Мы видим, что кривые тяготения взаимно пересекаются в точке Q. Опустив из этой точки перпендикуляр на горизонтальную линию, соединяющую центры обоих светил, мы получим точку S. Она будет являться так называемой «нейтральной точкой» или «точкой лишенной тяжести». То, что кривые пересекаются в точке Q, значит, что там перпендикуляры, опущенные на горизонтальную линию, будут равны, следовательно, силы притяжения будут одинаковы. А так как они, кроме того, направлены в противоположные стороны (в силу того, что всякая звезда притягивает к своему центру), то в этой точке обе равные, но противоположно направленные силы притяжения, уничтожаются, или, как говорят иначе, взаимно уравновешиваются. Какая-нибудь масса, например корабль вселенной, достигший этой точки, не будет более притягиваться ни в ту, ни в другую сторону.
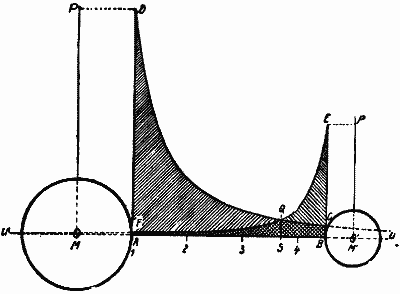
Здесь, если так можно выразиться, будет находиться граница действия силы тяжести или, короче говоря, граница тяжести. Поэтому точка S с точки зрения земного наблюдателя будет являться наивысшей точкой на пути от А до В, так как лишь до нее будет длиться подъем как от точки А, так и от точки В, а начиная от нее уже будет происходить спуск.
При этом лишенная тяжести точка разделит расстояние ММ' обоих небесных тел в отношении квадратных корней из их масс. Следовательно, в случае Земли и Луны, отношение масс которых равно 81 : 1, точка S находится в девять раз дальше от центра Земли, чем от центра Луны. При среднем расстояний от Земли до Луны в 384 400 км расстояние точки S от центра Земли составит 345 960 км, а от центра Луны 38 440 км.
Однако не следует думать, что силы тяготения обоих светил противодействуют одна другой только в этой именно точке. В действительности это противодействие имеет место па всем протяжении от одного светила до другого, но в других местах всюду преобладает притяжение одного из этих тел и притом именно того, кривая тяготения которого в этом месте выше. Чтобы найти, какое притяжение в действительности испытывает масса, находящаяся в каком-либо месте линии, соединяющей центры обоих светил (М и М'), нам всегда необходимо учитывать господствующие в этом месте силы притяжения обоих тел и затем вычитать из большей силы меньшую.
Такое положение вещей имело бы своим следствием тог факт, что человек, которого мы могли бы мысленно заставить подняться по веревочной лестнице с Земли на Луну, поднимаясь со ступеньки на ступеньку, постепенно терял бы свой вес. Добравшись до ступеньки, соответствующей точке, лишенной тяжести, он почувствовал бы себя совершенно невесомым. Продолжая свое восхождение, он смог бы заметить, что теперь он уже спускается на Луну, в силу чего ему пришлось бы перевернуться на лестиице и слезать по ней ногами вперед. При этом он вновь ощутил бы появление собственного веса, который стал бы постепенно возрастать по мере его слезания со ступеньки на ступеньку, пока наконец по достижении поверхности Луны вес его не стал бы равен 1/6 его веса на земной поверхности (рис. 5).
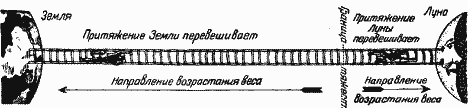
Рис. 5. Схема воображаемого подъема на веревочной лестнице с Земли на Луну.
Совершенно иным образом обстояло бы дело при свободном полете корабля вселенной от Земли до Луны. Так как он с точки зрения механики должен рассматриваться как лишенный точки опоры, то его вес не будет постепенно уменьшаться подобно весу человека в предыдущем примере, но будет равен нулю в течение всего того времени пока корабль будет осуществлять свободное падение вверх или вниз, иными словами, в течение всего того времени пока двигатели корабля не будут работать*. В силу этого пассажиры корабля вселенной не будут испытывать постепенного уменьшения своего веса по мере приближения точки, лишенной тяжести, но почувствуют себя совершенно невесомыми, начиная с момента прекращения действия двигателей и вплоть до того момента, в который двигатели вновь будут пущены в ход для торможения или для изменения направления полета (рис. 6).
* Или пока он не попадет в сопротивляющуюся среду, например в атмосферу планеты. (Прим. Ред.)

Рис. 6. Схема полета корабля вселенной о Земли на Луну.
Для того чтобы кораблю вселенной перелететь с большего небесного тела па меньшее, ему не нужно преодолевать полностью теоретического поля тяготения ADU (pиc.4). Чтобы достигнуть поверхности меньшего тела, ему придется бороться с притяжением большего тела не до конца пути, а только до точки S, за которой он сам начнет падать по направлению к цели. Следовательно, кораблю не придется полностью производить работы не только олицетворяемой площадью ADU, но также и той, которой соответствует площадь ABCD. Для такого nepeлета будет достаточно совершить работу, приходящуюся на долю площади FQD. Область ABCQF, являющаяся общей частью обоих площадей тяготения, отпадет так как в этом месте силы тяготения взаимно противодействуют. То же самое справедливо и для возвращения, в силу чего для этого излишне полностью производить работу BEU' или даже BEAF; необходимо только произвести работу CQE, которой на нашем чертеже соответствует область CQЕ, составляющая в данном частном случае только примерно половину площади BEU'. Мы установили таким образом, что работа, необходимая для перелета с одного небесного тела на другое, расположенное весьма близко от первого, не соответствует просто отношению из взаимодействующих сил напряжения (ADU : BEU'); в данном случае играют роль только ослабленные благодаря частичному взаимному уравновешиванию поля FQD и CQE.
В том случае, когда два рассматриваемые небесные тела значительно удалены друг от друга, их ослабленные поля становятся почти такими же, как поля неослабленные; это обусловливается тем обстоятельством, что тогда общая часть площадей тяготения (ABCQF) становится исчезающе малой по сравнению с остающимися площадями (FQD и CQE). В случае пары небесных тел Земля-Луна облегчение (ABCQF) составляют только 0,00363 общего напряжения поля земного тяготения и 0,07604 общей работы, необходимой для преодоления поля лунного тяготения.
Согласно К. Кранцу, вследствие этого начальная скорость в 11 087 м/сек, необходимая для полета с Земли на высоту Луны, уменьшается до 11 060 м/сек, а начальная скорость, необходимая для подъема с Луны, для обратного перелета на Землю, уменьшается с 2 400 до 2 360 м/сек.
10. Критическая точка. Граница Роша
Когда оба небесные тела находятся весьма близко друг от друга или когда одно из них весьма невелико по сравнению с другим, то мыслим случай, что точка, лишенная тяжести, весьма сильно приближается к меньшему телу или даже достигает поверхности последнего. Для обитателей маленького мирка это имело бы своим последствием то необычайное явление, что каждому из них, отважившемуся достичь «критической» точки, пришлось бы проделать невольный полет на небо, отделившись от поверхности родного светила и уносясь кажущимся образом вверх, а в действительности падая на большое тело*.
* Эти же силы, действуя в слабой степени на Землю со стороны Солнца и Луны, вызывают явление морских приливов, почему и называются приливообразующими или приливными. (Прим. ред.)
Возможно, что такие условия уже в настоящее время имеют место на ближайшем к Марсу спутнике Фобосе, а также и на пятом спутнике Юпитера. Если эти тела сейчас еще не распадаются на части, то они обязаны этим сцеплению частиц образующего их вещества, а не действию силы притяжения. Если бы наша Луна приблизилась к Земле примерно на два земных радиуса, то на обращенной к нам ее стороне должны были бы наблюдаться подобные же явления. Возможно (как это предполагается некоторыми исследователями), что Земля десятки тысяч лет тому назад обладала второй такой луной, значительно меньших размеров по сравнению с той, которую мы знаем в настоящее время. Распадение этой второй луны должно было начаться, когда заостренная, как у куриного яйца и вытянутая по направлению к Земле, часть ее придвинулась к нашей планете ближе точки, лишенной тяжести. Сначала слетело все, что свободно лежало на поверхности, после чего благодаря силе земного притяжения, приобретавшего все больший перевес, по тому же пути последовали так же и холмы и горы гибнущего спутника. Дальше не могло быть уже никакой остановки. Постепенно всесокрушающая сила земного притяжения как бы содрала кожу с разрушавшейся луны. После этого былой спутник Земли, раздробленный на миллиарды осколков, преобразовался в красивое двойное кольцо, висящее над земным экватором. Кольцо это в конце концов, все более и более сужаясь, рухнуло на Землю целой тучей осколков, двигавшихся по спиральным путям. Подобным же результатом разрушения спутника, по-видимому, является и современное кольцо Сатурна, которым мы любуемся в телескоп как одним из красивейших чудес неба.

В пользу такого взгляда говорит тот факт, что кольцо Сатурна полностью лежит внутри так называемой границы Роша, кладущей предел возможному существованию в этой зоне спутников.