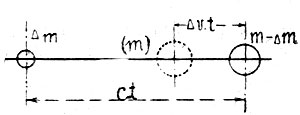
Фиг. 69
Предположим, что мы находимся вне влияния силы тяжести и помещаемся в
 Фиг. 69 |
Если в каждую секунду будет извергаться часть массы 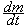 с постоянной скоростью с, то остающаяся масса получит ускорение
с постоянной скоростью с, то остающаяся масса получит ускорение
Пусть расход горючего так отрегулирован, что в любой момент секундное его потребление 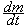 пропорционален остающейся массе m, так что
пропорционален остающейся массе m, так что
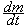 пропорционален остающейся массе m, так что
пропорционален остающейся массе m, так что
Тогда ускорение будет равномерным и независимым от массы
Расход массы следует закону
Поэтому
При начальных условиях t = 0 и m = m0, тогда
| ..........(2) |
Если на снаряд, обладающий собственным ускорением са действует сила тяжести с ускорением g противоположного знака, то полное ускорение будет
Пусть например, снаряд, находясь от центра земли в расстоянии r, движется, удаляясь от него, в радиальном направлении, и обозначим ускорение силы тяжести через g0 у поверхности земли, радиус которой r0 (фиг. 70). Тогда ускорение силы тяжести, направленное противоположно собственному ускорению снаряда на расстоянии r будет*
* Замечания о законе тяготения см. в конце III части.
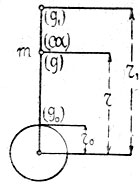 Фиг. 70. |
Далее
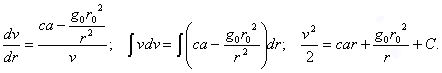
При начальных условиях (у поверхности земли) r = r0; v = 0, поэтому
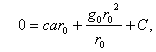
Поэтому
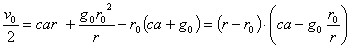 ..........(4)
..........(4)Если на расстоянии r1 и при достижении максимальной скорости v1 собственное ускорение снаряда исчезает, то он уподобляется телу, брошенному вертикально с начальной скоростью v1 и тогда в расстоянии
Из последних двух уравнений следует
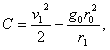
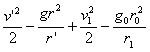 ..........(5)
..........(5)Если снаряд в расстоянии r1 от центра притяжения получил такую максимальную скорость v1 при которой, по исчезновении его собственного ускорения ca, и он под влиянием силы тяжести обратно не падает, то конечная скорость v' = 0 лишь при r' = ∞.
Тогда по уравнению (5)
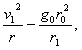 ..........(6)
..........(6)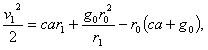
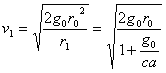 ..........(8)
..........(8)Время t1 по истечении которого будут достигнуты это расстояние r1 и эта наибольшая скорость, определяется из
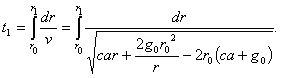
Так как нахождение этого интеграла представляет значительные трудности, то приходится отказаться от вычисления t1 при условии, что ускорение силы тяжести (g) изменяется в зависимости от расстояния, и принять некоторое значение gm между g0 и g1 и даже, для удобства вычисления, не среднее его значение
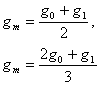
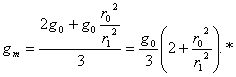
*При малом значении ас это среднее значение приемлемо. Точнее было бы выражение:
чтобы при ас = g0 полное ускорение β соответственно = 0.
Время полета получится, если вместо выражения полного ускорения
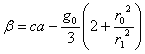 ..........(9)
..........(9)Тогда, в соответствии с уравнением (7) и (8),
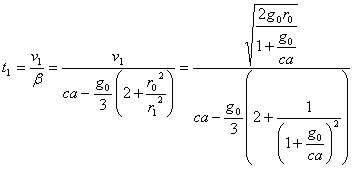 ..........(10)
..........(10)Подставляя это значение t1 в уравнение (2), получим
Разность m0 — m1 выражает вес горючего, которое за время t1 извергается с постоянной скоростью с для того, чтобы остающейся массе m1 сообщить наивысшую скорость v1 на расстоянии r1.
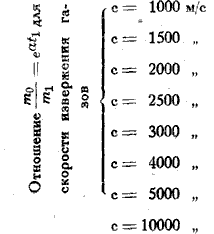
m1 представляет из себя полезный груз, освобожденный от влияния земного притяжения. Если мы определили скорость извержения газов с, собственное ускорение са и, исходя из практических соображений, то тогда по уравнениям (7, 8, 10 и 11) получим r1, v1, t1 и m0. В таблице I показано влияние различных значений с и са на отношение ![]() . При этом принято
. При этом принято
Из таблицы (стр. 198) видно, что влияние са сравнительно меньше, чем с. Поэтому следует сначала стремиться получить возможно большее значение с, а потом уже выбирать допустимое собственное ускорение снаряда. Последнее ощущается пассажирами, как увеличение тяжести, и поэтому ограничено физиологическими условиями. Чтобы определить его допустимое значение, заметим следующее: человек прыгающий с высоты h = 2 м, при соприкосновении с землей достигнет скорости 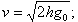 в момент касания с землей он сгибает колени и на пути около h1 = 0.5 м изменяет скорость до нуля. Поэтому замедление (β) можно определить по формуле
в момент касания с землей он сгибает колени и на пути около h1 = 0.5 м изменяет скорость до нуля. Поэтому замедление (β) можно определить по формуле
| Собственное ускорение са (м/с2) | 15 | 20 | 25 | 30 | 40 | 50 | 100 | 200 |
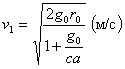 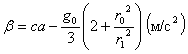 |
10600 8660 7.27 1192 |
9510 9680 12.00 762 |
8860 9150 16.76 565 |
8490 9470 21.61 448 |
7950 10000 32.35 319 |
7640 10200 41.18 248 |
7000 10650 90.76 117 |
6680 10890 190.46 57 |
 |
58 700 000 149 000 7570 1 270 388 87.3 35.7 6.0 |
4 160 000 25 000 2010 438 159 44.8 20.9 4.6 |
1 545 000 12 000 1160 282 110 34.1 16.7 4.1 |
675 000 7 750 825 216 88 28.7 14.6 3.8 |
346 000 4 950 587 164 70 24.2 12.8 3.6 |
240 000 3 840 495 143 62 22.2 11.9 3.5 |
120 300 2 400 347 108 49 18.7 10.4 3.2 |
39 130 2 000 299 95.5 44.7 17.2 9.8 3.1 |
Из обоих выражений имеем
Конечно, это замедление β человек испытывает лишь малую долю секунды, тогда как в нашем снаряде собственное ускорение са будет продолжаться минутами. Поэтому осторожнее принять са = от 20 до 30 м/с.2*
Труднее удовлетворить требование максимальной скорости извержения газов с. Наивысшая до сих пор достигнутая скорость при артиллерийской стрельбе равна около 1000 — 1500 м/с, но таковые скорости, как видно из таблицы I, дают слишком большие значения ![]() и потому не годятся. Поэтому следует принять, как наинизший предел, с = 2000 м/с, тогда, при са = 30 м/с2 получим отношение
и потому не годятся. Поэтому следует принять, как наинизший предел, с = 2000 м/с, тогда, при са = 30 м/с2 получим отношение ![]() =825.
=825.
При таковых низших значениях (са = 30; с = 2000) произведены последующие расчеты. Более благоприятные результаты при увеличенных значениях с даны в соответственных местах в виде сопоставления лишь результатов подсчета.
* Подробности о физиологическом действии ускорения см. ранее упомянутую работу Оберта.
При начале взлета (старта), секундная извергаемая масса определяется из уравнения (1с)
Поэтому
Следовательно, в начале взлета в секунду расходуется масса, составляющая значительную долю остающейся полезной.
Если мы устроим взрывы на подобие пушечных, то тогда придется брать большой мертвый вес, который соответственно увеличит начальную массу m0 снаряда. Чтобы избежать этого, расположим массу горючего m0 — m1 подобно тому, как это делается в ракете, чтобы сгорающие продукты извергались в безвоздушное пространство со скоростью с. Пусть секундный расход горючей массы соответствует своему сечению ракеты и наличному остатку ее массы; тогда можно принять, что каждое сечение пропорционально выше лежащей массе, и форма горючего будет похожа на башню с равным сопротивлением на сжатие (фиг. 71).
Масса, извергаемая в секунду через какое-нибудь сечение F определяется по уравнению (1с) и фиг. 71.
Далее
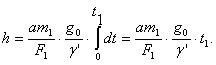
Обозначим через G1 = m1g0 отнесенный к поверхности земли вес остающейся массы снаряда; тогда
Пусть например, поднимаемый груз G1 = 2t (две тонны), а удельный вес горючего γ' = 1.5 т/м3, тогда для рассматриваемого случая
Принимая площадь верхнего сечения башни F1 = 0,332 м2, что соответствует кругу диаметром 0,65 м, получаем
| = 27м (фиг. 72). |
Сопротивление материала на сжатие будет при собственном ускорении са = 30 м/с2 (вместо обычного g = 9,8 м/с2)
Изыскание материала, который, при требуемой прочности, доставлял бы скорость извержения с и соответственную энергию, есть задача техники взрывчатых веществ.
До сих пор мы не принимали во внимание сопротивление воздуха.
Хотя вышеописанная форма снаряда (фиг. 72) выгодна для преодоления сопротивления воздуха, и хотя большие скорости имеют место лишь на значительной высоте, где атмосферы или совсем нет или она весьма разрежена, однако необходимо, хотя приблизительно, оценить влияние нижних плотных слоев воздуха.
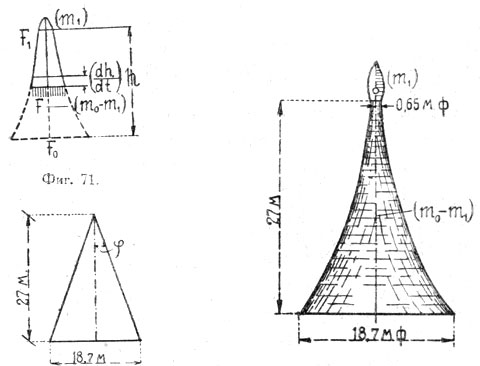 | |
| Фиг. 73. | |
По Лёсслю сопротивление W воздуха удельного веса γ движению тела миделевого сечения F, движущегося со скоростью v и перпендикулярно к F равно
Здесь g — ускорение силы тяжести, ψ — коэффициент, зависящий от формы тела (для плоскости движущейся в направлении по перпендикуляру к ней ψ = 1).
Происходящее, благодаря этому, замедление будет
Для рассматриваемого случая по уравнению (12)
Для конической формы башни (фиг. 73), имеем
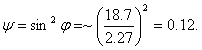
Поэтому
Для рассматриваемых пределов можно принять g=10 м/с. и по уравнению (4)
| r км | r-r0 км | 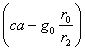 км/с | v2 км2/сек2 | γ по табл. III кг/м2 | кг/м2 |
6380 6381 6382 6383 6384 6385 6386 6388 6390 6395 6400 6410 6420 6430 6440 6460 6480 |
0 1 2 3 4 5 6 8 10 15 20 40 50 60 80 100 |
0.02020 0.02020 0.02020 0.02020 0.02020 0.02020 0.02020 0.02021 0.02021 0.02022 0.02023 0.02024 0.02026 0.02027 0.02028 0.02032 0.02035 |
0.00 0.04 0.08 0.122 0.162 0.202 0.243 0.323 0.404 0.606 0.810 1.214 1.620 2.028 2.434 3.250 4.070 |
1.30 1.15 1.00 0.90 0.80 0.70 0.62 0.48 0.375 0.215 0.105 0.0283 0.0074 0.00187 0.00045 0.000023 0.000001 |
0 4600 8000 11000 13000 14200 15100 15500 15200 13000 8500 3440 1200 370 110 7.5. 6.4. |
На высоте свыше 50 км над поверхностью земли при получающихся на них скоростях влияние сопротивления воздуха по уравнению (13) ничтожно. Примем более неблагоприятный случай, когда на высоте от 0 до 50 км среднее значение
Тогда среднее замедление по уравнению (13) будет
Для r=6430 км или r — r0 = 50 км из уравнения (4) имеем
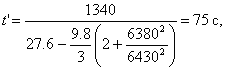
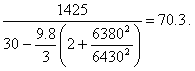
Итого разница во времени Δt = 4.7 с.
Далее, конечная скорость будет меньше на
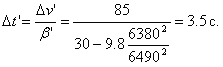
Продолжительность взрывов будет вместо данной в таблице t' = 448 с
| =et'1 = 933 вместо 825. |
Результат будет несколько лучше, если на протяжении первых 50 км мы просто увеличим собственное ускорение на Δβ = 2.4 м/с2. Тогда общая продолжительность извержения останется такой же, как и без сопротивления воздуха, т. е. 448 с, из которых первые 70.3 с будут соответствовать ас = 32.4 м/с2 при a= ![]() = 0.0162, а остальные 377.7 с — ас = 30 м/с2 при a = 0.015, и отношение будет
= 0.0162, а остальные 377.7 с — ас = 30 м/с2 при a = 0.015, и отношение будет
В нижеследующей таблице показано влияние сопротивления воздуха при других значениях ас и с на отношение
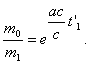
| с = 2000 м/с с = 2500 „ с = 3000 „ с = 4000 „ с = 5000 „ |
ас= 30 m/c2 t'1= 456 вместо 448с) | ас= 100 m/c2 t'1= 123 вместо 117с) | ас= 200 m/c2 t'1= 64 вместо 57с) |
| 933 вместо 825 235 „ 216 95 „ 88 30 „ 28 15 „ 14.6 |
468 вместо 347 138 „ 108 60 „ 49 22 „ 18.7 12 „ 10.4 |
602 вместо 299 166 „ 95.5 71 „ 44.7 25 „ 17.2 13 „ 9.8 |
Из таблицы видно, что с увеличением собственного ускорения aс влияние сопротивления воздуха весьма увеличивается; поэтому большая величина ас полученная за счет большой скорости, может оказатся менее выгодной, чем малая величина ас.
Мысли, изложенные выше, и выражающие идею движения тела благодаря длительным взрывам, преодолевающим силу тяжести, не новы. Они изложены уже в сочинении Жюль-Верна „Вокруг Луны", в котором он описывает способ уменьшения скорости ядра при помощи ракет. Также Курт Лассвиц, в своем романе „На двух планетах", описал применение извержения частиц со скоростью света, что дает весьма малое уменьшение веса снаряда.
О новых работах Годдара, Оберта и Валье было уже упомянуто в предисловии. Известный пионер воздухоплавания Германн Гансвинд указал на возможность устройства ракетного аэроплана еще в 1890 году; к тому же времени относятся работы и русского ученого Циолковского. Наконец, еще Ньютон в своих лекциях о принципе отдачи упомянул о возможности применить этот принцип для полета в безвоздушном пространстве.