Если снаряд падает с большого расстояния от центра притяжения (ср. предыдущую часть и фиг. 70) в пределах от r₁ до r₀ и скорость его должна от v₁ затормозиться до нуля, то на это потребуется то же время t₁, как и раньше (уравнение 10), и расход горючего , извергаемого уже в направлении движения. При подъеме и возвращении на землю время полета таким образом удвоится; отношение между начальной и конечной массами будет

При таком способе торможения и принятой скорости газов (с) отношение масс является весьма невыгодным. Поэтому следует изыскать иной способ спуска, например, при помощи тормозящего действия земной атмосферы.

По Лёсслю сопротивление воздуха летящему в нем телу равно

..........(14)

v — скорость тела в данный момент,

g — ускорение силы тяжести,

γ — удельный вес воздуха,

w — давление на единицу площади, перпендикулярной к направлению движения,

F — площадь поперечного сечения (тела), перпендикулярного к направлению движения,

ξ — коэффициент зависящий от формы тела (например, для плоской пластинки ξ равно 1, для выпуклого полушара ξ = 0.5).

Примем, что давление атмосферы, равное у поверхности земли р₀ и на высоте h — 0, изменяется по закону (фиг. 74).

Фиг. 74.

..........(15)

Тогда падение давления при изменении высоты на dy будет

Но с другой стороны

Так что

..........(16)

У поверхности земли y = h, и p=p₀. Поэтому

..........(17)

..........(16a)

Примем γ₀ = 1.293 кг/м³

р₀ = 0,76 м 13600 кг/м³ = 10330 кг/м² (вес ртутного столба).

Тогда

..........(17a)

По наблюдениям с баллон-зондами для высоты h — у = 10 км давление атмосферы равно около 210 ртутн. ст., поэтому

Это значение может быть получено и независимо от уравнению (15) при h от 100 до 1000 км. По наблюдениям за падением метеоритов, равно как на основании теоретических соображений, можно принять высоту атмосферы по меньшей мере равной h = 400 км (ср. напр. Trabert „Lehrbuch der kosmischen Physik " стр. 304). Это значение и принято в дальнейшем. Тогда из уравнения (17) и (17а) имеем

Для разных значений h — у вычислены соответствующие у и даны в таблице III (стр. 208).

Если тело приходит из мирового пространства на расстояние 400 км от земной поверхности или на расстояние r — 6780 км. от центра земли, и летит под влиянием земного тяготения, то, по уравнению (6), оно имеет скорость

Очевидно, что при радиальном падении эта скорость не может затормозиться до нуля без вреда как для самого снаряда, так и для его пассажиров. Однако, продолжительность торможения может быть значительно увеличена при тангенциальном входе тела в атмосферу.

Если тело подходит к земле из далекого расстояния и летит, подвергаясь лишь действию земного притяжения, то, если только оно падает на землю не радиально, оно описывает почти параболическую траекторию, фокусом которой служит центр земли.

Тогда для любого расстояния r скорость будет (см. фиг. 70)

При проходе непосредственно у земной поверхности касательная скорость будет

На границе же атмосферы касательная скорость будет

В пределах же атмосферы скорость будет около

h-y км	y км		h-y км	y км		h-y км	y км		h-y км	y км
0 1 2 3 4 5 10 15 20	400 399 398 397 396 395 390 385 380	1.3 1.15 1.00 0.90 0.80 0.70 0.375 0.205 0.105	25 30 35 40 45 50 55 60 65	375 370 365 360 355 350 345 340 335	0.055 0.0283 0.01464 0.0074 0.00376 0.00187 0.000915 0.000448 0.000217	70 75 80 85 90 95 100 105 110	330 325 320 315 310 305 300 295 290	0.000 102 5 0.000 049 7 0.000 023 0 0.000 010 6 0.000 004 9 0.000 002 2 0.000 000 98 0.000 000 423 0.000 000 185	150 200 400 - - - - - -	250 200 0 - - - - - -	0.000 000 000 13 0.000 000 000 000 002 3 0.000 000 000 000 000 000 - - - - - -

Этому сопротивлению по таблице IV соответствует высота от 750 до 100 км над поверхностью земли (фиг. 75).

Фиг. 75.

Вход снаряда в земную атмосферу будем предполагать таким, чтобы вершина параболического пути расположилась на высоте 75 км над поверхностью земли или на расстоянии

ТАБЛИЦА IV

h-y км	y км	r км	м/с2	кг/м3	кг/м2
400 200 150 110 105 100 95 90 85 80 75 70 65 60 55 50	0 200 250 290 295 300 305 310 315 320 325 330 335 340 345 350	6780 6580 6530 6490 6485 6480 6475 6470 6455 6460 6455 6450 6445 6440 6435 6430	8.69 9.21 9.36 9.48 9.50 9.51 9.53 9.54 9.56 9.57 9.59 9.60 9.62 9.63 9.65 9.66	0.000 000 000 000 000 000 0.000 000 000 000 002 3 0.000 000 000 13 0.000 000 185 0.000 000 423 0.000 000 98 0.000002 2 0.000 004 9 0.000 010 6 0.000 023 0 0.000 049 7 0.000 102 5 0.000 217 0.000 448 0.000 915 0.001 870	0.000 000 000 0.000 000 03 0.001 7 2.4 5.5 12.7 28.5 63.4 137 297 640 1320 2780 5720 11800 23900

Длина пути между высотами в 75 и 100 км, который является путем торможения, определяется по фиг. 75. Из уравнения параболы имеем

α' = 3°34'; 2α' = 7°8'.

Далее, с достаточным приближением, имеем

При этом, в биде первого приближения, принято, что путь не изменяется благодаря замедлению (влияние последнего особо рассмотрено в конце этой части).

На протяжении пути s_a замедление β массы m₁ снаряда благодаря сопротивлению воздуха w будет иметь переменное значение

Далее

Поэтому

При входе на путь торможения при у=у' имеем

В середине пути торможения для у — у_а имеем

Поэтому, при прохождении первой половины s_a пути торможения

..........(18)

Подставляем числовые значения

γ₀ = 1.3 кг/м³; Δr_a = r' — r_a = 100 — 75 = 25 км;

sa = 805 км;

h = 400 км = 400 000 м; g_a = 325 км; y' = 300 км.

Далее, как и раньше, g₀m₁ = вecy снаряда G₁, отнесенному к поверхности земли, = 2000 кг и F·ξ = 6,1 м² — площадь, соответствующая раскрытому парашюту, диаметром 2.8 м, расположенная перпендикулярно к направлению полета. Тогда наибольшее значение замедления на высоте 75 км будет

Подобным же образом вычислим скорость выхода снаряда из второй половины s_a пути торможения

Результатом уменьшения скорости будет изменение формы пути и снаряд вместо бывшей до сих пор параболы опишет эллипс, пройдя который снаряд опять пролетит по пути торможения, войдя на него уже со скоростью v₁ = 10.4 км/с. Благодаря короткому пути торможения дуга эллипса будет мало отличаться от параболы и поэтому длину нового пути торможения можно опять принять равной 2s_a = 2.805 = 1610 км.

По прохождении уже этого пути новая скорость выхода из него будет

Результатом этого нового уменьшения скорости получается вместо предыдущего, новый уменьшенный эллипс, по прохождении которого произойдет новое торможение в атмосфере со входной скоростью v₂ = 9.8 км/с. Примем опять длину тормозящего пути 2s_a = 1610 км — в действительности, он будет несколько длиннее и торможение будет сильнее. Тогда

Наконец, после еще одного подобного эллиптического пути и тормозного действия половины пути s_a скорость у вершины будет

Фиг. 76.

Для определения продолжительности прохождения снарядом разных эллипсов, достаточно показать таковое для одного из них (фиг. 76). Если тело массы m находится от центра земли Е в расстоянии r, то оно испытывает притяжение

Для поверхности земли при r — r₀, сила притяжения равна весу mg₀ тела

Если тело по фиг. 76 отстоит от центра притяжения на наименьшее (или наибольшее) расстояние r_а, то скорость будет v_a⊥r_a, и оно опишет эллипс с полуосями

Допуская небольшую ошибку, примем что скорости v₁, v₂ и т. д. выхода из путей торможения имеют место в вершине, где r_а = 6455 км; тогда, округляя, имеем

Продолжительность полета по каждому эллипсу вычисляется на основании закона площадей (уравнение 39 в конце III части)

Поэтому

..........(18a)

Следовательно, для прохождения всех пяти эллипсов (фиг. 77) потребуется следующее время

---

Всего t_а = 79 300 с = ~ 22,1 час.

Фиг. 77. Спуск ракеты Гоманна.

Начинающийся вслед за этим планирующий полет можно себе представить следующим образом: он начинается с высоты h — у_а = 75 км с тангенциальной скоростью v_a = 7.85 км/с, при которой центробежное ускорение равно ускорению силы тяжести g_a, так как v_a² = g_ar_a (см. стр. 212). Благодаря продолжающемуся замедлению β, под влиянием сопротивления воздуха, уменьшается скорость v и центробежное ускорение

..........(19)

Радиальное замедление можно получить благодаря действию сопротивления воздуха на несущую поверхность F₀, которая из первоначального горизонтального положения должна быть приведена в наклонное к нему при помощи руля высоты и наклон этот должен быть постепенно все больше и больше (см. фиг. 79)

..........(20)

Получающимся же одновременно касательным сопротивлением τ=ρ·tgα можно пренебречь по сравнению с большим замедлением β вдоль пути. Для того, чтобы управление высотой все время производилось легко, необходимо, чтобы лобовое сопротивление w не превышало того, которое было в начале планирования. Поэтому, из уравнений (14) и (16а)

..........(21)

Фиг. 78. Фиг. 79.

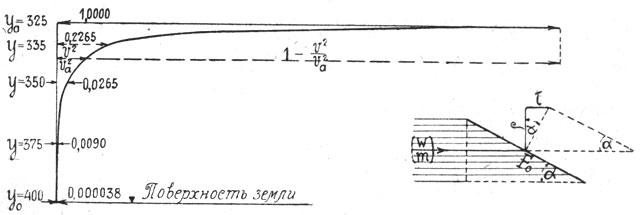
Иными словами каждой высоте должна соответствовать своя скорость полета. На фиг. 78 показано, как каждой высоте (у) соответствует отношение . Тот же чертеж дает и разность которая по уравнению 19 выражает приращение радиального ускорения (ρ) в масштабе 1:g. Далее, при достижении некоторой скорости v снаряд пройдет путь s при постоянном замедлении β — β_a

..........(22)

Этот наклон по уравнению (22) выражается так

..........(23)

На высоте h — у_а = 75 км или при y_а = 325 км при скорости

Полагая это замедление сохраняющимся до уклона получим высоту, до которой спустится снаряд по уравнению (23)

Пройденный путь будет (по уравнению 22)

Время полета

= ~ g

Поэтому

Учитывая, что в отношении β_a величина τ = ρ tg α не велика, угол α должен быть возможно меньше, по крайней мере max α = 20°, т. е.

Из предыдущего следует, что от высоты h — у = 75 до высоты 48 км над поверхностью земли, на протяжении s_b = 3250 км, при постоянной тормозной площади F=6,1 м² и постоянной несущей площади F₀ = 59 м² угол (α) наклона (встречи) несущей поверхности к горизонту должен увеличиваться от 0° до 20°, чтобы при неизменном сопротивлении воздуха w = 310 кг/м² скорость изменилась от v_а = 7850 до V_b = 1150 м/с, а радиальное замедление (ρ) росло от 0 до полной величины ускорения силы тяжести (см. фиг. 80 от А до Б).

Начиная с высоты h — у_b = 48 км, во избежание быстрого падения, необходимо уменьшить замедление движения, и для того, чтобы уже не пользоваться парашютообразной тормозящей поверхностью F, следует применить для торможения несущую поверхность F₀, которая дает составляющую τ = 3.56 м/с² = 0.00356 км/с², которая и будет далее тормозить движение. Однако и это значение τ следует применять не до конца, так как иначе, после короткого полета может быть крутой спуск — падение; поэтому, при постоянном ρ (= ускорению силы тяжести), замедление в полете следует делать все меньшим, например, при переходе из положения В далее за D (фиг. 80), перемещая несущую поверхность F₀ в горизонтальное положение.

Для каждой точки траектории имеем соотношение

..........(24)

Предположим, что планирование у земли происходит под углом 45°; тогда для y = y₀= 400 км

Фиг. 80. Фиг. 81.

В конце пути (на фиг. 80, F), касательная составляющая τ сопротивления воздуха на крыло равна 0. При этом замедление β_min происходит лишь благодаря форме самого снаряда (фиг. 81) и равно

Подставляем числовые величины

d=1,5 (наименьший допустимый диаметр снаряда);

В конце оставшегося пути скорость полета определится из

Для простоты расчета примем, что β изменяется от 3,56 до 0,102 м/с² не непрерывно, а скачками на четырех участках В — С, С — D, D — Е, и Е — F (фиг. 80), именно, имея значение β_c — 3.5 м/с², β_d = 1.0 м/с², β_е = 0.2 м/с² и β_f = 0.102 м/с², а наклоны путей примем

Тогда для конца каждого участка имеем:

Для участка В — С по уравнению (24)

Далее, из уравнения (21)

Для участка C — D

Для участка D — E

Для участка E — F

Длина всего планирующего полета будет

Полная продолжительность спуска, считая от первого взлета в атмосферу до приземления равна около

При определении эллипсов торможения предполагалось, что в точке касания у подхода параболы к первому эллипсу, остальные эллипсы начинаются сразу, без постепенного перехода из одного в другой. В действительности действие торможения происходит не сразу, а постепенно, по длине каждого эллипса, и путь снаряда будет не эллиптический, а спиральный. Вдоль пути его снаряд будет встречать более низкие и потому более плотные, слои воздуха, что повлечет за собою и большее его сопротивление и, соответственно, большее замедление против принятого раньше. В результате желательно оценить вид эллипса выхода, равно как и наклон и укорочение его оси.

Для определения картины возможного изменения обстоятельств полета, в дальнейшем первый после параболы эллипс (фиг. 77) заменен спиралью.

Для этого на фиг. 75 угол 4α' = 14°16', внутри которого парабола рассекает слои воздуха, разделен на 6 частей по Δφ =2°22⅔ каждая, внутри которых длина соответствующего отрезка спирали равна около . В случае нужды слева от угла (фиг. 77) будем предполагать еще и дальнейшие такие же углы. Примем, что в точках соприкосновения соседних путей Δs происходит действие торможения в виде ударов, соответствующих мгновенному уменьшению скорости где v обозначает конечную скорость на предыдущем участке, а β вычисляется при помощи таблицы IV по формуле

Если в таблице нет непосредственного значения w, то оно получается прямолинейным интерполированием, что дает результат в запас (несколько больше истинных). Для начальной точки каждой ветви эллипса величины r₁, v₁ и α₁ считаются данными и получаются через Δv, как результаты исследования предыдущего эллипса.

Далее применяем уравнения

(см. уравнения 45 и 46 в связи с законом площадей) и (см. уравнение эллипса).

Из них получается угол φ₁ между лучем входа и главной осью рассматриваемого элиппса ; далеее, так как Δφ= 2°22⅔, получаем и угол φ₂ = φ₁ ±Δφ между конечным лучем и главной осью а, и, наконец, соответствующие значения для конечной точки ветви эллипса

(см. уравнение эллипса), (см. уравнение 41) и (см. закон площадей и уравнение 39) и т. д., пока не будет достигнуто расстояние r> 6480

Произведенные вычисления здесь приводятся.

Для сравнения ниже сопоставлены элементы пути торможения для эллиптического спирального путей.

Полученный эллипс выхода с а = 12 486 вместо 25 000 км и b = √119 500 000 = 10 931 вместо 16 800 км значительно меньше вычисленного первого эллипса торможения; их обе большие оси отклоняются друг от друга на угол 7°41' — 7°8' = 33'. Ближайшая точка выхода от земли будет в расстоянии

Можно заключить, что в действительности вместо ранее упомянутых пяти эллипсов можно ограничиться двумя эллипсами торможения и перейти потом прямо на круговую траэкторию, в особенности, если тормозная площадь F будет несколько увеличена.

В заключение следует определить, нельзя ли при выходе снаряда в тормозящую воздушную оболочку сразу перейти на круговую траекторию не совершая полетов по эллипсам. Это, конечно, осуществимо лишь при помощи руля высоты. Его применение не встречает препятствий, так как и без этого он необходим для дальнейшего планирующего полета.

Для первого, наиболее неблагоприятного в смысле влияния торможения, подсчета допустим, что снаряд достигает вершины параболы при r_а = 6455 км с замедленной, благодаря сопротивлению воздуха, скоростью около . Если снаряд при этих условиях должен далее описывать круговую траекторию, то необходимо, чтобы имело место центростремительное ускорение

Следовательно, необходимо добавочное радиальное ускорение

Фиг. 82.

При уменьшении скорости полета v постепенно будет требоваться все меньше и радиальное ускорение ρ, которое можно уменьшать соответственным уменьшением угла α. Для v_a = 10,75 км/с и r_а = 6455 км и при той же площади F₀=59 м², несущей поверхности, которая необходима при планировании, имеем:

Масса снаряда

Далее, при круговой траектории

Угол α будет постепенно уменьшаться и достигнет 0° при переходе к свободной круговой скорости 7.85 км/с. Наибольшее значение замедления на высоте 75 км при v_max=11.1 км/с и при парашюте, площадью F=6.1 м² было ранее получено равным

Во время принудительного кругового движения на той же высоте 75 км, замедление при мгновенной скорости v будет

У вершины параболы для s = 0

Поэтому в конце принудительного и в начале свободного полета по кругу, т. е. при v = 7,85 км/с, снаряд пройдет от вершины параболы путь

На прохождение этого пути потребуется время, определяемое из

Для t=0, т. е. для вершины параболы

Поэтому

Таким образом с момента прохождения вершины параболы до конца планирования пройдет время

Спуск на землю без полета по эллипсам торможения поэтому является вполне возможным. Несколько иначе обстоит дело во время вынужденного кругового полета, когда пассажиры внутри снаряда будут прижиматься к верхней части снаряда благодаря действию центробежной силы и будут лететь головой или спиной вниз, что может быть затруднит маневрирование. Пилот должен наблюдать, чтобы ему не попасть преждевременно в более плотные слои атмосферы, что (фиг. 78) может повести к падению. Если же он полетит выше, чем следует, то ему придется в худшем случае вылететь из земной атмосферы и описать больший или меньший эллипс и во время такого пути на свободе выбрать наиболее удобный спуск.

В кажущемся противоречии с вышеописанным способом спуска находится явление воспламенения болидов и метеоритов, из чего как бы можно заключить, что проникающее из мирового пространства в земную атмосферу тело должно, благодаря сопротивлению воздуха, подвергнуться сильному нагреванию. Но против этого можно возразить, что эти метеориты обладают значительно большей скоростью, нежели наш снаряд. Последний, как мы предполагали, подвергается только действию земного притяжения и обладает, как и земля, тем же движением, которое она имеет вокруг солнца со скоростью 30 км/с. Между тем метеориты получают на расстоянии от солнца, равным радиусу земной орбиты, благодаря притяжению солнца, скорость по отношению к последнему около 42 км/с. Поэтому, если они летят навстречу земли, то при скорости последней около 30 км/с они будут иметь скорость относительно нее 42 + 30 = 72 км/с вместо 11.1 км/с, каковой обладает наш снаряд. Так как сопротивление воздуха пропорционально квадрату скорости, то при падении метеорита в наиболее неблагоприятном направлении оно будет в = 43 раза больше, чем при полете снаряда.

Однако, не следует забывать, что при уменьшении скорости от

Принимая, как и раньше, массу

получим

Эта энергия должна перейти или в вихревое движение воздуха или в теплоту или в оба вместе. При бывших до сих пор рассуждениях о спуске на землю молчаливо допускалось первое, т. е. переход энергии в движение воздуха. Другой крайний случай — переход ее всецело в теплоту дает следующее:

Принимая механический эквивалент тепла получим выделяющее при спуске число калорий

(единицы тепла = Wärmeeinheiten).

При предыдущем предположении возможно быстрейшего торможения применяемый парашют будет сильно нагрет и сгорит. Поэтому необходимо проходить тормозной участок (фиг. 80) применяя несколько раз последовательно серию парашютов соответственной формы, пока, наконец, не перейдем на планирование в точке В, где скорость равна уже лишь 1150 м/с и в дальнейшем нечего опасаться нагревания.

Для уменьшения же опасности воспламенения, торможение должно быть принято с таким расчетом, чтобы нагретые поверхности имели достаточное время передать теплоту наружу через излучение. В общем, возникающая при торможении от скорости v' до скорости v энергия равна

Это соответствует секундному приходу тепла

Если допускаемый секундный приход тепла известен, то замедление при торможении для момента, когда скорость равна v, должны быть не более

Допускаемый секундный приход тепла должен уравновешиваться возможным его расходом через проводимость и излучение. Предполагая поверхность снаряда ребристой, можно принять этот секундный приток = , что при дает

Вычислим замедление для разных v

Для получения столь малых замедлений почти не требуется парашюта, так как для незначительного торможения достаточно сопротивления воздуха движению тела и крыльев снаряда.

Полный путь s при спуске получается из

При этом на долю вынужденного кругового движения при v = 11 100 до 7850 м/с приходится = 249 450 000 м = около 6 облетов кругом земли
при 7850 до 4000 м/с. = 139 920 000 м = около 3.5 облетов

и для v = 4000 до 0 м/с = 21 330 000 м = около 0.5 облета.

Все это произошло бы, если предположить, что вся энергия торможения переходит в тепло.

Действительность находится между обеими границами. Во всяком случае при спуске на землю необходимо учитывать следующее:

1. Так как тормозить приходится не сильно, то можно выбирать парашют сравнительно небольшой.

2. Парашют должен производить воздушные вихри как можно лучше, для чего ему следует придать соответствующую форму (условия 1 и 2 будут наилучше выполнены, если, по предложению Валье, парашют будет состоять из ряда конусов, расположенных вдоль общей оси на большом расстоянии друг от друга и с вершинами, направленными вперед).

3. В предупреждение возможности воспламенения следует взять с собою побольше запасных парашютов (конусов).

4. Снаряд должен быть снабжен не только крыльями, но и металлическими ребрами для охлаждения.

Работу последних в условиях громадных скоростей и разреженной атмосферы необходимо еще исследовать.