 Фиг. 9. Р. Годдар. |
Американский профессор Годдар в 1912—1913 гг. дал теорию полета ракеты и составил уравнения ее движения, которые он опубликовал в своей статье „A Method of Reaching Extreme Altitudes“ (Washington, 1919).
Он ставит задачу в следующем виде: „Какова должна быть минимальная начальная масса ракеты, чтобы в результате можно было поднять один фунт груза на желаемую высоту. При этом предполагается непрерывный расход массы, например, в виде горючего“.
Вначале он выводит точные формулы и указывает, что применения их приводят к неразрешимой задаче вариационного исчисления, затем дает приближенный, достаточный для практики, метод расчета.
Роберт Годдар опубликовал свои исследования о полете ракет в 1919 году. Им, повидимому, впервые были произведены научные опыты по определению коэффициента полезного действия ракет и по исследованию вопроса о наилучшем их устройстве.
Ниже мы помещаем краткую биографию Годдара (сообщенную нам им самим), содержание его книги „Способ достижения больших высот“ и описание взятых им патентов на новые типы ракет.
 Фиг. 9. Р. Годдар. |
Роберт Годдар (фиг. 9) родился в Ворчестере (С. А. С. Ш.) 5 октября 1882 года. Родителями его были Наум (Nahum) Данфорд Годдар и Фанни-Луиза (Hoyt) Годдар. Звание баккалавра (В. Sc.) он получил в Ворчестерском Политехническом институте в 1908 году, а ученые степени — в Университете Кларка: в 1910 году (А. М.) и в 1911 году (Ph. D.) — доктора физики. В 1908—1909 гг. он состоял преподавателем физики в Ворчестерском Политехническом институте, в 1912—1913 гг. инструктором по физическим исследованиям в Принцтонском университете, в 1914 — 1915 гг. — инструктором и почетным членом Физического о-ва в Университете Кларка, в 1915—1919 гг. — помощником профессора физики там же, и с 1919 года профессором физики там же. С 1923 года — директором физических лабораторий там же. Во время мировой войны в 1918 г., служил в качестве директора по исследованиям при С. А. Сигнальном корпусе, в Ворчестерском Политехническом Институте и при Обсерватории на горе Вильсон. Член A. A. A. S., член Американского Физического о-ва, член Американского Метеорологического о-ва, Американского Института Социальных Знаний, О-ва Sigmaxi, Sigma, Alpha, Epsilon. Женат на Эсфири-Христине Киск с июня 1924 года.
С 1929 года Годдар перешел на службу в Американское Военное Министерство, куда он был зачислен полковником (Signal Corps of the U. S. Army). Существенная поддержка в его опытах была оказана из Авиофонда Д. Гугенгейма.
Главнейшие научные работы его: электропроводимость порохов, кристаллические выпрямители, механические силы диэлектриков в магнитном поле, цвета интерференции в облаках, устойчивость самолетов, образование газов при электрических разрядах в пустотных трубках и метод достижения больших высот для научных исследований.
На фиг. 10 полезная масса весом 1 фунт обозначена H. Эту массу и должна поднять ракета на требуемую высоту по вертикальному направлению. Взрывчатый материал В заключен в оболочку К. Материя В при взрыве извергается вниз с постоянной скоростью с. В дальнейшем предполагается, что оболочка К постепенно отваливается, по мере сгорания горючего, так что низ ракеты остается все время плоским.
 Фиг. 10. Теоретическая ракета Годдара. |
Введем следующие обозначения :
М — начальная масса ракеты.
m — масса извергнутая во время t
v — скорость полета ракеты во время t
R — сила сопротивления воздуха в абсолютных единицах.
g — ускорение силы тяжести.
dm — масса, извергнутая во время dt.
k — постоянная часть массы dm, соответствующая оболочке К, отпадающей от ракеты со скоростью О относительно к оставшейся части ракеты.
dv — приращение скорости, получаемое остающейся частью ракеты.
Дифференциальное уравнение движения ракеты получим на основании третьего закона Ньютона, исходя из условий, что момент количества движения в момент t равен таковому же в момент t +dt + импульс сил сопротивления воздуха и тяжести
Сопротивление R можно принять независимым от длины ракеты, если пренебречь „поверхностным трением“. Это допустимо для скоростей, которые больше скоростей звука, если только поперечное сечение будет наибольшим у головы аппарата.
Величины R, g и v выражаются проще в функции высоты s, если только и S выразится так же, и тогда уравнение (1) примет вид
Что такой minimum массы существует, раз данная масса на данной высоте имеет наперед заданную скорость, вытекает из следующих соображений: если на какой нибудь промежуточной высоте скорость подъема чрезмерно велика, то сопротивление воздуха, зависящее от квадрата скорости, также будет очень велико. С другой стороны, если скорость подъема будет очень мала, то потребная отдача должна преодолевать притяжение земли слишком долго. В обоих случаях необходимая масса горючего получается чрезмерно большей. Очевидно, что скорость подъема должна иметь значение, соответствующее каждому месту по высоте. Иными словами, необходимо неизвестную функцию v=f(s) определить так, чтобы m было minimum.
Можно было бы подставить в уравнении (3) вместо v и dv их значения f(s) и ![]() и получить величину (m) при помощи интегрирования. Однако, при условии, что m должно быть minimum, вариация (σ m) должна быть равна нулю и тогда определится f(s). Это определение приводит к новой и неразрешимой задаче вариационного исчисления.*
и получить величину (m) при помощи интегрирования. Однако, при условии, что m должно быть minimum, вариация (σ m) должна быть равна нулю и тогда определится f(s). Это определение приводит к новой и неразрешимой задаче вариационного исчисления.*
* Позднее эта задача была разрешена в Германии Гамелем, перевод статьи которого мы ниже помещаем.
Для получения возможного и в то же время применимого на практике метода решения задачи, Годдар предлагает приближенный метод решения ее, который состоит в следующем.
Разделим высоту на большое число частей (n) и примем, что R, g и ускорение подъема будут постоянными на каждом участке.
Пусть для каждой части (интервала) — v выражается: v = at, где (а) — постоянная ускорения.
Тогда, вместо уравнения движения (3), мы получим линейное уравнение первого порядка относительно m и t
Умножая и деля правую часть его на (a + g) получим решение

Тогда имеем
 ........ (5)
........ (5)Это уравнение имеет место для каждого интервала по высоте, для которого R, g и а — постоянны.
Можно ввести дальнейшее упрощение, исходя из условия, что начальная масса должна быть такова, чтобы в результате конечная поднятая масса равнялась 1 фунту.
При таких условиях начальная масса ракеты в начале первого интервала или так называемая полная начальная масса ее, требуемая для поднятия ее на все (n) интервалов, будет результатом сложения n количеств, полученных таким путем.
Полагая конечную массу равной единице, мы получим М — m = 1 и, подставляя это выражение в уравнение (5), получим массу в начале рассматриваемого интервала
 ........ (6)
........ (6)Если R и g равны нулю, то
 ........ (7)
........ (7)Из уравнений (6) и (7) видно громадное значение качества ракеты, которое зависит от величины с — скорости извержения газов. Эта величина входит в степень е в виде знаменателя степени и потому выгодно как можно больше увеличивать с, уменьшая в то же время k. Например, предположим, что мы уменьшили с (1 — k) в 10 раз, тогда  увеличится в 10 степени раз, другими словами, масса на каждом интервале будет против прежней массы больше в 10 раз умноженной сама на себя. По опытам Годдара, скорость истечения газов в усовершенствованной ракете может быть доведена до величины в 6 — 7 раз большей (2434 м/с) по сравнению со скоростью газов, например, в корабельной ракете (314м/с) и потому масса первой может быть сделана в
увеличится в 10 степени раз, другими словами, масса на каждом интервале будет против прежней массы больше в 10 раз умноженной сама на себя. По опытам Годдара, скорость истечения газов в усовершенствованной ракете может быть доведена до величины в 6 — 7 раз большей (2434 м/с) по сравнению со скоростью газов, например, в корабельной ракете (314м/с) и потому масса первой может быть сделана в ![]() массы второй.
массы второй.
Необходимо, чтобы масса горючего была возможно больше по отношению к остальной массе ракеты. Хотя при опытах Годдара со стальными ракетами стенки последних делались весьма толстыми, соответствующими наружной штриховке на фиг. 10, однако, эти стенки могли бы быть толсты до толщины сплошных наружных линий (k) того же чертежа. Годдар полагает, что минимум массы оболочки в его опытах мог бы быть доведен до 120 граммов на 1 грамм пороха.
Обратимся снова к уравнениям (6) и (7) и напомним, что в них
М = минимальная масса ракеты в каждом интервале высоты подъема.
R — сопротивление воздуха в фунтах, отнесенное на поперечное сечение S ракеты на высоте полета. Если через Р мы обозначим сопротивление воздуха на единицу площади этого сечения, то ![]() где ρ — плотность воздуха на высоте полета, a ρ0 — на уровне моря.
где ρ — плотность воздуха на высоте полета, a ρ0 — на уровне моря.
а — ускорение в (в фут/сек2), принимаемое постоянным на соответствующем интервале.
g — ускорение силы тяжести.
t — время полета на всем интервале.
с (1— k) — эффективная скорость истечения газов. Так можно назвать скорость истечения, потому, что задача останется неизменной, если предположить ракету, состоящую исключительно из горючего, вырывающегося со скоростью с (1— k). Напомним, что через (с) обозначена действительная скорость вырывающихся газов, а через (k) часть всей массы ракеты, состоящей из материала иного, чем горючее. Эффективная скорость предполагается постоянной на взятом интервале.
Высота подъема разделена на интервалы достаточно короткие, чтобы на них вышеупомянутые величины могли быть приняты постоянными. Уравнения (6) и (7) позволяют найти minimum массы М для каждого интервала при средних значениях R и g на этом интервале. Полная начальная масса, необходимая для подъема конечной массы в 1 фунт на желаемую высоту найдется как результат умножения этих частных масс М.
На основании своих опытов, Годдар принимает с = 7500 ф/с. Далее k = 1/15; с (1-k) = 7000 ф/с.
Для вычисления сопротивления воздуха Годдар делит высоту подъема на 7 интервалов (фиг. 10) и коэффициент Р определяет по формуле
 ........ (8)
........ (8)В таблице I показаны данные для разных выбранных интервалов (фиг. 11). Выше 120 000 футов плотность вычислена по эмпирическому правилу, считая, что она уменьшается вдвое при подъеме на каждые 3.5 мили. Для проверки было сделано сравнение результатов, полученных этим способом, с теми, которые дает Wegener на основании вероятных давлений на этих высотах, именно: средняя плотность между двумя уровнями получается умножением разности давлений на них (по Wegener'y) на 13.6 и разделением на разницу уровней в см. Первым способом получаются плотности от 3 до 10 раз больше, чем по Вегенеру, что служит в запас. Плотностями на высотах выше 700 000 фут. пренебрегаем.
ТАБЛИЦА I
| Интервалы | Длина интервалов | Возвышение верхнего конца интервала над уровнем моря | Средняя плотность по отношению к ρ0 | Среднее ускорение силы тяжести по отношению к таковому же у уровня моря | ||
| Футы | Метры | Футы | Метры | |||
| S1 S2 S3 S4 S5 S6 S7 S8 | 5 000 10 000 10 000 20 000 40 000 40 000 75 000 300 000 3 415 000 |
1 524 3 048 3 048 6 096 12 192 12 192 22 860 91 440 1 040 900 |
5 000 15 000 25 000 45 000 85 000 125 000 200 000 500 000 3 915 000 |
1 524 4 572 7 620 13 716 25 908 38 100 60 960 152 400 1 193 300 |
0.928 0.730 0.520 0.278 0.080 0.015 0.0026 0.000025 .... .... |
1 1 1 1 1 1 1 1 0.839 0.684 |

В таблице II и III приведены данные подсчетов, произведенных: для таблицы II от уровня моря и для таблицы III от высоты s3 = 15 000 фут. = 4572 м. Метод подсчета для обеих таблиц одинаков и состоит в следующем: в начале каждого интервала мы имеем скорость полета, уже приобретенную ракетой в конце предыдущих, например v0, которая конечно, равна нулю в начале 1-го интервала. Обозначим конечную скорость на интервале v1 тогда
Величина t определяется из уравнения
 ........ (10)
........ (10)Подсчет ![]() не требует пояснений. Величина R получается по данной Р, по средней ординате между v0 и v1 (формула 8). умноженной на S и
не требует пояснений. Величина R получается по данной Р, по средней ординате между v0 и v1 (формула 8). умноженной на S и ![]() (фиг. 11).
(фиг. 11).
Величина начальной массы М на интервале, необходимой для поднятия на конец интервала конечной массы в 1 фунт получается из уравнения 7. Наконец, определяется отношение величин масс по уравнениям 6 и 7, т. е.

Это есть отношение необходимой начальной массы, при учете влияния R и g, к необходимой массе для поднятия 1 фунта на ту же высоту без учета R и g. Весь подсчет должен быть повторен до тех пор пока это отношение не получится минимальным, что и даст minimum массы М. В таблицах II и III такие минимумы обозначены звездочками. Подсчеты производятся для каждого интервала начиная с 1-го.
Следует заметить, что хотя Р и плотность воздуха не являются постоянными для каждого интервала, однако полученные результаты в предположении средних значений этих величин не далеки от истинных, так как Р возрастает, а плотность убывает с высотой.
| Интервалы | V1 фут/сек |
at | t сек |
a |  |
 |
 |
М фн |
 |
 |
М2 фнт |
 |
МR1 фнт |
 |
МR2 фнт |
Время движения и интервал | ||||
| S1 * |
500 800 1 000 1 200 1 500 2 000 |
500 800 1 000 1 200 1 500 |
20.0 12.5 10.0 8.34 6.7 5.0 |
25 64 100 144 226 400 |
0.0716 0.1145 0.143 0.172 0.215 0.287 |
0.1630 0.1720 0.1890 0.212 0.2475 0.309 |
1.074 1.120 1.185 1.153 1.242 1.332 |
1.176 1.186 1.207 1.235 1.276 1.362 |
7.36 20.0 31.25 61.4 104.6 202.5 |
6.85 18.5 29.0 57.0 98.0 188.0 |
0.120 0.193 0.219 0.323 0.378 0.436 |
1.1972 1.2218 1.252 1.311 1.380 1.5195 |
1.113 1.092 1.086 1.106 1.112 1.138 |
1.458 |
1.5584 | 3.94 | 4.586 | 167.3 | 203.91 | 10.0 |
| S2
* |
1 100 1 200 1 400 |
100 200 400 |
9.54 9.10 8.33 |
10.47 22.0 47.9 |
0.0143 0.0286 0.0574 |
0.0578 0.0704 0.0954 |
1.014 1.034 1.060 |
1.061 1.073 1.100 |
153.3 166.6 216.0 |
112.1 121.6 158.7 |
2.64 2.24 1.97 |
1.222 1.237 1.297 |
1.206 1.199 1.223 |
1.150 |
1.4860 | 1.665 | 3.155 | 6.73 | 20.60 | 19.1 |
| S3
* |
1 300 1 400 1 600 |
100 200 400 |
8.0 7.7 7.15 |
12.5 25.8 56.4 |
0.0143 0.0286 0.0574 |
0.0508 0.0637 0.0906 |
1.014 1.034 1.060 |
1.052 1.066 1.096 |
250.0 262.8 294.5 |
130.0 136.9 152.6 |
2.925 2.37 1.74 |
1.204 1.222 1.261 |
1.186 1.182 1.191 |
1.137 |
1.462 | 1.589 | 2.974 | 5.62 | 16.52 | 26.8 |
| S4
* |
1 500 1 600 1 700 1 800 |
100 200 300 400 |
13.8 13.33 12.90 12.5 |
7.23 15.0 23.24 33.25 |
0.0143 0.0286 0.0429 0.0574 |
0.0775 0.0898 0.1022 0.1170 |
1.014 1.034 1.046 1.060 |
1.080 1.094 1.107 1.123 |
339.0 372.0 394.0 424.0 |
94.3 101.5 109.4 118.0 |
2.42 2.17 1.975 1.81 |
1.273 1.297 1.319 1.346 |
1.255 1.253 1.26 1.267 |
1.198 |
1.626 | 1.92 | 3.91 | 11.33 | 33.73 | 40.13 |
| S5
* |
1 700 1 800 2 000 |
100 200 400 |
24.25 23.7 22.24 |
4.125 8.45 18.0 |
0.0143 0.0286 0.0574 |
0.1258 0.1366 0.159 |
1.014 1.034 1.060 |
1.133 1.146 1.173 |
439.0 480.0 535.0 |
35.1 38.4 42.8 |
0.974 0.951 1.245 |
1.262 1.2845 1.242 |
1.186 1.321 1.246 |
1.313 |
1.711 | 2.694 | 4.304 | 40.70 | 88.45 | 63.83 |
| S6
* |
1 900 2 000 2 200 |
100 200 400 |
21.7 21.1 20.0 |
4.62 9.50 20.0 |
0.0143 0.0286 0.0574 |
0.1135 0.1255 0.1490 |
1.014 1.034 1.060 |
1.12 1.133 1.16 |
567.0 603.0 669.0 |
8.50 9.01 10.02 |
0.232 0.2175 0.1923 |
1.1478 1.162 1.1907 |
1.13 1.123 1.124 |
1.280 |
1.3406 | 2.488 | 2.810 | 29.76 | 36.02 | 84.93 |
S7 |
5 160 3 393 |
3 160 1 393 |
21.0 27.8 |
150 50 |
0.4523 0.199 |
0.5452 0.3276 |
1.572 1.218 |
1.725 1.387 |
1878.0 1122.0 |
4.84 3.1 |
0.0264 0.0355 |
1.7442 1.4007 |
1.108 1.15 |
2.97 1.900 |
3.022 1.9319 |
52.6 10.79 |
53.96 11.13 |
2.63 X 106 7.03 X 103 |
2.70 X 106 7.28 X 103 |
105.93 112.73 |
S8 |
10 719 683 |
5 630 2 840 |
37.5 55.8 |
150 50 |
0.804 0.399 |
0.976 0.652 |
2.23 1.49 |
2.65 1.92 |
10600 4000. |
0.272 0.0994 |
0.00146 0.00121 |
2.6524 1.9211 |
1.19 1.293 |
7.02 3.680 |
7.0288 3.6932 |
1192.0 117.4 |
1193.7 117.54 |
2.88 X 1011 4.67 X 107 |
2.88 X 1011 4.67 X 107 |
143.43 168.53 |
S9 |
30 533 |
23 000 |
153.5 472.5 |
150 50 |
3.29 3.38 |
3.89 4.85 |
26.9 29.13 |
48.8 129.0 |
- - |
- - |
1.19 1.293 |
- - |
48.8 129.0 |
- - |
2380.0 16700.0 |
1.995 X 1015 |
1.995 X 1015 |
1.25 X 1057 |
1.25 X 1057 |
296.93 641.03 |
| Интервалы | v1 фут/сек |
at | t сек |
a |  |
 |
 |
М фн |
 |
 |
М2 фнт |
 |
МR1 фнт |
||||
| S3 * |
500 800 1 000 1 500 |
500 800 1 000 1 500 |
40 25 20 13.4 |
12.5 32.0 50.0 112.0 |
0.0715 0.1147 0.142 0.2145 |
0.255 0.2277 0.235 0.277 |
1.074 1.120 1.152 1.24 |
1.29 1.256 1.263 1.318 |
11.53 30.70 46.7 165.0 |
5.97 16.0 24.3 83.3 |
0.134 0.250 0.295 0.570 |
1.329 1.300 1.341 1.499 |
1.236 1.162 1.165 1.207 |
1.574 |
1.718 | 5.225 | 6.545 |
| S4
* |
900 1 000 1 300 1 800 |
100 200 500 1 000 |
23.7 22.2 19.1 15.4 |
4.23 9.00 26.2 65.0 |
0.0143 0.0286 0.0714 0.1430 |
0.1227 0.1305 0.1645 0.2136 |
1.013 1.034 1.073 1.152 |
1.132 1.137 1.177 1.238 |
95.7 108.8 165.0 305.0 |
27.7 31.4 46.25 87.9 |
0.764 0.767 0.794 0.908 |
1.232 1.242 1.318 1.455 |
1.216 1.200 1.227 1.263 |
1.293 |
1.518 | 2.581 | 3.794 |
| S5
* |
1 100 1 200 1 300 1 400 1 500 2 200 |
100 200 300 400 500 1 000 |
38.1 36.5 34.75 33.3 32.1 26.1 |
2.625 5.74 8.4 12.0 15.6 21.4 |
0.0124 0.0286 0.0430 0.0571 0.0715 0.1147 |
0.1888 0.1960 0.202 0.210 0.2192 0.268 |
1.013 1.03 1.044 1.058 1.073 1.12 |
1.207 1.215 1.223 1.233 1.245 1.308 |
150.1 170.0 195.0 218.0 243.5 417.0 |
12.0 13.55 15.65 17.49 19.45 33.4 |
0.347 0.362 0.384 0.397 0.520 0.623 |
1.278 1.293 1.306 1.325 1.372 1.501 |
1.261 1.255 1.250 1.252 1.280 1.340 |
1.495 |
1.685 | 4.32 | 5.594 |
| S6
* |
1600 1800 1900 2000 2100 2200 |
300 500 600 700 800 900 |
27.7 25.07 25.0 24.2 23.6 22.8 |
10.8 19.5 24.0 28.9 33.8 40.00 |
0.0430 0.0714 0.0857 0.1002 0.1142 0.1285 |
0.1690 0.1890 0.201 0.212 0.224 0.237 |
1.045 1.074 1.091 1.105 1.118 1.124 |
1.184 1.206 1.223 1.234 1.249 1.266 |
343.0 406.0 430.0 460.0 510.0 534.0 |
5.16 6.10 6.43 6.90 7.65 8.02 |
0.1203 0.1186 0.1150 0.1134 0.1165 0.1115 |
1.206 1.230 1.248 1.260 1.278 1.295 |
1.153 1.147 1.142 1.140 1.142 1.151 |
1.522 |
1.581 | 4.66 | 5.075 |
Следует сначала пояснить, почему для интервалов s7 и s8 не подсчитан minimum M. Хотя для предыдущих интервалов эти minimum'ы определились легко, попытка определить их для s7 и s8 показала, что они имеют место лишь для весьма больших скоростей v1; для s7 второстепенный minimum имеет место уже при v = 8000 ф/с. Minimum для этого интервала не был получен даже для v1=30000 ф/с., хотя потребное для этой скорости ускорение равнялось уже 6000 ф/с2. Это объясняется тем, что для интервала s7 отношение ![]() весьма мало и что (а) входит в знаменатель величины, определяющей R по уравнению (6), так что влияние большого ускорения парализует увеличение сопротивления R.
весьма мало и что (а) входит в знаменатель величины, определяющей R по уравнению (6), так что влияние большого ускорения парализует увеличение сопротивления R.
Поэтому для того, чтобы начальная масса для интервала s7 была minimum, ускорение должно быть весьма большим, что повлечет опасные напряжения в ракете и в инструментах, которые могут в ней находиться, не говоря уже о трудностях зажигания и взрывания при подобном ускорении. Поэтому осторожнее принять для интервалов s7 и s8 ускорение умеренной величины и не назначать для них скоростей v1 как это делалось для предыдущих интервалов. При подсчетах были приняты два ускорения: 50 ф/с2 (15 м/с2) и 150 ф/с2 (45,7м/с2). Подсчеты для интервала s9 объяснены ниже.
Было бы интересно определить, как может снизиться эффективная скорость с (1 — k) по сравнению с 7000 ф/с, чтобы полет ракеты оставался еще практически осуществимым. Для этого подсчитаны и приведены в таблицах добавочные столбцы.
В первом добавочном столбце при подсчете М2 была принята эффективная скорость в с (1 — k) = 3500 ф/с, каковой могут соответствовать разные комбинации с и k, например: 1) с = 3750 ф/с и k =![]() , 2) с = 7500 ф/с и k = 0.533. Последняя комбинация показывает, что большая часть ракеты состоит из оболочки и механизмов и меньшая из горючего.
, 2) с = 7500 ф/с и k = 0.533. Последняя комбинация показывает, что большая часть ракеты состоит из оболочки и механизмов и меньшая из горючего.
Следующий столбец MR1 составлен в предположении устройства, при котором оболочка постепенно отпадает k = ![]() , а скорость истечения газов — такая же, как и у корабельной ракеты (1029.25 ф/с). В этом случае эффективная скорость будет
, а скорость истечения газов — такая же, как и у корабельной ракеты (1029.25 ф/с). В этом случае эффективная скорость будет
с (1 — k) = 1029.25 ( 1 — ![]() ) = 960 ф/с.
) = 960 ф/с.
Третий столбец MR2 составлен в предположении, что ракета составлена из пучков корабельных ракет (Cast on ship), (фиг. 12), расположенных один над другим. Взрывание начинается с нижнего пучка, который затем отпадает, потом взрывается и отпадает следующий и т. д.
Для ракет этого типа отношение массы пороха к остальной массе ракеты равно ¼. Поэтому ее эффективная скорость
Поперечное сечение на каждом интервале принято в 1 кв. дюйм за исключением интервала s9. Это возможно допустить, так как наибольшие массы, вычисленные для интервалов s1 — s8 немного отличаются от 1 фунта.
Полная начальная масса, необходимая для подъема одного фунта от уровня моря до верхних границ интервалов s6, s7 и s8 даны в таблице IV. Они получены умножением друг на друга минимумов масс (обозначенных звездочками в таблице II), начиная от s1 до рассматриваемого интервала включительно.
Наибольшая высота подъема, которой достигнет масса в один фунт, однако, не будет равна высоте верхнего конца рассматриваемого интервала, но будет значительно превышать ее, так как один фунт достигнет этого конца с значительной скоростью и будет подниматься выше после того, как сгорит все горючее, пока скорость не обратится в нуль под влиянием притяжения земли и сопротивления воздуха. Эта добавочная высота может быть определена следующим образом.
Обозначим:
vn — скорость одного фунта при окончании взрывов (у конца интервала).
h — добавочную высоту подъема.
р — среднее сопротивление воздуха (в фунтах — poundals).
(Поперечное сечение принято = 1 дм2). Тогда имеем

Например, для s6 — p = 1.59
„ s7 — p = 0.28 (а = 50)
выше s7 — p = 0.465 (а = 150)
для s8 — p — ничтожно мало.
Высоты, полученные с учетом h, названы в таблице IV „наибольшими достигаемыми высотами“.
Очевидно, что если старт будет производиться не от уровня моря, а с большой высоты, то и достигаемая высота подъема будет значительно больше, так как плотность воздуха значительно уменьшается.
| Интервалы | Высота верхнего конца | Наибольшая достигаемая высота | Время достижения наибольшей высоты от уровня моря | Полная начальная масса (фунты) для подъема 1 фунта конечной массы | |||||||||||
| Ускорения (а) | Старт от уровня моря | Старт с 15 000 футов | |||||||||||||
| фут/с | м/с | футы | километры | футы | клм | = 7000 ф/с |
= 3500 ф/с = 1067 м/с |
= 960 ф/с = 293 м/с |
= 257.3 ф/с = 78 м/с |
= 257.3 ф/с = 78 м/с |
|||||
| S6 | - | - | 38 | 56 | 144.13 | 3.665 | 12.61 | 2030.0 | 2.66 | 6.95 | 702.0 | ||||
| S7 | 50 150 | 15.2 45.7 | 200 000 200 000 | 61 61 | 377 500 610 000 | 115 186 | 217.73 265.93 | 5.14 6.40 | 24.36 38.10 | 2.26 X 104 | 2.00 X 1015 | 2.28 X 1014 | 3.74 4.65 | 13.38 20.90 | 7820.0 37 800.0 |
| S8 | 50 150 | 15.2 45.7 | 500 000 500 000 | 152 152 | 2 310 000 | 374 704 | 380.53 475.23 | 9.875 12.33 | 89.60 267.70 | 2.66 X 106 1.318 X 108 | 2.55 X 1019 5.77 X 1026 | 2.89 X 1018 6.53 X 1025 | 7.19 8.97 | 49.30 147.30 | 4.51 X 107 |
| S9 | 50 150 | 15.2 45.7 | 3 915 000 | 2838 1193 | ∞ ∞ | ∞ ∞ | ∞ ∞ | 1274.0 602.0 | 6.37 X 105 | 5.32 X 1021 2.49 X 1020 | 3.21 X 1076 3.32 X 1071 | 3.63 X 1075 3.76 X 1070 | 926.0 438.0 | 8.22 X 105 3.51 X 105 | 1.82 X 1021 |
| ф/с= | Малая обыкнов. | Корабельная Costons ship | Большая сталь- ная Годдара | Водород + кислород старта 4572 м | ф/с= | Малая обыкнов. | Корабельная Costons ship | Большая сталь- ная Годдара | Водород + кислород старта 4572 м | ||
Вес заряда в кг b/a | 0.120 0.223 1/5 1/0,8 | 0.640 0.130 1/5 1/0,8 | 19.1 0.082 1/2300 1 | 54 53.546 1/1,08 1/119 | 19.7 19.246 1/1,02 1/43,5 | С м/с С (1 — k) м/с Высота подъема | 292 58 метр - | 1029 78.4 149 402 | - - 0.05 - | 2865 - ∞ - | 3627 - ∞ - |
В таблице III даны минимальные массы М, подсчитанные для старта, соответствующего интервалу s3 (15 000 фут) при начальной скорости нуль и эффективной скорости 7000 ф/с., как и в таблице II. Случайно имеет совпадение, что скорость v1 для минимума М на интервале s6 таблицы III равна скорости v1 для того же интервала по таблице II. В этом случае применяются те же подсчеты, как и для s7, и разница между обоими случаями будет лишь в том, что масса, необходимая для достижения интервала s7 будет больше при старте от уровня моря.
Расчеты, начиная с высоты 15 000 футов, произведены для пониженных эффективных скоростей (таблица IV), так как старт с большой высоты является выгодным только при таких скоростях.
Из таблицы IV видно, что для подъема на высоту 437 миль (2 310 000 фут. = 700 км) при эффективной скорости с (1-k) = 7000 ф/с (2134 м/с) необходима минимальная масса 12.33 фунта для подъема 1 фунта от уровня моря. При с (1-k = 3500 ф/с. (1570 м/с), эта масса все же будет невелика, например, при высоте 230 миль (370 км) от уровня моря, каковую можно считать уже пределом атмосферы, необходимо 90 фунтов; при высоте 118 миль (190 км) — где сфера геокорония — 38 фунтов. При старте с высоты 15 000 футов (4570 м) эти массы будут соответственно 49.3 и 20.9 фунтов.
Большая разница в величине полных начальных масс для ракет с большим и малым качеством объясняется степенным характером уравнений (6) и (7). Если эффективная скорость уменьшается в два раза (с 7000 до 3500 ф/с), то минимальные массы даже в случае неучета сопротивления воздуха увеличиваются пропорционально квадрату, а при учете сопротивления воздуха и в большей степени. Подобным же образом при эффективной скорости 960 ф/с (293 м/с), которую имеет облегченная ракета при одинаковой скорости извержения газов с корабельной ракетой (Cast on ship rocket), минимальная масса по сравнению с той, которая получается при с (1-k = 7000 ф/с (2133м/с) увеличится в 7.28* степени. Для группы же корабельных ракет (фиг. 3) величина минимальной массы возрастет в 27.2-ой** степени.
![]()
Такие большие массы указывают на невозможность пользоваться малыми скоростями истечения газов. Например для случая MR2 (табл. II и IV), когда мы имеем группу корабельных ракет (фиг. 12) для подъема 1 фунта на высоту 232 миль (190 км), полная начальная масса должна равняться 2.89 X 1018 фунтов, т. е. быть в шесть раз больше массы всего земного шара. Вообще значения масс MR1 и MR2 показывают непригодность этих случаев для практики.
В предыдущих рассуждениях конечная масса ракеты принималась в 1 фунт. Если таковой вес имеют инструменты, то полная конечная масса должна быть 3 — 4 фунта. При определении веса полной начальной массы следует иметь в виду, что она возрастает несколько слабее, чем возрастает конечная масса, когда последняя делается больше 1 фунта (см. ранее выведенные уравнения).
Выше было указано на большое влияние сопротивления воздуха, которое пропорционально площади поперечного сечения ракеты. При вычислении minimum'a массы М для каждого интервала, эта площадь принималась равной 1 дм2. Если мы соорудим аппарат длинным, узким и возможно компактным, то можно допустить площадь поперечного сечения и в один кв. дюйм при весе аппарата в 1 фунт. Из таблиц II и III видно, что при эффективных скоростях в 7000 и 3500 ф/с, начальные массы во всех интервалах (исключая s9) превосходят 1 фунт лишь немного. В двух случаях, относящихся к „Cast on ship "— ракете, начальные массы значительно больше. Поэтому, если площадь поперечного сечения будет больше 1 дм2, то начальные массы значительно возрастут. Вследствие этого важно стремиться к тому, чтобы эта площадь была даже меньше 1 дм2. Причиной служит то, что при определении полной начальной массы, когда мы умножали друг на друга частные минимальные массы, мы в том же отношении помножали и площади поперечных сечений. Иными словами, мы как бы имели много ракет, каждая площадью в 1 дм2, поставленных рядом и образующих пучёк. Но в этом случае площадь поперечного сечения пучка будет пропорциональна его массе, а не 2/3 степени от массы, как это имело бы место, если бы ракета при увеличении, сохраняла подобную форму, что и принималось в расчет при определении минимальных начальных масс.
Поэтому „полная начальная масса“ будет в действительности вычислена, при условии, что ее единичные площади поперечного сечения больше 1 дм2 на 1 фнт., за исключением конечного интервала, в котором сохраняется нагрузка в 1 фунт на 1 дм2, и достичь 1 дм2 в предыдущих интервалах можно лишь при повторных подсчетах.
Приведем здесь простой пример того, что и простой подсчет вместо применения уравнений 6 и 7 указывает на вероятность величин полных начальных масс ракет, приведенных в таблице IV. Рассмотрим для простоты, ракету, форма которой дана на фиг. 10 и предположим, что сначала взрывается 1/3 ее массы, со скоростью 7000 ф/с, затем 1/3 оставшейся массы и т. д. Тогда, по формуле равенства моментов, оставшаяся масса каждый раз получит добавочную скорость 3500 ф/с. При таких условиях, после четвертого взрыва останется масса 16/81начальной (около 1/5) и скорость ее будет 14 000 ф/с (4267 м/с). Эта скорость достаточна для поднятия ракеты на высоту 580 миль (933 км), (по формуле v2 = 2 gh), если пренебречь сопротивлением воздуха; при учете же последнего высота будет меньше.
Рассмотренный простой пример на практике неосуществим, так как в действительности поднимается при каждом взрыве гораздо большая масса по сравнению со всей массой, чем предположено в примере, и кроме того не предвиден вес камеры. Однако, результат будет тот же, если мы будем производить взрывы малых зарядов в быстрой последовательности, что мы теперь и рассмотрим на примере.
Пусть ракета весит 10 фунтов и имеет 2 фунта горючего и одновременно взрывается 1/8 фунта, а в секунду 8 раз со скоростью газов 6000 ф/с,, т. е. гораздо меньшей, чем при опытах даже в пустоте.
Предположим далее, для простоты, что ракета поднимается прямо вверх и каждый взрыв происходит мгновенно; скорость же остается между двумя соседними взрывами постоянной.
После первого взрыва 1/8 фунта масса в 97/8 фунта поднимется вверх с некоторой скоростью v0. Эту скорость можно найти из уравнения моментов количества движения. Но она будет немного меньше благодаря земному притяжению и в конце 1/8 сек. будет равна
V01 = v0 — gt За это время ракета пройдет путь
В начале второго промежутка в 1/8 сек., оставшаяся масса получит добавочную скорость в 76.8 ф/с и можно аналогичным способом определить конечную скорость и путь.
Расчеты дают следующие результаты:
Для времени до 1/2 секунды: | v01 = 291.1 ф/с; s = 91.98 ф. v01 = 603.8 ф/с; s = 335.48 ф. v01 = 1284.1 ф/с; s = 1315.68 ф. |
Эти числа хорошо согласуются с теми, которые были даны для s1 в таблице II. В приведенном подсчете сопротивление воздуха не играло большой роли до v 1000 ф/с.
Результаты предыдущих подсчетов, приведенные в таблице IV показывают, что при помощи ракеты можно достичь большой высоты — 2 310 000 фут. (700 км) при умеренной массе ракеты, лишь бы скорость истечения газов была велика. Поэтому не безъинтересно рассмотреть вопрос, нельзя ли получить таким же образом „параболическую“, соответствующую земле, скорость для аппарата не чрезмерно большой начальной массы.
Теоретически рассуждая, получаем, что масса, брошенная с поверхности земли со скоростью 6.95 миль/с (11 190 м/с), (без учета сопротивления воздуха), поднимается на бесконечно большую высоту в бесконечно большое время, т. е. никогда не вернется. Конечно такое метание тела без учета сопротивления воздуха невозможно. Кроме того на тело будут оказывать влияние другие небесные тела.
Однако, рассмотрим следующий допустимый случай.
Если ракета, о которой говорилось ранее, достигнет верхнего конца интервала s8 с ускорением 50 или 150 ф/с2, и это ускорение сохранится на достаточном расстоянии дальше s8, до тех пор, пока не будет достигнута параболическая скорость, то ее оставшаяся масса более никогда не вернется.
Обозначим через s9 интервал, у верхнего края которого скорость становится параболической. Этот интервал будет иметь разные величины в зависимости от принятых ускорений, так как параболическая скорость уменьшается с возрастанием расстояния от центра земли.
Обозначим через
u — параболическую скорость на высоте Н над поверхностью земли.
v1 — скорость ракеты у верхнего конца интервала s8.
s0 — высоту верхнего конца s8 над уровнем моря.
20 900 000 фут. (6371 км) — радиус земли.
Тогда имеем
Зависимость параболической скорости от расстояния аппарата от центра земли выражается формулой
 ........ (13)
........ (13)Даже если мы предположим, что плотность воздуха уменьшается в 2 раза на каждые 3.5 мили (5.64 км), то и тогда уменьшение скорости будет весьма мало от верхнего края s8 (500 000 фут = 152 400 м) до 1 000 000 фут (= 304 000 м).
Действительно, обозначим уменьшение скорости, благодаря сопротивлению воздуха, через W. Тогда имеем
Из этой формулы получаем, что потеря скорости меньше 10 ф/с, для а = 150 ф/с2) даже если предположить, что ![]() постоянно на всем интервале и равно значению его для 500 000 ф. (т. е. 2.73·10-9). Полные начальные массы, необходимые для подъема на бесконечную высоту, при двух принятых ускорениях, даны в таблице IV/ Из таблицы видно, что они изумительно малы, если только с (1—k) велико. Например, при эффективной скорости 7000 ф/с и ускорении 150 ф/с2, полная начальная масса при старте от уровня моря, равна 602 фунтам, а при старте с 15 000 фут (4572 м) — 438 фунт.
постоянно на всем интервале и равно значению его для 500 000 ф. (т. е. 2.73·10-9). Полные начальные массы, необходимые для подъема на бесконечную высоту, при двух принятых ускорениях, даны в таблице IV/ Из таблицы видно, что они изумительно малы, если только с (1—k) велико. Например, при эффективной скорости 7000 ф/с и ускорении 150 ф/с2, полная начальная масса при старте от уровня моря, равна 602 фунтам, а при старте с 15 000 фут (4572 м) — 438 фунт.
Масса сильно увеличится при уменьшении эффективной скорости. Например, если с (1—k) = ![]() = 3500 ф/с, то полная начальная масса при старте с высоты 15 000 фут будет 350 000 фунт. Эта масса немного уменьшится при ускорении большем 150 ф/с2.
= 3500 ф/с, то полная начальная масса при старте с высоты 15 000 фут будет 350 000 фунт. Эта масса немного уменьшится при ускорении большем 150 ф/с2.
Если в качестве горючего взять смесь кислорода с водородом, то при скоростях извержения соответственно равных 9400 и 11 900 ф/с и при старте с 15 000 фут. получим полные начальные массы соответственно 119 и 43.5 фунтов.
Для сравнения с данными пороховых ракет, вычисленными на основании формул приближенного метода и приведенных в таблице IV, в примечании к той же таблице сопоставлены данные Годдара о других ракетах: обыкновенной малой, „Cast-on-ship "— ракете, большой стальной, примененной им для опытов и для ракеты, где горючее не порох, а смесь водорода с кислородом.
Для того, чтобы по уменьшении количества горючего во время полета ракеты, ей не приходилось нести с собой бесполезную часть оболочки, в которой находилось уже использованное горючее, Годдар предложил делать ракету составной, ненужные части которой постепенно отпадали бы от ракеты по мере сгорания горючего. На фиг. 12 уже был приведен грубый пример подобной составной ракеты, образованной из пучков обыкновенных корабельных ракет (Cast-on-ship-rocket).
Годдар дает примеры и более совершенных типов — пороховых ракет в случае если полная начальная масса ракеты должна быть, по условиям высокого полета, большой.
 | ||
| Фиг. 12. | Фиг. 13. Составные ракеты Годдара. | Фиг. 14. |
Он предвидит две возможности: 1) Каждая из составляющих ракет делается малой, и они взрываются поштучно или группами, так что в каждый промежуток времени общая масса уменьшается лишь на малую величину (фиг. 13) и 2) Каждая из составляющих ракет делается возможно большей, так что вес сбрасываемой каждый раз пустой оболочки составляет значительную часть полного веса ракеты (фиг. 14). Не говоря уже о более легкой постройке, применять составную ракету второго типа является более предпочтительным. Но они должны быть длинными и узкими, иначе сопротивление воздуха почти пустой каждой части будет больше, чем у равной по весу группы частей ракеты первого веса, коих сочетание является более компактным. Следует еще заметить, что в случае большого числа очень малых частей составной ракеты, вес их оболочек и устройств будет составлять значительную часть полного веса, в то время как и площадь поверхностей оболочек, заключающих горючее, также будет максимум.
Простой подсчет показывает возможность и преимущество применения малого числа сравнительно больших ракет (или групп их), исходя из условия, что чем больше каждая отдельная ракета, тем меньше отношение веса металла ее к весу горючего.
Такое исчисление может быть произведено при нахождении числа составляющих ракет для второго случая (фиг. 14), которое требуется при той же полной начальной массе и при прочих условиях таких же, как и в первом случае (фиг. 13) при постепенном убывании массы с нулевою относительною скоростью.
При первом случае (фиг. 13) можно применить уравнение (7), пренебрегая R и g, так как, посколько мы обращаем внимание на (1 — k), выражение не будет зависеть от того, включены ли в него R и g или нет, найдем условия, которые должны иметь место для второго случая (фиг. 14), чтобы полная начальная масса была одинакова с ракетой по фиг. 13.
Предположим, что оболочка сбрасывается последовательно в конце каждого из (n) равных промежутков времени; скорость извержения газов — с, как и раньше. Полная начальная масса получается как произведение начальных масс для каждого интервала, по уравнению (7), при k = 0, предполагая конечную массу для каждого интервала, как и прежде, в 1 фунт; после первого умножения начальные массы множатся еще на числа, большие единицы, в которых превышение над единицей соответствует весу (А) оболочек, которые отпадают в конце интервалов.
Обращаясь к случаю первому (фиг. 13), разделим время на такие же п равных промежутков. Тогда, при условии равенства начальных масс в обоих случаях, мы будем иметь
 ........ (15)
........ (15)Тогда число составляющих ракет (или групп их) для обоих случаев, (по уравнению 16) соответственно 5 и 9, при условии, что n — целое число.
 Фиг. 15. Схемы ракет Годдара. |
Эти числа могут быть и меньше, хотя при этом необходимо увеличить полные начальные массы.
Американский профессор Годдар в 1915-18 гг. произвел ряд опытов с ракетами разных типов по определению их качества или отдачи. Последней называется отношение кинетической энергии вырывающихся из ракеты газов к тепловой энергии горючего. Опыты производились как под атмосферным давлением, так и в пустоте с порохом разных сортов. Кроме того определялись скорости истечения газов.
Виды испытанных ракет. На фиг. 15 изображены схемы ракет:
a) — обыкновенная, полного веса 120 граммов, в том числе заряд пороха 23 гр.;
b) — большая корабельная ракета (Cast on ship) весом 640, включая заряд пороха 130 гр.;
c) — малая стальная ракета, которая испытывалась в трех видах: с короткой дюзой (9 см.), средней дюзой (14.2 см.) и длинной дюзой (19.2 см.) *.
d) — большая стальная ракета.
* Годдар в своем сочинении не указывает точные длины дюз, но дает их фотографии вместе с масштабом, при помощи которого мы приблизительно определили длины дюз.
В ракетах (с) и (d) раструб дюзы имел конусообразную форму с углом при вершине 8°. Заряд пороха помещался за дюзой и длина его С могла изменяться при помощи вкладыша.
Результаты опытов приведены в таблице V, из которой видно, что наихудшее качество в обыкновенной ракете; оно немного выше в корабельной ракете и значительно повышается в стальных ракетах (до 64.53%).
| Ракета | Горючее | Качество | Скорость истечения газов | Примечание | |
| футы/с | м/с | ||||
| а) Опыты в атмосфере | |||||
| Обыкновенная ракета „Cast on ship“ ракета Малая стальная ракета - - - |
порох порох порох „Du Pont“ порох „Infaillible“ порох „Infaillible“ порох „Du Pont“ | 1.86% 2.21 44.73 41.88 44.78 57.25 64.53 | 957.6 1029.25 6257 6832 7064 7987 7515 | 292 314 1907 2082 2154 2434 2290 | 1) Качеством называется отношение кинетической энергии вырывающихся из ракеты газов к тепловой энергии горючего. 2) В пустоте скорости несколько больше при одинаковой длине заряда и массе пороха, чем в атмосфере. Порох „Du Pont“ дает в пустоте большую скорость при длинах дюзы: средней и короткой. При больших дюзах разницы нет. 3) Порох „Infaillible“ дает в пустоте скорости больше — до 22%. 4) Дюзы средней длины дают скорости больше, чем короткие и длинные. 5) Есть основание полагать, что в действительности, в пустоте скорости значительно больше, полученных в таблице, благодаря несовершенству опытов. |
| b) Опыты в пустоте | |||||
| Малая стальная ракета - - |
порох „Du Pont“ порох „Infaillible“ - | 39.73 52.93 55.90 |
5897 7680 7893 |
1797 2340 2405 | |
| с) Скорости при горючем: смесь водорода с кислородом | |||||
| Водород + кислород (жидкий или твердый) |
5500 — 7500 | ||||
Три причины влияют на улучшение качества ракеты: 1) термодинамические свойства горючего и устройство соответствующей формы и длины конической дюзы, через которую вырываются газы так, чтобы вся их энергия расширения превращалась в кинетическую и чтобы происходило полное сгорание; 2) возможное облегчение веса ракеты с применением максимума веса горючего, помещаемого в наименьшем объеме, минимума веса оболочки и остального груза; 3) применение составных ракет, оболочки которых последовательно отпадают, по мере сгорания заключавшегося в них горючего.
Годдар, говоря в своем сочинении „Метод достижения больших высот“ о возможности поднимать регистрирующие инструменты в высокие слои атмосферы при помощи ракеты, указывает на возможность применения парашюта для безопасного и замедленного спуска их на землю.
Хотя скорости падения на большой высоте и могут быть большими, например около 3500 м/с., однако, сопротивление воздуха движению парашюта может быть и не чрезмерным, благодаря малой плотности воздуха. Все же следует иметь в виду, что парашют значительно задержит быстроту и увеличит время спуска приборов и отыскать их будет не легко.
Следовало бы изобрести парашют, который в начале падения допускал бы большую скорость и замедлял бы ее лишь при подходе к земле.
Влияние парашюта в области малой плотности воздуха иллюстрируется следующим примером:
Пусть аппарат весит 1 фунт (0.45 кг), имеет парашют площадью в 1 кв. фут (0.0929 м2), спускается с высоты 1228 000 фут. (свыше 200 миль = 350 км) и не испытывает никакого атмосферного сопротивления до высоты 125 000 фут (38 км).
Хотя в действительности сопротивление будет возникать и до этой высоты, но предположим в запас прочности, что парашют начнет лишь на ней впервые испытывать сопротивление.
Скорость падения на этой высоте будет
* Пример благополучного спуска аэроплана, полетный вес которого (с пилотом и снаряжением) был 740 кг, на землю при помощи парашюта был сделан в 1926 году в морской воздушной станции в С. Диэго (С. А. С. Ш.). Пилот остановил мотор на высоте 750 метров над землей, и аппарат начал падать вниз в течение 1½ минут с начальной скоростью около 11 м/с. Парашют, прикрепленный к аппарату, немедленно раскрылся, и аппарат благополучно спустился на землю, ударившись о нее со скоростью около 6 м/с. Хотя при этом было поломано шасси, однако опыт этот был признан удачным.
Хотя подъем и спуск ракеты происходит весьма быстро (подъем на 370 километров в 6½ минут), однако необходимо следить за ее движением для чего желательно, чтобы она оставляла дымовой след в воздухе днем, или светящийся — ночью. Ящик с инструментами должен давать при падении на землю длительный черный дым.
Годдар считает возможность столкновения ракеты с метеорами „видимых“ размеров ничтожной, т. е. пренебрегаемой. Эта возможность может быть найдена из расчета вероятности столкновения сферы с частицами, движущимися случайно с постоянной скоростью и в предположении, что скорость сферы мала сравнительно со скоростью частиц.
Эта вероятность определяется следующим образом:
Пусть v — скорость сферического тела;
V — „ метеора;
n — число метеоров на единицу объема; это число выражается дробью, (взаимными столкновениями метеоров мы пренебрегаем);
S — площадь поперечного сечения сферического тела. Для v = 0, метеор, сталкивающийся с телом в промежуток времени от t до t+dt, пройдет путь от сферической границы радиуса Vt до v(t+dt) (пренебрегая диаметром тела). Далее, вероятное число метеоров в каждом малом объеме внутри сферической границы, путь которых направлен на столкновение с телом, равно
Для V=0 получается подобное же выражение для вероятного числа метеоров в объеме пространства, пронизываемого сферическим телом.
Если, по Ньютону, принять среднее расстояние между метеорами в 250 миль (470 км), а скорость их 30 миль/с (56 км/с), то при сферическом теле диаметром в 1 фут (0.305 м), движущемся со скоростью 1 миля/с (1855 км/с), на расстояние 220 000 миль (400 000км), вероятность столкновения будет 1,23·10-8, которой можно пренебречь.
Если тело падает в поток метеоров, то вероятность столкновения уменьшается, когда направление движения тела совпадает с таковым же метеоров.
Если v и V обе отличаются от нуля, то метеоры, попадающие в тело, летят как бы от сферической границы возрастающего радиуса Vt, подвижной центр которой отстоит на vt вперед от начального положения тела.
Если v мало отличается от V, то относительная скорость тела и метеора будет настолько мала, что ею можно пренебречь. Вероятность столкновения будет немного больше, если метеоры будут диаметром несколько сантиметров.
По мнению профессора Граффса (Гамбург) вероятность столкновения космического корабля с метеоритом весьма мала, так как число их на единицу объема пространства ничтожно, и аналогично одному грамму массы на объем в 100 куб. км (Scneiner-Graff: Astrophysik, 1922, .S. 305-306).
Далее К. Мейер в своей статье „Kometen und Meteore“ (Штуттгардт) стр. 68, пишет, что в потоке Леонид 1866 года, в наиболее густом месте его, метеоры отстояли на 110 км.
В русской и иностранной прессе часто появлялись заметки о работах Годдара. Не ручаясь за их достоверность, мы все же приводим содержание этих заметок.
В журнале „Эхо“ 1923 г. (5?) № 7 помещено краткое описание и рисунок (фиг. 16) проекта пассажирской ракеты, приписываемой Годдару, предназначенной будто бы для сообщения с Марсом. Наверху находятся буфера, смягчающие удар при спуске. В середине — вращающийся свободно — шар, где помещаются пассажиры; там есть каюта и комната для наблюдений.
 Фиг. 16. Пассажирская ракета, приписываемая Годдару. |  Фиг. 17. Межпланетный радиопередатчик, приписываемый Годдару. |
В 1925 г. в „Вестнике Знания“ (№ 8, стр. 581) была помещена заметка В. А. о проекте Годдара радиосигналов с ракеты на землю (фиг. 17).
По этому проекту ракета снабжается радиотелеграфным передатчиком, автоматически подающим сигналы во время полета. Ракета представляет собою стальной снаряд, длиною около 20 метров, разделенный на две части изолирующим кольцом. Верхняя часть его служит антенной, а нижняя — противовесом радиопередатчика. Предполагается, что при приближении к пределам земной атмосферы ракета начнет автоматически подавать радио-сигналы. Земные радио-станции таким образом смогут непосредственно убедиться, как распространяются радио-волны, приходящие извне.
 Фиг. 18. Ракетная торпедо-бомба, приписываемая Годдару. |
Хотя с 1926 года о дальнейших работах Годдара не появлялось в печати сведений, однако, повидимому (по мнению немецких техников), он продолжает работы, но уже для военного ведомства С. А. С. Штатов и сооружает ракетные торпеды-бомбы, при помощи которых из Америки можно будет бомбардировать Лондон, Париж и Берлин. На фиг. 18 показан вид подобной ракеты (по Гейлю).
На выставке межпланетных аппаратов в Москве в 1927 г. была представлена модель первоначально предположенной им большой составной стальной ракеты 1919 г. (фиг. 19, на стр. 134) с топливом в виде спирта, разбавленного водою, который, сгорая, поднимает ракету на некоторую высоту. Далее сжигается жидкий водород в сфере кислородной струи во второй ракете, находящейся в общем корпусе. После работы этих двух ракет их оболочки отпадают и далее летит лишь головная часть, заряженная бездымным порохом — нитроцеллулозой. Позднее Годдар отказался от жидкого топлива и от пассажирской ракеты и перешел на сухое топливо.
В своих позднейших опытах Годдар перешел опять на жидкое топливо [бензин + О2 (жидкий)]. Опытные ракеты его цилиндрические с конической головкой и с оперением из четырех плавников.
Под таким названием описан опыт Годдара над полетом его ракеты в журнале „Бюллетени американского межпланетного о-ва“.
В 1928 г. Годдар усовершенствовал дюзу своей ракеты и определил опытным путем состав смеси жидких водорода и кислорода. До своего основного опыта он произвел ряд предварительных опытов в Auburn'e ;(Массачуз.). Когда эти опыты дали удовлетворительные результаты, он перенес работу в Ворчестер, где была установлена ракета с барометром и парашютом. Здесь и произошел опыт под названием „Выстрел 17 июля“.
Годдаром была построена стальная башня высотою 12 метров (40 фут.); от основания башни к ее вершине вели рельсы для подъема ракеты. Размеры последней были: длина 2.74 м. (9 фут.) и диаметр 0.71 м. (28 дм). Взрывы должны были происходить с перерывами, а не непрерывно. Когда произошел взрыв, он был слышен за 3 км. Опыт дал блестящий успех. Хотя подъем был не велик, но парашют благополучно спустил оболочку и барометр.

Главнейшим результатом этого опыта была финансовая поддержка в работах. С 1919 по 1929 г. Смитсонианский институт истратил на опыты, не считая средств, израсходованных самим Годдаром, 12 000 долларов. В июле же 1930 г. из фонда Д. Гуггенгейма было предоставлено на продолжение опытов 100 000 долларов. В связи с этим начата постройка большой ракеты с приспособлениями для устойчивости, для спуска и с камерой для инструментов. Подъем предположен на высоту от 75 до 300 км. Опыты намечено произвести близ Розвелля (Нов. Мексика), где имеются более хорошие атмосферные условия, чем в Ворчестере.
Профессор Годдар в Америке вычислил, что при самых неблагоприятных условиях необходимо затратить следующие количества кг пороха на подъем каждого килограмма пустой ракеты:
| Порох кг 12.5 89 167.7 802 | Высота подъема километры. 55 368 693 За пределы земного притяжения. |
 Фиг. 20. |  Фиг. 21. Приписываемая Годдару ракета для полета на Луну. |
В одной из газет был помещен рисунок ракеты, которую будто бы спроектировал Годдар для полета на луну, причем эта ракета и должна была дать при падении на луну вспышку, видимую с земли. На фиг. 21 (стр. 135) изображены детали этой ракеты и приведены к ним пояснения.
Параллельно со своими теоретическими и экспериментальными работами Годдар сделал ряд изобретений, относящихся к улучшению обыкновенных ракет, причем им был взят ряд патентов на эти изобретения. Ниже мы приводим чертежи и краткие описания этих запатентованных ракет, заимствованные нами из сборников американских патентов (United States Letters Patent).
Вся ракета состоит из двух ракет: нижней большой и верхней — малой. Каждая из этих двух ракет имеет камеру сгорания с взрывчатым веществом и конусообразную дюзу, длина которой не меньше тройного наибольшего ее диаметра. Сверху нижней ракеты имеется труба, в которую вставляется верхняя ракета, вылетающая из этой трубы по прекращении действия взрывов в нижней ракете. Для устойчивости полета ракете придается вращение при помощи взрывов в искривленных горизонтальных каналах, расположенных в ее головке.
Взрывы производятся посредством последовательной подачи к дюзе патронов, спускающихся сверху вниз. Взорванные патроны удаляются в особую камеру внутри ракеты.
Взрывы производятся посредством последовательной подачи к дюзе патронов, спускающихся сверху вниз. Взорванные патроны посредством особого механизма удаляются от камеры сгорания и выбрасываются наружу через специальное отверстие.
 Фиг. 22. |  Фиг. 26. |
Подача патронов к дюзе производится автоматически вдоль ракеты, уборка их открытие и закрытие камеры, где взрываются патроны, производится пружинным механизмом. Использованные патроны выбрасываются наружу.
Если мы заставим, находящееся под влиянием силы земного притяжения и сопротивления воздуха W, жесткое тело с мгновенной (вообще переменной) массой М вертикально подниматься силой реакции струи газа (то есть ракету), то, согласно основному закону Ньютона и закону сохранения массы, мы можем написать дифференциальное уравнение
При последующих расчетах мы вводим следующие упрощения: 1) в виду подъема всего на 100+200 км полагаем g= const.; 2) при расчете воздушного сопротивления W, пренебрегается влиянием струи отброса; 3) пренебрегаются изменения величины импульса внутри ракеты из за изменения площади горения (в случае пороха и т. п.) и прочие подобные мелкие явления и 4) пренебрегается вращением земли.
Мы вводим следующие обозначения: Ме = конечная масса (то есть масса пустой ракеты) и Ма = начальная масса, откуда получаем массовое отношение q = (Ma — Ме) : Ме. Мы задаемся целью при заранее заданных условиях: Ме, полной высоте подъема h, начальной скорости ua при ta=0 и sa =0 и С = const (постоянная относительная скорость отброса)* определить минимальное значение Mа, то есть минимальное количество горючего (а отсюда и величины q).
Эта задача была поставлена американским профессором R. H. Goddart'oм**, давшим и попытку ее разрешения — однако, математически, весьма сомнительным путем. Мы дадим здесь решение этой задачи пользуясь методами вариационного исчисления.
* Условие С = const (пост. относ. скорость отброса) впервые указано К. Э Циолковским — оно является фундаментальным.
** A Method of Reaching Extreme Altitudes. Washington. U. S. A. 1919. Publication of the Smithsonian Institute.
Принимая уравнение (1) за линейное дифференциальное уравнение относительно М, мы можем его интегрировать и решить относительно Ма подстановкой конечных (в смысле конца процесса подъема) значений и получим
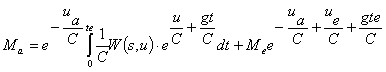 ........(2)
........(2)Значения te, uе, se относятся к моменту окончания взрывания т. е. к начальному моменту подъема по инерции, причем очевидно : se< h, где h обозначает полную высоту подъема. Так как я исследую проблему одной ракеты (без катапультирования т. е. без начальной скорости), то полагаю uа = 0. Однако, это условие имеет последствием отсутствие собственного минимума; имеется лишь нижний предел (граница), к которому однако можно приблизиться до любой степени, стоит для этого лишь дать скорости и быстро увеличиться от значения uа = 0 (при ta = 0) до определенного значения. В дальнейшем мы будем подразумевать под „минимумом“ этот нижний предел, который и есть настоящий минимум. Значит пред нами проблема следующего рода
 ........(3)
........(3)Мы получим, благодаря малой величине воздушного сопротивления при больших значениях величины h и s, приблизительно
Таким образом мы должны принять еще во внимание пограничное условие uе = ψ (se). Подставляем это выражение сразу в функцию F, так что добавочный член (слагаемое) будет иметь форму F [ψ (se), te].
Однако при подыскивании минимума значения Ма мы не имеем права пользоваться в интеграле подстановкой пограничного условия, так как известно, что у предельных значений функции пограничного условия ψ (se всегда можно подставить другое значение uе; от него величина интеграла может в любой малой степени измениться.
Значит интеграл уравнения (3) должен стать при определенных значениях se, te минимумом.
Это является обычной проблемой вариационного исчисления, оно соответствует уравнению Эйлера и дает регулярные предельные значения без сопряженной точки. Далее мы имеем при следующих всегда выполненных условиях
Таким образом интеграл дает сам по себе значительный минимум. Трудности возникают лишь при вариировании se и te или se и ue. При этом получаются следующие результаты :
1) Существует лишь одна единственная стационарная точка se = s0, ue — u0, при которой соблюдено условие (дМа : dse) = 0 и (дМа : дte) = 0. Она расположена на кривой u = ψ (s), так что эта конечная (или концевая) точка (условие) является в смысле courant'a естественной.
2) При вариировании величин 3) При любой вариации дискриминент членов второго порядка
 ........(9)
........(9)4) Однако такая остриеобразная область может лишь извне достигать кривую u = ψ (s).
Но эти внешние точки не имеют, как конечные значения se, ue, физического смысла, так как в этом случае торможение скорости ракеты должно было бы произойти посредством внезапного увеличения ее массы, что физически невозможно. Минимум обеспечивается математически неравенствомТаким образом существует настоящий минимум. При числовом расчете мы приняли для воздушного сопротивления формулу
 ........(11)
........(11)| Примечание. Труд этот опубликован в немецком журнале „Zeitschrift für angewandte Mathematik und Mechanik“ том 7, тетрадь 6, ноябрь — декабрь 1927 г. стр. 451 — 452. |