В 1928 г. в № 8-10 журнала „Die Rakete“ была помещена статья Р. Эсно-Пельтри (Перевод с франц. И. Винклера). Позже эта статья вошла в сочинение Э. Пельтри „ L'Astronautique“, Paris, 1930. Далее мы помещаем перевод этой статьи.

Н. Рынин.

Мои исследования вопроса о космических полетах показали, насколько они являются мало вероятными, пока мы будем располагать лишь существующими, известными нам, химическими реакциями для получения требуемой энергии. Иначе будет обстоять дело, когда физики предоставят в наше распоряжение внутриатомную энергию.

Прогресс науки заставляет меня заняться рассмотрением, как влияет новая теория на силу обычного действия, и я применю для этого математический анализ.

Пусть первая система (0), соединенная осями с наблюдателем, будет обозначена без значка, вторая же система, движущаяся по отношению к первой, обозначена значками (1).

Оси направлены обычным образом и могут вначале совпадать, t = t¹ = 0; х — х¹ = 0. Скорость, с которой система (1) движется относительно системы (0), направлена по ОХ и так, что оси ОХ и ОХ¹ при продолжении покрывают друг друга.

Пусть в момент t корабль движется со скоростью v в направлении положительных х, а система (1) имеет равную и постоянную скорость.

Пусть теперь в системе (1) находится материальная точка, неподвижная в момент t. Ее массу обозначим m₀. Приложим к ней силу, которую в системе (1) обозначим через F¹ и которая направлена в сторону положительных х и x¹. Тогда в системе (1) будем иметь

Пишем уравнения преобразования по Лоренцу

	............	(1)
y1=y	............	(2)
z1=z	............	(3)
	............	(4)
	............	(1')
y = y1	............	(2')
z = z1	............	(3')
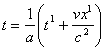	............	(4')

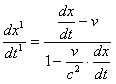.............(5)
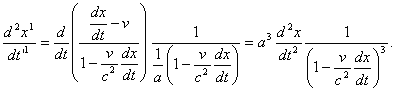.............(6)

Рассматривая движение в течение бесконечно малого промежутка времени dt, непосредственно следующего за t, будем иметь с приближением (до беск. мал.)

.............(7)

.............(8)

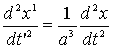.............(9)

Допустим, что пилот из физиологических соображений, допускает постоянное ускорение g (силы тяжести). Для упрощения расчета предположим, что реактивный прибор так урегулирован, что

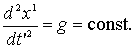.............(10)

Пусть корабль взлетает с земли с ускорением 2g, т. е. при ощущении человеком удвоенного веса.

Тогда из (9) имеем

.............(11)

Этого достичь всегда возможно, так как dt можно принять любым весьма малым. Переходя к пределу, видим, что отношение (11) остается справедливым в любой момент, если система (1) соединена с кораблем.

Так как теперь , то из (4) и (4') имеем

.............(12)

Но а — есть функция t, поэтому

.............(13)

Далее имеем для рассматриваемой системы при постоянном ускорении (g) в этой системе

.............(14)

Принимая при начальных условиях , получим, что для t = 0, постоянная интегрирования также равна 0. Поэтому, когда система соединена с ракетой, так, что то

Из (8) имеем

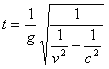.............(16)

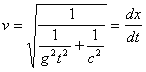.............(17)

Из последнего уравнения имеем

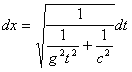.............(18)

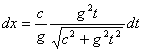.............(19)

При начальных условиях х=0 и t = 0

.............(20)

Из (8) и (17) имеем

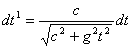.............(21)

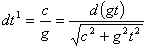.............(22)

При начальных условиях t¹ = 0 имеем для t = 0

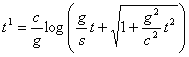.............(23)

Проверка. Элементы расстояния в космосе в обеих системах должны иметь одно и то же значение, что приводит к тому, что

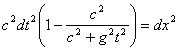.............(26)

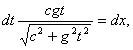.............(27)

Предположим теперь, что пилоты не знают законов относительности. Им известно лишь, что у них ускорение g= const., и они думают, что их движение следует закону

.............(28)

Для перелета расстояния X им кажется, что нужно время

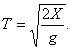.............(29)

При достаточно длинном пути, они думают, что в течение времени t¹=c/g (например в год т.е. в 354.2 дня при g = 981 С. G. S.) они достигнут скорости света и даже превзойдут ее.

В действительности же по уравнению (20) в системе наблюдателя время их будет

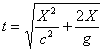.............(30)

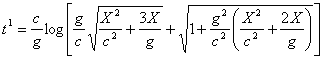.............(31)

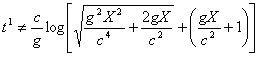.............(32)

Поэтому отношение действительного в их системе и кажущегося им времени будет

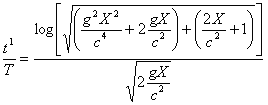.............(33)

Если Х весьма велико, то

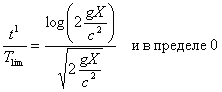.............(34)

Наоборот, если Х приближается к 0, то

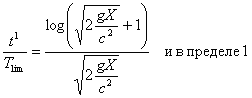.............(35)

Достойно внимания то, что кажущаяся продолжительность путешествия в системе пилотов будет меньше, чем это получается по данным классической механики, когда скорость полета превосходит скорость света и разница тем больше, чем длиннее и продолжительнее полет.

Для упрощения расчетов примем за единицу длины

Сравним различные времена, которые потребуются для покрытия известных расстояний в системе наблюдателя, от которого отправляются пилоты

Обозначим через

Т (форм. 29) — время, которое они измерили бы, если бы не знали законов теории относительности.

t — время, которое будет по их мнению в системе, соединенной с наблюдателем.

t' — время, которое они считают в системе своего корабля.

Все эти времена, считаются в тропических годах и имеют 3,1556·10⁷ секунд.

Эти числа указывают на изумительный выигрыш времени не только в системе 0, но в Евклидовской системе, при допущении, что скорость полета превосходит скорость света.

Таким образом при получении скорости в пространстве получим и скорость во времени, однако это возможно лишь в будущем.

Пусть система наблюдателя совпадает теперь с системой корабля, и движущаяся система с начала движения соединена с определенным атомом (электрон или ядро). Тогда можно применить уравнение (13), и тяга в системе корабля для каждого момента имеет выражение

.............(13)

Обозначим через v конечную скорость частицы при извержении из мотора и определим, какова будет ее работа; тогда можно рассчитать и тягу, сообщаемую ею кораблю в любой момент.

Пусть между плоскостями А и В дюзы во время t заключено число атомов ν по нормали к направлению движения неподвижных по отношению к мотору.

Плоскость А пересекается частицами с весьма малой скоростью. В плоскости же В частицы получают скорость извержения v.

Во время t+dt частицы находившиеся ранее между А и В передвинутся к бесконечно близким к ним плоскостям А¹ и В¹. При установившемся движении, число атомов между плоскостями А¹ и В будет постоянным, количество движения ее также будет постоянным. Число же атомов между А и А¹ и В и В¹ не одно и то же.

Обозначим их общую массу в покое δ m₀.

Процесс протекает так, как будто эта масса m₀ в промежуток времени dt обладала бы по отношению к скорости v скоростью = 0. Тогда количество движения не зависело бы от закона F=f (t). Поэтому его можно вычислить по формуле (13), полагая F= const, и равным его среднему значению. Суммирование для элемента времени t и в предложении

.............(13a)

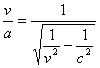.............(36)

.............(37)

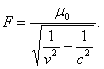.............(38)

Величина излученной энергии, по классической формуле, равна

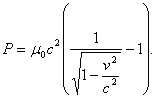.............(39)

Определим теперь энергию, необходимую для получения единицы реактивной силы. Она будет

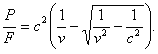.............(40)

Эта формула показывает, что если скорость изменяется от 0 до с, а извергаемая масса μ₀ постоянна, то сила растет от 0 до ∞ и частное растет от 0 до с.

Реакция благодаря извержению энергии.

По классическому уравнению

Это есть верхняя граница для случая извержения частиц.

Извержение материи. По уравнению (38) имеем

.............(42)

.............(43)

.............(44)

.............(45)

Из этого видим, что в случае материи, когда v изменяется от 0 до с, величина извержения, необходимого для получения единицы силы, изменяется от ∞ до 0. В случае же извержения энергии она равна постоянной величине , каковая значительно ниже скорости электронов радиоактивных тел и еще ниже получаемой при α-лучах.

Пусть m₀ масса корабля в его собственной системе, т. е. его масса в покое; начальная же его масса пусть будет М₀. Условие постоянства ускорения в системе корабля напишется в виде

.............(46)

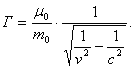.............(47)

откуда

.............(48)

Расход массы при полученной энергии будет по (44) и (39)

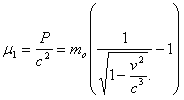.............(49)

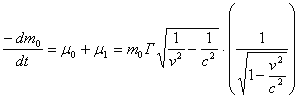.............(50)

.............(51)

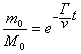.............(52)

Извержение только энергии. По уравнениям (46) и (45) имеем

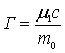.............(53)

.............(54)
.............(55)

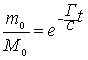.............(56)

Таким образом расход материи при извержении последней всегда значительно больше, чем при извержении энергии и они сравнялись бы, если скорость извержения материи достигла бы скорости света.

Вычислим величину отношения для этого предельного случая потребления и при различных дальностях. Не забудем, что t в уравнении (56) обозначает местное время корабля, и оно названо через t¹ в уравнении (32). При подстановке имеем

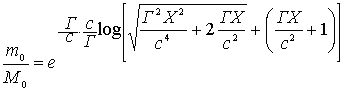.............(57)

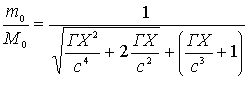.............(58)

Примем, как и раньше за единицу длины ; тогда получим

.............(59)

	=0.01	0.02	0.05	0.1	0.2	0.5	1
	=0.868	0.819	0.730	0.642	0.537	0.382	0.218

Если пилот покрыл данное расстояние и хочет далее тормозить, чтобы аннулировать скорость, то он должен повернуть аппарат и проделать все операции в обратном смысле.

Для полета туда отношения масс будут

	=0.02	0.04	0.01	0.22	0.4	1	2
	=0.753	0.671	0.533	0.412	0.288	0.146	0.0718

При полете туда и обратно, когда в конце полета туда не делается нового запаса горючего

	=0.02	0.04	0.1	0.2	0.4	1	2
	=0.567	0.450	0.284	0.170	0.0829	0.213	0.00515

Ближайшая звезда α Центавра удалена на 4.5 L, а Сириус на 10 L; поэтому в отношении этих звезд полученные результаты не очень утешительны.

Если же рассматривать Нептун, то он удален от солнца на 4.905·10^-14 L, и в этом случае, при полете к нему с ускорением в первой половине пути и с замедлением во второй, потребуется горючего 0.0434 М₀. Если же ускорение было бы постоянным, то время полета равнялось бы 3 дням 12 час. при скорости 3000 мм/с и горючее = 0.039 М₀.

Эти рассуждения побуждают произвести исследование, когда корабль движется ускоренно до достижения известной скорости, но такой, при которой продолжительность путешествия в системе корабля, была бы возможно меньше. Обращаясь к уравнениям (8), (12) и (17), получим

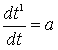
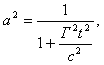.............(60)

.............(61)

Далее, принимая во внимание уравнения (52) и (23)

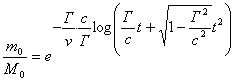.............(62)
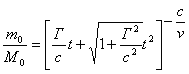.............(63)

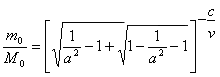.............(64)

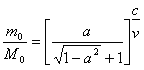.............(65)

При

=0

Интересно то, что это выражение не зависит от Г, т. е. не потребуется добавочных расходов, если корабль полетит с ускорением бóльшим g.

Полет тогда, без увеличения расхода горючего, выиграет время за счет увеличенной скорости, конечно, если организм человека выдержит перегрузку.

Числовые результаты, полученные из (65), указывают однако, что даже в наилучшем случае, когда v = c, имеем

a=0.5		0.2	0.1
	=0.268	0.102	0.050

Таким образом, используя внутриатомную энергию, мы можем сравнительно легко достичь пределов солнечной системы; что же касается до посещения других солнечных систем, то здесь, ввиду громадных, отделяющих их расстояний, нет надежды на успех.

Однако, нельзя ставить границ человеческому знанию. Может быть физиология даст средства удлинить жизнь, обновить организм и тогда поставленная нами задача будет решена.