Jj	— участки траектории ракеты, на которых она функционирует, т. е. сообщает себе ускорение;
Wу	— „скорость улета“ для данного состояния ракеты — та скорость, на которую нужно увеличить имеющуюся скорость ракеты, чтобы она приобрела движение по — параболической орбите относительно центра Земли;
Wв	— „скорость возврата“ для данного состояния ракеты — та скорость, которой ракета обладала бы, когда, продолжая двигаться по своей орбите, она достигла бы земной поверхности (уровня моря);
W	— „полная скорость улета“ и „последующая скорость возврата“, равная Wy, вычисленной для состояния неподвижности на уровне земной поверхности, равной Wв, вычисленной для состояния неподвижности в бесконечном удалении от Земли, или для ракеты, движущейся по параболической орбите равной „параболическая скорость“ (где R — радиус Земли, a g — ускороние силы тяжести на Земле) — 11 185 м/сек;
V	— скорость ракеты относительно центра Земли (а не земной поверхности) в данный момент;
r	— расстояние от ракеты в данный момент до центра Земли;

Под «полетом» мы будем подразумевать движение ракеты до некоторой, бесконечно удаленной от Земли, точки и возвращение обратно, причем скорости ракеты у точки назначения и у земной поверхности должны быть равны нулю. Мы будем пока игнорировать сопротивление атмосферы и присутствие в пространстве иных тел, кроме Земли, так что наши выводы этого параграфа будут приблизительно верны лишь для участков траектории, лежащих вне атмосферы ощутимой плотности, не приближающихся к Луне, и для траекторий, размеры которых значительны в сравнении с радиусом земной орбиты.

Нетрудно видеть, что для каждого состояния ракеты мы будем иметь:

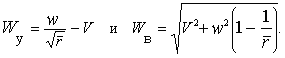(8)*

Для ракеты в состоянии спутника Земли с круговой орбитой

* Формула, которую приводит автор , может быть получена при условии, что параболическая скорость совпадает с направлением круговой скорости. Под V надо понимать . В этих условиях W_y будет равна приведенной автором скорости. В случае, если параболическая скорость не совпадает с направлением круговой скорости, то где γ — угол между направлениями параболической и круговой скоростями. Скорость возврата преобразовывается в , если положить и (Прим. ред.).

В том случае, когда орбита не касается и не пересекает земной поверхности, как, например, всякая круговая орбита, наше определение величины W_в является фиктивным. В подобных случаях под W_в мы должны разуметь ту скорость, которою ракета обладала бы, если бы к живой силе ее движения была прибавлена энергия, обусловленная ее массой и разностью потенциалов силы земного тяготения между точками ее пребывания в данный момент и точкой на уровне земной поверхности, вне зависимости от того, может ли это суммирование энергий произойти в действительности при движении ракеты по данной ее орбите или нет. Нетрудно затем видеть, что W_y имеет различные значения для различных удаленных от Земли точек одной и той же орбиты (если только орбита не параболическая, для которой М_у=0); наоборот, W_в имеет постоянное значение для всех точек одной и той же орбиты. Величины W_y и W_в имеют для нас следующее значение:

1) W_y, взятая для перигея (ближайшей к центру Земли точки орбиты), есть теоретический минимум W (т. е. вычисленный лишь на основании закона сохранения энергии), необходимый для того, чтобы двигающаяся по данной орбите ракета приобрела движение по параболической орбите, следуя по которой ракета может выполнить первую половину «полета» — движение до бесконечно удаленной точки;

2)W_в есть теоретический минимум W, необходимый для того, чтобы двигающаяся по данной орбите ракета достигла земной поверхности с нулевой скоростью и тем завершила вторую половину полета.

Для доказательства первого положения мы сравним между собою W_y1 и W_y2, вычисленные для двух точек а₁ и а₂ одной и той же орбиты, разность между потенциалами силы земного тяготения в которых равна бесконечно малой α. Если для более далекой из точек — точки а₁, — мы имеем по формуле (8)]

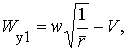
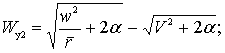
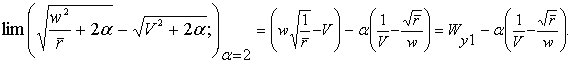
Примечание редактора первого издания. Так как при эллиптических скоростях

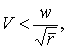
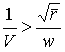
Таким образом по абсолютной величине, которая нас сейчас только и интересует, W_y2 < W_y1. Следовательно, W_y имеет минимум в точке перигея данной орбиты, который и является теоретическим минимумом ракетной скорости, необходимой для перехода на параболическую орбиту, что и требовалось доказать.

Для доказательства второго положения мы сравним между собой W_в1 и W_в2, получающиеся в двух случаях: в первом ракета, двигаясь по некоторой орбите, получила приращение скорости u в точке а₁; во втором, двигаясь по той же орбите с тою же скоростью, ракета получила той же величины отрицательное приращение скорости в другой точке а₂, причем разность потенциалов силы земного тяготения между точками а₁ и а₂ равна бесконечно малой α. Если в первом случае мы по формуле (8) будем иметь

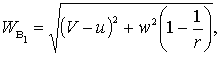
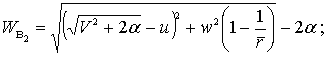
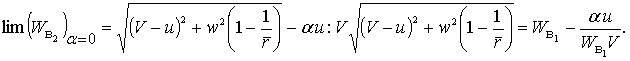
Таким образом W_в2 < W_в1 следовательно, мы получим тем меньшую W_в, чем ближе к Земле будут находиться точки, в которых ракета сообщает себе замедления. Минимум W_в мы получим, сообщая ракете отрицательные приращения скорости на уровне земной поверхности. Чтобы ракета завершила полет, мы должны погасить на уровне земной поверхности всю скорость, какой ракета будет обладать и которая будет равна W_в данной орбиты, что и требовалось доказать.

Оба предыдущие положения можно пояснить следующим образом.

Некоторый данный расход заряда ракеты сообщает ей некоторое определенное положительное или отрицательное приращение скорости независимо от состояния покоя или движения самой ракеты, но так как энергия ракеты относительно Земли — ее живая сила — пропорциональна квадрату ее скорости относительно Земли же, то некоторое данное приращение скорости представляет собою большее положительное или отрицательное приращение живой силы, тогда, когда оно происходит при большей первоначальной скорости ракеты; например, приращение скорости, равное 4, приложенное к скорости, равной 2, представляет собою приращение живой силы

Таким образом, с точки зрения энергии ракеты относительно Земли, реакция выделения действует на ракету тем сильнее, чем больше скорость самой ракеты. Но скорость свободно движущейся ракеты будет наибольшей в точке наибольшего приближения ее к Земле, следовательно, и действие реакции в этой точке будет наиболее выгодным как в тех случаях, когда необходимо сообщить ракете достаточную энергию для улета от земли, так и в тех, когда нужно лишить ее энергии для благополучного спуска на землю.

Таким образом мы видим, что W может достичь минимального значения 2w лишь при том обязательном условии (но еще недостаточном), чтобы все ускорения и замедления производились на уровне земной поверхности: поскольку это невозможно, W будет тем меньшей, чем ближе к уровню земной поверхности будут расположены J_j. Итак, близость к земной поверхности всех участков собственного ускорения ракеты J_j является первым требованием, какое мы должны предъявлять к траектории ракеты во избежание излишнего возрастания необходимой ракетной скорости — W. Разность W — 2w мы назовем «перерасходом ракетной скорости» и обозначим через Л. Под Л_i «перерасходом данного участка» — будем разуметь ту часть всего перерасхода Л_i, которая явились неминуемым следствием условий прохождения ракетой данного участка ее траектории. В общем случае

(9)

где V₁, V₂, r₁, r₂ — данные соответственно для начала и конца участка i. Верхний знак следует брать при „эллиптических“ скоростях ракеты

(10)

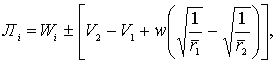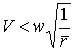
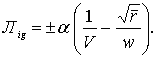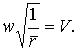
Вторым требованием, какое мы должны предъявлять к траектории ракеты для достижения возможно меньшего Л, является возможно меньший угол β между направлениями силы реакции и касательной к траектории. Абсолютное значение V изменяется в зависимости не от всего собственного ускорения ракеты j₀, а лишь от его тангенциальной слагающей, равной j₀ cos β; мы получаем, следовательно,

Л_iβ=W_i(1 — cosβ)(11)

Траекторию всего полета мы разделим условно на три участка.

1)Т_у — „траектория улета“ — участок траектории, начинающийся на земной поверхности и оканчивающийся в некоторой бесконечно удаленной точке;

2)Т_с — „связывающая траектория“ — участок траектории, начинающийся в конце Т_у и оканчивающийся в некоторой другой, бесконечно удаленной точке;

3)Т_в — „траектория возврата“ — участок, начинающийся в конце Т_с и оканчивающийся в точке на земной поверхности. Соответственно указанным обозначениям примем и обозначения W_yл, W_св, W_воз.

Обозначим:

Θ	— угол между траекторией в данной точке и плоскостью горизонта;
β	— угол между направлением собственного ускорения j0 и траекторией в данной ее точке;
λ = Θ + β	— угол между направлением j0 и плоскостью горизонта. Углы Θ и β считаются положительными, когда касательная к траектории направлена вверх от плоскости горизонта, а j0 направлено вверх от касательной к траекториии.

Смысл нашего деления траектории такой: в бесконечном удалении от земли сила земного тяготения ничтожна, а сопротивление земной атмосферы отсутствует. Вследствие этого Т_с поскольку она вся находится в бесконечном удалении от Земли, может иметь произвольную форму и при всякой форме ее может быть проделана ракетою со сколь угодно малыми j₀, V и W_св. Практически к Т_с можно приравнять участок траектории, находящийся от Земли на расстоянии нескольких десятков земных диаметров. W_св на практике определяется в значительной степени количеством времени, какое мы найдем удобным назначить для прохождения Т_с. Наоборот, Т_у и Т_в находятся своими частями в пределах сферы сильного тяготения и отчасти в пределах сопротивляющейся среды — атмосферы; поэтому та или иная величина W, а следовательно, и Л всецело зависят от той геометрической формы и тех скоростей, какие мы выберем для Т_у и Т_с в дальнейшем. Поэтому, разбирая различные типы траекторий, мы будем иметь в виду из них лишь участки Т_у и Т_в, оставляя в стороне относительно для нас неважную Т_с. Так как при отсутствии сопротивления среды тождественные по форме и абсолютной величине скоростей в соответственных точках Т_у и Т_в требуют для своего выполнения равных ускорений в соответственных точках, то и W_у и W_воз для этих Т_у и Т_в будут между собой равны. Приводимые ниже выкладки относятся поэтому одинаково к Т_у и Т_в, поскольку они лежат вне пределов атмосферы ощутимой плотности.

Нетрудно видеть невозможность построения такой траектории, которая одновременно вполне отвечала бы обоим изложенным выше требованиям (стр. 37 и 38) для достижения наименьшего перерасхода скорости Л. Типом траектории, вполне отвечающим „второму требованию“, является „радиальный“, Т_у и Т_в которого представляют собою продолжения земных радиусов. Согласно "первому требованию“, в радиальной трактории мы должны по возможности сократить J_j, сообщая ракете j₀ возможно большей величины, начиная от точки отправления и непрерывно до той точки, в которой ракета будет уже обладать параболической скоростью ; при возвращении с соответсвенной точки должно начинаться j₀ — „собственное замедление“ ракеты. Положим для упрощения, что ускорение силы тяжести на всем протяжении J_j таково же, как и на земной поверхности g.

Обозначим:

(12)*

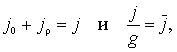
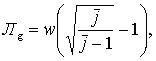* Формула (12) из формулы (9) получается следующим образом.

Полагая j= j₀ + j_ρ и g=g₀, можно написать

Так как , имеем .
Интегрируя при начальных условиях V=0 и r=R, имеем: но, так как W² = 2gR, то, заменяя V через W, получим: jr — jR — gr = 0; отсюда Но так как то, заменяя здесь r через имеем

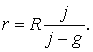
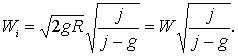
Теперь обратимся к формуле (9) и определим Л_g. Так как j₀ сообщается ракете непосредственно у земли, то g=g₀, V₂ — скорость ракеты в бесконечности и, следовательно, V₂=0; V₁ — скорость у земли так же равна нулю, r₂ = ∞, r₁ = 1, так как r₁=R в силу того, что скорость сообщается у Земли. Таким образом из сделанных предпосылок имеем Л_g =W_i — w. Но
следовательно,

или, вводя обозначение будем иметь: т. е. получили формулу (12).

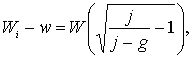
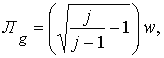
Разложение в ряд подкоренного выражения при условии j> > 1 приводит к выражению следующего вида: , а не к такому, которое приводит Кондратюк, т. е. 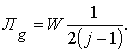. (Прим. ред.).

или, упрощая при j > > 1;

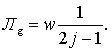
Типом траектории, отвечающим „первому требованию“, является „тангенциальный“ (фиг. 1): от точки отправления o до точки b ракета движется параллельно земной поверхности по дуге большого круга, горизонтальное движение ракеты достигается направлением j₀ под таким углом β к горизонту и траектории, чтобы сила Mj₀ sin β уравновешивала собою избыток силы тяжести ракеты над

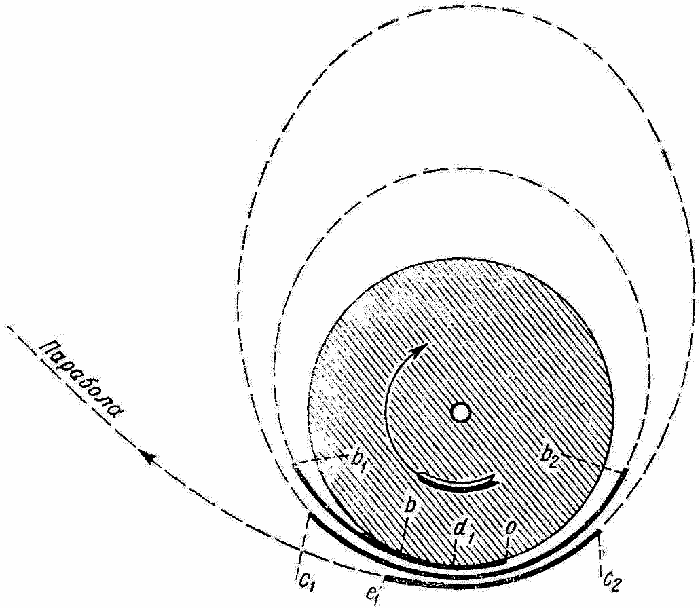Фиг. 1. Типы траекторий. Жирными линиями показана Ту, пунктирными — участки свободного полета по эллиптическим и параболическим орбитам.

ее центробежной силой; до точки d₁ угол β должен быть положительным, после же этой точки, в которой β делается отрицательным, так как центробежная сила будет уже превышать силу тяжести. Движение по кругу продолжается до тех пор, пока необходимый для его поддержания угол β, все увеличивающийся (по абсолютной величине) с возрастанием скорости и центробежной силы, не достигнет такой величины, что Л_β [формула (11)] станет ощутимо вредной частью перерасхода. По достижении углом β (соответственно скорости ракеты) такого значения ракета движется некоторое время при постоянном β, уже удаляясь от земной поверхности с все возрастающим углом Θ. Когда в точке b₁ становится практически вредной величиной и Л_g вследствие все возрастающей разности потенциалов силы тяжести между точкой нахождения ракеты в данный момент и перигеем той орбиты, по которой ракета получила бы движение, если бы j₀ было прекращено (о влиянии этой разности на W_y см. стр. 35), функционирование ракеты прекращается, и от точки b₁ до точки b₂ ракета свободно движется по эллиптической орбите. В точке b₂, симметричной точке b₁ (относительно большой оси эллипса), j₀ опять возобновляется при β < 0, чтобы J_j прошел возможно ближе к Земле, и продолжается до точки с₁, отвечающей тому же условию, что точка b₁ за точкой с₁ опять следует свободная эллиптическая орбита — с₁ — с₂, потом опять расположенный вблизи земной поверхности J_j = с₂ — е₁ и т. д., пока мы по прохождении последнего J_j не получим требуемых параболических скорости и орбиты: При тангенциальной траектории Л_gβ, который будет получаться после прохождения ракетою точки d₁ теоретически может быть сделан сколь угодно малым посредством достаточного сближения между собою точек d и b₁, b и b₁, b₂ и с₁, с₂ и е₁ и т. д., причем лишь будет увеличиваться число промежуточных эллипсов и продолжительность полета. Этой частью Л_gβ, как зависящей в значительной степени от нашего произвола, мы будем пока пренебрегать; наоборот, Л_β, получающийся до точки d₁ имеет определенный теоретический минимум, равный приблизительно (при j > > 1)

(13)

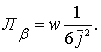Это приблизительное значение мы и примем для дальнейшего. Кроме меньшего более чем в 3 j раз перерасхода, тангенциальная траектория имеет еще и то большое преимущество, что, производя отправление и возвращение ракеты в экваториальной плоскости с запада на восток, мы, вследствие вращения Земли вокруг своей оси, получаем для всего полета экономию ракетной скорости W, равную удвоенной скорости движения земной поверхности:

Помимо трудности требуемого при тангенциальной траектории точного управления, она обладает еще одним недостатком, который делает применение ее в чистом виде при отправлении невозможной Т_у тангенциального типа требуют точки отправления вне атмосферы ощутимой плотности, так как в противном случае, вследствие большой длины участков, расположенных на уровне точки отправления и немногим выше ее, неимоверно возрос бы Л_с, во много раз перевысив собою экономию W, получающуюся от меньшего при тангенциальной траектории перерасхода Л_gβ и от утилизации скорости вращения земной поверхности. Практически наивыгоднейшим типом Т_у явится поэтому не тангенциальный, а некоторый компромиссный, начинающийся дугою спирали, примерно показанный на обложке. Угол Θ для этой спирали должен быть тем меньшим, чем меньше будет возможная величина j₀ (и чем больше для нас будет поэтому иметь значение Л_gβ) и чем меньшим будет замедление j_ρ, вызываемое сопротивлением атмосферы. Для этого среднего типа траектории Л_gβ будет иметь значение, среднее между

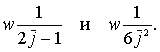
В дальнейшем мы будем считать, что при Θ < 30° и при j > 3, если ракета не пользуется авиационными крыльями, или j > 1, если ракета ими пользуется,

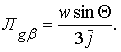(14)

при обязательном условии применения поддерживающих поверхностей авиационного типа, если только будет j < 2. Что касается Т_в тангенциального типа, то она применима в почти чистом виде и может дать очень большую экономию W_воз вследствие полезного для нас при возвращении сопротивления атмосферы, которое будет помогать гасить скорость возврата ракеты. Об этом будет сказано отдельно ниже — в гл. IX.

далее

назад