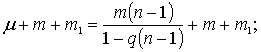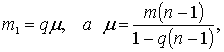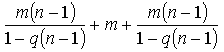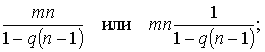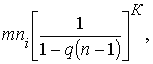В пассивных массах ракеты, т. е. в массах, не относящихся к топливу μ, мы можем различить две существенно различные части:

1) абсолютный пассив m, к которому относятся люди со всем необходимым для их жизни и выполнения заданной им операции и благополучного спуска на земную поверхность по окончании функционирования ракеты как таковой;

2) пропорциональный пассив m₁ — массы всех предметов, обслуживающих функционирование ракеты, к каковым относятся: а) сосуды для топлива, б) камеры сгорания, в) сопло, г) приборы и машины, перемещающие топливо в камеру сгорания, и д) все части, связывающие предметы первых четырех категорий и придающие прочность всей конструкции ракеты. Эту часть массы мы назовем «пропорциональным пассивом», ввиду того что по конструктивным законам он в общем должен быть по своей массе приблизительно пропорционален массе обслуживаемого им топлива, пока это последнее не превосходит некоторой величины; при больших значениях μ отношение растет. Исходной точкой конструирования ракеты является ее наперед устанавливаемый m, а с ним уже согласовываются μ и m₁; m остается постоянным все время полета; μ постепенно расходуется, а m₁ может быть изменяем при нашем на то желании, соответственно уменьшающимся массам топлива μ и расхода .

Обозначим отношение =q и предположим, что все время у нас функционирует один и тот же несменяемый пропорциональный пассив m₁. Тогда m₁=μq; М_к = m+m₁ = m+ μq. Подставив это значение М_к в формулу (26), получаем:

откуда

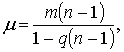(6)

Для того же чтобы масса ракеты не увеличивалась значительно из-за присутствия в ней масс m₁ и необходимости сообщать им скорость наравне с m, желательно иметь примерное отношение

***

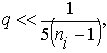(7)

* В самом деле формулу (6) можно представить в виде

следовательно, если то μ будет близкой к m (n-1). При увеличении q разность будет стремиться к нулю и μ → ∞ при условии функционирования одного и того же m₁ на всем полете.

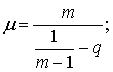
** Здесь речь идет об удвоенном μ по сравнению с μ при m₁ = 0.

*** Условие 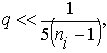показывает, что при выборе q в согласии с этим условием мы будем иметь значение μ, пропорциональное μ₀= m(n — 1) в следующей последовательности:

и чем выше значение К, тем ближе μ к μ₀. (Прим. ред.).

Принимая во внимание все утечки энергии и несовершенства, мы можем утверждать, что действительное значение n при W=22 370 м/сек будет не менее 100, а если мы захотим использовать топливо подешевле и применим частью углеводородные группы, то и более 100. Следовательно, при q= ¹/₉₉ масса топлива по формуле (6) уже превращалась бы в бесконечность, при g =¹/₂₀₀ удваивалась бы, между тем ¹/₂₀₀μ — это величина очень и очень тесная, вернее — вовсе невозможная для массы всего комплекта m₁. Даже если мы примем W=14 460 м/сек и возьмем соответственно n₂ = 20 (стр. 24), то и то получаем удвоение μ при трудно выполнимом отношении m₁ = ¹/₄₀ μ.

Практически наилучшей системой будет поэтому двухкомплектная для машин и приборов и трехкомплектная для

* Так как — , а М_iк включает в себя μ для i+1 участка, потому n_i=1 не лишено смысла. (Прим. ред.). сосудов, как более громоздких частей m₁. Если мы опять положим n= 100, то абсолютный предел q поднимается с ¹/₉₉ (при однокомплектной системе) до ¹/₉ при двухкомплектной и до при трехкомплектной системах*. Несколько-комплектная система хотя и дает бóльший простор в конструировании предметов m₁ и избавляет нас от провала всего предприятия из-за невозможности сконструировать достаточно легким m₁, но все же не совершенно ликвидирует вредное влияние масс m₁ на величину массы ракеты: значение μ по формуле (6) получается все же бóльшим того, какое бы мы имели при полном отсутствии m₁.

Если мы применим несколькокомплектную систему, разделив траекторию на несколько участков с равными W_i для каждого из них, то для всего полета получится увеличение массы в

(6а)

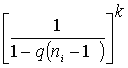
* Чтобы получить цифры, указанные Кондратюком, для двухкомплектной системы q = ¹/₉ и для трехкомплектной необходимо помнить, что автор каждому участку дает комплект, а каждый участок имеет одно и то же W_i, следовательно, для однокомплектной системы имеем W, для двухкомплектной системы имеем ½W= W_i и для трехкомплектной W_i⅓W. Так как , то для двухкомплектной и для трехкомплектной

Таким образом можно представить n_i — многокомплектную систему через n однокомплектных систем следующим образом:

Для трехкомплектной системы автор дает значение , а надо .

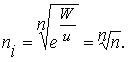
(Прим. ред.).

Примечание. Основание степени этой формулы мы получаем, если к правой части уравнения (6) прибавим m+m₁ и затем вынесем mn₁ за скобки¹.

Примечание редактора первого издания. В пределе при K = ∞ дробь в формуле (6) принимает значение:

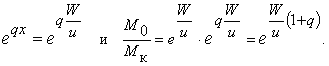
Можно предложить такое решение вопроса об m₁, при котором вредное влияние присутствия масс m₁ устраняется почти совершенно. Решение это заключается в следующем: как и при несколькокомплектной системе, конструируется несколько комплектов m₁ постепенно убывающей величины; материалом для конструкции служат по возможности преимущественно алюминий, кремний, магний; части, требующие особой огнеупорности (внутренняя поверхность камеры сгорания), делаются из подходящих сортов графита, карборунда корунда. Комплекты, становящиеся по своей величине излишними вследствие уменьшившейся массы ракеты, не отбрасываются, а разбираются и поступают в камеру пилота на переплавку и раздробление, чтобы затем быть употребленными в качестве химических компонентов топлива. Такое решение является идеальным, так как при нем в качестве вредных масс m₁ остается лишь последний, самый меньший комплект, все же предыдущие являются компонентами топлива, временно исполняющими функции m₁. Так как разборка и дальнейшее преобразование предметов m₁ требуют некоторого времени, то при такой системе деление траектории ракеты на участки, обслуживаемые бессменными комплектами m₁, уже не является произвольным: первая смена комплектов не может быть произведена ранее достижения ракетою состояния свободного спутника Земли; последняя смена не может быть произведена позднее того, как ракета при возвращении потеряет скорость настолько, что не сможет быть уже свободным спутником Земли. Этими двумя сменами удобнее всего и ограничиться, тем более, что они соответствуют делению траектории на три участка с приблизительно равными W₁ для каждого. Для разборки предметов m₁ в безвоздушном пространстве и преобразовании их в компоненты топлива потребуются некоторые добавочные приспособления. Тем не менее, следует приложить все усилия именно к такому решению вопроса об m₁ так как оно облегчает основную трудность всего предприятия, уменьшая необходимую массу ракеты, весьма большая величина которой лишь и является практически трудно преодолимым материальным препятствием к завоеванию межпланетных пространств и тел солнечной системы, что теоретически не представляет каких-либо особых трудностей.

¹ Запас топлива при m₁=0 по формуле (6) будет:

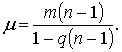
Полный вес, следовательно, будет μ+m, но так как при m₁=0 μ=m(n-1) то μ + m= mn.

Следовательно, сравнивая веса ракеты при m₁ ≠=0 с m₁ = 0, имеем:

но поэтому имеем: и после преобразования получаем: с другой стороны при многокомплектной системе n = n_i^К, поэтому можно написать:

далее

назад