академик, лауреат Ленинской премии
УПРАВЛЕНИЕ ДВИЖЕНИЕМ КОСМИЧЕСКИХ АППАРАТОВ
в приложении этого номера:
ХРОНИКА КОСМОНАВТИКИ
НОВОСТИ АСТРОНОМИИ

Издательство «Знание» Москва 1986
ББК 39.62
Р 26
На первой странице обложки: советская станция «Луна-3» – первый космический аппарат, использующий систему управления движением.
На последней странице обложки: схема движения советской станции «Луна-3» (см. текст).
СОДЕРЖАНИЕ
Введение3
Эволюция орбит6
Маневрирование в космосе17
Коррекция межпланетных траекторий. Гравитационный маневр27
Управление ориентацией36
Внешние моменты42
Сближение космических аппаратов49
Ручное управление54
Заключение57
Рекомендуемая литература58
ХРОНИКА КОСМОНАВТИКИ59
НОВОСТИ АСТРОНОМИИ63
Раушенбах Б. В.
Управление движением космических аппаратов. – М.: Знание, 1986. – 64 с, ил. – (Новое в жизни, науке, технике. Сер. «Космонавтика, астрономия»; № 3).
11 к.
Управление движением космических аппаратов ознаменовало собой важный шаг в развитии космонавтики. Лишь с разработкой методов такого управления представилась возможность осуществлять пилотируемые полеты, проводить запуски автоматических зондов к другим планетам и к Луне, решать многие народнохозяйственные задачи с помощью искусственных спутников Земли. Основы этих методов и излагаются в данной популярной брошюре.
Брошюра рассчитана на широкий круг читателей, интересующихся современными проблемами космонавтики.
3607000000ББК 39.62
© Издательство «Знание», 1986 г.
ВВЕДЕНИЕ
Говоря об управлении движением космических аппаратов, т. е. об осуществлении маневрирования их в космосе, коррекций траекторий межпланетных зондов, операций по сближению транспортного корабля с орбитальной станцией, нужной ориентации космического аппарата относительно внешних ориентиров и других аналогичных операций, следует прежде всего указать на своеобразие и резкое отличие космических условий от всего того, к чему мы привыкли в нашей повседневной земной практике.
Это отличие связано с практическим отсутствием внешней среды, в которой осуществляется движение, поскольку в космическом пространстве практически нет вещества. Это обстоятельство придает движению космического аппарата ряд почти очевидных, но тем не менее необычных свойств. Прежде всего следует отметить, что оно осуществляется в условиях, которые исключают наличие трения, аэродинамического сопротивления или других аналогичных явлений, что, в свою очередь, приводит к отсутствию у космического аппарата «естественного» торможения.
В земных условиях любое предназначенное для движения устройство (автомобиль, лодка), если его просто толкнуть, остановится довольно быстро. И это совершенно закономерно. Другое дело в космосе. Здесь сообщенный телу импульс или приращение скорости не будет гаситься силами сопротивления, и движение становится как бы вечным. Однако это не значит, конечно, что скорость и направление движения космического аппарата будут постоянными. Они могут изменяться, но эти изменения связаны с действием гравитационных сил.
При удалении от центра притяжения (например, планеты) скорость космического аппарата убывает, соответственно уменьшается и его кинетическая энергия, но возрастает потенциальная энергия, способная вновь превратиться в кинетическую. При сближении же с центром притяжения (при падении на планету) скорость космического аппарата будет возрастать в той же степени, в которой она убывает при удалении от центра притяжения (при подъеме с поверхности планеты).
Совсем иной характер имеет уменьшение скорости вследствие действия сил сопротивления среды. Здесь, как известно, кинетическая энергия тела переходит в тепло, которое уже не обладает способностью вновь перейти в кинетическую энергию движения тела. В этом случае потери кинетической энергии будут необратимы. И именно эти необратимые потери не проявляются в космическом полете.
Другим следствием отсутствия внешней вещественной среды является исчезновение возмущающих действий этой среды на движущийся космический аппарат. В обычной земной практике такие возмущающие воздействия играют нередко очень большую роль. Достаточно вспомнить, как влияют ветры, течения и бури на движение самолетов и морских судов. В космическом же полете подобного рода явления полностью исключены. Это приводит к существенному качественному изменению характера движения космического аппарата, так как его движение становится предсказуемым.
Действительно, если ракета-носитель разгонит космический аппарат до нужной скорости и придаст аппарату нужное направление, то все его дальнейшее движение после отделения от ракеты-носителя (при выключенных ракетных двигателях) произойдет по требуемой траектории. Если старт произведен не совсем точно (а ведь технические устройства всегда работают с некоторой небольшой ошибкой), то и здесь возможность прогнозировать движение космического аппарата весьма существенна.
Пусть, например, целью полета космического аппарата является достижение планеты Венера. Тогда, производя нужные измерения вскоре после старта, можно предсказать все дальнейшее движение, т. е. указать, где и когда произойдет встреча с планетой и является ли полученная траектория «попадающей» (достигнет ли посланный космический аппарат поверхности Венеры) или она проходит на каком-то расстоянии от планеты. На основании такого прогноза можно решить, следует ли исправлять полученную траекторию путем включения на короткое время корректирующего ракетного двигателя, а если это необходимо, то можно вычислить, когда и как это лучше сделать.
Ничего даже отдаленно похожего земная практика не знает. Немыслимо представить себе, что можно так «толкнуть» лодку в Одессе, чтобы она через несколько суток появилась в Сухуми. Даже если бы силы сопротивления воды не затормозили бы сразу ее движение, волны, ветер и течения увели бы лодку с заданной трассы далеко в сторону.
Наконец, отсутствие внешней среды приводит к еще одному специфическому эффекту: движение центра масс космического аппарата и вращение его корпуса вокруг центра масс оказываются «развязанными» друг с другом. Все мы привыкли к тому, что, глядя, скажем, на корабль, способны указать, куда он движется, поскольку нос корабля всегда направлен в сторону движения (если, конечно, не рассматривать случай, когда корабль идет задним ходом). То же можно сказать и относительно самолета или автомобиля. В земных условиях поворот рассмотренных транспортных средств вокруг центра масс сразу приводит к изменению направления движения самого центра масс.
Важно подчеркнуть, что привычное управление этими средствами происходит в результате взаимодействия движущегося тела (автомобиля, корабля, самолета) с внешней средой. Действительно, лишь сцепление колес автомобиля с поверхностью дороги приводит к тому, что поворот руля (а следовательно, и передних колес) вызывает изменение направления движения самого автомобиля. Достаточно нарушить это взаимодействие колес с внешней средой, как исчезнет и возможность управления автомобилем.
Если автомобиль попадет зимой на заледеневший участок дороги, сцепление колес с поверхностью дороги резко ослабнет и сразу окажется, что направление его движения больше не связано с поворотами руля. Автомобиль может продолжать двигаться вперед вдоль дороги (по прямой линии) и одновременно вращаться вокруг вертикальной оси. Этот своеобразный вальс является опасной аварийной ситуацией, хорошо знакомой водителям. С точки зрения механики такое движение можно охарактеризовать как происходящее без взаимодействия движущегося объекта с внешней средой (лед свел силу сцепления с грунтом к нулю), в результате чего движение его центра масс и вращение объекта вокруг центра масс оказались «развязанными».
Тип движения, который в земных условиях возникает крайне редко и то лишь как аварийная ситуация, является в космосе нормой. Траектория движения космического аппарата (с выключенными двигателями) не зависит от того, какова ориентация аппарата. Совершенно нормальным режимом полета является такой, при котором строгое движение по заданной траектории сопровождается беспорядочным «кувырканием» космического аппарата вокруг своего центра масс. Эта особенность космического полета позволяет рассматривать движение центра масс (т. е. изучать орбиты) независимо от рассмотрения вопросов ориентации, связанных с вращением космического аппарата вокруг центра масс. Возможность такого разделения сильно упрощает изучение механики космического полета.
Подводя итог сказанному, можно утверждать, что практическое отсутствие внешней среды придает глубокое своеобразие космическому полету. Движение в космосе не знает «естественного» торможения, связанного с рассеиванием механической энергии, оно происходит без внешних помех (поэтому существует возможность точного прогноза траекторий), а движение центра масс космического аппарата по траектории не связано с его вращениями вокруг центра масс.
ЭВОЛЮЦИЯ ОРБИТ
Задачи управления движением космического аппарата можно свести к трем основным типам:
1) получение нужной траектории (управление движением центра масс);
2) управление ориентацией, т. е. получение нужного положения корпуса космического аппарата относительно внешних ориентиров (управление вращательным движением вокруг центра масс);
3) случай, когда эти два типа управления реализуются одновременно (например, при сближении космических аппаратов).
Рассмотрение различных типов управления движением начнем с первого – с задачи получения заданной траектории полета.
Нужная орбита в основном формируется ракетой-носителем. Космический аппарат отделяется от ракеты в заданной точке пространства и с заданными величиной и направлением скорости. Однако и характеристики скорости, и точку отделения от ракеты-носителя нельзя реализовать абсолютно точно. Нужная скорость достигается лишь с некоторой технически возможной точностью, и эта технически неизбежная ошибка способна привести к недопустимым отклонениям траектории полета от расчетной. Так возникает задача коррекции орбиты, фактически приобретенной космическим аппаратом, и приближения ее к орбите, необходимой для выполнения задач полета.
Коррекция орбиты может потребоваться и тогда, когда выведение ракетой-носителем было осуществлено с требуемой точностью. На космический аппарат в течение долгого времени действуют малые силы (малые по сравнению с «обычной» гравитационной силой взаимодействия небесных тел), которые постепенно изменяют орбиту космического аппарата, происходит эволюция орбиты. После того как эволюция орбиты приводит к недопустимым отклонениям от заданной, возникает потребность в проведении коррекции.
Иногда маневрирование в космосе связано не с целью исправления ошибок выведения или последствий естественной эволюции орбиты, а с другими задачами: переходом на орбиту сближения с другим космическим аппаратом, на орбиту спуска на Землю и т. д.
Прежде чем обратиться к обсуждению задачи маневрирования в космосе (в частном случае – коррекции орбит), напомним основные определения и законы небесной механики. Как известно, при гравитационном взаимодействии двух небесных тел движение одного относительно другого происходит по эллипсу, параболе или гиперболе (их нередко объединяют в понятие конического сечения). Первый из названных случаев соответствует такому движению, когда небесные тела вращаются около друг друга на некотором конечном расстоянии. Два других случая характеризуют движение, при котором с течением времени расстояние между телами стремится к бесконечности, а сближаются они лишь однажды.
В космонавтике чаще приходится иметь дело с первым типом движения, носящим периодический характер, и поэтому все дальнейшее изложение (если не будет особо оговорено) будет исходить из предположения, что космический аппарат движется по эллиптической траектории относительно центрального небесного тела. Центральным небесным телом, в гравитационном поле которого движется космический аппарат, может быть Земля (в случае искусственного спутника Земли) или Солнце (при перелете автоматических зондов по трассам Земля–Марс, Земля–Венера и т. п., когда космический аппарат уже достаточно сильно удалился от Земли, но еще не приблизился к планете назначения). Центральным телом может быть и Луна, планеты или их спутники.
Рассмотрим сначала более распространенный случай: центральным телом, вокруг которого движется космический аппарат, является Земля. Само собой разумеется, что все полученные выводы будут справедливы и для других случаев.
Как уже говорилось, орбита, по которой происходит движение искусственного спутника Земли, является эллипсом. Но эллипс – это плоская фигура, поэтому можно ввести понятие плоскости орбиты (плоскости, в которой лежит упомянутый эллипс), проходящей через центр масс центрального небесного тела. Ее положение в пространстве является весьма важной характеристикой движения космического аппарата, и для определения этого положения достаточно знать два угла. Проиллюстрируем это, обратившись к привычным представлениям, связанным с географическим глобусом Земли.
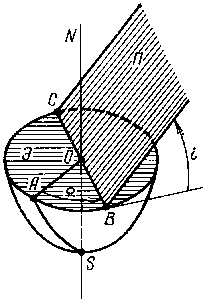 Рис. 1. |
На рис. 1 показана нижняя полусфера земного шара (отличием формы Земли от шарообразной здесь пренебрегается), причем показанная штриховкой плоскость Э представляет собой плоскость экватора. Меридиан SA будем считать нулевым (например, гринвичским). Плоскость орбиты П пересекается с плоскостью экватора Э по прямой ВС, проходящей через центр Земли О (чтобы упростить чертеж, на нем показан лишь малый участок этой плоскости), и наклонена к плоскости экватора под углом i (употребление в небесной механике латинских букв для обозначения углов вместо обычно используемых сейчас греческих – свидетельство о давнем происхождении этой науки).
Итак, с плоскостью П экватор пересекается в точках В и С. Поскольку космический аппарат вращается вокруг центра О, то он периодически оказывается то выше, то ниже плоскости экватора. Иначе говоря, он оказывается то в области пространства, где расположен Северный полюс, то в области пространства, где расположен Южный полюс, обозначенный буквой S. Если космический аппарат из нижней области попадает в верхнюю, с той стороны от центра О, где расположена точка В, то говорят, что точка В является восходящим узлом. Угловое расстояние восходящего узла от нулевого меридиана обозначается буквой Ω. Теперь мы видим, что положение плоскости орбиты искусственного спутника Земли полностью определяется заданием двух углов Ω и i.
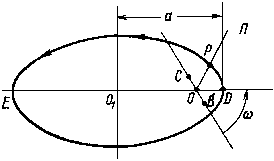 Рис. 2. |
Рассмотрим затем движение космического аппарата в плоскости орбиты П (рис. 2). Показанная здесь эллиптическая траектория движения характеризуется большой полуосью а, т. е. расстоянием от центра эллипса О1 до наиболее удаленной от него точки орбиты D, и эксцентриситетом е, характеризующим степень вытянутости эллипса. Последнее число можно представить как отношение двух отрезков: расстояния между центром и фокусом эллипса О1О и большой полуоси O1D. Для окружности е = 0, так как у нее центр и фокус совпадают. По мере увеличения вытянутости эллипса численное значение е будет возрастать, однако оно всегда меньше единицы. Ведь фокус находится внутри эллипса, и поэтому всегда O1O < O1D.
Таким образом, числа а и е определяют размеры и форму орбиты. Чтобы задать положение эллипса в плоскости П, необходимо указать еще одно число. Как известно, центральное небесное тело (в нашем случае Земля) располагается в фокусе орбиты, т. е. в точке О, как это показано на рис. 1. На рис. 2, кроме того, даны точки пересечения плоскости орбиты и линии экватора, также обозначенные буквами В и С. Очевидно, что полупрямая ОВ указывает, как и ранее, направление в сторону восходящего узла. Точка орбиты D является точкой наименьшего расстояния от фокуса О, ее обычно называют перицентром (или перигеем, если центральным телом является Земля). Угол между прямыми ОВ и OD, обозначенный через ω, и определяет положение большой оси эллипса, а значит, и орбиты в плоскости П.
Пять чисел Ω, i, ω, а, е полностью определяют геометрию движения космического аппарата. Если, помимо этого, нужно осуществить еще и привязку движения по времени, сделать возможным указывать момент времени и соответствующие точки траектории, то следует задать еще одно число. Обычно таким числом является момент времени τ, соответствующий «первому» прохождению космического аппарата через перицентр (точку D).
Понятие «первого» прохождения, конечно, условно. Любой подобный момент можно считать первым, и это будет своеобразным началом отсчета времени. Здесь можно привести аналогию с началом отсчета времени в календарных системах, поскольку оно тоже здесь условно.
Подводя итог, можно сказать, что движение в космосе полностью определяется шестью числами Ω, i, ω, а, е, τ, которые обычно называют элементами орбиты.
До сих пор обсуждалась идеализированная задача, поскольку предполагалось, что не существует сил, возмущающих описанное движение космического аппарата. На самом деле это не так, возмущающие силы существуют, но они обычно малы. Правда, космические полеты, как правило, достаточно длительны, и поэтому даже малые силы со временем могут приводить к заметным отклонениям от идеального движения по эллипсу. Чтобы избежать сложностей, будем считать, что в каждое мгновение космический аппарат движется по дуге некоторого эллипса, заданного определенными шестью элементами орбиты. Например, если в данное мгновение его движение описывается элементами Ω1, i1, ω1, а1, е1, τ1, то в следующее мгновение – уже элементами Ω2, i2, ω2, а2, е2, τ2, которые могут отличаться от предыдущих.
Такое представление весьма удобно для описания движения, например, искусственного спутника Земли, поскольку возмущающие силы настолько малы и так медленно изменяют орбиту, что движение спутника за время одного своего оборота вокруг Земли почти всегда можно считать происходящим без изменения элементов орбиты. Таким образом, один виток вокруг Земли спутник осуществляет точно по эллипсу, следующий виток, можно сказать, тоже по эллипсу, но с чуточку измененными элементами орбиты и т. д. Следовательно, движение искусственного спутника Земли в целом можно представить как бы склеенным из постепенно изменяющихся эллипсов. Это постепенное изменение и называют эволюцией орбиты космического аппарата.
Рассмотрим два наиболее важных вида эволюции орбиты: торможение спутника атмосферой и прецессию.
Весьма разреженные следы атмосферы, которые находятся на высотах до 1000 км, хотя и очень медленно, но постепенно тормозят движение искусственного спутника Земли. Происходящие при этом изменения формы и размеров орбиты удобнее всего проиллюстрировать, если обратиться к качественному описанию процесса торможения, основываясь на законе сохранения механической энергии (т. е. принять постоянной сумму потенциальной и кинетической энергий). Применительно к космическому аппарату, движущемуся вокруг центрального небесного тела (в нашем случае Земли), этот закон можно записать в такой форме:
| V2 = μ( | 2 | – | 1 | ), |
| r | a |
где V – скорость движения космического аппарата, r – его расстояние от центра небесного тела, а – большая полуось эллипса, по которому происходит движение, и, наконец, μ – некоторая постоянная величина, связанная с массой центрального тела.
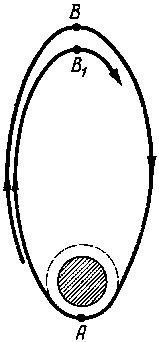 Рис. 3. |
Пусть исходная орбита космического аппарата представляет собой сильно вытянутый эллипс, как показано на рис. 3. Наибольший размер исходной орбиты, т. е. большая ось эллипса (равная, естественно, сумме двух полуосей а, или 2а), дает расстояние между перигеем (точкой А) и апогеем (точкой В, наибольшим удалением от центра Земли, показанной здесь заштрихованной окружностью). Однако в некоторой окрестности перигея траектория космического аппарата погружается в атмосферу, граница которой показана на рис. 3 пунктирной линией. И поэтому здесь движущийся искусственный спутник Земли испытывает определенное торможение атмосферой.
В упрощенном виде этот процесс можно представить себе, как если бы движение спутника в основном происходит вне атмосферы, но в точке перигея на него действует мгновенный тормозящий импульс. Кстати, предположение о мгновенности импульса весьма часто и успешно используется при теоретических исследованиях, если силовое воздействие на спутник кратковременно (по сравнению, например, с периодом обращения). Поэтому говоря даже о маневрировании в космосе, мы всегда будем считать, что включенный ракетный двигатель сообщает космическому аппарату мгновенный импульс, поскольку время работы двигателя обычно измеряется секундами, тогда как период обращения спутника по меньшей мере равен 1,5 ч.
Время пребывания искусственного спутника в области перигея при сильно вытянутой орбите тоже весьма мало по сравнению с периодом обращения. Поэтому и здесь допущение о мгновенности слабого импульса торможения атмосферой вполне законно.
Обратимся теперь к приведенному ранее закону сохранения энергии. Мгновенный тормозящий импульс должен привести к мгновенному уменьшению величины V2, стоящей в левой части равенства. Но тогда мгновенно должна измениться и правая часть (чтобы сохранилось равенство). Величина μ является постоянной, расстояние от центра Земли r тоже останется неизменным, поскольку мгновенный импульс способен изменить скорость, но «не успевает» изменить положение тела, к которому он приложен.
Таким образом, единственная величина, которая мгновенно «реагирует» на изменение величины V2, – размер полуоси эллипса а. Но изменение величины а означает переход спутника на другую эллиптическую траекторию движения. У этой новой траектории перигей останется в точке А, в то время как из-за уменьшения V2 и связанного с этим уменьшения полуоси а точка апогея новой орбиты понизится и окажется в точке В1.
Несколько отвлекаясь от рассмотрения процесса торможения спутника атмосферой, обратим внимание на одно интересное обстоятельство. Мгновенное изменение скорости изменяет орбиту спутника не в той точке, где произошло это изменение: наибольшее отклонение новой орбиты от исходной возникает в противоположной точке эллиптической орбиты. Если бы в точке А включить ракетный двигатель, что практически мгновенно увеличило бы скорость полета, то наибольшее отклонение новой орбиты спутника от исходной снова было бы в апогее, но теперь точка В1 лежала бы выше точки В.
Вернемся к описанию эволюции орбиты искусственного спутника Земли при его торможении атмосферой. Отметим два геометрически очевидных явления – у каждого последующего витка апогей будет располагаться все ниже и ниже (в то время как положение перигея практически не меняется) и одновременно происходит уменьшение эксцентриситета е (уменьшается вытянутость эллипса). В результате уменьшения е и а эллипс постепенно превращается в окружность, причем все меньшего и меньшего размера. В конце концов возникает своего рода спираль, как бы наматывающаяся на земной шар.
Следует отметить, что по мере приближения формы орбиты к окружности высота перигея и высота апогея станут примерно равными величинами и торможение перестанет проявляться как кратковременный импульс, а начнет действовать постоянно. При этом скорость эволюции орбиты увеличится, хотя общий характер такой эволюции орбиты сохранится.
Насколько быстро происходит весь описанный здесь процесс эволюции орбиты?
Однозначного ответа на этот вопрос дать нельзя, все зависит от начальных параметров орбиты. Для пилотируемых искусственных спутников Земли и орбитальных станций время, в течение которого орбита опускается настолько низко, что дальнейшее продолжение полета становится опасным, колеблется от нескольких недель до нескольких месяцев. Продолжение полета оказывается в таких случаях возможным только после выполнения специального маневра (включения ракетного двигателя) в результате которого высота орбиты вновь увеличится.
Другим видом эволюции орбиты, с которым надо всегда считаться, – это так называемая прецессия орбиты, вызываемая несферичностью Земли. Как известно, фигура Земли не является шарообразной, а много ближе к эллипсоиду вращения: расстояние между Северным и Южным полюсами Земли меньше диаметра, измеренного в плоскости экватора. На рис. 4 это показано в сильно утрированном (для наглядности) виде. Прямой ЭЭ обозначена плоскость экватора, прямой NS – ось симметрии Земли, идущая через Северный и Южный полюса.
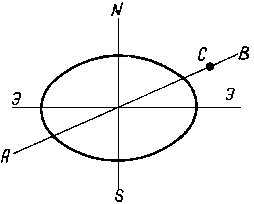 Рис. 4. |
Пусть прямая АВ представляет собой видимую «сбоку» плоскость орбиты искусственного спутника Земли, а точка С – положение самого спутника в рассматриваемый момент времени. Притяжение спутника в точке С частью Земли, лежащей выше плоскости АВ, и частью Земли, лежащей ниже этой плоскости, различно. Ведь лежащая выше плоскости АВ часть Земли в среднем удалена от точки С больше, чем часть Земли, лежащая ниже этой плоскости. Эта асимметрия и приводит к рассматриваемому типу эволюции орбиты.
Под воздействием этой асимметричности ни форма, ни размеры эллиптической орбиты не меняются. Таким образом, элементы орбиты а и е, которые претерпевали существенное изменение в процессе торможения атмосферой, здесь сохраняют свои значения. Но зато в данном случае изменяется положение орбиты в пространстве. Во-первых, изменяется угол Ω (см. рис. 1): плоскость П вращается вокруг оси NS (однако при этом вращении угол между плоскостью орбиты и плоскостью экватора i будет оставаться без изменения). Во-вторых, изменяется положение эллиптической орбиты в плоскости П (см. рис. 2), и поэтому угол ω, как и угол Ω, не остается постоянным.
Таким образом, движение спутника при такой эволюции орбиты происходит по сложной пространственной кривой, которой трудно дать наглядное представление. Эта кривая будет результатом сложения двух вращений – самой орбиты в плоскости П и плоскости П вокруг оси NS. Существенно упрощенную картину можно получить, если учесть малость возмущений, действующих на спутник (ведь показанная на рис. 4 сплюснутость фигуры Земли сильно преувеличена).
Если учесть это обстоятельство, то можно считать, что в течение времени одного витка спутник движется по точному эллипсу, плоскость П неподвижна (угол Ω не меняется) и никакого вращения самой орбиты в плоскости П не происходит (угол ω тоже не меняется). Зато следующий виток должен происходить уже по другой орбите с несколько измененными значениями Ω и ω. В таком представлении фактически непрерывное изменение углов Ω и ω как бы заменяется на ступенчатое, но, поскольку величина этих «ступенек» достаточно мала, такое упрощение вполне допустимо.
Обычно изменение положения плоскости орбиты, определяемое углом Ω, представляет основной практический интерес. Поскольку вращение плоскости орбиты связано с асимметричным характером притяжения спутника частями Земли, лежащими по разные стороны от этой плоскости, то такое вращение отсутствует, если плоскость орбиты АВ на рис. 4 совпадает с плоскостью экватора ЭЭ или проходит через ось симметрии NS. Таким образом, экваториальные (лежащие в плоскости экватора) и полярные (лежащие в плоскости меридиана) орбиты не будут испытывать прецессионного вращения.
Чтобы читатель мог представить себе, насколько существен рассмотренный тип эволюции орбиты, приведем численные данные, характерные для орбит советских пилотируемых космических кораблей, движущихся по орбите искусственного спутника Земли. Для них изменение угла Ω за сутки (за 15 витков) составляет около 4°. Это величина, с которой нельзя не считаться: на экваторе такой поворот дает смещение порядка 400 км.
Однако если торможение спутника атмосферой является практически всегда нежелательным процессом, с которым борются, затрачивая топливо на повторные подъемы высоты орбиты, то прецессионное вращение плоскости орбиты может оказаться иногда полезным. Приведем в этой связи один пример.
Пусть перед астрономическим спутником Земли поставлена задача съемки звездного неба из космоса и пусть он постоянно ориентирован так, чтобы ось телескопа всегда была направлена (относительно центра Земли) точно вверх, в зенит. Как будет показано позже, этого можно достигнуть очень простыми средствами и почти «бесплатно», т. е. почти без затрат топлива или энергии.
Обратимся вновь к рис. 4. За один оборот вокруг Земли наша астрономическая орбитальная обсерватория отснимет звезды, лежащие в узкой полосе (ведь угол зрения телескопов мал), симметричной относительно плоскости орбиты АВ. Если бы не было прецессии орбиты, то орбитальная обсерватория постоянно фотографировала бы одни и те же звезды. Однако при приведенной ранее суточной величине прецессии каждый новый виток будет соответствовать новому положению плоскости АВ и фотографироваться будут все новые звезды. В результате вся доступная для съемки с такого астрономического спутника часть небесной сферы будет отснята за 45 сут без каких-либо затрат топлива на повороты плоскости орбиты (далее будет показано, что такие затраты были бы огромными).
МАНЕВРИРОВАНИЕ В КОСМОСЕ
Маневрирование в космосе, т. е. целенаправленное изменение орбиты, может быть связано как с устранением недопустимых отклонений от заданной траектории полета, возникших вследствие эволюции орбиты, так и с необходимостью перехода на новую орбиту. Начнем изучение проблем, возникающих при маневрировании в космосе, с качественного изучения второй задачи.
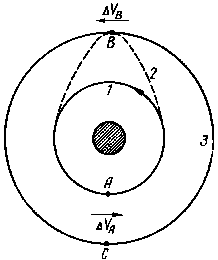 Рис. 5. |
Пусть вокруг Земли (показанной на рис. 5 заштрихованной окружностью) имеются две концентрические круговые орбиты 1 и 3. Задача заключается в том, чтобы спутник, движущийся по орбите 1, перевести на орбиту 3. Это можно сделать следующим образом: в точке А спутнику сообщить дополнительную скорость ΔVА, и в результате он перейдет на новую эллиптическую орбиту 2. Причем наибольшее ее отклонение от исходной (круговой), как уже говорилось в предыдущем разделе, будет в точке В, лежащей в противоположной стороне от точки А.
Если подобрать нужную величину для дополнительной скорости ΔVА, то точка В окажется лежащей на требуемой орбите 3. Тогда в точке В следует осуществить второй разгон спутника на величину скорости ΔVВ, которая требуется, чтобы точка С, противоположная точке В, оказалась на заданном удалении от точки А. Поскольку расстояние точек В и С от центра Земли одинаково, то спутник в результате будет двигаться по заданной круговой орбите 3.
Приведенный пример поучителен в том отношении, что указывает на необходимость нескольких (в данном случае двух) кратковременных включений ракетного двигателя космического аппарата для осуществления некоторого маневра. При этом может оказаться, что между импульсами должно пройти некоторое достаточно большое время. В рассмотренном примере после включения двигателя в точке А надо выждать, пока спутник окажется в точке В. Ведь только из нее (из апогея орбиты 2) можно поднять (удалить от центра Земли) перигей этой орбиты, оказавшийся в точке А.
Причем время движения спутника из А в В будет больше; чем было время перехода спутника из точки А в точку круговой орбиты 1, противолежащую А. Если учесть, что наименьшее время полета по круговой орбите вокруг Земли имеет порядок 1,5 ч, то второй импульс должен последовать за первым не ранее чем через 45 мин.
Можно показать, что изображенный на рис. 5 переход между двумя концентрическими круговыми орбитами по эллипсу 2, касающемуся этих круговых орбит, является энергетически оптимальным. Любой другой переход потребовал бы больших затрат топлива. Этот тип маневра был предложен в 1925 г. В. Гоманом, поэтому эллипс такого перехода и называют иногда эллипсом Гомана.
Если решение задачи об оптимальном двухимпульсном переходе между двумя круговыми орбитами достаточно просто, то проблема оптимального перехода между произвольными орбитами (эллиптическими и лежащими в разных плоскостях) становится значительно более сложной задачей. Она может потребовать и большего числа импульсов, и достаточно сложной стратегии осуществления маневра. В настоящее время теория оптимальных многоимпульсных переходов с одной орбиты на другую представляет собой обширную и интересную область механики космического полета, которая интенсивно разрабатывается и поныне.
Остановимся несколько подробнее на одноимпульсных маневрах, также характерных в практике искусственных спутников Земли. Целью такого маневра является изменение орбиты, т. е. переход от некоторой орбиты, определяемой элементами Ω1, i1, ω1, а1, е1, τ1, к новым элементам Ω2, i2, ω2, а2, е2, τ2. Чтобы упростить рассмотрение задачи, будем считать, что исходная орбита круговая и лежит в плоскости меридиана, причем ограничимся изучением изменений лишь четырех элементов из шести: Ω и i (характеризующие положение плоскости орбиты), а и е (характеризующие форму и размеры орбиты).
Начнем с вопроса о повороте плоскости орбиты. Направление скорости движения искусственного спутника Земли всегда лежит в плоскости орбиты, а поэтому наша задача сводится к повороту направления скорости полета. Чтобы осуществить этот поворот, нужно создать импульс, который должен быть направлен перпендикулярно направлению скорости, т. е. перпендикулярно плоскости орбиты. Рассмотрим два таких маневра: в одном из них изменяется только угол между плоскостью орбиты и плоскостью экватора i, а во втором – только положение восходящего узла на экваторе (угол Ω).
Для осуществления маневра надо развернуть космический аппарат так, чтобы его продольная ось стала перпендикулярной направлению полета, т. е. чтобы он летел «боком вперед», а затем включить на нужное время ракетный двигатель, предназначенный для осуществления маневра. Как уже говорилось во введении, повороты космического аппарата вокруг центра масс не влияют на движение самого центра масс и только включение ракетного двигателя сможет изменить движение центра масс.
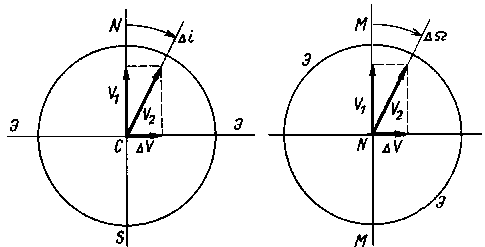 Рис. 6. |
На рис. 6 приведены схемы, поясняющие два типа маневра, поворачивающих плоскость орбиты. На схеме А отражен маневр, приводящий к изменению наклона этой плоскости к плоскости экватора ЭЭ. Пусть исходная орбита будет меридиальной, т. е. ее плоскость содержит прямую NS, соединяющую оба полюса Земли. Тогда прямую NS можно рассматривать как «след» плоскости орбиты на данной схеме.
Если точно над экватором (в точке С) включить ракетный двигатель, то первоначальное движение космического аппарата со скоростью V1 получит дополнительную составляющую ΔV, направленную перпендикулярно направлению скорости V1. Величина ΔV зависит от тяги, развиваемой двигателем, и от длительности его включения. В результате космический аппарат станет двигаться со скоростью V2, имеющей новое направление. Новая плоскость орбиты уже не будет меридиональной, и спутник перестанет периодически появляться над Северным и Южным полюсами Земли. Наклон плоскости орбиты к плоскости экватора изменится на величину, равную Δi.
Схема Б показывает маневр, связанный с изменением положения восходящего узла без изменения угла i. Теперь двигатель надо включать над полюсом, скажем, над Северным полюсом N. Показанная на рис. 6 окружность ЭЭ является линией экватора, прямая ММ дает положение меридиональной плоскости, в которой лежит исходная орбита искусственного спутника Земли. Как и ранее, исходную скорость космического аппарата обозначим через V1, дополнительную скорость, полученную в результате включения ракетного двигателя, – ΔV. Новая скорость V2 будет определять новую плоскость орбиты.
Эта плоскость тоже проходит через точку N, т. е. она, как и исходная, совпадает с плоскостью меридиана, однако теперь другого, отличного от исходного. Новая плоскость орбиты повернута относительно исходной на угол ΔΩ, в то время как наклонение плоскости орбиты к экватору не изменилось. В обоих случаях плоскости орбит совпадают с плоскостями меридианов, т. е. в обоих случаях угол i = 90°.
Если ракетный двигатель включать в других точках орбиты, то будет происходить одновременное изменение как i, так и Ω. Однако более подробное рассмотрение вопроса ничего принципиально нового не даст, поэтому можно ограничиться приведенными примерами. Тем более, что они позволяют сделать главное – оценить «стоимость» поворота плоскости орбиты.
В обоих рассмотренных случаях легко найти углы поворота Δi и ΔΩ. Тангенс этих углов равен ΔV/V1, a следовательно, угол поворота будет равен arctg (ΔV/V1). Пусть, например, необходим поворот на угол 45°. Тогда, поскольку tg 45° = 1, должно быть выполнено условие ΔV = V1. Это говорит о том, что для поворота плоскости орбиты на 45° надо развить дополнительную скорость, равную скорости движения спутника по круговой орбите (для низколетящих спутников она составляет 8 км/с). Но ведь такое может осуществить лишь ракета-носитель, но никак не скромный бортовой двигатель и не при скромных запасах топлива на борту космического аппарата.
Как видно из этого примера, маневр поворота плоскости орбиты – это очень «дорогой» маневр, требующий больших затрат топлива. И его следует всячески избегать. Для этого используются приемы, которых не так уж много. Если необходимо изменить Ω (без изменения i), то иногда можно воспользоваться «бесплатным» прецессионным вращением плоскости орбиты. Если необходимо организовать встречу двух космических аппаратов на орбите, то их старт должен осуществляться так, чтобы получить исходные орбиты с одинаковыми наклонениями i.
Что касается одинаковости углов Ω, то здесь может помочь такой прием. Если космические аппараты стартуют с разных космодромов, то можно воспользоваться тем, что орбита космического аппарата (с точностью до прецессионного вращения) неподвижна в пространстве, в то время как Земля совершает суточное вращение. Достаточно дождаться момента, когда вращающаяся Земля «приведет» второй космодром в плоскость орбиты первого космического аппарата, и лишь тогда осуществить старт.
Бывают случаи, когда избежать большого активного поворота плоскости орбиты нельзя. Например, когда необходимо вывести искусственный спутник Земли на геостационарную орбиту. В этом случае плоскость орбиты совпадает с плоскостью экватора, т. е. угол i равен нулю. В то же время известно, что при старте с некоторого космодрома угол i не может быть меньше широты космодрома. Широта же космодрома Байконур порядка 46°, и, следовательно, поворот на угол, не меньший i = 46°, неизбежен.
Все это говорит о том, что для запуска на геостационарную орбиту необходима дополнительная ступень ракеты-носителя, сам спутник такой маневр выполнить не в состоянии. В этой связи интересно отметить, что запуск геостационарных спутников с территории США представляет собой во много раз более простую задачу: космодром им. Кеннеди (на мысе Канаверал) лежит на широте около 28°.
Повороты плоскости орбиты, осуществляемые за счет бортовых ресурсов собственно космического аппарата, не могут быть очень большими. По порядку величины они не могут превосходить несколько угловых градусов.
Обратимся теперь к осуществлению маневра непосредственно в плоскости орбиты. При повороте плоскости орбиты направление импульса ракетного двигателя было единственным – перпендикулярно плоскости орбиты. Во время маневра в плоскости орбиты направление импульса может быть самым различным: и «вперед», и «вверх», и под некоторым углом к этим направлениям. Если исходная орбита является круговой, то направление «вверх», т. е. от центра Земли, и направление «вперед» будут взаимно перпендикулярными. Поэтому произвольно направленный импульс, создаваемый включением ракетного двигателя, и связанную с ним дополнительную скорость ΔV удобно представить в виде двух составляющих, являющихся проекциями этих величин на направления «вперед» и «вверх». Например, на рис. 7 показаны Земля (дана штриховкой), дополнительная скорость ΔV, сообщаемая спутнику Р, и две составляющие этой скорости в указанных направлениях ΔVT и ΔVS (здесь даны положительные направления составляющих ΔV).
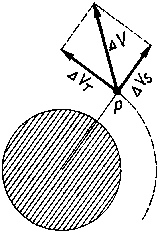 Рис. 7. |
Рассмотрим случай маневрирования в плоскости орбиты, когда VS = 0, т. е. импульс, создаваемый двигателем, направлен параллельно направлению скорости полета (при импульсе, направленном «вперед», осуществляется разгон, а при направленном «назад» – торможение). Как было показано в предыдущем разделе при рассмотрении процесса торможения атмосферой, при этом будут изменяться как большая полуось орбиты а, так и эксцентриситет е. Можно также показать, что соответствующие изменения будут равны:
| Δa = | T | ΔVT | и | Δе = | 2 | |ΔVT|, |
| π | V |
где T – период обращения спутника вокруг Земли, а V – скорость движения спутника по орбите. Во втором выражении стоит абсолютная величина приращения скорости, так как вне зависимости от того, увеличит или уменьшит оно скорость, круговая орбита в обоих случаях станет эллиптической, т. е. увеличится (появится) эксцентриситет.
Обычно основной практический интерес представляют не изменения этих элементов орбиты, а изменение высоты полета, зависящее от обоих элементов. Если мы обратимся к расчету наинизшей (после совершения маневра) высоты полета над Землей, т. е. той высоты перигея, который возникнет в результате маневра, то это изменение высоты Δh может быть вычислено следующим образом:
Δh = Δа – аΔе
(если бы надо было вычислить Δh в апогее, т. е. наивысшую точку орбиты, то было бы Δh = Δа + аΔе). Приведенное выражение свидетельствует о том, что высота полета изменяется как вследствие изменения размеров орбиты (Δа), так и вследствие изменения ее формы (Δе).
Рассмотрение двух слагаемых Δh показывает, что они численно равны друг другу. Действительно, для исходной круговой орбиты полуось а и радиус r совпадают (а = r), а если еще учесть, что период обращения Т = 2πr/V, то отсюда получим равенство Т/π = 2r/V. Обратившись теперь к приведенным ранее выражениям для Δа и Δе, убедимся в справедливости высказанного утверждения.
Если учесть, что для обычных низколетящих спутников Т = 92 мин, V = 7,7 км/с, а расстояние орбиты от центра Земли r = 6800 км (это соответствует исходной высоте полета около 400 км), то получим Δh = –3,5ΔVT [км] при условии, что VT измеряется в метрах на секунду (знак минус означает снижение).
Если опираться на приведенную оценку, то можно утверждать, что тормозящий импульс ΔVT = 100 м/с способен понизить орбиту на 350 км. Поскольку исходная орбита принималась равной 400 км, то это означает погружение искусственного спутника Земли в плотные слои атмосферы, где в результате сильнейшего торможения произойдет снижение спутника до поверхности Земли.
Приведенная оценка (численно она не изменилась бы и при маневре подъема) свидетельствует о том, что маневр в плоскости орбиты сравнительно «дешев». Изменение скорости всего на 100 м/с позволяет увеличивать (при разгоне) или уменьшать (при торможении) высоту полета на несколько сотен километров. Это всегда и делается. В частности, многолетние полеты станций «Салют» на сравнительно низких орбитах (на высотах от 200 до 500 км) возможны только потому, что естественная эволюция орбиты, связанная со слабым торможением в верхних слоях атмосферы, регулярно компенсируется маневрами подъема орбиты путем включения ракетного двигателя. Необходимое для этого топливо доставляют грузовые корабли «Прогресс».
Пожалуй, чаще, чем маневр подъема орбиты, осуществляется маневр уменьшения высоты полета с целью совершения посадки. Об этом уже говорилось чуть ранее, здесь бы хотелось обратить внимание на то, что такой маневр вовсе не обязательно должен быть связан с уменьшением скорости полета, т. е. с торможением. Посадку космического аппарата можно совершить и без изменения скорости его движения по орбите.
Ранее уже обращалось внимание на то, что изменение высоты полета Δh получается и за счет изменения эксцентриситета Δе. Если космическому аппарату придать дополнительную скорость, параллельную вертикальному направлению, т. е. когда от нуля отлична лишь показанная на рис. 7 составляющая ΔVS, a ΔVT = 0, то при обычной малости составляющей ΔVS по сравнению с орбитальной скоростью полета произойдет изменение только направления орбитальной скорости, а не самой этой величины.
В этом случае изменится лишь эксцентриситет Δе = |ΔVS|/V, а Δа = 0. Соответственно получим Δh = –аΔе. Сравнение этой величины с полученной ранее говорит о том, что для изменения наибольшей (или наименьшей) высоты полета Δh потребуется четырехкратное увеличение расхода топлива, чем при таком же изменении при чистом разгоне или торможении. Такая неэффективность затрат топлива делает обсуждаемый маневр нерациональным, и поэтому маневры, связанные с изменением высоты полета (в частности, посадочный маневр), осуществляются за счет составляющей ΔVT, т. е. путем разгона и торможения.
Интересно отметить, что космический корабль «Восток» переходил на траекторию посадки все же не за счет чистого торможения. Чтобы максимально упростить систему управления ориентацией, ось посадочного ракетного двигателя направлялась на Солнце, самый яркий небесный ориентир. Однако в этом случае тяга тормозного двигателя создавала заметную «прижимающую» составляющую, сообщавшую космическому кораблю «Восток» вертикальную составляющую скорости ΔVS .
Надо сказать, что посадить космический аппарат на Землю можно не только чистым «прижатием» (что было бы естественно), но и с помощью импульса, направленного в противоположную сторону – «вверх», в зенит. При этом затраты топлива будут точно такими же, как и при «прижатии». Это, кстати, видно из приводившегося выше выражения для изменения эксцентриситета орбиты Δе = |ΔVS|/V, где знак абсолютной величины у приращения скорости ΔVS означает, что окончательный эффект не зависит от знака ΔVS, т. е. от того, «вверх» или «вниз» направлено это приращение скорости.
Сказанное не означает, конечно, что никакой разницы в новых орбитах не будет. Они, естественно, будут различными, но у них будут одинаковые перигеи (т. е. наименьшие высоты полета над Землей, что только и важно для посадки). При этом в случае «прижатия» перигей окажется очень близко от точки орбиты, в которой сообщается посадочный импульс искусственному спутнику Земли (в 2 раза ближе, чем при импульсе чистого торможения). В то время, как при импульсе, сообщенном «в зенит», перигей будет располагаться в 3 раза дальше, чем в том случае, когда посадочный маневр начинался «прижатием».
В этом смысле посадка, осуществляемая путем сообщения искусственному спутнику Земли импульса, направленного «вверх», представляет собой чисто теоретический интерес. Всякое увеличение времени, требующегося для осуществления посадки, нежелательно. Оно уменьшает точность, а, кроме того, порой возникает необходимость в аварийных посадках, требующих провести срочное приземление.
Рассматриваемый здесь посадочный маневр является только первым этапом при возвращении космического аппарата на Землю, его заатмосферным участком. После входа спускаемого аппарата в плотные слои атмосферы (с высоты порядка 100 км) его движение подчиняется уже законам газовой динамики, а не небесной механики. Огромные силы, возникающие при движении с космической скоростью в плотной атмосфере, вызывают интенсивное торможение. Если спускаемый аппарат не шарообразен, то возможно возникновение и «боковой» силы, перпендикулярной направлению тормозящего импульса.
Направляя эту «боковую» силу «вверх» (для уменьшения скорости снижения спускаемого аппарата), или «вниз» (для более интенсивного «прижатия» траектории движения к Земле), или «вбок» (чтобы скомпенсировать возможную неточность движения в боковом направлении), можно осуществить так называемый управляемый спуск. Именно такой процесс спуска позволяет осуществлять посадку с необходимой высокой точностью.
Здесь полезно отметить, что управление спуском происходит совсем не так, как в авиации. Увеличение или уменьшение скорости снижения осуществляется не путем изменений угла атаки, как у самолета, а путем вращений спускаемого аппарата по крену, причем космонавты могут находиться то в нормальном положении, то вниз головой, то как бы лежа на боку.
Этот необычный способ управления оказался очень эффективным и нашел повсеместное применение, а предложил его еще в 1929 г. Ю. В. Кондратюк. Если управление вести по этой схеме, то сильно облегчается задача теплозащиты спускаемого аппарата, поскольку режим обтекания корпуса движущегося аппарата при поворотах по крену не изменяется.
До сих пор обсуждался процесс спуска космического аппарата на Землю. В известном смысле сказанное справедливо и для спуска на другие планеты, имеющие атмосферу (Марс, Венера). Совершенно иной характер имеет спуск на безатмосферные планеты или, например, на Луну. Здесь гашение скорости может производиться только ракетным двигателем. Та экономия топлива, которая давалась использованием тормозящего действия атмосферы, теперь исключена.
Что касается методики управления посадочным аппаратом, совершающим, например, мягкое прилунение, то здесь используются те же принципы и те же конструктивные решения, что и при подъеме ракеты-носителя. Ведь спуск с использованием тяги ракетных двигателей – это как бы взлет наоборот.
КОРРЕКЦИЯ МЕЖПЛАНЕТНЫХ ТРАЕКТОРИИ. ГРАВИТАЦИОННЫЙ МАНЕВР
Коррекция межпланетных траекторий есть частный вид маневрирования в космосе, но своеобразие этого вида маневра требует специального его рассмотрения.
Прежде всего следует указать на практическую неизбежность таких коррекций. Она может быть проиллюстрирована таким примером. Пусть задачей полета является достижение автоматическим зондом планеты Марс. При старте автоматического зонда необходимо, чтобы он развил скорость, близкую ко второй космической, т. е. 11 км/с. Совершенно естественно, что ракета-носитель не в состоянии развить необходимую скорость абсолютно точно. Пусть неточность получения нужной скорости составляет 1 м/с, т. е. 1/11000 заданной величины (точность порядка 0,01%).
В этом случае промах у Марса будет иметь порядка нескольких десятков тысяч километров. Для посадки же на поверхность Марса требуется точность входа в его атмосферу порядка нескольких десятков километров. Совершенно очевидно, что в рамках поставленной задачи практически нельзя получить нужную точность для выведения межпланетного зонда на трассу перелета Земля – Марс. Разумным выходом из создавшегося положения является вывод межпланетного зонда с технически возможной точностью на орбиту перелета с последующей коррекцией его траектории во время полета.
Сразу после отделения космического аппарата от ракеты-носителя наземный командно-измерительный комплекс начинает проводить измерения, позволяющие определять фактическую траекторию летящего объекта. Эти измерения осуществляются с помощью радиотехнических средств, а результаты измерений сразу поступают в соответствующий вычислительный центр, где и происходит вычисление элементов орбиты. Последние постоянно уточняются по мере поступления новых измерений, и это продолжается вплоть до конца полета.
Поскольку ошибка выведения не может быть значительной, а коррекцию траектории можно провести заблаговременно (т. е. не в непосредственной близости от планеты назначения), то корректирующий импульс будет небольшим. Это позволяет разработать очень простую и наглядную теорию коррекции межпланетных траекторий.
Автоматический зонд движется к планете по эллиптической орбите, в фокусе которой расположено Солнце. Этот характер орбиты нарушается лишь вблизи планеты назначения, поскольку притяжение со стороны близкой планеты дополнительно искривляет траекторию движения. Последнее значительно усложнило бы математическую сторону вопроса, но в теории коррекции межпланетных траекторий обычно анализируют траекторию без учета притяжения планеты назначения. Возникающая в этом случае ошибка компенсируется тем, что планета в такой теории заменяется некоторой условной мишенью. Последняя является плоской и проходящей через центр масс планеты перпендикулярно траектории движения космического аппарата. Причем «яблочко» мишени принимают таким, чтобы условное попадание в него гарантировало бы попадание истинной траектории в планету (с учетом и ее притяжения). Эту «мишень» называют картинной плоскостью.
Пусть теперь маневр коррекции производится на некотором, достаточно большом расстоянии от планеты. Мысленно сообщим космическому аппарату приращение скорости ΔV = 1 м/с во всех возможных направлениях, и тогда каждому направлению будет соответствовать своя точка попадания в картинной плоскости. Одни из этих точек будут ближе, другие дальше от той точки, в которой траектория полета пересекла бы картинную плоскость в отсутствие коррекции. Если соединить плавной линией наибольшие при каждом таком единичном импульсе возможные отклонения, то окажется, что эта граница наибольших возможных отклонении имеет форму эллипса, который называют эллипсом влияния.
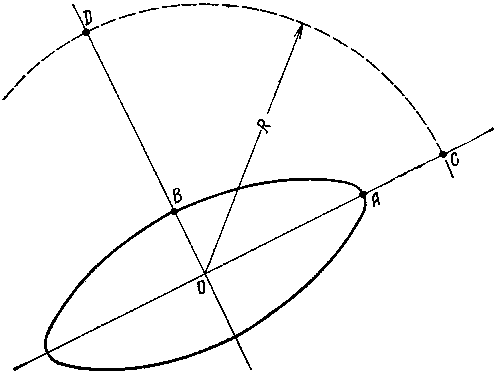 Рис. 8. |
На рис. 8 показан такой эллипс влияния. Точка картинной плоскости О (центр эллипса) соответствует случаю, когда космическому аппарату не сообщалось никаких импульсов. Допустим теперь, что нам необходимо сместить эту точку на расстояние R. Пусть такое смещение проводится в направлении большой оси эллипса, т. е. точка пересечения траектории с картинной плоскостью переносится из О в С. Поскольку отрезок ОС в 1,5 раза больше ОА (получаемого при единичном импульсе), то и нужный нам импульс будет по величине в 1,5 раза больше единичного.
Пусть теперь вместо точки С нам необходимо попасть в точку D. В этом случае, хотя ОС = OD, потребуется импульс уже в 4 раза больше единичного (так как OD = 4OB). Иначе говоря, коррекции, осуществляемые в разных направлениях, неравноценны: одни требуют больше, другие меньше топлива для совершения коррекции.
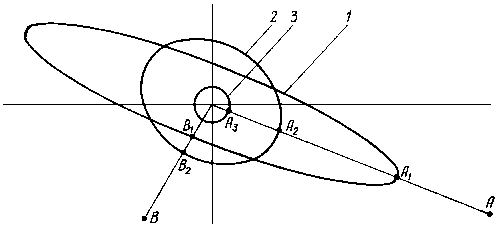 Рис. 9. |
Все эти соображения позволяют пояснить определенную стратегию проведения коррекции. На рис. 9 даны эллипсы влияния для полета к планете Марс, соответствующие времени после старта 1 сут (эллипс 1), 2 мес. (эллипс 2) и 6 мес. (эллипс 3). Рассмотрим случай, когда измерения фактической траектории автоматического зонда показывают, что точку ее пересечения с картинной плоскостью необходимо переместить в точку А. Из рис. 9 следует, что в этом случае коррекцию надо производить как можно раньше, поскольку соответствующие точки на эллипсах влияния (точки А1, А2 и А3) указывают на увеличение необходимого импульса с возрастанием времени полета.
Пусть теперь траекторные измерения показывают, что необходима коррекция, смещающая точку пересечения траектории с картинной плоскостью в точку В. В этом случае вывод будет совершенно иным: с коррекцией не следует спешить, поскольку в первые месяцы после старта величина импульса, необходимого для коррекции, постепенно уменьшается (точка В2 отстоит от центра эллипса дальше, чем В1).
С другой стороны, излишнее затягивание с коррекцией всегда приводит к значительному увеличению расхода топлива. Это также иллюстрируется рис. 9, где эллипс влияния 3 целиком лежит внутри эллипса влияния 2 и значительно меньше последнего.
До сих пор речь шла об импульсах, которые смещают точку пересечения траектории полета с картинной плоскостью. Однако среди всего множества единичных импульсов существует два противоположно направленных импульса, которые не смещают эту точку. И хотя, казалось бы, такая ситуация лишена практического интереса, более внимательное рассмотрение показывает, что это не совсем так. Дело в том, что воздействие приращения скорости ΔV в этом случае хотя и не смещает точку пересечения траектории космического аппарата картинной плоскостью, однако изменяет скорость, с которой автоматический зонд пересекает эту плоскость. При увеличении же скорости (что характерно не только для точки пересечения, но в среднем и для всего участка траектории после коррекции) космический аппарат достигнет цели раньше, чем это произошло бы без такого добавочного импульса. Аналогично можно заключить, что при уменьшении скорости в результате такого импульса встреча с целью будет задержана.
Использование таких корректирующих импульсов становится неизбежным, если возникает необходимость корректировать время встречи с планетой назначения. Ведь планета с определенного пункта (например, с места расположения центра дальней космической связи) наблюдается не круглосуточно. И может оказаться так, что в момент встречи с космическим аппаратом планета уйдет за горизонт в данном пункте. Естественно, такая ситуация обесценит весь эксперимент, и, чтобы это не случилось, надо изменить время встречи. Причем коррекция должна быть такой, чтобы процесс встречи автоматического зонда с планетой мог спокойно прослеживаться из предназначенного для этого пункта.
Конечно, проблемы, связанные с коррекцией межпланетных траекторий, не ограничиваются рассмотренным кругом проблем. Иногда, например, требуется сложная коррекция, в результате которой космическому аппарату сообщается несколько импульсов, разнесенных по времени. В этом случае возникает необходимость в оптимизации такой многократной коррекции. С другой стороны, точность определения фактической траектории растет вместе с увеличением времени траекторных измерений, и поэтому порою приходится задерживать время проведения коррекции (соглашаясь с неизбежным увеличением затрат топлива) или излишне сильно разносить две последовательные коррекции по времени и т. д.
Осуществление маневров в космосе, рассмотренных в предыдущем разделе, и их частных случаев – коррекций траектории полета – связывалось нами с изменением скорости полета космического аппарата по величине или направлению. Для таких изменений нами всякий раз предполагалось включение ракетного двигателя, т. е. требовался определенный расход топлива, запасы которого на борту космического аппарата всегда ограниченны. Возникает естественный вопрос: «Имеется ли возможность осуществлять маневрирование в космосе без затрат топлива?»
Такая возможность в самом деле существует и носит название гравитационного маневра. Последний основан на целенаправленном использовании гравитационных полей небесных тел, около которых пролетает космический аппарат. В этой брошюре мы не будем излагать теорию гравитационного маневра, а ограничимся лишь двумя примерами, иллюстрирующими суть такого способа маневрирования.
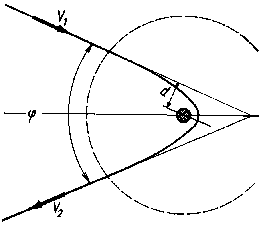 Рис. 10. |
Первоначально рассмотрим маневр поворота направления скорости космического аппарата. На рис. 10 заштрихованным кружком показана планета, а пунктиром вокруг нее – некоторая область, внутри которой действует сила притяжения планеты. Вне этой области гравитационное поле планеты столь слабо, что его действием можно пренебречь.
Космический аппарат приближается к планете со скоростью V1. При попадании в сферу гравитационного влияния планеты (пунктир) траектория его движения под действием притяжения планеты искривляется. В результате космический аппарат станет двигаться по гиперболе с фокусом в центре масс планеты, и после пролета последней он выйдет из этой, как говорят, грависферы со скоростью V2. С учетом закона сохранения энергии V1 = V2, так что эти скорости отличаются лишь своим направлением.
Таким образом, в результате такого маневра изменяется направление полета, причем направление скорости движения повернется на некоторый угол φ. Величина последнего тем больше, чем ближе к планете проходит орбита космического аппарата (т. е. чем меньше расстояние от центра планеты d), которое называют «прицельной дальностью» (оно дает наименьшее расстояние от планеты, если пренебрегать ее притяжением). Проведя путем заблаговременного включения ракетного двигателя сравнительно слабый маневр коррекции, мы можем получить траекторию полета с нужной величиной расстояния d и тем самым вызвать уже сильный эффект, когда направление скорости совершает нужный нам поворот на угол φ.
Каково же предельно наибольшее значение угла φ?
Пусть вся масса планеты практически сосредоточена в центре (естественно, радиус такой планеты равен нулю). Тогда можно получить d = 0, и в этом случае φ = = 180°. Если не рассматривать процессы, протекающие внутри грависферы, а сосредоточить свое внимание на окончательном итоге, то эффект будет точно таким же, как и в случае отскока шарика при упругом соударении с неподвижной преградой или с шаром очень большой массы. В обоих случаях скорости перед входом в грависферу (или перед соударением) и после выхода из грависферы (после «отскока») одинаковы по величине, но направлены в противоположные стороны.
Этот предельный случай позволяет перейти ко второму типу гравитационного маневра. Однако, чтобы сделать следующий шаг в рассмотрении данной проблемы, надо учесть и движение планеты (ведь она не неподвижна, а вращается вокруг Солнца).
Представим теперь, что планета при своем движении догоняет космический аппарат: скорости двух этих объектов направлены одинаково, но скорость планеты больше. Если вновь обратиться к примеру с двумя упругими шарами разной массы, то рассматриваемая ситуация сопоставима со столкновением тяжелого догоняющего шара с более легким. Согласно законам механики легкий шар после удара станет двигаться в том же направлении, что и раньше, но со скоростью, большей скорости тяжелого шара. Легкий шар как бы отскакивает от тяжелого, а тяжелый как бы разгоняет легкий.
Эта наглядная картина поясняет, каким образом гравитационное взаимодействие космического аппарата и планеты способно привести не только к повороту направления скорости, но и к увеличению величины скорости автоматического зонда, к его доразгону. Естественно, полученная космическим аппаратом в результате гравитационного взаимодействия с планетой дополнительная скорость не возникает из «ничего»: при этом уменьшается скорость движения планеты. Однако из-за значительной массы планеты (по сравнению с массой космического аппарата) потерянная ею скорость столь мала, что такой потерей можно и пренебречь.
Следует подчеркнуть, что на самом деле планеты имеют определенные радиусы, и поэтому рассмотренная здесь простая схема взаимодействия никогда не реализуется на практике. Она приведена только в качестве наглядного примера, иллюстрирующего механическую суть и возможности гравитационных маневров.
Современную космонавтику немыслимо представить себе без гравитационных маневров. Впервые такой маневр был на практике осуществлен еще в 1959 г. при реализации эксперимента по фотографированию обратной стороны Луны, который проводился с помощью советской автоматической станции «Луна-3». Во время этого эксперимента возникла следующая проблема (рис. 11, Земля и Луна здесь показаны заштрихованными кругами). Автоматическую станцию первоначально предполагалось вывести на обычную, сильно вытянутую эллиптическую орбиту (обозначенную пунктиром). Поскольку СССР территориально располагается в Северном полушарии, то место старта обозначено на рис. 11 точкой А в этом полушарии. Однако при такой орбите автоматическая станция после фотографирования приблизилась бы к Земле в области В своей траектории, т. е. с юга. В этом случае она не была бы видна с территории Советского Союза.
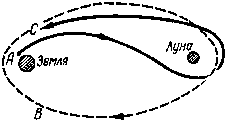 Рис. 11. |
Поэтому был принят другой вариант полета, позволивший при том же старте из точки А возвратиться в результате гравитационного маневра у Луны к Земле с севера (этот вариант указан сплошной линией). Это обеспечило связь с автоматической станцией на подлетном участке С ее траектории. Осуществленные в последние годы полеты автоматических зондов к планетам-гигантам (Юпитер, Сатурн, Уран) были бы невозможны без разгонов и поворотов в результате гравитационных маневров. Гравитационный маневр у Венеры был применен недавно и при полете к комете Галлея советских автоматических зондов «Вега».
В заключение этого раздела полезно остановиться на проблемах, связанных с навигационным обеспечением космических полетов. Задачами навигационного обеспечения являются определение фактической орбиты космического аппарата и прогноз его движения. Совершенно очевидно, что без знания этого маневрирование в космосе невозможно. Обычно такие задачи возлагаются на наземные пункты наблюдения, где для этой цели используются соответствующие радиотехнические средства и наземные вычислительные центры.
Иногда полезно иметь на борту космического аппарата систему автономной навигации, которая в состоянии выполнить навигационное обеспечение самостоятельно, без связи с Землей. Такая система производит необходимые оптические и радиотехнические измерения с помощью бортовых средств и затем обрабатывает полученную информацию с использованием бортовой вычислительной машины.
Здесь хотелось бы подчеркнуть принципиальную разницу между автономной навигацией самолетов и морских судов и автономной космической навигацией. Штурманы морских или воздушных судов в своей работе руководствуются главной целью – определением местонахождения судна в момент наблюдений. Для космического штурмана подобная задача, как правило, лишена смысла. Действительно, если искусственный спутник Земли движется со скоростью 8 км/с, то для него вопрос о точном местонахождении не имеет смысла. Ведь пока командир космического корабля спросит своего навигатора о местонахождении и выслушает ответ, космический корабль будет уже далеко от местонахождения «в момент наблюдения».
Значительно важнее знать траекторию, по которой движется космический аппарат, и, следовательно, «расписание движения» (где и когда он будет в будущем, где и когда он был в прошлом). Для того чтобы иметь возможность говорить об этом, достаточно знать шесть элементов орбиты. Таким образом, задачей автономной космической навигации является не определение своего местоположения в некоторый момент времени, а определение шести элементов орбиты.
Для морских и воздушных судов такая постановка задачи исключена. Ведь морские и воздушные течения делают невозможным точный прогноз движения судна (без вмешательства пилота, рулевого или соответствующих автоматов). Знание (с нужной точностью) траектории неуправляемого движения возможно только в космосе, где полет происходит без возмущающих воздействий внешней среды.
УПРАВЛЕНИЕ ОРИЕНТАЦИЕЙ
Управление ориентацией, т. е. получение нужного положения корпуса космического аппарата относительно некоторых ориентиров (например, звезд), совершенно необходимо для осуществления маневров в космосе. Действительно, ранее всегда предполагалось, что ракетный двигатель сообщает космическому аппарату импульс в нужном направлении: тормозящий (т. е. против направления скорости), «прижимающий», т. е. к центру Земли, в заданном направлении относительно звезд (при коррекции межпланетной траектории) и т. п.
Уже это краткое перечисление показывает, что система управления ориентацией должна содержать приборы, которые позволяют судить о положении корпуса космического аппарата относительно существенных в данной ситуации направлений. В огромном большинстве случаев эту задачу решают с помощью оптических или гироскопических приборов.
Оптические приборы, применяемые в космической технике, весьма разнообразны. Одни из них предназначены для поиска таких ориентиров, как Солнце, яркие звезды (например, Канопус) или планеты. В этих приборах регистрируются обычные видимые световые лучи. Действие других приборов основано на регистрации невидимых инфракрасных лучей (например, специальные приборы, называемые построителями местной вертикали); Дело в том, что при полете искусственных спутников Земли над затененной, ночной стороной Земли обычные оптические приборы становятся неработоспособными, тогда как инфракрасное излучение затененной части Земли мало отличается от инфракрасного излучения ее освещенной стороны.
Разнообразные гироскопические комплексы приборов позволяют измерять угловые скорости вращения корпуса космического аппарата, «запоминать» на некоторое время нужные направления в пространстве и даже выполнять функции, аналогичные тем, которые возлагаются на гироскопические компасы морских судов.
Практика космических полетов выявила наиболее рациональные комбинации приборов, ставшие уже классическими. Так, на искусственных спутниках Земли основную информацию о положении корпуса обычно дают инфракрасный построитель местной вертикали, определяющий направление к центру Земли, и гироскопический прибор (типа гирокомпаса), указывающий на положение плоскости орбиты, т. е. позволяющий судить о направлении «вперед».
При межпланетных перелетах обычно используются оптические приборы, указывающие направления на Солнце и звезду Канопус. Эта звезда выбирается не столько из-за своей яркости, сколько потому, что угол между направлениями на Солнце и на Канопус близок к прямому, а это позволяет получать более точное управление ориентацией. Существуют, конечно, и другие комбинации приборов, удобные для решения тех или иных специфических задач.
Сигналы, полученные с помощью приборов, установленных на борту космического аппарата, поступают затем в бортовую вычислительную машину, которая в соответствии с заложенной в нее логикой вырабатывает сигналы управления. Последние усиливаются и поступают на исполнительные органы системы управления ориентацией, которые и осуществляют повороты корпуса космического аппарата. В настоящее время наиболее распространенными исполнительными органами являются миниатюрные реактивные двигатели (их для краткости часто называют двигателями ориентации) и гиросиловые стабилизаторы.
Двигатели ориентации – это работающие на обычном ракетном топливе маленькие реактивные двигатели. Одной из важных особенностей их работы является их использование в «импульсном режиме», т. е. они способны включаться на доли секунды, чтобы сообщить корпусу космического аппарата минимально возможные вращательные импульсы. Малость размеров таких двигателей и необходимость в импульсном режиме обусловливают то, что они работают с нерегулируемой тягой. В некоторых случаях (особенно для небольших космических аппаратов) вместо ракетного топлива можно применять сжатый газ, истечение которого через сопла двигателей ориентации дает необходимые моменты управления.
Очевидным недостатком двигателей ориентации является то, что для их работы необходимы затраты топлива или сжатого газа, бортовые запасы которых всегда ограничены.
Гиросиловые стабилизаторы – это большие гироскопы, вращение которых обеспечивается с помощью электроэнергии. Последнее является их безусловным преимуществом, поскольку затраты электроэнергии восполнимы в отличие от затрат топлива (например, с помощью солнечных батарей, преобразующих энергию солнечных лучей в электроэнергию). Однако значительная конструктивная сложность и большие массы системы исполнительных органов, содержащей гиросиловые стабилизаторы, делают их использование рациональным лишь в тех случаях, когда велики получаемые от этого выгоды.
Гиросиловые стабилизаторы создают приложенные к корпусу космического аппарата управляющие моменты за счет изменения числа своих оборотов или изменения своего положения в корпусе космического аппарата. Суть первого способа довольно очевидна: если начать раскручивать некоторый маховик в одну сторону, то корпус космического аппарата начнет вращаться в противоположную сторону. Механические явления, связанные с изменением положения оси быстровращающего гироскопа, более сложны, но подобные эффекты вполне нами ощущаются, если мы попытаемся повернуть ось быстровращающегося волчка.
Гиросиловые стабилизаторы успешно используются сегодня на борту метеорологических спутников «Метеор», спутников связи типа «Молния» и на борту некоторых орбитальных станций «Салют».
Поскольку основным типом исполнительных органов систем управления ориентацией являются все же реактивные двигатели, оценим затраты топлива, необходимые для поддержания режима постоянной ориентации. Вопросы же, связанные с переходом из одного ориентированного состояния в другое, мы здесь рассматривать не будем, поскольку идущая на это доля топлива, как правило, мала.
Прежде всего обратимся к тому случаю, когда никаких моментов внешних сил на космический аппарат не действует и ничто не может помешать ему все время «смотреть» на заданный ориентир. В обычных, земных условиях сама постановка подобного вопроса представляется абсурдной. Ведь если ничего не мешает, то зачем затраты топлива?
Чтобы ответить на этот вопрос, обратимся к ситуации, когда необходимо строгое удерживание некоторой оси космического аппарата в направлении на заданный ориентир. Это может быть направлением условной вертикальной оси космического аппарата на центр Земли, или направлением поверхности солнечных батарей на Солнце, или направлением оси телескопа на нужную звезду и т. д. Во всех этих случаях желательно полностью остановить вращение корпуса космического аппарата после того, как относительно ориентира достигнуто нужное положение. Однако в условиях космического пространства это невозможно осуществить. Отсутствие внешней среды, о чем шла речь во введении, приводит к тому, что в космосе сохраняется даже самое слабое вращение, которое в земных условиях было бы сразу остановлено сопротивлением среды.
С другой стороны, невозможно добиться и абсолютной остановки вращения с помощью двигателей ориентации. Как и любое техническое устройство, они работают с известной точностью и после их выключения никогда не наступает полная неподвижность: либо импульса двигателя чуть-чуть для этого не хватает, либо он будет чуточку больше, чем надо. Как бы ни были малы эти скорости, они обязательно «уведут» (пусть через значительный промежуток времени) удерживаемую ось космического аппарата от ориентира.
В зависимости от поставленной цели необходимая точность в удержании некоторой оси космического аппарата в заданном направлении может быть различной, от нескольких угловых минут (при коррекции межпланетных траекторий) до 10 – 15° (при ориентации солнечных батарей на Солнце). Всякий раз, когда малые остаточные угловые скорости, о которых только что шла речь, увеличат угол между ориентиром и ориентируемой осью больше допустимого предела, импульс соответствующего двигателя ориентации «толкнет» корпус космического аппарата в нужную сторону и угол между ориентируемой осью и направлением на ориентир начнет уменьшаться.
Такое движение будет продолжаться и после того, когда этот угол станет равным нулю: пока он снова не достигнет предельно допустимой величины, но теперь уже противоположного знака, движение не прекратится. Чтобы опять вернуть ориентируемую ось в области разрешенных положений, необходимо включить двигатель ориентации, создающий импульс, противоположный первому по своему направлению. В результате возникает вращение (то в одну, то в другую сторону), при котором два двигателя ориентации (вращающие корпус космического аппарата в противоположные стороны), попеременно включаясь, как бы будут бороться друг с другом.
Здесь полезно еще раз подчеркнуть, что эти включения двигателей происходят только из-за отсутствия демпфирующей механическое движение внешней среды в космосе.
Оценим теперь расход топлива двигателями ориентации, необходимый для поддержания таких колебаний. Пусть заданная точность ориентации определяется предельно допустимым углом между ориентируемой осью и направлением на ориентир φ. Тогда размах вращательных колебаний корпуса космического аппарата будет 2φ (от одного предельного значения угла ориентации до противоположного предельного значения этого угла, тоже равного φ).
Будем далее считать, что величина остаточной угловой скорости вращательного движения корпуса ω одинакова при вращениях космического аппарата в обоих взаимно перпендикулярных направлениях. В этом случае период возникших колебаний равен времени вращения в одну, а затем в противоположную стороны. Эти времена t равны друг другу и легко находятся из очевидного равенства t = 2φ/ω, а, следовательно, период колебаний Т равен Т = 2t = 4φ/ω.
За это время каждый из двух двигателей ориентации включится один раз. Это включение каждого двигателя сопровождается расходом некоторой массы топлива, которую обозначим m. Угловая скорость вращения корпуса космического аппарата изменится на величину 2ω: до включения была скорость ω одного знака, а после включения двигателя ориентации стала такой же по величине, но противоположного знака.
Можно показать, что между величинами m и ω существует прямая пропорциональность: 2ω = k1m, где k1 – некоторый постоянный коэффициент. Расход топлива за период колебаний Т (два включения) равен 2m, а средний расход топлива в единицу времени m̃ будет m̃ = 2m/Т, или, подставив значения T и m, получим, что m̃ = ω2/k1φ.
Последнее соотношение, несмотря на свою простоту, имеет принципиальное значение. Оно дает связь между основополагающими характеристиками системы управления ориентацией: расходом топлива в единицу времени m̃, точностью ориентации φ и остаточными угловыми скоростями вращений корпуса космического аппарата ω. Прежде всего следует отметить, что расход топлива обратно пропорционален допустимой точности ориентации. Поэтому систему управления ориентацией никогда не следует делать точнее, чем это на самом деле нужно. Всякое «перевыполнение плана» по точности потребует бессмысленного увеличения нужных бортовых запасов топлива.
На последних еще сильнее сказывается остаточная угловая скорость ω (ее величина входит в полученное ранее соотношение в квадрате). Уменьшение ее в 10 раз дает стократное уменьшение запасов топлива! Неудивительно, что конструкторы систем управления ориентацией стараются сделать эту величину возможно меньшей. В настоящее время она имеет порядок 0,005° в секунду, это медленнее, чем движение часовой стрелки на часах. В этом и заключается причина своеобразия космической техники: при огромных скоростях движения центра масс по орбите, вращения корпуса космического аппарата вокруг центра масс крайне медленны.
ВНЕШНИЕ МОМЕНТЫ
Появление момента внешних сил, или кратко, внешнего момента, действующего на космический аппарат, меняет не только количественную, но и качественную картину расхода топлива на поддержание заданной ориентации. Для упрощения будем считать, что на космический аппарат действует постоянный и большой момент сил. Иначе говоря, из двух двигателей ориентации, которые в рассмотренном ранее случае включались поочередно («толкая» космический аппарат в сторону разрешенных положений корпуса), теперь это делает только один.
Действительно, если внешний момент достаточно энергично поворачивает корпус космического аппарата и под его действием ориентируемая ось подошла к границе разрешенных положений, то для противодействия этому движению должен включиться соответствующий двигатель ориентации. Импульс двигателя ориентации «оттолкнет» космический аппарат от границы, но, если внешний момент достаточно велик, он не даст ориентируемой оси сильно отойти от границы, опять подведет его к ней и все повторится сначала. Противодействующий внешнему моменту двигатель ориентации будет включаться тем чаще, чем больше внешний момент.
Суть механики такого процесса следующая: чтобы нейтрализовать вредное воздействие внешнего момента, двигатель ориентации должен развивать равный ему, но противоположно направленный момент сил. Однако при включении двигатель ориентации создает момент сил, заведомо больший, чем внешний. Это связано с тем, что тяга двигателей ориентации всегда достаточно большая, чтобы они могли не только противодействовать любым внешним воздействиям, но, кроме того, совершать достаточно быстрые повороты корпуса космического аппарата (когда стоит задача не удержания заданного положения, а осуществления поворота из одного положения в другое).
Правда, слова «быстрый» поворот надо понимать с учетом специфики управления в космосе. Эта угловая скорость составляет порядка 1° в секунду, т. е. по земным представлениям будет медленной, однако не надо забывать, что она будет в 200 раз больше угловой скорости колебаний корпуса космического аппарата в процессе удержания его ориентируемой оси в заданном положении. Поскольку развиваемый двигателем ориентации момент сил много больше возмущающего внешнего момента, то двигатель будет включаться импульсно, с заметными перерывами между включениями, но так, чтобы в среднем развить момент, численно равный возмущающему.
Описанная картина противодействия возмущающему внешнему моменту позволяет определить и необходимый для этого запас топлива. Поскольку усредненная величина момента сил, развиваемого двигателем ориентации, численно равна внешнему моменту, действующему на корпус космического аппарата, а расход топлива пропорционален усредненному моменту сил, создаваемому двигателями ориентации, постольку расход массы топлива в единицу времени m̃ в среднем определяется соотношением m̃ = k2Mв, где Мв – численное значение возмущающего внешнего момента, а k2 – некоторый постоянный коэффициент.
Сравнение затрат топлива в единицу времени m̃ для двух рассмотренных случаев показывает совершенно различный характер этих расходов. Когда внешний момент отсутствует, то расход топлива определяется точностью ориентации и угловыми скоростями вращений в процессе ориентации, в то время как при наличии большого внешнего момента – только величиной этого момента. Поэтому первый тип расхода может быть изменен путем настройки системы управления ориентацией, в то время как второй определяется лишь внешними причинами.
Более того, вызванный внешним моментом расход топлива достаточно рационален: он направлен на устранение причин, нарушающих нужную ориентацию. Первый же тип расхода топлива происходит, условно говоря, зря: он не предназначен для борьбы с нарушающими ориентацию причинами, а связан с техническим несовершенством системы управления (невозможность абсолютно точной остановки вращения космического аппарата).
В общем случае, когда на корпус космического аппарата воздействует «средний» момент сил, расход топлива слагается из обеих составляющих. Часть его определяется настройкой системы управления ориентацией, а часть идет на уравновешивание возмущающего внешнего момента. Кроме того, при расчетах нужных запасов топлива следует учитывать, что вращения космического аппарата происходят вокруг трех осей (в авиации сказали бы, что вращения происходят по тангажу, крену и рысканью), т. е. в них принимает участие не два, а шесть двигателей ориентации.
Стремление к экономии запасов топлива (а следовательно, к увеличению продолжительности полета) приводит к тому, что система управления ориентацией включается только тогда, когда это необходимо по существу выполняемых задач. В остальное время она отключена. Это вполне допустимо, так как движение центра масс космического аппарата (движение по орбите) никак не связано с его ориентацией в пространстве (они «развязаны» друг с другом). Таким образом, нарушение ориентации не может «испортить» орбиты (об этом уже говорилось во введении).
Иногда возникает необходимость в длительной, но простой ориентации. Пусть, например, нужно непрерывно удерживать плоскость солнечных батарей перпендикулярно солнечным лучам. Тогда космический аппарат можно сориентировать нужным образом, а перед выключением системы управления ориентацией – придать ему быстрое вращение вокруг оси, направленной на Солнце (превратив космический аппарат в большой волчок). Как известно, быстровращающийся волчок стремится сохранить свое положение в пространстве неизменным, и поэтому солнечные батареи будут еще долго освещаться солнечными лучами, в том числе и после выключения системы управления ориентацией.
Следует лишь добавить, что вращение космического аппарата станет быстрым по космическим представлениям: его угловая скорость всего будет порядка 1° в секунду (один оборот за 6 мин).
Действующий на космический аппарат внешний момент, который существенно сказывается на расходе топлива, вводился ранее формально. Но каковы же причины его появления?
На очень низких орбитах ими могут быть моменты сил аэродинамического происхождения, однако такие внешние моменты не характерны для космической техники. На достаточно больших удалениях от Земли это моменты гравитационных сил (или гравитационные моменты) и моменты сил, связанных с давлением солнечного света. Первые являются основными для высот порядка 300 км от поверхности Земли и выше, а вторые – для межпланетных трасс.
Рассмотрим более подробно случай гравитационных моментов, в значительной степени определяющих облик систем управления ориентацией искусственных спутников Земли. В обычных земных условиях гравитационные моменты неощутимы. Они возникают вследствие двух причин, действующих в одном и том же направлении. Это зависимость силы тяжести от высоты и от того обстоятельства, что эти силы направлены к центру Земли (поэтому в соседних по горизонтали точках они не параллельны). Первая из названных причин дает более весомый вклад в образование гравитационных моментов, поэтому и ограничимся рассмотрением эффектов, которые вызываются только ею.
Прежде всего отметим, что мы никогда не учитываем того, что человек, живущий, скажем; на втором этаже, весит меньше живущего на первом, поскольку более удален от центра Земли (а сила тяжести убывает обратно пропорционально квадрату расстояния до этого центра). Пренебрежение подобным эффектом связано с тем, что разница весов, о которой идет речь, пренебрежимо мала по сравнению с весом человека. Другое дело в космическом полете. Здесь, в условиях невесомости, когда вес тела как бы исчезает, эти малые силы выступают на передний план.
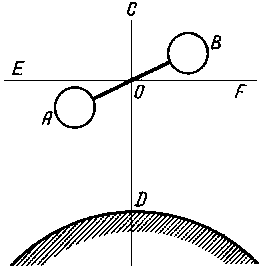 Рис. 12. |
Чтобы нагляднее представить возникающие при этом эффекты, рассмотрим силы, действующие на гантель АВ, находящуюся на орбите искусственного спутника Земли (рис. 12). Поскольку масса А ближе к Земле, чем масса В, первая будет весить больше второй (хотя их массы и одинаковы).
Как известно, свободное твердое тело вращается вокруг центра масс. В рассматриваемом случае центр масс будет находиться в середине гантели (в точке О) и вокруг этого центра будут происходить повороты гантели. Таким образом, точка О является здесь своеобразной «точкой подвеса». Но поскольку масса А весит больше массы В, то масса А стремится, подобно маятнику, занять наинизшее положение, а гантель – стать вертикально, вдоль прямой CD, с массой А, направленной вниз (в сторону Земли).
Если бы удалось привести гантель АВ в такое положение, то никаких сил, выводящих ее из этого состояния равновесия, не существовало бы, как и в случае вертикально висящего маятника. Более того, это положение является положением устойчивого равновесия. Действительно, если отклонить ось гантели от прямой CD, то масса А несколько подымется и будет вновь стремиться привести гантель в вертикальное положение с наинизшим возможным расположением тяжелой массы А.
Вертикальное положение – не единственное состояние равновесия у гантели. Равновесным является и случай, когда направление оси гантели становится горизонтальным, вдоль линии EF. Действительно, в этом случае обе массы (А и В) одинаково удалены от центра Земли, и поэтому их вес тоже одинаков. Нет никакого «стремления» у более тяжелой массы занять в этом случае наинизшее положение, поскольку более тяжелой массы теперь просто не существует. Такое расположение гантели соответствует неустойчивому равновесию: достаточно сколь угодно мало отклонить ось гантели от горизонтали EF, как одна из масс опустится, станет ближе другой к центру Земли (и поэтому тяжелее), и гантель начнет поворачиваться, чтобы ставшая более тяжелой масса заняла наинизшее положение.
Таковы физические причины проявления гравитационных (т. е. связанных с гравитационным полем планеты) моментов, вызывающих вращения твердого тела (а следовательно, и искусственного спутника Земли) в космическом полете. Следует отметить, что не все твердые тела будут вести себя подобным образом. Отправим теперь в космический полет не гантель, а шар. Нижняя половина шара тяжелее верхней, однако поворот шара ничего не изменяет. Если при повороте гантели более тяжелый элемент твердого тела (в наших примерах масса А) имел возможность подыматься или опускаться при поворотах, то у шара этого не будет. Как бы он ни поворачивался, тяжелая часть шара всегда будет оставаться там же, внизу (хотя составляющие ее молекулы твердого тела и будут меняться).
Это «безразличие» шара к поворотам вокруг центра масс и говорит нам о том, что в рассмотренном случае гравитационные моменты не возникают.
Если искусственному спутнику Земли благодаря своему назначению приходится летать в таком положении, когда его продольная ось расположена не по «вертикали» и не по «горизонтали», то на него действует гравитационный момент, воспринимаемый системой управления ориентацией как внешний момент, с которым ей необходимо «бороться».
Поскольку ускорение силы тяжести убывает обратно пропорционально квадрату расстояния от центра Земли и гравитационные моменты уменьшаются по мере удаления от этого центра, то на межпланетных трассах они практически исчезнут. В случае околоземных орбит величина гравитационных моментов зависит от распределения масс в космическом аппарате, и чем ближе оно к шарообразному, тем эти моменты меньше. Кроме того, гравитационные моменты зависят от размеров искусственного спутника Земли. Чем больше космический аппарат, тем они больше, причем с увеличением размеров спутника они растут быстрее, чем возможности противодействовать им. Поэтому по мере увеличения размеров космического аппарата проблема противодействия гравитационным моментам становится все острее.
Всегда ли нужно бороться с гравитационными моментами? Нельзя ли воспользоваться ими для поддержания нужной ориентации?
Ответ на эти вопросы почти очевиден. Если искусственный спутник Земли по причине выполняемой им задачи должен летать в положении, когда его продольная ось все время направлена «по вертикали» (к центру планеты), то гравитационные моменты будут сохранять такое ориентированное состояние. Вспомним пример с гантелью, который показал устойчивость подобного положения равновесия для твердого тела в гравитационном поле Земли.
Это открывает возможность сэкономить топливо космического аппарата, затрачиваемое на поддержание нужной ориентации. Конечно, при других режимах ориентированного полета гравитационные моменты будут помехой, с которой придется бороться, а следовательно, расходовать топливо.
Сегодня целый класс искусственных спутников Земли использует гравитационные моменты для поддержания рассмотренного типа ориентации. О них говорят, что эти спутники используют пассивную систему поддержания нужной ориентации (в отличие от активных систем, требующих затрат топлива и энергии). Обычно они представляют собой сравнительно маленькие искусственные спутники Земли – автоматы, выполняющие какую-либо одну задачу.
Однако использование гравитационных моментов для поддержания нужной ориентации не ограничено только пассивной ориентацией спутников-автоматов. Например, па орбитальных станциях «Салют» тоже существует режим пассивной ориентации, впервые предложенной и осуществленной космонавтом Г. М. Гречко. В этом режиме орбитальная станция постоянно направлена своей продольной осью к центру Земли. Поскольку такой режим полета не связан с затратами топлива, он может быть достаточно продолжительным. Оказалось, что такой вид поддержания ориентации не только весьма экономичен, но и весьма удобен для некоторых научных задач, решаемых на борту орбитальной станции.
При межпланетных перелетах, на далеких от планет участках, где гравитационные моменты становятся исчезающе малыми, на первый план выступают моменты сил, создаваемые давлением солнечного света. В обычной жизни давление света неощутимо, однако на межпланетных трассах с ним необходимо считаться.
Создаваемые им внешние моменты могут тоже использоваться для поддержания нужной ориентации. Так, на советских космических аппаратах «Венера» и «Марс» в длительных режимах ориентации рабочих поверхностей у солнечных батарей на Солнце использовалась довольно сложная (с точки зрения механики) схема ориентации. После того как система управления ориентацией придавала космическому аппарату нужное положение относительно Солнца, корпусу аппарата сообщалось вращение вокруг собственной оси. Дальнейшее его движение вокруг центра масс происходило под действием двух эффектов: эффекта волчка и момента сил, создаваемого давлением солнечного света, причем при действии второго эффекта корпус космического аппарата приобретал свойства обычного флюгера.
Совокупное действие обоих эффектов приводило к тому, что солнечные батареи были все время направлены рабочей стороной на Солнце, отслеживая при этом изменение направления «межпланетный зонд – Солнце» вследствие движения первого по траектории вокруг Солнца.
СБЛИЖЕНИЕ КОСМИЧЕСКИХ АППАРАТОВ
Сближение космических аппаратов и их стыковка являются операциями, без которых немыслима современная космонавтика. Доставка на орбитальную станцию топлива, продуктов питания, научных приборов, запасных частей и, наконец, сменных экипажей или экипажей посещения – все это требует тончайших маневров по сближению транспортных кораблей со станцией. Сближаться можно не только с орбитальной станцией или космическим кораблем, но и с другими объектами, например элементами конструкций, создаваемых в космосе.
Маневрирование при сближении космических аппаратов в известной мере напоминает коррекцию межпланетных траекторий, о которой говорилось раньше. Там тоже требовалось сближение с некоторым небесным телом (планетой) с высокой степенью точности. Принципиальной разницей между этими двумя видами сближений является то, что хотя при сближении с планетой и требуется точный приход в некоторую точку околопланетного пространства (из которой, например, начинается процесс спуска на поверхность планеты), но при этом величина скорости космического аппарата в момент достижения указанной точки практически никакой роли не играет.
Иное дело при сближении с другим космическим объектом, а не планетой. Здесь надо не только подлететь к нему, но и уравнять скорости полета, поскольку иначе при соударении могут быть разбиты оба объекта. Как правило, маневр сближения реализуется в два этапа. Первым является так называемое дальнее сближение – серия маневров (они могут растягиваться на несколько суток), обеспечивающих такое сближение космических аппаратов, что они становятся видны друг другу (слово «видимость» надо понимать шире, чем в обыденной жизни, ею может быть и «радиовидимость», т. е. способность вести взаимное наблюдение с помощью радиосредств). Эти маневры ничем не отличаются от рассмотренных ранее. Их осуществление проводится на «сновании данных наземного командно-измерительного комплекса. Вторым этапом является так называемое автономное сближение, которое осуществляется с помощью бортовых средств, проводящих измерения взаимного положения сближающихся объектов.
Рассмотрим теперь этап автономного сближения более подробно. Для осуществления сближения на этом этапе космические аппараты оборудуются соответствующими средствами для измерения взаимного положения. Обычно такие средства сосредоточены на активном космическом аппарате, который осуществляет маневр сближения, в то время как на пассивном число этих средств значительно меньше или они и вовсе отсутствуют. Так, на активном аппарате устанавливается радиосистема, позволяющая измерять взаимное расстояние сближающихся объектов, скорость сближения и скорость бокового «сноса» (т. е. движения, направленного перпендикулярно прямой, соединяющей сближающиеся объекты). Этих данных оказывается достаточно, чтобы осуществить маневр сближения.
Основываясь на аналогии процесса сближения космического аппарата и с планетой, и с искусственным космическим объектом, можно указать на простейший вид маневра автономного сближения. Сначала сближающемуся аппарату сообщают импульс, обеспечивающий его встречу с назначенным космическим объектом, а в непосредственной близости от последнего сближающемуся аппарату дают импульс выравнивания скоростей (после которого оба объекта будут лететь рядом с одинаковыми скоростями).
Для реализации такого маневра сближения необходимо, чтобы на борту активного аппарата находилась полная информация о собственной орбите, об ориентации космического аппарата относительно Земли, а также бортовая вычислительная машина, позволяющая на основании этих данных и данных о взаимном положении и движении космических аппаратов определить орбиту пассивного объекта и вычислить величины и направления импульсов, реализующих программу сближения.
Как следует из этого краткого перечисления, здесь предполагается наличие сложной аппаратуры на борту активного аппарата. Рассматриваемый метод иногда называют методом свободных траекторий, поскольку сближение здесь происходит по естественной траектории, определяемой законами небесной механики и образующейся после первого (и единственного) импульса сближения, сообщенного космическому аппарату.
Хотя метод свободных траекторий с точки зрения механики является простейшим (один импульс сближения и один импульс выравнивания скоростей) и к тому же энергетически наивыгоднейшим, его недостатком надо считать необходимость использования сложной аппаратуры и бортовой вычислительной машины. Другим методом является метод сближения по линии визирования. Он не требует ни знания своей орбиты, ни знания ориентации космического аппарата относительно Земли, ни бортовой вычислительной машины. В его основе лежит сближение по прямой, соединяющей оба космических аппарата, и для его осуществления достаточно радиотехнической аппаратуры для измерения относительного движения.
Недостаток второго метода сближения – это необходимость сближения по прямой. Дело в том, что полет по прямой линии не является естественным движением в космическом пространстве. В гравитационном поле планеты естественными траекториями будут эллипсы. После каждого импульса, сообщенного активному аппарату, тот сразу переходит на эллиптическую орбиту, которую в силу принятого метода надо будет выпрямлять.
Последнее требует повторных включений ракетного двигателя сближения, причем в направлении, перпендикулярном прямой, по которой происходит сближение. Такие импульсы определят «излишний» расход топлива, ведь они не предназначены для полезных операций (сближения, выравнивания скоростей), а только для выпрямления траектории сближения, поскольку упрощенный состав аппаратуры «не умеет» управлять движением по эллиптическим траекториям.
Если сравнить оба рассмотренных метода сближения с энергетических позиций, то первый из них, не требующий никаких выпрямлений траекторий, будет всегда выгоднее (в смысле затрат топлива), чем второй. Однако потери топлива на выпрямление траектории полета будут тем меньше, чем прямее естественная траектория. Но дуга эллипса тем ближе к прямой линии, чем меньше рассматриваемый его участок, поэтому при сближении на малые расстояния оба метода потребуют почти одинаковых запасов топлива. С расстояний 1 – 2 км оба метода практически одинаково экономичны, а при сближении с расстояний 5 – 10 км и больше метод свободных траекторий становится сначала предпочтительным, а затем – единственно возможным.
Необходимость сообщать сближающемуся космическому аппарату импульсы в разных направлениях при наличии одного ракетного двигателя сближения (он используется и для осуществления маневров в космосе) требует соответствующих поворотов корпуса космического аппарата. Особенно характерно это для сближения по линии визирования. Здесь могут потребоваться импульсы «догона», «выпрямления траектории», «торможения» иногда в довольно сложной последовательности, поскольку из соображений безопасности торможение перед встречей с пассивным объектом осуществляется ступенчато.
Таким образом, процесс сближения есть совокупность чередующихся режимов управления ориентацией и маневров (изменений траекторий полета). Этот своеобразный «танец» активного аппарата не может продолжаться до момента стыковки хотя бы потому, что последний импульс торможения, в непосредственной близости от цели, потребует такой ориентации активного космического аппарата, при которой он будет приближаться к пассивному не стыковочным узлом, а расположенным с противоположной стороны ракетным двигателем. Времени же для переворота может не хватить (вспомним малые угловые скорости вращения при управлении ориентацией!). Поэтому после сближения космических аппаратов на расстояние порядка нескольких сотен метров и выравнивания их скоростей активный аппарат поворачивается стыковочным узлом в сторону пассивного и приступает к операции причаливания.
Операция причаливания проводится так, что в процессе сближения, вплоть до стыковки, ориентация активного аппарата остается неизменной: его стыковочный узел все время направлен в сторону стыковочного узла пассивного. При этом, учитывая, что необходимая точность сближения определяется размерами стыковочного узла, сближение на этапе причаливания должно вестись особенно точно. В процессе причаливания могут потребоваться смещение активного аппарата в ту или иную сторону, уточнение его ориентации на стыковочный узел пассивного, небольшое увеличение или снижение скорости сближения. Последнее необходимо для обеспечения безотказной работы стыковочного узла: слишком большая скорость может привести к поломке, слишком маленькая может оказаться недостаточной для успешного функционирования механических захватов узла.
Чтобы обеспечить все это, на активном космическом аппарате устанавливаются специальные ракетные двигатели причаливания. Они больше двигателей, используемых для управления ориентацией, но много меньше двигателя, предназначенного для маневрирования на орбите и осуществления сближения, предшествующего причаливанию. Число двигателей причаливания велико. Поскольку необходимо иметь возможность смещаться, условно говоря, в направлениях вверх–вниз, влево–вправо, вперед–назад и, кроме того, иметь возможность осуществлять соответствующие повороты (пусть в пределах малых углов), нужна установка двух двигателей по каждому из названных направлений, т. е. всего 12 двигателей. Если учесть, что другие режимы управления (ориентация, маневрирование на орбите) тоже требуют соответствующих двигателей, то общее число ракетных. двигателей, необходимых для полного управления движением, порядка 20.
РУЧНОЕ УПРАВЛЕНИЕ
Ручное управление движением космических аппаратов не является характерным для техники космического полета. Это объясняется разными причинами: тем, что развитие автоматизации – это общая тенденция современной техники, и тем, что космос сначала осваивался автоматами. Сегодня космонавт чаще включает автоматические режимы управления ориентацией или сближением, чем режим ручного управления.
Ручное управление является важным средством дублирования автоматических режимов, а следовательно, средством, существенно увеличивающим надежность всей системы управления. Кроме того, использование ручного управления оказывается более рациональным при осуществлении некоторых научных экспериментов (например, при наведении телескопической установки на нужное созвездие), а также в тех случаях, когда необходимо осуществить управление, не предусмотренное программой полета. Основываясь на приведенных соображениях, все пилотируемые космические корабли или орбитальные станции всегда снабжены и системами ручного управления движением.
Система ручного управления движением, как правило, предназначена для режимов управления ориентацией и причаливания. Другие режимы – автономное сближение, стабилизация положения корпуса космического корабля во время работы двигателя, сообщающего космическому кораблю нужный импульс при маневре, осуществляются соответствующими автоматическими устройствами, а повышение надежности основывается на дублировании этих автоматических устройств такими же или другими автоматами.
Для того чтобы иметь возможность управлять ориентацией или причаливанием космического корабля, космонавт должен иметь достаточно полную информацию о его положении относительно заданных ориентиров (Земли, космического объекта, с которым он сближается, и т. п.). Эта информация носит, как правило, визуальный характер. Космонавт пользуется для этой цели различными оптическими приборами, визирами или телевизионными камерами. Другая необходимая информация выводится на приборную панель, здесь может, например, быть указатель скорости сближения с пассивным космическим объектом. Для упрощения управления при причаливании последний может быть оборудован специальными огнями.
Опираясь на такого рода информацию, космонавт осуществляет управление движением космического корабля путем отклонений специальных ручек управления. Ручка, с помощью которой производится ориентация корабля, имеет три степени подвижности: ее можно отклонять в направлении вперед–назад, влево–вправо и вращать вокруг оси. Каждому из этих трех движений соответствует включение нужных двигателей, они и осуществляют повороты космического корабля вокруг трех осей (по авиационной терминологии, которая имеет здесь лишь условный характер, вокруг осей тангажа, крена и рысканья). Следует заметить, что ручка управления не связана с двигателями непосредственно, а через электронные блоки системы ориентации. Это позволяет улучшить характер управления вращениями космического корабля.
В тех случаях, когда космический корабль предназначен и для стыковки с другим космическим объектом, необходима еще одна ручка, управляющая поступательными смещениями космического корабля. Поступательным движением в механике называется такое, при котором не имеет места вращение, а перемещение центра масс движущегося тела происходит таким образом, что его оси все время остаются параллельными своему начальному положению. Такое движение связано со смещением центра масс корабля, в то время как вращения (изменения ориентации) всегда происходят вокруг центра масс. Очевидно, что в процессе причаливания одинаково важны оба типа движений и вращения, и смещения корабля в направлениях вверх–вниз, влево–вправо и вперед–назад.
Сказанное позволяет утверждать, что космонавт управляет своим кораблем по шести координатам – трем типам смещений и трем видам вращений. Этим управление в космосе принципиально отличается от любого типа управлений, известных в земной практике. И самолет, и морское судно, и автомобиль изменяют движение своего центра масс в связи с поворотами вокруг центра масс. В космосе, как уже говорилось во вводном параграфе, движение центра масс и вращения «развязаны».
Необходимость одновременного управления по шести координатам вызвала в свое время опасения, что космонавт может не справиться со столь сложной задачей. Ведь до этого подобных требований к людям не предъявлялось. Оказалось, однако, что эти опасения были излишними: вероятно, возникшая проблема была существенно упрощена крайне медленным характером взаимных движений космических кораблей в процессе причаливания.
Не следует думать, что режимы автоматического и ручного управления разделены «китайской стеной». Мыслимы случаи, когда космонавт вручную управляет лишь частью движений, поручив управление остальными той части аппаратуры, которая осуществляет автоматическое управление движением.
В принципе ручной контур управления может быть шире, чем описано выше. Не только ориентация и причаливание, но и другие операции могут быть включены в режим ручного управления. Иногда это даже необходимо. Например, при посадке на безатмосферную планету, когда процесс посадки осуществляется, опираясь на тормозящее действие посадочного ракетного двигателя, управление посадкой будет осуществляться автоматически (аппаратурой, во многом похожей на приборы, управляющие взлетом ракеты-носителя). Ведь такая посадка, как уже упоминалось, это своего рода «взлет наоборот». Однако на самом последнем участке спуска, в непосредственной близости от поверхности планеты, необходимо вмешательство космонавта для выбора наиболее подходящей для приземления площадки (лишенной больших камней, оврагов и т. п.).
ЗАКЛЮЧЕНИЕ
Особенности космического полета, связанные с движением в вакууме, о которых говорилось в введении: отсутствие естественного торможения космического аппарата внешней средой, отсутствие случайных возмущений движения (и как следствие возможность точного и длительного прогноза полета космического аппарата) и; наконец, независимость управления движением центра масс космического аппарата, с одной стороны, и вращений аппарата вокруг центра масс, с другой, – все это придает глубокое своеобразие процессам управления в космосе.
Это обусловливает то, что системы управления движением на Земле (в воздухе, на суше, на воде и под водой) и в космосе не просто различаются, а во многих отношениях отличаются принципиально. Внешне это выражается даже в составе приборов управления, устанавливаемых на борту космических аппаратов. Например, оптические датчики в космосе нередко являются основными элементами систем управления, в то время как на Земле в этом качестве они встречаются редко. В космосе широкое распространение получили силовые гироскопы, тогда как на Земле их практически нет.
Надо сказать, что краткий объем брошюры не позволил рассмотреть в ней все вопросы, связанные с управлением движением космических аппаратов. Мы здесь лишь попытались показать необычность проблем, возникающих при разработке методов такого управления. Можно было бы рассказать, например, о проблемах управления, связанных с созданием крупногабаритных орбитальных станций. С увеличением размера космических аппаратов растут и трудности управления их движением. В частности, запасы топлива, необходимые для управления движением орбитальной станции, могут при этом возрасти так, что поднимаемый ею полезный груз станет нулевым по массе. Естественно, такая станция практически не нужна.
Выходом из создавшегося положения может стать вывод неуправляемых станций на орбиту, летающих, например, в режиме пассивной гравитационной ориентации. Такие станции способны стать базой для сравнительно скромных по размерам космических аппаратов различного научного назначения (астрономических, природоресурсных, для изучения физики космоса и т. д.). Благодаря небольшим своим размерам эти космические аппараты смогут легко управляться, а после выполнения требующихся научных задач могут пристыковываться к большой станции для ремонта и регулировки аппаратуры, снятия с них материалов, полученных в экспериментах, и т. д.
Приведенный пример интересен в том отношении, что показывает, как проблемы управления движением определяют не только облик системы управления или даже самого космического аппарата, но решающим образом сказывается на всем составе орбитального комплекса космических аппаратов.
Проблема управления космической системой возникает и тогда, когда по сути выполняемой задачи требуется воспользоваться несколькими космическими аппаратами, находящимися в строго определенных положениях относительно друг друга. Созданная условиями старта конфигурация космических аппаратов со временем постепенно разрушится вследствие малых ошибок выведения и разниц в эволюции орбит. Чтобы это не произошло, т. е. для поддержания заданной конфигурации (своего рода «полета строем»), тоже необходимо соответствующее управление движением.
Перечень задач по управлению движением космических аппаратов можно еще продолжить, но и приведенных примеров достаточно, чтобы стало очевидно воздействие задач управления на облик космических аппаратов как в отдельности, так и входящих в некоторую систему. Это воздействие значительно сильнее, чем в обычной земной практике, где облик корабля или самолета в основном определяется взаимодействием с внешней средой, а запасы топлива – необходимостью преодолевать сопротивления внешней среды.
РЕКОМЕНДУЕМАЯ ЛИТЕРАТУРА
Беляев Н. М., Велик Н. П., Уваров Е. И. Реактивные системы управления космических летательных аппаратов. М., Машиностроение, 1979.
Елисеев А. С. Техника космических полетов. М., Машиностроение, 1983.
Кубасов В. Н., Данков Г. Ю., Яблонько Ю. П. Методы сближения на орбите. М., Машиностроение, 1985.
Левантовский В. И. Механика космического полета в элементарном изложении. М., Наука, 1980.
Раушенбах Б. В., Токарь Е. Н. Управление ориентацией космических аппаратов. М., Наука, 1974.
ХРОНИКА КОСМОНАВТИКИ*
* ПРОДОЛЖЕНИЕ (см. № 12 за 1985 г.) По материалам различных информационных агентств приводятся данные о запусках некоторых искусственных спутников Земли (ИСЗ) и полетах автоматических межпланетных станций (АМС), начиная с ноября 1985 г. О пилотируемых космических полетах рассказывается в отдельных приложениях. О запусках ИСЗ серии «Космос» регулярно сообщается, например, на страницах журнала «Природа», куда и отсылаем интересующихся читателей.
1985 г.
15 НОЯБРЯ в СССР запущен очередной (17-й) ИСЗ связи «Радуга». Выведенный на стационарную орбиту к точке «стояния» .35° в. д., он получил международный регистрационный индекс «Стационар-2». Наряду со стационарными ИСЗ типа «Горизонт» и «Экран», а также ИСЗ типа «Молния-1» и «Молния-3» эти ИСЗ широко применяются в системах телевизионного вещания, действующих в нашей стране.
27 НОЯБРЯ с борта МТКК на стационарную орбиту к точке «стояния» 116,5° з. д. выведен 2-й мексиканский ИСЗ «Морелос», предназначенный для национальной спутниковой системы связи (ССС). Он полностью аналогичен 1-му ИСЗ «Морелос», запущенному 17 июня 1985 г. (более подробно об этой ССС см. в приложении к № 11 за 1985 г.).
28 НОЯБРЯ с борта МТКК на стационарную орбиту к точке «стояния» 164° в. д. выведен 2-й австралийский ИСЗ «Авссат», предназначенный для национальной ССС Австралии. Он полностью аналогичен 1-му ИСЗ «Авссат», запущенному с борта МТКК 27 августа 1985 г. Запуск 3-го ИСЗ «Авссат» планируется провести с помощью западноевропейской ракеты-носителя (РН) «Ариан» (более подробно об этой ССС см. в приложении к № 11 за 1985 г.).
29 НОЯБРЯ с борта МТКК на стационарную орбиту к точке «стояния» 77° з. д. выведен 1-й ИСЗ «Сатком К» нового поколения национальной гражданской ССС американской корпорации РКА. Всего предполагается изготовить 4 ИСЗ «Сатком К», которые оснащены ретрансляторами диапазона К (14/12 ГГц), в отличие от ИСЗ «Сатком», работающих в диапазоне 6/4 ГГц (более подробно об этой ССС см. в приложении к № 11 за 1985 г.).
24 ДЕКАБРЯ В СССР на высокоэллиптическую орбиту с высотой апогея 40 793 км в Северном полушарии выведен очередной (27-й) ИСЗ связи «Молния-3». Как и ИСЗ связи типа «Молния-1», эти ИСЗ являются составными элементами ССС, используемой для дальней телефонно-телеграфной радиосвязи и передачи телевизионных программ в системе «Орбита».
25 ДЕКАБРЯ в СССР с помощью одной РН на круговые орбиты высотой 19 160 км одновременно запущены ИСЗ «Космос-1710», «Космос-1711» и «Космос-1712», предназначенные для отработки элементов и аппаратуры космической навигационной системы, создаваемой в целях обеспечения определения местоположения самолетов гражданской авиации и судов морского и рыболовного флотов Советского Союза.
26 ДЕКАБРЯ в СССР на круговую орбиту высотой около 950 км запущен очередной (13-й) советский оперативный метеорологический ИСЗ «Метеор-2». Выводимые на околополярные орбиты, эти ИСЗ обеспечивают получение глобальных изображений облачности и подстилающей поверхности в видимом и инфракрасном диапазонах, а также наблюдения за потоком проникающих излучений в околоземном пространстве. Аппаратура ИСЗ «Метеор-2» может работать как в режиме запоминания, так и в режиме непосредственной передачи информации, поступающей в Государственный научно-исследовательский центр изучения природных ресурсов и в Гидрометеоцентр СССР Госкомгидромета.
1986 г.
12 ЯНВАРЯ с борта МТКК на стационарную орбиту к точке «стояния» 67° з. д. запущен 2-й ИСЗ «Сатком К» для американской ССС корпорации РКА.
17 ЯНВАРЯ в СССР на стационарную орбиту к точке «стояния» 25° в. д. (международный регистрационный индекс «Стационар-8») запущен очередной (18-й) ИСЗ связи «Радуга».
24 ЯНВАРЯ американская АМС «Вояжер-2» совершила пролет около планеты Уран на расстоянии 81 000 км от вершины ее облачного покрова. В результате исследований окрестностей Урана открыто несколько новых спутников планеты, получены интересные сведения о самой планете. После гравитационного маневра АМС «Вояжер-2» перешла на траекторию полета к планете Нептун, около которой АМС пролетит в 1989 г.
28 ЯНВАРЯ в США трагически закончился запуск МТКК Челленджер» (см. «Хронику пилотируемых полетов»), при помощи которого предполагалось, в частности, вывести на орбиту ИСЗ «ТДРС» и «Спартан-Галлей». С выводом на стационарную орбиту 2-го ИСЗ «ТДРС» (1-й был запущен с помощью МТКК 4 апреля 1983 г.) должно было завершиться создание государственной ССС ТДРСС, предназначенной для слежения и ретрансляции данных от американских ИСЗ (в том числе и МТКК) на низких орбитах (более подробно об этой ССС см. в приложении № 11 за 1985 г.). Создание ССС ТДРСС было приурочено к началу эксплуатации орбитального блока «Спейслэб» в 1983 г., однако потребовавшаяся доработка космического буксира «ИУС», обеспечивающего вывод ИСЗ на стационарную орбиту, а также устранение неисправностей в системах 2-го ИСЗ «ТДРС», обнаружившихся при предстартовых испытаниях, сильно задержали окончательное формирование данной ССС и привели к существенному сокращению программ исследований во время полетов блока «Спейслэб». В ходе полета МТКК планировалось также вывести на автономную орбиту ИСЗ «Спартан-Галлей» (с возвращением на Землю на борту МТКК), оборудованный двумя ультрафиолетовыми спектрометрами, предназначенными, в частности, для исследований кометы Галлея. Тщательное расследование причин катастрофы на мысе Канаверал, а также необходимые работы по обеспечению надежности МТКК потребуют определенного времени. Это может значительно отодвинуть сроки запусков американских ИСЗ и АМС, выводимых в космос с помощью МТКК. В частности, на многие месяцы сейчас отложены запуски АМС «Галилей» к Юпитеру и АМС «Улисс» к полюсам Солнца, планировавшиеся на май 1986 г. Кроме того, возможная доработка МТКК должна привести к существенному удорожанию программы «Спейс Шаттл», не говоря уже о том, что потеря МТКК «Челленджер» не только не позволит теперь возместить стоимость его изготовления (1,2 млрд. долл.) при многоразовом использовании, но, видимо, потребует незапланированных затрат на изготовление еще одного МТКК.
Хроника пилотируемых полетов 1
| № | Дата | Космонавты (первым указан командир КК)2 | КК3 | Продолжительность полета | ||
| сут | ч | мин | ||||
| 113 | 27.XI 1985 | Б. Шоу (2) Б. О'Коннор (р. 1946) Д. Росс (р. 1948) М. Клив (р. 1947)4 Ш. Спринг (р. 1944) Ч. Уолкер (3) Все США Р. Нери (р. 1952) Мексика | А | 6 | 21 | 04 |
| 114 | 12.I 1986 | Р. Гибсон (2) Ч. Болден (р. 1946) Ф. Чанг-Диас (р. 1950) Дж. Нельсон (2) С. Хаули (2) Р. Сенкер5 Б. Нельсон (р. 1943)6 Все США | К | 6 | 02 | 04 |
| 1157 | 28.I | Ф. Скоби (2) Д. Резник (2)4 М. Смит (1945 – 86) Э. Онизука (2) Р. Макнайр (2) Г. Джарвис (1945 – 86)8 Ш. Маколифф (1949 – 86)9 Все США | Ч | |||
1 ПРОДОЛЖЕНИЕ (см. № 12 за 1985 г.).
2 Выделены космонавты, впервые стартовавшие в космос (у остальных в скобках указано число полетов в космос).
3 Для космических кораблей (КК) приняты обозначения: А – «Атлантис», К – «Колумбия», Ч – «Челленджер».
4 Женщина-космонавт США.
5 Представитель корпорации РКА.
6 Председатель подкомиссии конгресса по космическим исследованиям.
7 Через 1 мин после старта произошел взрыв американского КК, конструкция которого не предусматривает, в отличие от советских КК, применение системы аварийного спасения (все космонавты погибли).
8 Представитель фирмы «Хьюз».
9 Учительница средней школы.
НОВОСТИ АСТРОНОМИИ
КАКОВ УРАН ВБЛИЗИ
Первые же результаты, полученные во время пролета АМС «Вояжер-2» около планеты Уран, оказались весьма неожиданными. В первую очередь это касалось магнитного поля планеты, существование которого предполагалось по аналогии с Юпитером и Сатурном, обладающими достаточно мощными магнитосферами. Правда, Уран хотя и является тоже планетой-гигантом, однако существенно уступает в размерах этим планетам. Кроме того, Уран движется по орбите вокруг Солнца, «лежа на боку», т. е. ось собственного вращения планеты находится почти в плоскости орбиты Урана. Поэтому время от времени эта планета обращена к Солнцу (и к Земле) непосредственно одним из своих полюсов – случай совершенно уникальный по сравнению с другими планетами Солнечной системы. В настоящее время Уран повернут к Солнцу своим южным полюсом. Оба эти обстоятельства – меньшие размеры и необычность обращения вокруг Солнца – заставили некоторых ученых даже усомниться в том, что у Урана есть магнитное поле. Тем не менее оно было обнаружено, да к тому же его интенсивность в радиационных поясах оказалась выше, чем в случае Сатурна (что стало полной неожиданностью).
Облачный покров Урана имеет в целом голубовато-зеленоватый цвет. Однако над южным полюсом обнаружилось обширное темное пятно, так что при подлете АМС к планете та казалась гигантским глазом со зрачком в виде темного пятна над южным полюсом. Самое удивительное, что температура атмосферы над южным полюсом планеты, освещаемым Солнцем, оказалась существенно ниже температуры атмосферы над северным полюсом, находящимся в тени уже в течение нескольких лет. Облака в атмосфере Урана движутся на различных широтах с разными скоростями, обнаружены атмосферные вихри, а также струйные течения со скоростью 100 м/с в направлении вращения планеты. По коротковолновому радиоизлучению планеты период вращения Урана около своей оси предварительно определен как 16 ч 18 ± 18 мин.
Многих, естественно, интересовали кольца, обнаруженные недавно вокруг Урана с Земли. При помощи телекамер АМС были получены изображения всех девяти известных колец, а также еще одного нового кольца, причем по предварительным оценкам размеры частиц в самом внешнем кольце оказались достаточно внушительными – от 1 до 10 – 15 м (значительно превышающими размеры частиц колец Сатурна, а тем более Юпитера). Вся система колец Урана покрыта плотным облаком пыли; частота соударений АМС с пылевыми частицами достигала 30 в секунду. Помимо колец, было обнаружено около 10 образований в виде дуг длиной 50 – 60 км. Не исключено, что выявлены сегменты еще одних колец, но слишком темных, а потому и не обнаружимых целиком с помощью телекамер АМС.
В ходе своего пролета около Урана АМС совершила пролет и около всех пяти известных его спутников. Интересно, что чем ближе спутник находится к планете, тем более деформированной оказалась его поверхность. На Обероне сравнительно мало следов эрозии поверхности, на Титании – их несколько больше. На Умбриэле очень много кратеров, и он темнее остальных спутников (предполагают, что у него самая древняя поверхностная порода по сравнению с остальными спутниками). На Ариэле обнаружено массивное растрескивание поверхности и следы ее деформированного растяжения. А на сравнительно небольшой (поперечником около 500 км) Миранде выявлено несколько сотен кратеров, крутые каньоны с изрезанными краями, гладкие овальные и «взрыхленные» прямоугольные образования, пирамиды из дискообразных глыб, высочайшие (до 24 км) горы и очень глубокие (до 16 км) долины. Некоторые элементы рельефа Миранды указывают на возможность сейсмической активности. Наконец, кроме известных больших спутников АМС обнаружила с десяток малых спутников размером от 15 до 150 км. Количество этих спутников, видимо, возрастет при продолжающемся сейчас анализе снимков, полученных с помощью АМС. В частности, ученые предполагают обнаружить так называемые «спутники-пастухи» около каждого из колец Урана, подобно аналогичным спутникам около колец Сатурна. Пока открыты два таких спутника размером 15 и 19 км, располагающиеся по разную сторону от самого внешнего из колец Урана.
В настоящее время полученные результаты продолжают обрабатываться и анализироваться, и изложенные здесь сведения, несомненно, будут дополнены и уточнены.
Associated Press, 1986, 24 – 27 января
Борис Викторович Раушенбах
УПРАВЛЕНИЕ ДВИЖЕНИЕМ КОСМИЧЕСКИХ АППАРАТОВ
Гл. отраслевой редактор Л. А. Ерлыкин
Редактор Е. Ю. Ермаков
Мл. редактор Л. Л. Нестеренко
Обложка художника А. А. Астрецова
Худож. редактор Т. С. Егорова
Техн. редактор Н. В. Лбова
Корректор И. Н. Тереховская
ИБ № 7754
Сдано в набор 19.12.85. Подписано к печати 12.02.86. Т 05379. Формат бумаги 84×1081/32. Бумага тип. № 3. Гарнитура литературная. Печать высокая. Усл. печ. л. 3,36. Усл. кр.-отт. 3,57. Уч.-изд. л. 3,53. Тираж 30 570 экз. Заказ 2782. Цена 11 коп. Издательство «Знание». 101835, ГСП, Москва, Центр, проезд Серова, д. 4. Индекс заказа 864203.
Типография Всесоюзного общества «Знание». Москва, Центр, Новая пл., д. 3/4.

4-я стр. обложки
