"Техника-молодежи" 1953 г, №2, с. 31-35

Жидкостные ракеты, применяемые сейчас в разных странах, построены по схеме, впервые предложенной К. Э. Циолковским. По опубликованным данным, они поднимаются на высоту 200 с лишним километров. Составные жидкостные ракеты достигают еще более высокого «потолка» — поднимаются на 400 км. В этих конструкциях ракете до ее запуска сообщается первоначальный разгон с помощью другой ракеты. Когда нижний двигатель отработал, он автоматически отцепляется и опускается на парашюте. В работу вступает второй двигатель.

400 км высоты — много ли это?

По сравнению с расстояниями до небесных тел — это, конечно, очень немного. Даже спутник Земли — Луна — находится от нас почти в тысячу раз дальше.

Но все-таки, и с точки зрения межпланетных полетов, 400 км — это высота весьма значительная.

Необходимо учитывать одно обстоятельство: сила притяжения Земли, как и всех других небесных тел, быстро уменьшается по мере удаления от ее центра. Она ослабевает так же быстро, как освещенность предметов по мере их удаления от источников света. Это обстоятельство в значительной степени облегчает задачу межпланетных путешествий.

Подъем груза на высоту 2 м требует в 2 раза большей работы, чем подъем его на 1 м. Но для того чтобы поднять груз на миллиард метров, вовсе не требуется совершать в миллиард раз большую работу. На самом деле здесь получается огромная экономия — энергии потребуется в полтораста раз меньше предполагаемой величины.

Величину работы, которую нужно совершить для того, чтобы вырваться за сферу земного притяжения, можно представить себе из такого примера: энергия, затрачиваемая на поднятие груза в 6,4 т на 1 м над поверхностью Земли, равна энергии, нужной для того, чтобы выбросить камешек весом в 1 г в мировое пространство.

Обозначим работу, необходимую для удаления данного тела с поверхности Земли в бесконечность, единицей (эта работа, отнесенная к единице массы, представляет собой потенциал Земли). Какую долю данной работы необходимо затратить, чтобы поднять или подбросить это же тело на определенную высоту?

Математический анализ показывает, что эта величина равна максимальной высоте, до которой дойдет или будет поднято данное тело, деленной на его максимальное расстояние от центра Земли (высота плюс радиус Земли). Чтобы поднять тело на высоту в десять радиусов Земли, потребуется ⁹/₁₀ этой энергии, а в сто радиусов — ⁹⁹/₁₀₀. Пользуясь этим законом, мы можем установить, какую долю работы, необходимой для удаления в бесконечность пустой ракеты, выполнили двигатели, поднявшие ее до 400 км. Округляя величину радиуса Земли до 6 400 км, мы получаем 400: (400+6 400)= 1:17. Это, конечно, очень много.

Изменение величины силы тяжести по мере удаления от центра планеты. Толщина спирали изображает величину силы тяжести в любой точке, расположенной на ее внутреннем крае. Круги с радиусом, кратным радиусу планеты, служат для глазомерной оценки расстояний от центра.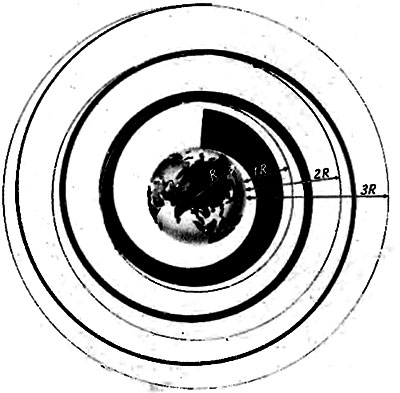

Если же принять во внимание, что для превращения тела в искусственный спутник требуется половина энергии, необходимой для удаления его в бесконечность, то получится, что современные ракеты, если можно так выразиться, с точки зрения развиваемой энергии, уже на ¹/₉ космические. В связи с этим не будет лишенным интереса вспомнить, что еще пятнадцать лет назад жидкостные ракеты не поднимались на высоту десяти километров.

Во сколько же раз придется увеличить скорость современной ракеты для превращения ее в искусственный спутник Земли?

С точки зрения развиваемой скорости, современные ракеты уже более чем на ⅓ космические.

Правда, ракета, поднимающаяся на 400 км, достигает максимальной скорости в 2 250 м в сек. Искусственный же спутник, вращающийся тут же за пределами атмосферы, должен обладать скоростью, более чем в 3 раза превышающей эту величину. Но это вопрос не простой арифметики. Следует еще учесть работу, затраченную на подъем ракеты, на преодоление сопротивления воздуха и гравитационные потери во время взлета. (Эти последние потери выражаются в том, что при работающем двигателе приращение скорости ракеты в поле тяготения меньше, чем вне его.) Однако при соответствующем выборе траектории и режима работы двигателя эти потери небольшие.

Таким образом, «идеальную скорость», то-есть скорость, которой могла бы достигнуть современная ракета в свободном пространстве¹, пришлось бы увеличить всего примерно в 3 раза. С помощью составных ракет эта задача может быть решена уже в наши дни. Наука сегодня находится накануне осуществления космического полета.

¹ Под этим названием подразумевается пространство, лишенное сопротивляющейся среды и удаленное от небесных тел на достаточное расстояние, чтобы можно было пренебречь силами тяготения. Схема гипотетического перелета Москва—Караганда за четверть часа на испытательной космической ракете. При посадке ракета тормозит свою скорость с помощью своих двигателей. Налево сверху показано, как сила тяжести уменьшает ускорение движения корабля. Наверху направо — общий вид земного шара и траектория полета ракеты.

Чтобы легче было заглянуть в ближайшее будущее космонавтики, познакомимся с еще одним благоприятным для осуществления межпланетных полетов фактором.

При отлете с земной поверхности последующее увеличение «потолка» на одинаковую величину требует все меньшего и меньшего прироста скорости. Поэтому надо полагать, что рекорды высот на вертикально взлетающих ракетах будут достигаться скачкообразно, пока, наконец, не наступит день, когда взлетевшая ракета не покинет навсегда нашу планету.

Многие считают, что космическая ракета должна обязательно быть снабженной двигателем, работающим на ядерном горючем. Такое мнение ничем не оправдано.

Современные ракеты, работающие на термохимическом (обычном) топливе, имеют скорость истечения газов до 2 500 м в сек. Можно предполагать, что скоро удастся довести эту скорость до 4 тыс. м в сек.

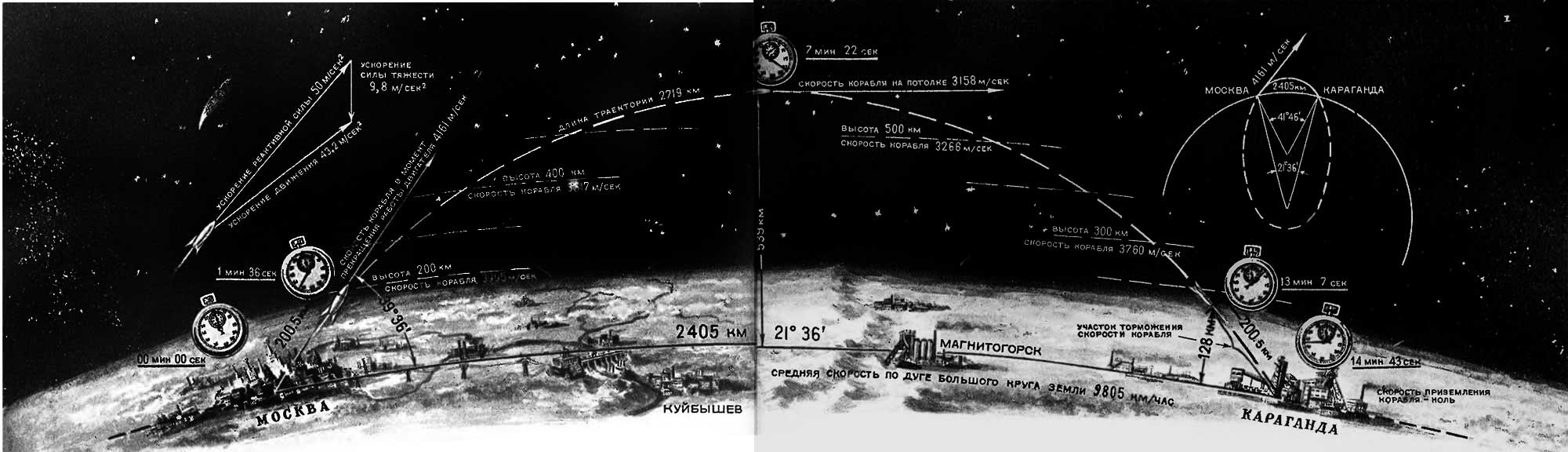Схема гипотетического перелета Москва-Караганда за четверть часа на испытательной космической ракете. При посадке ракета тормозит свою скорость с помощью своих двигателей. Налево сверху показано, как сила тяжести уменьшает ускорение движения корабля. Наверху направо — общий вид земного шара и траектория полета ракеты.

При такой скорости истечения газов и достаточно большом относительном запасе топлива космический полет вполне осуществим.

В настоящее время вес уносимого жидкостной ракетой топлива превышает в 3 и более раза вес самой ракеты. И здесь в связи с применением все более качественных материалов и более удачных конструкций можно надеяться на дальнейшие успехи.

Нельзя, однако, забывать, что ракету с данным двигателем нельзя чересчур загружать топливом, иначе она может вовсе не подняться. И вообще сильно перегруженный двигатель не способен сообщить ракете большую скорость.

Это не значит, что конструкторы не стремятся, например, в баки поместить как можно больше горючего и окислителя, но одновременно с этим они увеличивают мощность двигателя. Ибо чем больше тяга ракетного двигателя, тем при прочих равных условиях меньше топлива уходит для достижения данной цели.

Итак, в современном ракетостроении наблюдаются тенденции к увеличению скорости истечения газов, относительного запаса топлива, мощности двигателя, количества составных ступеней ракеты.

Достигнутые на всех этих участках успехи подведут нас вплотную к созданию космической ракеты.

Самой простой по конструкции является ракета с постоянной тягой. В такой ракете секундный расход топлива, а также режим работы насосов и других механизмов не меняются за все время полета. Обычно ракеты на жидком топливе строятся именно такого типа. Однако такая ракета с не очень большой скоростью истечения газов не может быть использована для межпланетных путешествий, если даже предположить, что она способна взять с собой необходимое количество топлива для достижения необходимой скорости.

По мере расхода топлива масса ракеты постепенно уменьшается, а так как действующая тяга ракеты остается постоянной, то приращение скорости корабля в каждую последующую секунду — ускорение ракеты — будет постепенно увеличиваться. Одновременно с этим увеличиваются и силы инерции внутри ракеты.

Положим, что во взлетающей вертикально ракете ощутимое ускорение равно ускорению силы тяжести на уровне моря. На пружинных весах в ней подвешена однокилограммовая гиря. Когда по мере сгорания топлива вес ракеты уменьшится вдвое, стрелка весов перейдет на цифру 2. Когда же останется лишь одна треть первоначальной массы ракеты, стрелка будет показывать 3 кг. Находящиеся на ракете люди ощущали бы тогда утроенный вес собственного тела. При скорости истечения газов, равной 3 км в сек., ракета на высоте в 416 км достигла бы параболической скорости, если бы отсутствовало сопротивление воздуха. В этот момент вес тела на ракете увеличился бы в 100 раз. Такого увеличения веса не в состоянии выдержать не только человек, но и ракета, — корпус ее разлетелся бы на мелкие части.

В жидкостных ракетах в конце так называемого активного участка, то-есть в конце полета со включенным двигателем, ощутимая тяжесть увеличивается в 7 — 11 раз против существующей на поверхности Земли.

Однако есть возможность использовать ракеты с постоянной тягой для достижения космических скоростей, избежав больших ускорений. Для этого ракета должна быть ступенчатой и каждая последующая ступень должна иметь менее мощный двигатель, в соответствии с уменьшенной массой ракеты. В этом случае в конце периода работы каждого двигателя сила инерции не будет чрезмерно возрастать.

Существует также возможность использования для космического полета простой ракеты с постоянной тягой путем значительного увеличения скорости истечения газов из сопла. Чем больше эта скорость, тем меньше необходимый запас топлива. А когда в ракете меньше топлива, ее конечная масса не будет существенно отличаться от начальной и тем самым разница в весе находящихся на ракете тел в начале и в конце работы двигателя будет менее ощутимой. Если скорость истечения газов из взлетающей вертикально космической ракеты увеличить с 3 до 5 км в сек., тогда вес тел на ракете увеличится лишь только в 19 раз. При использовании ядерного горючего с очень большой скоростью истечения газов прирост веса будет совсем незначительным.

Наиболее подходящей для совершения космического полета ракетой нужно считать ту, в которой ощущение тяжести постоянно. В таком аппарате по мере выгорания топлива секундный расход истекающих газов должен постоянно уменьшаться. Это обеспечит телам, находящимся на его борту, неизменность веса. В такой ракете время работы двигателя и высота горения не ограничены. При вертикальном взлете на ракете описываемого типа параболическая скорость достигается на высоте меньшей или в крайнем, теоретическом, случае равной радиусу Земли. При последнем условии ощущаемая на борту ракетного корабля тяжесть равна тяжести на поверхности Земли.

При вертикальном взлете на ракете описываемого типа параболическая скорость достигается на высоте меньшей или в крайнем, теоретическом, случае равной радиусу Земли. При последнем условии ощущаемая на борту ракетного корабля тяжесть равна тяжести на поверхности Земли.

Положение, в котором находится летчик во время взлета, имеет существенное значение для конструкцией ракеты. Чем удобнее положение летчика, тем большее ускорение он может перенести. А чем больше ускорение, на которое рассчитана ракета, тем меньше топлива требуется ей для достижения одной и той же цели.

Нормально переносимое летчиком ускорение составляет 40-50 м в сек².

В лежачем положении летчик сможет выдержать секундное приращение скорости в 100 м в сек.

Применение кушетки специальной формы делает летчика, как показали опыты, еще более выносливым к ускорению, особенно если он будет лежать вниз лицом.

В лабораторных условиях на своеобразных «каруселях» люди уже неоднократно, без вреда для здоровья, подвергались центробежному ускорению, равному и даже превышающему ускорение на будущих космических пакетах и даже в течение более длительного времени чем это потребуется при взлете в мировое пространство.

Законы природы благоприятствуют развитию космонавтики: при незначительном увеличении скорости космического корабля его «потолок» значительно поднимается.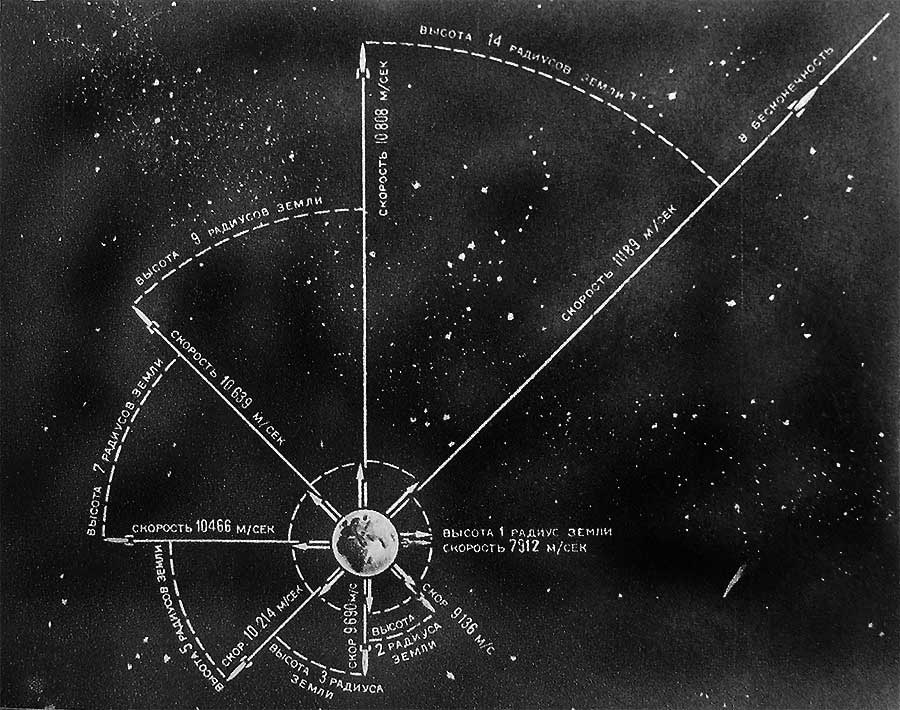 Картинка из недалекого будущего: первые советские космонавты вступили на покры­тую толстым слоем вековой пыли почву Луны...

Мы, правда, не имеем доказательств, что отсутствие силы тяжести, возникающее на ракете после выключения двигателя, будет безвредно для человека. Но, в худшем случае, можно, как предлагал К. Э. Циолковский, заменить силу тяжести центробежной силой.

Несмотря на то, что ракеты с постоянной тягой способны достичь каких угодно больших скоростей, они имеют ограниченное время горения и при вертикальном взлете ограниченный, сравнительно низкий «потолок». Например, при скорости истечения газов в 3 км в сек. максимальная высота полета с включенным двигателем не может превысить 459 км при продолжительности его работы в 306 сек.

Ракета «Фау-2», имеющая скорость истечения газов 2 135 м в сек., не могла бы при любых технических усовершенствованиях (увеличение количества горючего и окислителя при одновременном уменьшении веса конструкции и упразднении полезного груза, уменьшении аэродинамического сопротивления и т. д.) работать при вертикальном взлете дольше 3 мин. 37 сек. (практически двигатель «Фау-2» работает около 70 сек.). Такая ракета не могла бы также при любых обстоятельствах работать на высоте свыше 225 км.

На первый взгляд такое явление кажется парадоксальным, но оно легко объяснимо. При постоянной тяге секундный расход топлива остается постоянным. Следовательно, спустя строго определенное время баки должны опорожниться. Достигнутая же к этому времени высота, таким образом, также ограничена.

Высказанные здесь положения представляют не только теоретический интерес: они имеют большое практическое значение. Они показывают, например, что при стендовых испытаниях не стоит сверхмерно увеличивать время горения двигателя. Заметим кстати, что одной из труднейших проблем ракетостроения является именно создание камеры сгорания с соплом, выдерживающим высокие температуры и давления, правда в течение очень короткого периода времени.

Как показывает математический анализ, максимальные высота и время горения описанной выше ракеты зависят исключительно от ускорения силы тяжести на поверхности планеты, в данном случае Земли, и от скорости истечения газов. Только изменение этой скорости влияет на максимальные время и высоту горения, которые растут, соответственно, пропорционально скорости истечения газов и ее квадрату.

Иногда приходится слышать удивленный вопрос: «Почему невозможно вырваться из сферы земного притяжения при скорости менее 11 км в сек.? Ведь с помощью ракетного двигателя не трудно подниматься на сколько угодно?»

Чтобы ответить на этот вопрос, нужно установить: возможен ли космический полет при постоянной скорости, характерной для современных самолетов?

Вертикально взлетающая ракета сохранит постоянную скорость, сообщенную ей у поверхности Земли, если компенсировать ускорение земного тяготения. Как известно, это ускорение с высотой убывает.

Для достижения очень далеких от нашей областей вселенной космический корабль не должен все время двигаться с первоначальной скоростью. На определенном расстоянии от Земли можно выключить двигатель и продолжать удаляться по инерции. Правда, скорость корабля, начиная с этого момента, будет беспрерывно, хотя и медленно, снижаться, но все же корабль уже никогда не остановится и не упадет обратно на Землю.

Каков же будет общий расход топлива для выполнения нашей задачи при скорости взлета, например, в 850 км в час? Это зависит от скорости истечения газов из ракеты. Допустим, что эта скорость равна 4 км в сек. и что вес ракеты не превышает 1 т. Тогда для достижения нашей цели понадобилась бы масса топлива большая, чем вся масса Земли.

Увеличение скорости полета очень резко уменьшит необходимое количество топлива.

Почему же при больших ускорениях требуется меньше топлива? Сила земного притяжения уменьшает тягу ракеты, но эта убыль менее чувствительна для ракеты, летящей с большим ускорением.

Положим, есть две ракеты, движущиеся в пустоте, в малом, практически неощутимом поле тяготения. Одна летит с ускорением в 15 м/сек², а вторая — с вдвое большим. Спустя 2 сек. с момента начала движения первая ракета будет обладать скоростью в 30 м/сек, вторая же ракета достигает такой же скорости еще в конце первой секунды.

Пусть теперь наши ракеты взлетают вертикально с поверхности Земли. Сила притяжения нашей планеты уменьшит их ускорение примерно на 10 м/сек². Спустя 2 сек. первая ракета будет обладать скоростью (15 м/сек²-10 м/сек²) X 2 сек. = 10 м/сек, а вторая по истечении 1 сек. будет двигаться со скоростью (30 м/сек²— 10 м/сек²) X 1 сек. = 20 м/сек. Как видно, гравитационные потери, возникшие вследствие помещения ракеты в поле тяготения, сказались меньше на ракете с большим ускорением — ей понадобится меньше топлива для достижения определенной скорости.

Первым космическим кораблем станет ракета, способная превратиться в искусственный спутник Земли.

Какую же «идеальную скорость» должна для этого развить ракета?

Допустим, что искусственному спутнику предназначено вращаться на высоте 300 км. Соответствующая круговая скорость составляет 7732 м в сек. Требуется также выполнить некоторую работу, чтобы поднять ракету на такую высоту и преодолеть сопротивление воздушной оболочки Земли. Имеются еще гравитационные потери, потери на исправление траектории вследствие возможных неточностей в работе механизмов и приборов, а также вследствие незначительного, не постоянно действующего сопротивления воздуха на орбите искусственного спутника.

Принимая во внимание все эти обстоятельства, мы приходим к заключению, что ракета должна развить идеальную скорость в 9 640 м в сек.

Но как испытать такую ракету в летных условиях?

Для этого мы можем сначала сообщить ракете половину идеальной скорости (9 640 : 2 = 4 820 м в сек.), а затем с помощью ее же двигателей затормозить эту скорость. Это даст нам возможность убедиться, что ракета будет способна развить необходимую скорость для превращения ее в искусственный спутник Земли. Можно также направить нашу ракету с обладаемой ею скоростью в полет по соответственно подобранной траектории в пределах Земли.

Как показывают расчеты, она может покрыть 2 405 км, то-есть, например, расстояние Москва — Караганда, за 14 мин. 43 сек. (см. рис. на 32, 33 стр.).

Ракета взлетает в Москве с ускорением реактивной силы (ощутимое ускорение) в 50 м/сек². Но вследствие геометрического сложения силы притяжения Земли и тяги ракеты ускорение ее движения составляет лишь 43.2 м/сек². Спустя 96,4 сек. на высоте 127,8 км, когда ракета пролетит 200,5 км, ее двигатель прекращает работу. В это мгновение ракета обладает скоростью 4 161 м в сек. (в свободном пространстве ее скорость составляла бы 4 819 м в сек.) Начиная с этого момента, она летит по инерции по дуге эллипса, характеристики которого показаны на рисунке.

После того как ракета перейдет через «потолок», ее скорость опять начинает возрастать, достигнув на высоте 127,8 км. 4 161 м в сек.

В этот момент начинается торможение с помощью ракетных двигателей. Оно длится 96,4 сек. — столько же, сколько период взлета. За четверть часа ракета покроет расстояние Москва — Караганда.

И настанет другой день, когда летчик опять сядет за штурвал корабля, аналогичного по конструкции нашей ракете. На сей раз он не будет больше тормозить скорость аппарата, а станет постепенно ее увеличивать. И когда двигатели, с перерывами, отработают свои 193 сек., ракета уже не упадет больше на Землю. Превратившись в небесное тело, она будет кружить вокруг нее.

Наша страна — родина реактивной техники. Придет час, когда первые советские стратопланы устремятся исследовать космическое пространство.