Е.Зенгер К механике фотонных ракет 1958 г. в djvu 2,27 Мб скачать

Книга содержит основы механики ракет, приводимых в движение реакцией потока фотонов, выбрасываемых из ракеты. По мнению автора, фотонные ракеты позволят совершать полеты в самые отдаленные области Галактики.

Книга рассчитана на научных работников и инженеров, занимающихся вопросами реактивной техники и космических полетов.

Космические путешествия и связанная с ними возможность встречи с разумными существами в других мирах - все это давно волнует людей. Однако до последнего времени весь круг вопросов, относящихся к таким путешествиям, был лишь темой научно-фантастической литературы.

Научно-техническая революция, происшедшая за последнее десятилетие и приведшая к бурному развитию атомной энергетики и ракетной техники, позволила перенести вопрос о космических путешествиях из области научной фантастики в область реального. В настоящее время, после запуска советских спутников Земли, вряд ли кто-нибудь может сомневаться в осуществимости космических полетов. Реализация таких полетов под силу людям. Однако на этом пути стоит немало научных и технических трудностей, поскольку проблема космических полетов является намного более сложной, чем все проблемы, с которыми человечество встречалось до сих пор.

Простые оценки позволяют заключить, что колоссальное расстояние, которое необходимо преодолеть в космическом полете за время жизни одного поколения, потребует, чтобы такой полет совершался с максимальной возможной скоростью, близкой к скорости света. Таким образом, здесь техника уже не может исходить из классической механики, она вынуждена базироваться на законах релятивистской механики (теории относительности).

Простые энергетические соображения позволяют также заключить, что для приведения в движение космической ракеты следует использовать реактивное действие фотонов (световых квантов), обладающих равной нулю массой покоя. Механике ракет, использующих реактивное действие фотонов, и посвящена книга известного немецкого ученого и инженера Зенгера «К механике фотонных ракет».

Автор не обсуждает технических аспектов фотонной ракеты. Источники энергии и конкретные механизмы превращения масс покоя в излучение также не рассматриваются. Автор подробно рассмотрел лишь одну из проблем - механику полета релятивистской фотонной ракеты. Такое рассмотрение может быть проведено в настоящее время до конца на основе механики теории относительности.

Релятивистские эффекты - сокращение масштабов, отставание движущихся часов - приводят к весьма своеобразным свойствам полета фотонной ракеты¹). Так, благодаря релятивистскому сокращению длин принципиально возможна такая ситуация, при которой пассажиры ракеты, проведя в полете несколько лет своей жизни, возвратятся на Землю через несколько десятилетий (по земным часам) и вместо современников застанут на Земле лишь своих потомков. Естественно, что такой «полет к потомкам» потребует решения колоссальных технических проблем, однако принципиально он возможен. Автор рассматривает подобную возможность, причем в расчетах фигурируют лишь ускорения порядка величины земного ускорения²). Книга Зенгера является первым полным исследованием, в котором на базе теории относительности рассматривается механика полета космических ракет. Она, несомненно, даст толчок к дальнейшим исследованиям в этой области.

Книгу прочтут с интересом ученые и инженеры, работающие в области ракетной техники.

И. М. Халатников.

1) Автор иногда употребляет выражение «сверхсветовая скорость», понимая под этим скорость, вычисленную по расстояниям, измеренным неподвижным наблюдателем (например, земным), и по промежуткам времени, измеренным по часам на движущейся ракете. Определенная таким образом скорость, естественно, может превышать скорость света.

2) Благодаря тому что движущиеся часы всегда отстают, противоречащий принципу причинности «полет в прошлое», естественно, неэозможен.

Искусство высокоэффективного превращения массы покоя в энергию движения делает быстрые успехи, и поэтому кажется оправданным изучать применение этого превращения в реактивном приводе. Настоящее введение в механику фотонно-реактивного привода представляет собой первую часть обширной программы научных работ в области фотонно-реактивных приводов, за которой должны последовать дальнейшие работы по физике горения, физике излучения, отражению излучения и поглощению излучения в фотонно-реактивных двигателях.

В настоящей работе сделана попытка дать основы возможно более общей релятивистской механики реактивного привода, в которой механика фотонно-реактивных приводов содержится лишь как важнейший частный случай, в то время как все другие примеры приводов средств передвижения, такие, как химические и ядернохимические ракетные приводы, прямоточные реактивные, турбо-реактивные и пропеллерно-реактивные приводы вплоть до приводов водных и наземных экипажей и биологических приводов, представляют собой другие частные случаи.

Количественная оценка важнейшего частного случая фотонно-реактивного привода позволяет сделать следующее заключение: полеты в столь далекие области Галактики, что возникает конечная вероятность встречи с неземными разумными существами, скорее всего могут быть осуществлены при техническом сочетании принципа фотонно-ракетного привода с принципом прямоточной фотонной ракеты.

Однако и для межпланетных полетов и полетов в атмосфере фотонно-реактивные приводы обещают дать окончательное решение проблемы привода.

Настоящая работа, в частности, приводит к следующему существеннейшему выводу: если вместо теплотворной способности горючей смеси ввести коэффициент превращения массы покоя в энергию ε и использовать парциальность π процесса выталкивания горючего и внутренний коэффициент полезного действия η_i, характеризующий полезную передачу энергии направленной струе масс горючего, то получаемый на единицу массы горючего импульс можно представить как функцию скорости света с в самом общем случае в виде

Таким образом, функциональная зависимость этого импульса от расхода энергии выражается не параболой, как это обычно принимается, а, строго говоря, окружностью.

Хотя в частном случае фотонной ракеты скорость выталкивания всегда равна с, однако удельный импульс может, в зависимости от величин ε, η_i, π, принимать любое значение вплоть до верхнего граничного значения 30571 сектон/кг для полной фотонной ракеты при полном превращении масс в излучение; это более чем в сто тысяч раз превышает обычный удельный импульс современной химической ракеты.

Можно ожидать, что скорости полета фотонных ракет будут более высокими, чем скорости современных ракет, в том же отношении, т. е. что они могут превзойти скорость света.

При столь высоких скоростях полета мир ракеты и ее экипажа будет иметь очень малое отношение к миру их старта, и относительные различия кинематики полета и динамики привода для системы отсчета, связанной с местом старта, и для собственной системы отсчета экипажа ракеты окажутся очень большими.

Поэтому экипаж в своем уединенном мире полета будет пользоваться собственным счетом времени, он будет безотносительно к внешнему миру измерять свое собственное время t_e и свое собственное ускорение Ь_е с помощью обычно применяемых для этого приборов, находящихся на борту, и путем механической интеграции этих двух измерений сможет найти по законам классической механики собственную скорость v_e, которая может сделаться сколь угодно большей, чем скорость света, и собственный путь s_e, совершенно отличный от того, который измеряют астрономы Земли, но определяющий, однако, расход горючего в двигателе ракеты. Вскоре после превышения скорости света экипаж установит, что в галактическом пространстве сопротивление межзвездного газа полету ракеты достигает значительной величины и в короткое время полностью прекращает дальнейшее увеличение скорости ракеты только за счет работы ракетного двигателя. В этом случае экипаж может принимать в ракету натекающие межзвездные массы по способу прямоточного реактивного двигателя, использовать их в качестве топлива и с высокой скоростью выталкивать обратно. Таким способом можно в большой степени уменьшить сопротивление полету в межзвездной среде, однако производить при помощи него заметные положительные ускорения по принципу прямоточного реактивного привода невозможно, так как разность между скоростями принимаемой и выталкиваемой масс стремится к нулю.

Таким образом, фактический расход горючего может быть покрыт полностью из запаса масс, имеющегося на борту ракеты (принцип чистого ракетного привода), или же может быть пополнен в дороге посредством приема масс из окружающей среды (принцип прямоточного реактивного привода).

Последний принцип не годится, конечно, как сказано выше, для ускорения ракеты; при помощи его можно только устранить сопротивление межзвездного пространства и благодаря этому сохранить без применения ракетного привода имеющуюся скорость полета или сделать возможным дальнейшее ускорение при помощи ракетного привода, как в свободном от сопротивления пространстве.

Так как скорость встречи межзвездного газа с ракетой представляет собой величину порядка скорости частиц первичного космического излучения, то, с одной стороны, создаются благоприятные предпосылки для проведения далеко идущих ядерно-химических реакций превращения вещества в излучение и, с другой стороны, оказывается, что качество современных строительных материалов еще не достигло уровня, который соответствовал бы современным представлениям о действии этого ветра полета на граничные поверхности. Постоянные собственные ускорения, которые целесообразно применять в таких межзвездных полетах, по порядку величины совпадают с земным ускорением и поэтому не вызывают никаких физиологических затруднений.

Применением простого ускорения, равного земному, скорость света может быть достигнута через собственное время в 3·10⁷ сек., или 0,95 года, при уменьшении первоначальной массы ракеты m*_e2 вследствие расхода горючего в отношении m_e2/m*_e2 = е^-1 = 0,368. Десятикратная скорость света может быть достигнута, следовательно, спустя 9,5 года при отношении масс m_e2/m*_e2 = е^-10= 10^-4,24.

Если бы экипаж при столь высоких собственных скоростях вел наблюдения окружающего мирового пространства, то он нашел бы космос, в соответствии со своей собственной скоростью, в значительной мере уменьшенным и искаженным как в пространстве, так и во времени, так что более не существовало бы возможности ориентировки на основе имеющихся собственных измерений.

Чтобы установить связь с метрикой мирового пространства, определенной земными астрономами, экипаж должен связать результаты своих собственных измерений с соответствующими величинами, полученными земным наблюдателем.

Такая связь, например, между значениями одного и того же элемента времени, когда он измеряется земным наблюдателем (dt) и экипажем (dt_e), имеет вид dt/dt_e = ch (v_e/c); следовательно, при собственном эйнштейновом числе полета v_e/c = 10 дилатация времени между земным наблюдателем и экипажем составляет уже dt/dt_e = 0,5 е¹⁰ = 10^3,94, т. е. экипаж живет почти в десять тысяч раз медленнее, чем земной наблюдатель. Собственное время экипажа начинает течь все более и более медленно, и экипаж начинает приближаться к безвременному состоянию, которое должно быть приписано жителям фотона.

Соответствующая связь между скоростью v относительно Земли и собственной скоростью v_e ракеты есть v/c = th (v_e/c). Как ни велика будет собственная скорость ракеты, ее относительная скорость, конечно, никогда не достигнет скорости света.

Важнейшая связь существует между относительным расстоянием s земных астрономов и измеряемым в ракете собственным путем s_e; в общей форме эта связь имеет вид ds/ds_e = (sh v_e/c)(v_e/c) и, например, для постоянного собственного ускорения ракеты

Таким образом, как только v_e/c станет заметно больше единицы, астрономическое расстояние s, определяющее коэффициент полезного действия рейса, возрастет в огромной степени по сравнению с собственным путем s_e, определяющим расход горючего, так что в течение немногих лет жизни экипажа и при конечном расходе горючего может быть пройдено любое астрономическое расстояние. Для воображаемых жителей фотона наш внешний мир сократился бы до размеров нуля, так как их собственная скорость бесконечно велика.

Самые большие собственные скорости v_e, необходимые для путешествия вокруг Вселенной, достигают примерно 25-кратной скорости света подобно тому как для движения вокруг Земли по инерции необходима 25-кратная скорость звука.

Время, необходимое для этого путешествия, составляет при применении просто ускорения силы тяжести примерно 42 года и может быть снижено применением постоянного трехкратного земного ускорения примерно до 15 лет, причем, однако, полный расход горючего несколько повышается.

В противоположность этим неожиданным связям кинематических собственных и относительных величин соответствующие связи динамических величин менее сенсационны.

Величина сопротивления пространства, производимого соприкасающимися с ракетой массами пространства, зависит, конечно, от скорости полета относительно этих масс, но не зависит от системы отсчета наблюдателя, следовательно, она одинакова для экипажа и для земного наблюдателя.

Напротив, величина ускорения ракеты, производимого выталкиваемыми массами, не зависит непосредственно ни от скорости полета, ни от системы отсчета наблюдателя.

Как с уединенной высоты последней горной вершины видим мы бесконечную новую страну, лежащую перед нами, и наука и техника вселяют в нас уверенность, что от нас самих, от людей, будет зависеть, овладеть ли этой страной или же пренебречь ею. Но пренебрегали ли мы когда-либо обетованной землей?

Неисчислимые миллиарды часов человеческого труда, затраченные в мире за последние десятилетия на обеспечение национальной безопасности, могли бы превратить землю в райский сад. Иногда можно прийти в отчаяние при мысли о том, что этого не удалось достигнуть из-за раздоров между дипломатами и государственными деятелями, которых, пожалуй, можно было бы избежать. Или, быть может, великая суровая природа этими болезненными средствами должна достичь какой-то хорошей цели, которая нами, людьми, остается неосознанной?

Мы, люди воздушных полетов, уже давно имеем маленькое утешение в том, что эти миллиарды часов человеческого труда помогали нам также натягивать над землею все более плотную сеть воздушных сообщений, все более надежных и более быстрых.

Мы, люди воздушных полетов, радуемся тому, что радар и ядерная энергия уже вносят или скоро внесут в это свою долю, что турбо-реактивные двигатели удваивают скорости наших путешествий, а прямоточные реактивные двигатели, может быть, скоро сблизят для путешественников континенты на часовые расстояния.

Мы, люди полетов в пространстве, гордимся тем, что уже посылаем наши ракетные зонды до крайних слоев атмосферы и что многие науки извлекают из этого пользу.

Теперь в том же направлении появились две новые и важные проблемы, решение которых стало возможным в результате последних успехов в развитии оружия дальнего действия; это - строительство над землею «внешних станций» и привлечение всех наций к совместной работе над объединенными таким образом научными проблемами.

В воздушных полетах и полетах в пространстве доля, применяемая для мирного хозяйства и науки, еще очень мала по сравнению с долей, применяемой для целей вооружения. Но эта мирная доля в последнем десятилетии постоянно росла и, кажется, в той же степени растет и дальше, в то время как быстрое усовершенствование оружия невероятной разрушительной силы показывает все большую и большую бессмысленность его действительного применения для войны.

Мы имеем здесь замечательное историческое явление, заключающееся в том, что развитие этого оружия дальнего действия, как его двигателей и элементов, так и его приборов и боевых зарядов, является не чем иным, как развитием по очень запутанному, сложному, но действенному пути от полетов в воздухе к полетам в межзвездном пространстве.

В недалеком будущем все человечество должно будет признать, что война не только морально, но и технически бессмысленна; но тогда связанные с войной гигантские организации исследований, индустрии и армий могут рухнуть, вызвав тяжелейшее потрясение мирового хозяйства.

Еще более замечательно то, что естественным выходом из этой дилеммы является «полет в пространство», который мы не хотим считать ни гражданским, ни военным, но который, во всяком случае, не будет иметь ничего общего с архаическим понятием войн между людьми.

Полет в пространство гораздо лучше, чем современные военные воздушные полеты, удовлетворит глубокую потребность людей в приключениях, в разрядке избытка жизненных сил, в неведомых новых горизонтах.

Полет в пространство еще больше, чем современные военные полеты в воздухе и пространстве, будет нуждаться в исследовательских учреждениях, индустрии и военизированных организациях для его осуществления, но он будет при этом выполнять культурные задачи, а не будет угрожать человечеству ужасами.

Всматриваясь в завтра, мы видим пассажирские самолеты с прямоточными реактивными двигателями, позволяющими преодолевать расстояния между континентами в течение немногих часов; мы видим, как химические ракеты сооружают «внешние земные станции»; мы видим термоядерные атомные ракеты, движущиеся на межпланетных путях, и, наконец, ракеты с фотонно-ракетными приводами и прямоточными фотонно-реактивными приводами, проникающие в крайние дали Космоса на поиски наших братьев во Вселенной.

Для этих задач не хватит сил отдельной нации; нам нужны лучшие ученые, лучшие инженеры, лучшие пилоты и вся рабочая сила всех людей; нам нужно человечество, созревшее для межзвездного пространства.

Есть ли это мечта? Есть ли это неосознанная нами и внушенная нам природой цель человечества? Благосклонная и суровая природа должна знать, почему она не хочет, чтобы мы превратили наш мир в скромный рай, и почему она заставляет нас завоевывать новые миры - те последние и крайние миры, ключом к которым должны стать фотонные ракеты.

Штуттгарт, 22 сентября 1955 г.

Е. Зенгер.

Все фотонно-реактивные приводы имеют то общее, что они превращают массы горючего, находящиеся на борту, полностью или частично в кванты излучения, которые излучаются в выбранном направлении со скоростью света; тем самым, следовательно, эти приводы осуществляют максимальную возможную для реактивного привода скорость выталкивания.

Обе вышеупомянутые разновидности - фотонно-ракетный привод и прямоточный фотонно-реактивный привод - представляют собой только предельные случаи единого принципа фотонно-реактивного привода, которые отличаются тем, что ракеты с фотонно-ракетным приводом берут на борт массы горючего дискретно во время своего пребывания в подходящих местах снабжения, для того, чтобы затем в пути непрерывно их расходовать, в то время как ракеты с прямоточным фотонно-реактивным приводом берут массы горючего из окружающей среды, например из окружающей атмосферы или из окружающей межзвездной материи, непрерывно, для того чтобы также непрерывно их расходовать.

Из этого определения тотчас вытекает, что уже обычный химический прямоточный реактивный привод в атмосфере нельзя считать чистым прямоточным реактивным приводом, поскольку он непрерывно берет из окружающей среды, а именно из воздуха, только около 94-98% своего горючего, а остальное берет в форме горючих веществ, дискретно взятых на борт в подходящих местах снабжения, как это делает, впрочем, всякий экипаж.

Техническое развитие фотонно-реактивных двигателей будет, по-видимому, стремиться к тому, чтобы одновременно применять в самом двигателе оба принципа действия, причем в зависимости от потребности будет преобладать в действии один или другой. Например, во время относительно кратковременного периода ускорения или периода торможения при атмосферном, межпланетном или межзвездном полете предпочтительнее применять рабочий процесс фотонно-ракетного привода, а во время длительного периода путешествия предпочтительнее применять рабочий процесс прямоточного фотонно-реактивного привода, подобно тому как это имеет место сегодня для самолетов воздушного полета с химическим прямоточным реактивным приводом, которые стартуют при помощи ракетного действия, а полеты проводят на 96% при помощи чистого прямоточного реактивного действия.

Исследовательские работы по фотонно-реактивному приводу должны направляться прежде всего на следующие пять основных пунктов:

Для исследования механических процессов фотонно-реактивного привода (например, толчка, расхода горючего, коэффициента полезного действия, скорости выталкивания, ускорения ракеты, ее скорости, проходимого ею пути и т. д.) недостаточно законов классической механики, для этого надо прибегнуть к релятивистской механике. С ее помощью удается развить обширную теорию привода, которая охватывает все технические и природные процессы приведения в движение - от прямоточных фотонно-реактивных двигателей и фотонно-ракетных двигателей через электрические, ядерно-химические и химические реактивные двигатели вплоть до колесных двигателей и биологического приведения в движение.

Этот первый пункт программы исследования фотонно-реактивного привода является темой настоящей работы.

На первый взгляд полное превращение вещества в излучение, т. е. полное превращение массы покоя в энергию движения, представляется для фотонно-реактивных двигателей наиболее подходящей реакцией сгорания. Выход энергии, равный единице, в реакции масс искусственно достигнут до сих пор только в известной реакции электрон-позитрон, но при космических процессах и в космическом излучении он, по-видимому, достижим также и для тяжелых частиц. Так как при приеме масс очень быстрыми ракетами с прямоточным фотонно-реактивным приводом имеют место похожие условия столкновения, для них кажется не исключенной возможность искусственного осуществления полного превращения в излучение тяжелых частиц, подобно тому как это имеет место для электронов.

Этот идеальный процесс технически еще не осуществлен, поэтому и реакции с меньшим выходом энергии, такие, как термоядерные реакции или уже широко технологически освоенные ядерные реакции деления, должны быть исследованы как источники энергии для фотонно-реактивных приводов.

При выполнении весьма широкой программы исследований фотонно-реактивных двигателей на испытательных стендах можно даже возвратиться к классическим источникам энергии химических реакций.

Во всех этих случаях энергия сначала существует, по-видимому, не в желательной форме энергии фотонов средней длины волны, а в форме электрической, тепловой, кинетической энергии или энергии фотонов очень малой длины волны, так что необходимо также соответствующее превращение одного вида энергии в другой.

Техническое применение фотонных лучей как средства приведения в движение предполагает световое давление, равное по порядку величины одной атмосфере, и, следовательно, интенсивность излучения, равную по порядку величины 1 млн. ккал/см²·сек, что соответствует температуре черного излучения примерно в 150 000°К.

Каким образом устанавливаются такие интенсивности излучения, как равновесное излучение оптически бесконечно толстого раскаленного газового слоя или как люминесцентное излучение, в особенности спонтанное излучение газов, - представляет собой дальнейшую фундаментальную проблему фотонного привода.

Фотоны, несущие импульс, выходят из источника излучения сначала по всем направлениям пространства, так что их результирующий импульс практически будет равен нулю. Поэтому фотоны должны направляться подходящим рефлектором в одном желательном направлении, подобно тому как это делается в прожекторе.

Управление излучением должно сводиться главным образом к полному отражению от подходящей зеркальной поверхности и составляет, таким образом, проблему физики граничных поверхностей.

Нужные для фотонно-реактивных приводов высокие интенсивности излучения ожидаются только от крайне горячих газовых плазм. Эти газы могут быть доведены до требуемой плотности только в сосуде с крепкими стенками, подобно тому как это имеет место в известной газоразрядной лампе.

В этом случае стенки сосуда должны, конечно, обладать необычайно высокой степенью пропускания излучения, чтобы в короткое время не нагреться в недопустимой степени поглощаемой частью излучения.

Исследование и конструкция таких, в высшей степени пропускающих излучение, стенок сосуда составляют пятую фундаментальную проблему фотонно-реактивного привода.

Проблемы (г) и (д) отражения и поглощения излучения в этом существенно противоположны проблеме (в) излучения газа, поскольку в них оказываются благоприятными лишь определенные длины волн излучения.

В то время как рассматриваемая в настоящей работе первая фундаментальная проблема механики привода доступна исключительно теоретическому исследованию средствами релятивистской механики, для остальных четырех проблем к исчерпывающему теоретическому рассмотрению методами релятивистской теории, квантовой физики, ядерной физики и атомной физики должна быть присоединена обширная программа экспериментальных исследований, детали которой должны быть установлены в процессе предварительных теоретических работ.

Фиг. 1 схематически представляет процесс приведения в движение и одновременно дает важнейшие применяемые обозначения.

Во второй графе показана масса самой ракеты, справа от нее (в графе 1) показаны массы, принимаемые в ракету при процессе приведения в движение, слева от нее, раздельно, массы, отдаваемые с борта при процессе приведения в движение, а именно бортовые массы, отдаваемые без скорости относительно ракеты (графа 4), и бортовые массы, выталкиваемые ускоренно, со скоростью относительно ракеты (графа 5).

Наконец, в графе 3 представлены эксцентрично (вне оси) внешние массы, скользящие мимо ракеты, которые, однако, при скольжении получают ускорение.

Некоторые конкретные примеры позволяют сделать эту схему более наглядной.

Чистый ракетный двигатель в свободном от тяжести и сопротивления пространстве работает только с массой ракеты (графа 2) и бортовой массой (графа 5), отдаваемой с ускорением.

В случае чистого ракетного двигателя в атмосфере играют роль еще соускоряемая вследствие процесса сопротивления воздуха внешняя масса части окружающего воздуха (графа 3) и ускорение массы самой планеты.

Прямоточный реактивный двигатель в межзвездном пространстве работает с принимаемой в ракету из окружающего пространства межзвездной материей (графа 1), собственной массой ракеты (графа 2) и с отдаваемой без скорости (графа 4) или ускоренно (графа 5) бортовой массой. При сопротивлении полету в межзвездной материи может также играть роль и графа 3.

Фиг. 1. Схема приведения в движение.

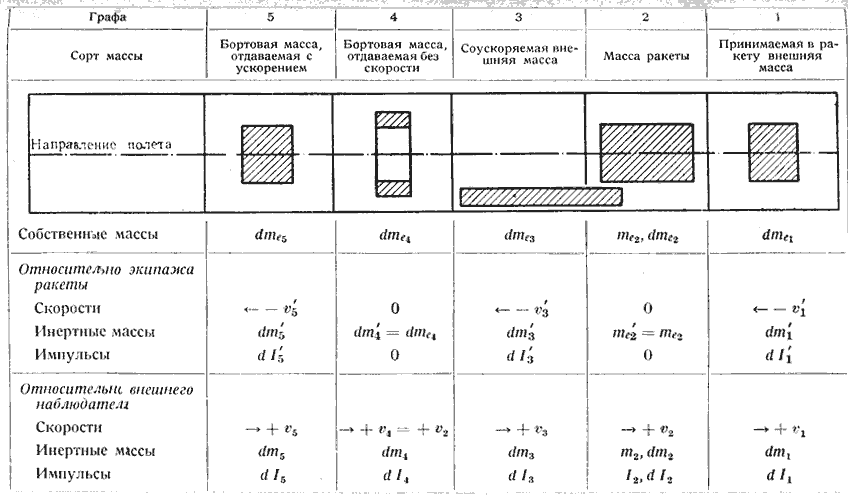
Для воздушно-реактивных двигателей в атмосфере все соотношения в основном такие же, за исключением того, что выпадает графа 4.

В работе колесного экипажа, приводимого в движение двигателем внутреннего сгорания, участвуют массы воздуха, принимаемые в него из окружающей атмосферы (графа 1), собственная масса экипажа (графа 2), масса Земли, которой сообщается толчок от колес (графа 3), ускоряемые благодаря сопротивлению воздуха массы окружающей атмосферы (также графа 3) и, наконец, отдаваемые наружу, практически без скорости, массы отработавшего газа (графа 4).

Для обычного водного или воздушного экипажа имеют место подобные же соотношения, только в механике процесса приведения в движение вместо очень большой массы Земли надо подставить соответствующие, гораздо меньшие, массы воды или воздуха, которые, опять-таки, в конце концов, передают изменения их импульса Земле.

Пешеход точно так же, как и каждое животное, работает с массой собственного тела (графа 2), с массой всей Земли (графа 3) и в некоторых случаях еще с сопротивлением воздуха (также графа 3).

Мы и в дальнейшем не будем терять из виду это механическое единство всех процессов приведения в движение пешехода, велосипедиста, гребной лодки, колесного экипажа, винтового парохода, пропеллерного самолета, воздушно-реактивного самолета и ракеты вплоть до крайних ее форм - ракеты с фотонно-ракетным двигателем и ракеты с прямоточным фотонно-реактивным двигателем.

Прежде всего мы рассмотрим с помощью релятивистской механики прием массы (графа 1) и отдачу массы (графа 4 и 5) как с точки зрения экипажа ракеты, так и с точки зрения внешнего, например, жестко связанного с местом старта наблюдателя.

Если установленная экипажем собственная масса ракеты или масса покоя m_e2 движется относительно внешнего наблюдателя со скоростью v₂ вправо (положительное направление скорости), то инертная масса или масса движения ракеты т₂ в релятивистском смысле для наблюдателя в момент наблюдения может быть найдена из соотношения

Согласно принципу эквивалентности энергии Е и массы т в формулировке Эйнштейна

Е = тс², (2.2)

Эта кинетическая энергия, которая имеется у рассматриваемого тела только по отношению к системе координат соответствующего наблюдателя, как известно, равна

В действительности, т. е. если смотреть с самого тела, вещество тела, конечно, вообще не изменяется.

Пусть эти массы движутся относительно ракеты так, что составляющая их скорости в направлении движения в момент наблюдения равна v'₁.

Экипажу ракеты плотность этих масс кажется большей, чем , с одной стороны, потому, что массы, содержащиеся в собственной единице пространства, кажутся увеличивающимися в отношении (1-v'₁/с²)^-1/2, согласно формуле (2.1), с другой же стороны, потому, что собственная единица объема V_e сама сокращается вследствие релятивистского сокращения длин l/l_e в направлении движения в отношении

Благодаря этому плотность окружающих масс при движении для экипажа будет

Поэтому масса пространства, попадающая в единицу собственного времени t_e экипажа на приемную поверхность F ракеты, равна с точки зрения экипажа

Собственная масса этого количества, которая относительно экипажа имеет скорость v'v согласно формуле (2.1), составляет

По обобщенному закону сохранения энергии, эта кинетическая энергия не может, однако, исчезнуть, а должна проявиться в ракете в какой-либо форме, такой, как нагревание, термическое возбуждение, ионизация, материализация и т. п., так что эквивалентная ей масса E_Кин/с² проявится в ракете как добавочная собственная масса.

Поэтому масса, принимаемая в ракету в одну секунду и застопориваемая там в качестве массы покоя или собственной массы, будет равна сумме собственной массы движущейся относительно ракеты материи и массы, эквивалентной ее кинетической энергии, а это и есть, согласно формуле (3.3), как раз масса, попадающая на приемную поверхность в одну секунду

Импульс, передаваемый ракете в направлении полета вместе с принимаемой массой, равен

Очень интересный предельный случай этого секундного приема масс в ракету с точки зрения экипажа имеет место тогда, когда принимаемые массы состоят из фотонов, или квантов света, и, следовательно, v₁ = с.

Так как фотоны имеют, согласно уравнению (2.1), собственную массу, равную нулю, то собственная плотность непременно будет равна нулю, между тем как плотность движения излучения имеет конечную и определенную величину, которая, например, для линейного одномерного потока фотонов выражается через массу потока М в виде = М/с, через импульс потока I в виде = I/с² и через энергию потока Е в виде - Е/с³. Для трехмерного фотонного газа соответствующие соотношения, как известно, таковы : = 4М/с - 4I/с² = 4E/с³.

Это своеобразное соотношение между собственной плотностью и плотностью движения фотонных масс, как сразу видно, совместимо с соотношением (3.2).

Принятая в одну секунду в ракету масса, согласно формуле (3.6), равна в этом случае

dm'_e1/dt_e = Fc. (3.6а)

Длинноволновые фотоны, энергия которых по закону эквивалентности соответствует массе, представляемой формулой (3.6а), будут, напротив, большей частью вызывать только нагревание, термическое возбуждение, диссоциацию, ионизацию и т. д.

Следовательно, импульс, передаваемый ракете в направлении полета с принимаемой массой фотонов, составляет

dl'₁/dt_e = cdm'₁/dt_e = Fc². (3.7а)

Мы рассмотрим теперь тот же самый процесс приема массы, но уже не с точки зрения экипажа ракеты, а с точки зрения внешнего наблюдателя, относительно которого ракета движется в рассматриваемый момент со скоростью v₂, причем каждая отложенная вправо скорость опять будет рассматриваться как положительная.

Соотношения для новой системы получаются из соотношений предыдущей главы с помощью известных преобразований Лоренца. Из них следует, например, релятивистская теорема сложения скоростей, которая позволяет вычислить скорость v₁ невозмущенных масс среды относительно внешнего наблюдателя из измеренных в системе наблюдателя скорости Δv₁ относительно ракеты и скорости ракеты v₂:

В случае v₂ = О величина v₁ = Δv₁ идентична величине v'₁ предыдущей главы.

В случае Δv₁ = с будет также v₁= с, точно так же, как в случае v₂ = с.

В случае Δv₁ = 0 будет v₁ = v₂.

Из уравнения (4.1) непосредственно следует

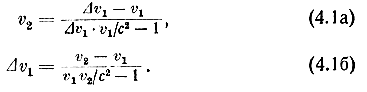
Важнейшие частные случаи этого последнего уравнения приведены в табл. 1. Например, если v₁ и v₂ равны и направлены в одну сторону, то относительная скорость Δv₁ непременно будет равна нулю, за исключением того случая, когда v₁ = v₂ =± с. В последнем случае, если обе скорости направлены противоположно, то скорость Δv₁ масс среды относительно ракеты, измеренная в системе наблюдателя, равна, однако, только скорости света с точно так же, как если бы они были направлены одинаково.

В соответствии с формулой (3.2) плотность невозмущенных масс среды кажется нашему наблюдателю теперь равной

В предельном случае Δv₁ = 1 плотность движения фотонного газа должна быть одинакова для наблюдателя в ракете и для внешнего наблюдателя, Так как относительно обоих наблюдателей газ имеет одну и ту же скорость, а именно скорость света. Роль скорости света как предельно большой скорости ясно выступает в явлении.

Масса среды, попадающая в единицу времени внешнего наблюдателя на приемную поверхность F ракеты, кажется этому наблюдателю равной

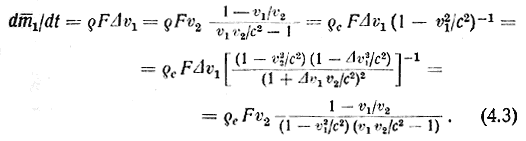
Таблица 1

Частные случаи относительной скорости Δv₁ между массами пространства и ракетой

Отрицательные знаки в табл. 2 означают, что массы среды попадают на ракету спереди, положительные знаки - что они попадают на нее сзади, согласно принятому определению положительных направлений скоростей.

При v₂/c = 0 соотношения (4.3) переходят, естественно, в соотношения (3.3).

В предельном случае, когда v₁/c = ± 1, следовательно, при Δv₁/с= ± 1 будет dm₁/dt = ± Fc, кроме случая, когда