вернёмся в начало?
Часть II. НАШИ СРЕДСТВА БОРЬБЫ
Глава III. Пушки
1. Пушечный выстрел
2. Современные достижения артиллерии. Сверхдальнобойные оридия
3. Проблема выстрела их пушки на Луну
Под выстрелом мы понимаем выбрасывание снаряда из канала орудия давлением газов, находящихся за ним в совершенно замкнутом пространстве, образующихся при взрыве пороха или иного вещества. Те исключительные результаты, которые техника постройки артиллерийских орудий достигла в последние годы мировой войны, в памяти у всех еще достаточно свежи. С помощью современных дальнобойных артиллерийских орудий были достигнуты наибольшие скорости в 1 500 - 1 600 м/сек, когда-либо сообщенные телу по воле человека. Таким образом эти орудия названного типа явились наиболее мощными машинами из всех существующих.
1. Пушечный выстрел
Теоретически не представляет никакого затруднения рассчитать пушку, снаряд который смог бы долететь до Луны. По законам внутренней баллистики* при этом играют роль следующие величины: длина канала ствола как длина пути, на котором может быть произведено ускорение, среднее давление внутри канала как сила, с которой пороховые газы толкают снаряд вперед, поперечная нагрузка снаряда как масса, находящаяся над (или перед) каждым квадратным сантиметром поперечного сечения калибра и противостоящая действию ускорения присущей ей инерцией. Отсюда следует, что для достижения возможно более высокой скорости при вылете из канала ствола он должен быть взят возможно более длинным, среднее давление в нем наиболее высоким, а поперечная нагрузка наиболее малой (рис. 23).
* Баллистика - наука, изучающая движение артиллерийских снарядов и пуль. Она разделяется на две отрасли: внутреннюю и внешнюю баллистику. Первая рассматривает явления, происходящие в канале ствола при выстреле, а вторая - явления, происходящие со снарядом или пулей после вылета их из канала ствола. (Прим. ред.)
На практике же конструктору пушек во всех этих направлениях поставлены довольно тесные границы.
Длина ствола уже потому не может быть сделана произвольно большой, что вследствие охлаждения пороховых газов в результате их расширения и соприкосновения с холодными стенками ствола вскоре наступает такое положение, при котором падающая сила давления пороховых газов целиком поглощается трением, испытываемым снарядом при прохождении последним канала ствола.
Равным образом и среднее давление пороховых газов, являющееся вторым наиболее важным фактором, играющим роль при выстреле, заключено в довольно тесных пределах.
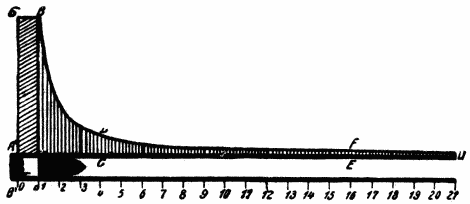
Рис. 23. Идеальная кривая давления пороховых газов, построенная в предположении, что весь заряд воспламеняется мгновенно,
а расширение газа происходит адиабатически. В действительности давление достигает наивысшего значения не в самом начале,
но лишь позднее и кроме того далеко не достигает теоретического значения.
Свойства взрывчатого вещества определяются в первую очередь его химическим составом, а во вторую очередь - способом его механической обработки. Порох одинакового химического состава может сгорать совершенно различным образом в зависимости от того, какая ему придана форма в процессе его обработки. Порох может изготовляться в форме пороховой муки, или, как ее иначе называют, мякоти, зерен, пластинок, кубиков, стержней или трубок. Теоретические свойства взрывчатого вещества определяются, главным образом, следующими понятиями: их теплотворной способностью; их удельным газовым объемом, их температурой взрыва, объемом пороховых газов, образующихся в процессе взрыва, и давлением этих газов.
Удельным давлением взрыва мы, по Бертло, называем то идеальное давление, которое возникло бы в пространстве объема в 1 л. при взрыве в нем 1 кг. взрывчатого вещества.
В этом случае плотность заряда, показывающая, сколько килограммов взрывчатого вещества может быть помещено в пространстве одного литра камеры взрывания, равна единице. Обыкновенно у артиллерийских орудий она достигает значений всего лишь в 0,4 - 0,7, а у ружей в 0,70 - 0,85. Во всяком случае плотность заряда никогда не может превосходить плотность или, иными словами, удельный вес самого взрывчатого вещества, потому что мы не можем набить камеру взрывания большим количеством пороха, чем в нее может войти в виде твердой монолитной массы.
Ввиду важности некоторых встречающихся значений в том числе и для разбираемых ниже проблем ракеты мы приводим их сгруппированными в следующей таблице 10.
Таблица 10
| Название взрывчатого вещества | Черный порох | Пласти-
нчатый порох | Пиро-
ксилин | Нитро-
глицери-
новый порох | Порох для дально-
бойных орудий | Гремучая ртуть |
| 1. Теплотворная способность в кал./кг. | 685 | 630 | 1 100 | 1 290 | ~ 1 400 | 410 |
| 2. Удельный газовый объем в л. | 285 | 920 | 859 | 840 | ~ 999 | 314 |
3. Температура
взрыва, °С | 2 770 | 2 400 | 2 710 | 2 900 | ~ 3 300 | 3 530 |
| 4. Объем взрывных газов в л. | 3 177 | 9 008 | 9 386 | 9 763 | 12 957 | 4 374 |
| 5. Удельный вес | 1,65 | 1,56 | 1,50 | 1,64 | 1,6 | 4,4 |
| 6. Давление газов в am., при плотности заряда | | | | | | |
= 0,1 | 336 | 542 | 1061 | 1098 | 983 | 468 |
= 0,2 | 708 | 1217 | 2343 | 2351 | 2174 | 966 |
= 0,3 | 1123 | 2077 | 3931 | 3947 | 3650 | 1501 |
= 0,4 | 1587 | 3211 | 5912 | 5640 | 5523 | 2072 |
= 0,5 | 2112 | 4779 | 5802 | 7829 | 7982 | 2686 |
= 0,6 | 2708 | 7082 | 12000 | 10560 | 11350 | 3347 |
= 0,7 | 3393 | 10800 | 17020 | 14 080 | 16240 | 4 052 |
= 0,8 | 4201 | 17 870 | 21810 | 21 520 | 24030 | 4952 |
= 0,9 | 5126 | 86 250 | 38 500 | 25270 | 38310 | 5683 |
= 1,0 | 6236 | - | - | 35 010 | - | 6603 |
=1,6 | 29 340 | - | - | - | - | 14560 |
= 2.4 | - | - | - | - | - | 43 970 |
Поперечная нагрузка, являющаяся третьим наиболее важным фактором, так же как и форма снаряда, не влияет на форму пути в безвоздушном пространстве. Здесь играет роль единственно лишь скорость при вылете из канала ствола.
Форма пути снаряда, летящего в безвоздушном пространстве, является почти в точности параболической. Расчет путей артиллерийских снарядов в атмосфере принадлежит к числу наиболее сложных и трудных проблем внешней баллистики. Поэтому мы не можем входить здесь ни в какие подробности. В качестве интересного цифрового примера мы приводим в нижеследующей таблице 11 данные, вычисленные на основе точных формул, характеризующие полет снаряда сверхдальнобойного орудия, стреляющего на 126 км.
Таблица 11
| Сверхдальнобойное орудие | Наклон полета к гори-
зонту в град. | Дальность полета в км. | Наибольшая высота в км. | Скорость снаряда в м/сек. | Продол-
жительность полета в сек |
| Момент выстрела | 54 | 0,00 | 0,03 | 1500 | 0,0 |
| | 53 | 3,45 | 4,67 | 1300 | 4,3 |
| | 50 | 10,83 | 14,00 | 1060 | 14,3 |
| | 45 | 19,70 | 23,72 | 930 | 27,3 |
| | 40 | 26,80 | 30,33 | 860 | 38,2 |
| | 25 | 43,07 | 41,04 | 720 | 62,1 |
| Момент пролета через высшую точку | 0 | 63,84 | 46,20 | 650 | 94,5 |
| | 25 | 83,55 | 41,60 | 714 | 120,0 |
| | 40 | 99,06 | 31,20 | 840 | 150,5 |
| | 50 | 115,99 | 16,60 | 950 | 173,3 |
| | 53 | 122,00 | 6,12 | 945 | 191,0 |
| | 58 | 126,00 | 0,00 | 860 | 199,0 |
Подлинное величие этих цифр во всей его убедительности проявляется, правда, лишь тогда, когда мы достроим кривую полета этого снаряда и для сравнения нанесем в том же масштабе высочайшие горные вершины и достигнутые до сего времени рекорды высоты (рис. 24). На 46 200 м поднялся бы снаряд уже при выстреле на наиболее далекое расстояние и приблизительно на 70 000 м он смог бы подняться при вертикальном выстреле вверх! Чем по сравнению с этим является Эверест - одна из высочайших горных вершин высотою в 8 884 м! И лишь за 3 мин. 20 сек. этот снаряд пролетел бы свой путь длиною в 150 км.
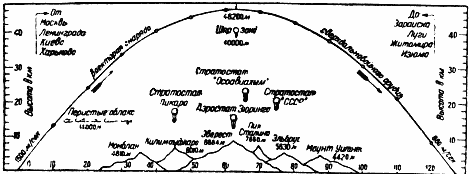
Рис. 24. Кривая полета снаряда сверхдальнобойного орудия.
Для оценки возможности производства горизонтального выстрела в мировое пространство прибавим, что согласно исследованиям иаиболее крупных баллистиков в данном случае является безразличным, как будет расположена масса воздуха вдоль пути снаряда. В силу этого при расчете общего замедления, претерпеваемого снарядом, выпущенным в мировое пространство, мы могли бы внести в наше вычисление вместо истинной так называемую однородную изометрическую атмосферу высотою в 7 800 м. Такая атмосфера снизу доверху обладала бы плотностью воздуха на уровне моря и столб ее высотою в 7 800 м содержал бы ту же массу воздуха, что и столб истинной атмосферы того же поперечного сечения.
2. Современные достижения артиллерии.
Сверхдальнобойные орудия
Для сравнения с проблемой пушки, стреляющей на Луну, имеет смысл привести обзор современных достижений артиллерии в форме сводной таблицы 12. Кроме того в связи с этим будет не лишним сообщить некоторые сведения из истории развития дальнобойных пушек, могущих служить ближайшим прототипом пушки, способной послать снаряд на Луну, поскольку до сего времени достижения наивысших скоростей вылета из канала ствола осуществимы именно с их помощью.
Разумеется, уже издавна все воюющие государства стремились строить возможно более дальнобойные пушки. Причина этого ясна: чем сильнее разрушительное действие гранат и чем больше дальность их попадания, тем в большей степени можно было считать военную мощь своей армии не уступающей или же превосходящей военную мощь противника.
В печати существуют указания на то, что французское артиллерийское ведомство уже в 1895 г. производило опыты с 16,5-сантиметровой пушкой длиною в 100 калибров, причем была достигнута скорость вылета снаряда из канала ствола в 1 200 м/сек. В Германии первым толчком для практического развития дальнобойной артиллерии послужил опыт стрельбы, произведенный Круппом, во время которого граната 24-сантиметрового орудия против ожидания его конструктора пролетела 48 км вместо 32 км. Кроме того в Англии и в других странах в специальных журналах по артиллерии был описан ряд проектов сверхдальнобойных орудий, повидимому, так и оставшихся на бумаге. Гораздо большего внимания заслуживает тот факт, что французская артиллерия, начиная с 1924 г., располагает орудиями, стреляющими тяжелыми гранатами весом в 180 кг на расстоянии в 120 км, при весе заряда нитроглицеринового пороха всего лишь в 160 кг. Скорость вылета снаряда из канала ствола составляет при этом всего лишь 1 450 м/сек. Равным образом и длину ствола этой пушки, равную всего лишь 23,1 м при калибре ее в 21,1 см., следует признать весьма незначительной.
Тем не менее результат, достигнутый германскими конструкторами сверхдальнобойных орудий профессором Раузенбергером и профессором Эберхартом во время мировой войны, повидимому, может считаться непревзойденным до настоящего времени. Как известно, предельная дальнобойность сконструированного ими орудия составляла 135 км.
Для этого весивший 142 т ствол длиною в 36 м пришлось составить из трех кусков: из трубы диаметром в 38 см, из вставленного в нее нарезного ствола с диаметром калибра в 21 см и из ненарезной насадки. Для предотвращения нагибания этого составного ствола части его были подвешены к мостообразной форме. Несмотря на это, под действием невероятной силы взрыва заряда нитроглицеринового пороха весом в 180 - 300 кг, извергавшего из канала ствола снаряд весом около 100 кг со скоростью, доходившей до 1600 м/сек, ствол в продолжение двух минут после выстрела дрожал как тростинка, колеблемая ветром.
Таблица 12
| Данные | Типы орудий |
| винтовка | полевое орудие | морское орудие | дально-
бойное орудие | береговое орудие | английское дально-
бойное орудие |
| Калибр в см. | 0,79 | 7,5 | 21,0 | 21,0 | 40,64 | 50,8 |
| Сечение калибра в см2 | 0,49 | 44,2 | 340,4 | 346,4 | 1297,10 | 2026,8 |
| Длина канала в калибрах | 101,50 | 26,7 | 50,0 | 150.0 | 50,00 | 100,0 |
| Длина канала в м. | 0,80 | 2,0 | 10,5 | 33,6 | 20,30 | 50,8 |
| Длина ствола в калибрах | 116,52 | 28,7 | 55,0 | 171,0 | 52,50 | 105,0 |
| Длина ствола в м. | 0,90 | 2,2 | 11,0 | 36,0 | 21,40 | 53,7 |
| Все ствола в кг. | 1,00 | 310,0 | 15450,0 | 142000,0 | 113100,00 | 550000,0 |
| Вес снаряда в кг | 0,01 | 6,5 | 125,0 | 100,0 | 920,00 | 2 000,0 |
| Скорость вылета в м/сек | 900,00 | 600,0 | 940,0 | 1600,0 | 940,00 | 1340,0 |
| Дальнобойность в км. | 4,00 | 9,0 | 26,0 | 130,0 | 40,0 | 160,0 |
| Кинетическая энергия при вылете в тоннометрах | 0,413 | 119,3 | 5629,0 | 15360,0 | 41440,00 | 183000,0 |
| То же в кгм | 413 | 383,9 | 364,0 | 108,0 | 366,00 | 333,0 |
| Средняя сила тяги в кг. | 516 | 59700,0 | 534 850,0 | 457140.0 | 2 039 400,00 | 3 602 400,0 |
| Среднее давление в am. | 1053 | 1350,0 | 1544,0 | 132,0 | 1572,00 | 1 777,0 |
| Среднее время пролета ствола в секундах | 1/563 | 1/150 | 1/46 | 1/23 | 1/23 | 1/13 |
| Средняя мощность в л.с. | 3100 | 238600,0 | 3359500,0 | 473200,0 | 12780000,00 | 32780 000,0 |
| Средняя мощность на вес ствола с л.с./кг. | 3100 | 769,7 | 217,4 | 33,35 | 115,63 | 58,24 |
Однако является в высшей степени вероятным, что и это огромное достижение сверхдальнобойной артиллерии* еще не исчерпало возможностей германских конструкторов. Можно думать, что если бы мировая война продлилась еще год ими были бы достигнуты скорости вылета снарядов из орудия в 1 700 - 1 800 м/сек и вместе с этим и дальнобойность в 200—250 км. В пользу такого предположения говорят следующие соображения. Несколько более длинный ствол несомненно мог бы быть построен. Химия взрывчатых веществ, по мнению Штетбахера, имела возможность повысить теплотворную способность наиболее сильных в то время нитроглицериновых порохов (достигавшую 1 290 кал/кг при 40-процентном содержании нитроглирина) еще выше - почти до предельного значения для взрывчатого желатина (в 1 620 кал/кг при 92-процентном содержании нитроглицерина и 8-процентном содержании пироксилина). При этом существовала возможность путем смягчающего действия примеси гексанитроэтана и аналогичных ему химических веществ устранить опасное свойство пироксилина мгновенно взрываться и создать нужный для поставленной цели медленно горящий порох.
* Называемой также «суперартиллерией». (Прим. ред.)
3. Проблема выстрела из пушки на Луну
Лишь после сообщения приведенных сведений о пушках, возможно, наконец, перейти к обсуждению проблемы выстрела из пушки на Луну. При этом мы произведем критическую оценку того, в какой степени смелый проект, подробно описанный Жюлем Верном в его знаменитом романе «От Земли до Луны», соответствует современным воззрениям баллистики. Представляется несомненным, что Жюль Верн перед написанием этого романа воспользовался советами и указаниями наиболее крупных специалистов своего времени, а не занимался - как это часто предполагается - сообщением совершенно фантастических цифр подобно многим из числа своих последователей.
а) Колумбиада «Пушечного клуба»
В первой главе своего романа Жюль Верн представляет читателю «Пушечный клуб» как общество фанатических артиллеристов, члены которого «пользуются уважением прямо пропорциональным квадрату дальнобойности изобретенных ими пушек». Во второй главе описывается чрезвычайное общее собрание, на котором президент клуба Барбикэн, для того чтобы утешить членов в том, что на Земле уже отсутствует возможность войны, и чтобы разжечь их баллистическое самолюбие, делает им предложение осуществить перелет на Луну в пушечном ядре. Кульминационным моментом речи является ее конец, в котором Барбикен выражает уверенность в знании членами пушечного клуба того, что прочности пушек и силе пороха нет пределов, после чего оратор заканчивает свою речь такими словами: «Рассмотрев вопрос со всех сторон и тщательно проверив все свои выводы, я сделал строго научное заключение, что всякий снаряд, посланный на Луну с начальной скоростью в 12 000 ярдов в секунду, непременно должен, достичь этого светила. Вот почему, уважаемые коллеги, я и созвал вас на собрание - я предлагаю вам проделать этот небольшой опыт». 12 000 ярдов равняются приблизительно 11 200 м. Как мы видим, Барбикэн правильно уловил самую сущность дела.
В главе III описывается, как сообщение Барбикэна подействовало на публику. В главе IV сообщается заключение Кэмбриджской обсерватории относительно астрономической части затеваемого предприятия. Мы приводим вкратце вопросы и ответы (с переводом всех величин в метрические меры.
1. Возможно ли перебросить ядро с Земли на Луну?
- Ответ: Да, если сообщить ему начальную скорость в 11 200 м/сек.
2. Каково точное расстояние Луны от Земли?
- Ответ: Оно колеблется из-за эксцентриситета лунной орбиты. Наименьшее из возможных расстояний между центрами этих двух светил равняется 357 000 км. Вычтя отсюда земной и лунный радиусы (6 378 км. и 1 735 км), мы получим наименьшее расстояние между ближайшими друг к другу точками поверхностей этих тел, равное 348 900 км
3. Во сколько времени снаряд, посланный с достаточной начальной скоростью, пролетит это расстояние и, следовательно, в какой именно момент необходимо выпустить этот снаряд, с тем чтобы он упал на Луну к определенному сроку?
- Ответ: Снаряд потратит на перелет 97 час. 13 мин. 20 сек. Именно на такой срок времени нужно будет выстрелить раньше того момента, в который снаряд должен упасть на Луну.
4. Когда Луна находится в наиболее благоприятном для этого положении?
- Ответ: Когда она находится в перигее (т.е. ближе всего к Земле) и в то же время в зените орудия
5 В какую точку неба следует направить орудие?
- Ответ: В зенит; в силу этого орудие следует установить в такой местности, в зените которой Луна вообще когда-либо может находиться, т.е. в местности между 28 северной и южной широты.
6. В каком месте должна находиться Луна в то мгновение, когда будет произведен выстрел?
- Ответ: На расстояния 64° от зенита, потому что именно на столько она успеет переместиться за эти 97 час. с лишним (здесь учтено также и то отклонение, которое получит ядро вследствие вращения Земли).
Как видно, Жюль Верн стремится ваять наиболее простой случай, для того чтобы представить читателю все дело в возможно более понятной форме. Он хочет выстрелить в движущуюся по своей орбите Луну, взяв несколько вперед, как охотник стреляет в зайца из медленно движущейся повозки, когда ему приходится учитывать и скорость движения этой повозки. Снаряд должен лететь от Земли до Луны почти по прямой линии. В действительности же, как это может быть установлено путем построения параллелограммов скорости для всех точек пути, снаряд опишет кривую с одной точкой перегиба, похожую на латинскую букву S (рис. 25), это произойдет вследствие совместного действия на снаряд вращения Земли и толчка от выстрела.
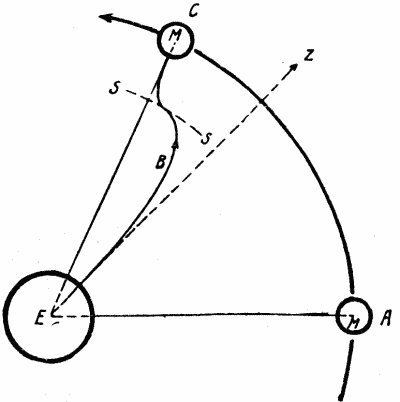
Рис. 25. Путь снаряда, который Пушечный клуб собирался послать на Луну.
Z - направление, в котором был произведен выстрел в тот момент, когда Луна находилась в точке А. С - положение Луны, в котором ее настигнет снаряд. В - путь снаряда. S-S - граница сферы земного притяжения между Землей и Луной. (Чертеж выполнен схематично, без соблюдения масштаба).
В главе VII начинаются прения относительно ядра. Нельзя сказать, чтобы они велись особенно деловито. Чувство воодушевления играет в них решающую роль. Величина, т.е. наружный диаметр ядра (первоначально разговор идет только о круглом ядре, но не о продолговатом снаряде), определяется условием, в силу которого оно могло бы быть видимым вовремя своего движения, а также и в момент падения на Луну. Президент Пушечного клуба Барбикэн рассчитывает при помощи имеющего быть сооруженным и установленным на высочайшей горе Америки огромного зеркала достичь 48 000-кратного увеличения и благодаря этому разглядеть на поверхности Луны тело диаметром в 9 футов. Поэтому и диаметр ядра должен равняться 9 футам (108 американским дюймам по 25 мм = 2,70 м). Такое увеличение, разумеется, немыслимо, но это в данном случае не играет существенной роли. Достаточно наполнить ядро порохом, который разом вспыхнул бы при ударе снаряда о лунную поверхность. Это явилось бы столь же надежным доказательством попадания снаряда на Луну, и притом разглядеть такую вспышку гораздо легче, чем сам снаряд. Заметим, что американский профессор Годдард предполагает снабдить свои ракеты порохом для такой именно вспышки
Заседание продолжается.
Сначала предлагается отлить сплошное чугунное ядро. Но это пугает майора Эльфистона. Затем Барбикэн предлагает сделать ядро полым внутри, благодаря чему оно весило бы только 2,5 т. Наконец все приходит к общему решению построить пустотелое алюминиевое ядро весом 20 000 фунтов или в 10 т. Стенки этого ядра должны быть толщиною в 12 дюймов. В конце прений членов собрания приводит в смущение вопрос о стоимости «опыта», потому что алюминий расценивается Жюлем Верном по тогдашней цене в 9 долларов за фунт. В настоящее время килограмм этого металла стоит меньше полтинника, так что вопрос о цене его в данном случае не мог бы теперь играть сколько-нибудь существенной роли.
В главе VIII описывается заседание комитета Пушечного клуба, обсуждающее вопрос о самой пушке. Поставленная задача ясна - необходимо ядру весом в 10 т сообщить при вылете скорость в 11 200 м/сек. Диаметр этого канала также известен, так как ядро должно иметь в поперечнике 270 см. Вопрос сводится к тому, какой длины необходимо построить орудие и какой толщины нужно сделать стенки для того, чтобы оно могло выдержать давление пороховых газов при выстреле.

Рис. 26
Вертикальный разрез
колумбиады
Барбикэна. |
Дж. Т. Мастон, неукротимый секретарь Пушечного клуба, с первых же слов требует, чтобы пушка была длиною не менее полумили (т.е. не менее 800 м, так как 1 миля = 1,61 км). Обвиненный в страсти к преувеличению, Мастон энергично стремится опровергнуть это. И действительно, он не так далек от истины. Если бы Барбикэн последовал его совету, то ядро несомненно полетело бы на Луну вернее. Председатель обращает внимание на то, что обычно пушки в 20 - 25 раз длиннее своего калибра, в ответ на что Мастон заявляет ему прямо в лицо, что с таким же успехом можно было стрелять в Луну из пистолета. Наконец все соглашаются на длине орудия, превышающей его калибр в 100 раз, т.е. равняющейся 900 футам или 270 м. Как мы увидим дальше, такая длина в действительности недостаточна. Стенки пушки предлагается сделать толщиною шесть футов, каковая величина и принимается без возражений. Пушка, занимающая вертикальное положение, должна быть отлита прямо в земле из чугуна. Дж. Т. Мастон высчитывает, что она будет весить 68 040 т. Здесь Барбикэн, очевидно, принимает, что земля, окружающая орудие, настолько сожмет его, что оно при выстреле не разорвется. Это довольно вероятно, если мы представим себе, что дуло орудия помещено в очень твердую и однородную каменную породу, как, например, в гранит, порфир и т.п. (рис. 26). Тогда отлитое из металла дуло будет, собственно говоря, являться только внутренней облицовкой настоящего каменного дула, прочность которого чрезвычайно велика и не может быть оценена нами сколько-нибудь точно.
Глава IX посвящена вопросу о порохе. Жюль Верн заставляет здесь своих героев рассуждать следующим образом: 1 л пороха весит 900 г и при взрыве выделяет 4 000 л. газа. В обыкновенных пушках вес одного заряда пороха составляет 2/3 веса снаряда, у больших же орудий эта дробь уменьшается до 1/10. Здесь Мастон высказывает мысль, что если эта теория действительно верна, то при достаточных размерах орудия для стрельбы вообще не потребуется пороха. Но заседание вновь становится серьезным и после того, как было решено воспользоваться крупнозернистым родмановским порохом, приближается момент, когда необходимо будет определить количество пороха. Тут члены комитета, беспомощно переглянувшись и не будучи в состоянии произвести точного расчета, предлагают наудачу различные количества. Член комитета Морган предлагает взять 100 т пороха, Эльфистон советует взять 250 т, а пылкий секретарь требует 400 т. И на этот раз он не только не заслужил упрека в преувеличении со стороны председателя, но последний находит и эту цифру недостаточной и требует ее удвоения, вследствие чего отношение весов ядра и пороха становится равным 1:80.
После этого членам комитета много забот доставляет огромный объем такого количества пороха. Оказывается что 800 т пороха заполнят дуло задуманного орудия наполовину, вследствие чего оно окажется слишком коротким. Наконец удается выйти из затруднения, решив воспользоваться вместо пороха пироксилином. Собрание клуба заканчивается, будучи уверено в том, что количество пироксилина, заполнившее дуло орудия на протяжении 54 м, произведет взрыв той же силы, что и 800 т пороха, первоначально предложенных Барбикэном. Таким образом и будет достигнута необходимая начальная скорость в 11 200 м/сек.
Так как общая длина ствола орудия составляет 270 м, из которых однако 54 м приходится на долю заряда пироксилином, то ядро будет двигаться внутри него на протяжении 216 м. На этом протяжении ему должна быть сообщена вся кинетическая энергия в 64 млрд. кгм, которой он должен обладать в момент вылета из канала ствола. Это число получается, исходя из веса снаряда в 10 000 кг и необходимой скорости вылета его из канала ствола в 11 200 м/сек. А отсюда мы в свою очередь получаем, что среднее давление в канале ствола будет равняться 5 175 ат, продолжительность полета в стволе 1/26 сек., а работа, произведенная таким выстрелом, - 22,2 млрд. л.с.
Относительно роли сопротивления воздуха мы у Жюля Верна находим в главе VIII только вскользь брошенное замечание, «что оно будет несущественно». Наш долг исследовать этот вопрос поточнее, потому что мы уже не раз имели случай убедиться в том, что расчеты увлекающихся членов Пушечного клуба несколько ненадежны.
Мы будем различать два рода сопротивления воздуха, а именно сопротивление столба воздуха, находящегося в канале орудия, и сопротивление всей атмосферы, которую снаряду суждено пролететь по вылете из дула пушки.
В момент выстрела над ядром Барбикэна в дуле орудия находится столб воздуха высотой в 216 м и диаметром в 2,70 м. Вся эта масса воздуха никуда в сторону уйти не может и будет подобно стальной пружине сжата снарядом, поднимающимся с огромной скоростью. Так как скорость полета снаряда в канале орудия значительно (в конце более чем в 30 раз) превышает скорость звука, то этот воздух не сможет даже уйти из отверстия дула вверх, потому что для этого не хватит времени. Короче говоря, тут дело будет обстоять так, как будто перед взлетающим ядром находится колпак или крышка этого сжатого воздуха, которая рассеется но сторонам только после вылета снаряда из дула орудия. Выражаясь языком техники, мы скажем, что снаряд должен сообщить всей массе этого воздушного столба до вылета из орудия свою собственную скорость и кроме того произвести еще работу сжатия этого же воздуха.
Объем воздушного столба, находящегося в дуле, будет равен 1 237 м3 вес его из расчета по 1,2 кг на каждый кубический метр составит на-круг 1 500 кг, т. е. примерно 1/6 веса снаряда. Для того чтобы сообщить этой массе скорость в 11 200 м/сек, необходимо произвести добавочную работу, равную почти в точности 1/6 первоначально найденного количества в 63,78 млрд. кгм. Итак, следовательно, для преодоления сопротивления воздуха, находящегося в дуле орудия, и для сжатия этого воздуха необходимо будет затратить примерно на 14 млрд. кгм больше работы, чем это было вычислено до того, как было принято во внимание сопротивление воздуха *. Припомним, что среднее давление пороховых газов, находящихся за снарядом, получилось у нас равным немногим более 5 000 ат и что это число вначале несомненно будет значительно превышено, а позднее, по мере того как снаряд будет все сильнее приближаться к отверстию дула, наоборот, не будет даже достигнуто. Благодаря этому может случиться, что еще до вылета снаряда из дула орудия все возрастающее давление сжимаемого им воздуха превысит непрерывно убывающее давление пороховых газов, находящихся позади снаряда, вследствие чего снаряд, еще находясь в дуле, был бы заторможен.
* Здесь автор несомненно преувеличивает величину сопротивления воздуха в дуле орудия, принимая, что все частицы воздуха находящиеся в дуле, приобретают полную скорость снаряда. На самом же деле такую скорость может приобрести не более половины заключающегося в дуле воздуха. (Прим. Ред.)
K счастью, этого сопротивления (столба воздуха в дуле орудия), для преодоления которого нам потребуется целых 14 млрд. кгм, можно избегнуть, если мы догадаемся непосредственно перед выстрелом выкачать из пушки воздух. Но тогда, разумеется, мы должны снабдить отверстие дула крышкой легкой, но в то же время и достаточно прочной, для того чтобы внешнее давление атмосферы не продавило бы ее. Тогда ядро, с неуменьшенной скоростью вылетающее из отверстия дула, совершенно легко расшибло бы изнутри эту крышку, затратив на это лишь несколько десятков килограммометров.
Хуже обстоит дело с сопротивлением воздуха, находящегося над пушкой. Правда, оно с момента вылета снаряда из дула будет быстро уменьшаться и уже к концу первой секунды составит всего лишь 1/5 своей начальной величины. Но все же при скорости вылета снаряда, равной 11 200 м/сек, и при коэфициенте его формы p=1/6 сопротивление воздуха составит около 230 ат. Вследствие этого барбикэновский полый алюминиевый снаряд уподобился бы мыльному пузырю, толкаемому бильярдным кием против бури.
Вследствие незначительной прочности своих стенок снаряд этот еще в дуле орудия был бы раздавлен в лепешку огромным давлением напирающих на него сзади пороховых газов и мощным сопротивлением столба воздуха, находящегося в дуле перед ним. Вполне возможно даже, что он, вследствие этого просто не смог бы вылететь из дула. Об этой последней возможности приходится подумать потому, что Барбикэн ничего не упоминает о направляющих кольцах, которые в данном случае необходимы не столько из-за нарезов, сколько ввиду растяжимости алюминия. Такие кольца должны были бы сыграть роль поршневых колец наших автомобильных моторов. Барбикэн упустил из вида, что алюминий обладает коэфициентом расширения втрое большим, чем чугун.
А кроме того такой снаряд ни в коем случае не смог бы пронизать всей толщи земной атмосферы, так как для этого его поперечная нагрузка в 10000 кг / 57 256 см2 = 175 г/см2 является совершенно недостаточной. Будучи выстрелен со скоростью в 11200 м/сек, этот снаряд, правда, приобрел бы силу в 6,4 млн. кг на 1 кг своего веса. Но в то же время на 1 см2 своего поперечного сечения он приобрел бы кинетическую энергию всего лишь в 1,12 млн. кгм, т.е. два 60% той кинетической энергии, которая должна была бы поглотиться одним только сопротивлением воздуха при условии сохранения параболической скорости. Отсюда ясно, что знаменитый снаряд Пушечного клуба в том случае, если бы он не кончил бесславно еще в дуле пушки, «застрял» бы в воздухе уже в течение первой секунды своего полета. Отнюдь не будучи в состоянии долететь до Луны, этот снаряд, даже если бы он и не расплавился, в действительности смог бы описать над Землей только смехотворно короткую дугу. Возражение подобного рода Жюль Верн приводит и в своем романе, но не развивает его дальше. По-видимому он хотел этим намекнуть достаточно сведущим своим читателям о том, что он знал, почему колумбиада Барбикэна в действительности неосуществима.
б) Проблема выстрела на Луну с точки зрения современном баллистики
О точки зрения современной баллистики прежде всего нужно рассчитать с учетом сопротивления воздуха необходимую скорость при вылете из канала ствола для заданного калибра при допустимой поперечной нагрузке и при определенной форме снаряда. При этом мы получаем два семейства расходящихся веером кривых. Часть кривых обоих этих семейств пересекается между собою, другая же часть не пересекается. Точки пересечения первой части дают нам решение поставленной проблемы при конечных скоростях вылета из канала ствола. Вторая же часть кривых свидетельствует о том, что для соответственных поперечной нагрузки и формы снаряда вообще не существует никакой сколь угодно большой скорости, при которой снаряд под действием сообщенного ему избытка (над напряжением поля земного тяготения) кинетической энергии мог бы преодолеть соответствующее сопротивление воздуха. Наивыгоднейшие решения сопоставлены в таблице 13.
| Поперечная нагрузка | 2,0 кг/см2 | 1,5 кг/см2 | 1,0 кг/см2 | 0,75 кг/см2 | 0,5 кг/см2 | 0,33 кг/см2 |
| Скорость при вылете V | км/сек | км/сек | км/сек | км/сек | км/сек | км/сек |
| Для коэфициента формы р=1/2 | 14,65 | 16,80 | 27,70 | - | - | - |
| Для коэфициента формы р=1/3 | 13,15 | 13,95 | 16,75 | 21,90 | - | - |
| Для коэфициента формы р=1/6 | 12,05 | 12,40 | 13,15 | 14,10 | 16,85 | 27,50 |
| Для коэфициента формы р=1/12 | 11,55 | 11,57 | 12,06 | 12,55 | 13,15 | 14,65 |
| Для калибра 30 см скорость вылета | - | 1 060,35 | 706,90 | 353,45 | - | - |
Кинетическая энергия в момент
вылета для р=1/6 в тоннометрах на 1 см2 | - | 8 309 400 | 6 230 700 | 5 120 400 | | |
Отсюда мы видим, что, например, при технически вполне осуществимой поперечной нагрузке в 1 кг/см2, скорости при вылете из канала ствола в 13 150 м/сек (вместо 11 182 м/сек в безвоздушном пространстве) было бы достаточно для того, чтобы снаряд с коэфициентом формы р = 1/6 добросить до Луны. Достижение этой скорости зависит только от поперечной нагрузки и от коэфициента формы, но не от калибра. Весь вопрос сводится к тому, возможно ли сообщить снаряду эту скорость при вылете его из канала ствола. Ответ на этот вопрос может дать только расчет.
Произвести теоретический расчет нужной для поставленной цели пушки, правда, очень легко. Исходя из величины кинетической энергии снаряда в момент вылета его из канала ствола, равной 8 646 500 кгм/см2, и принимая среднее давление пороховых газов в 6 000 ат, мы получаем необходимую длину ствола в 1 441 м. Желая ограничиться указанной Жюлем Верном в его романе длиной ствола в 216 м, мы должны были бы использовать давление пороховых газов ровно в 40 000 ат. Принимая в соответствии с опытом, полученным при постройке дальнобойных орудий, что наивысшие скорости вылета снаряда из канала ствола получаются при длине ствола в 150 калибров, мы приходим к выводу, что для пушки, способной послать снаряд на Луну, был бы достаточен калибр в 144 см. Если бы при особенно гладком стволе мы могли бы довести его длину до 208 калибров, то для поставленной цели был бы достаточен калибр ровно в 1 м. Однако на практике все эти расчеты остаются совершенно бесполезными, вследствие того, что столь высокое среднее давление не может быть ни достигнуто с помощью современных взрывчатых веществ, ни выдержано нашими лучшими сортами стали, пригодными для изготовления ствола.
Таким образом мы видим, что результат получается отрицательный. Иными словами, с помощью наших современных технических средств возможность посылки снаряда из пушки на Луну совершенно исключена. Однако об этом и не приходится особенно жалеть, потому что, если это и было бы возможно, то в таком снаряде люди никогда не смогли бы предпринять путешествие к нашему спутнику, как это описывает Жюль Верн. Это объясняется тем, что ускорение в момент выстрела должно было бы превысить 300 000 м/сек2. Эта величина примерно в 1 000 раз превосходит то ускорение, которое в лучшем случае может вынести человек без риска быть им мгновенно раздавленным. А послать в мировое пространство с затратой нескольких миллионов рублей артиллерийский снаряд без пассажиров имело бы мало смысла. В самом деле, какая польза была бы в увеличении миллиардных чисел реющих в пространстве железоникелевых метеоров на один стальной снаряд?



