Ниже нами приводится теория полета, взлета и спуска ракеты изложенная К. Циолковским в его следующих сочинениях:
1. „Исследования мировых пространств реактивными приборами". Напечатано в журнале „Научное Обозрение" 1903 г., № 5, стр. 44.
2. „Реактивный прибор как средство полета в пустоте и в атмосфере". Напечатано в журнале „Воздухоплаватель" 1910 г., стр. 110.
3. „Исследование мировых пространств реактивными приборами". (Реактивный прибор „Ракета" К. Циолковского). Напечатано в журнале „Вестник Воздухоплавания" 1911 г., №№ 19, 20, 21, 22.
4. Продолжение той же статьи в том же журнале за 1912 г., №№ 2, 3, 5, 6-7, 9,
5. „Исследование мировых пространств реактивными приборами". Дополнение к I и II частям труда того же названия. Калуга. 1914 г.
6. „Вне земли". Повесть. Калуга 1920 г.
7. „Ракета в космическое пространство". Калуга. 1924 г. (Повторение № 1 с небольшими дополнениями).
8. „Исследование мировых пространств реактивными приборами". Калуга. 1926 г.
Из этого списка сочинений видно, что К. Циолковский впервые опубликовал свою теорию полета ракеты в 1903 году.
В дальнейшем, во избежание повторений названий сочинений, мы при ссылках на них будем указывать дроби, числитель которых выражает номер вышеприведенных названий книг (от 1 до 8), а знаменатель — страницу.
Представим себе в свободном от тяжести пространстве два шарика и между ними упирающуюся в них сжатую пружину. Если пружине дадим возможность расширяться, то одному шарику она сообщит движение направо, другому — налево. При этом она разделит свою работу поровну между обоими шариками. То же будет, если два резиновых мячика будут прижаты друг к другу, а потом отпущены. Тут даже пружина излишня... Или вообразим трубку со сжатым газом. Если один конец ее будет открыт, то газ будет давить только на другой конец, и труба, под влиянием этого давления, кинется, положим, направо. Тогда газ устремится налево. То же будет с ружьем и пушке при выстреле.
Окружающая приборы материальная среда или атмосфера играет роль второстепенную и, может-быть, даже мешает проявлению реакции во всей чистоте и силе.
Ниже мы излагаем теорию движения ракеты, опубликованную им в 1903 году по сочинениям №№ 1—8.
Обозначения:
M1 — масса снаряда со всем содержимым, кроме запаса взрывчатых веществ.
М2 — полная масса взрывчатых веществ.
М — переменная масса взрывчатых веществ, оставшихся не взорванными в снаряде в данный момент.
V1 — скорость взрывающихся элементов относительно ракеты.
dМ—бесконечно-малый отбросок взрывчатого вещества, вырывающегося из раструба с постоянной скоростью V1.
V - переменная скорость движения ракеты.
dV - приращение скорости ракеты.
Полная масса ракеты в начале взрыва будет M1+M2.
Во время взрывов она будет переменной М1+ М.
В конце взрывов она будет постоянной М1.
Чтобы ракета получила наибольшую скорость, необходимо, чтобы отбрасывание продуктов взрыва совершалось в одном направлении относительно звезд. А для этого нужно, чтобы ракета не вращалась, а чтобы она не вращалась, надо чтобы равнодействующая взрывающих сил, проходящая через центр их давления, проходила в то же время и через центр инерции всей совокупности летящих масс.
Итак, предполагая такое наивыгоднейшее отбрасывание газов в одном направлении, получим следующее дифференциальное уравнение, на основании закона о постоянстве количества движения:
Разделяя переменные и интегрируя, получим:
М=М2 и V=0;
Поэтому уравнение 3 получает вид:
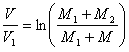 . . . . . . (5)
. . . . . . (5)Наибольшая скорость снаряда получится, когда весь запас взрывчатого вещества будет взорван, т. е. когда М=0.
Тогда:
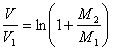 . . . . . . (6)
. . . . . . (6)Из уравнения (6) видно, что скорость V снаряда возрастает неограниченно с возрастанием количества М2 взрывчатых веществ, при чем однако V возрастает все медленнее и медленнее.
В качестве взрывчатого вещества Циолковский принимает смесь водорода с кислородом, которые, соединяясь в газообразном состоянии для образования одного кг воды, развивают 3825 калорий (калория — количество тепла для нагревания 1 кг воды на 1°С), что дает работу 3 825 · 424 = 1 621 800 кгм. Предполагая силу тяжести постоянной, получим, что эта работа соответствует работе 1 кг массы, движущейся со скоростью, определяемой из уравнения
Подставляя это значение в формулу (6), мы можем вычислить величину скорости снаряда в зависимости от отношения ![]() . Однако возрастание скорости ракеты сопровождается несравненно быстрейшим возрастанием массы М2 взрывчатых веществ. Поэтому, насколько легко и возможно увеличение массы поднимающегося в небесное пространство снаряда, настолько затруднительно увеличение его скорости.
. Однако возрастание скорости ракеты сопровождается несравненно быстрейшим возрастанием массы М2 взрывчатых веществ. Поэтому, насколько легко и возможно увеличение массы поднимающегося в небесное пространство снаряда, настолько затруднительно увеличение его скорости.
Результаты подсчетов по формуле (6) приведены в следующей таблице 1.
| V м/сек | V м/сек | ||||
| 0,1 0,2 0,3 0,4 0,5 1 2 3 4 5 6 |
0,095 0,182 0,262 0,336 0,405 0,693 1,098 1,386 1,609 1,792 1,946 |
543 1037 1493 1915 2308 3920 6260 7880 9170 10100 11100 |
7 8 9 10 19 20 30 50 100 193
беско
| 2,079 2,197 2,303 2,398 2,996 3,044 3,434 3,932 4,612 5,268 нечно |
11800 12500 13100 13650 17100 17330 19560 22400 26280 30030 бесконечно |
Из таблицы видно, что скорости V получаются весьма значительными, например, при ![]() = 193, V = 30 030 м/сек, т. е. почти равна скорости движения земли по своей орбите. Когда
= 193, V = 30 030 м/сек, т. е. почти равна скорости движения земли по своей орбите. Когда ![]() = 1, то V получается почти вдвое больше той, которая необходима для отлета с луны и достаточной для удаления с Марса или Меркурия. При
= 1, то V получается почти вдвое больше той, которая необходима для отлета с луны и достаточной для удаления с Марса или Меркурия. При ![]() =3, скорость будет почти равна той, которая необходима для превращения снаряда в спутника земли.
=3, скорость будет почти равна той, которая необходима для превращения снаряда в спутника земли.
При ![]() = 6, скорость достаточна для удаления снаряда от земли и вращения его вокруг солнца в качестве самостоятельной планеты и т. д.
= 6, скорость достаточна для удаления снаряда от земли и вращения его вокруг солнца в качестве самостоятельной планеты и т. д.
При меньших отношениях ![]() снаряд все же может подняться высоко над землей. Например, при
снаряд все же может подняться высоко над землей. Например, при ![]() = 0,1, и при V = 543 м/сек высота подъема будет около 15 км.
= 0,1, и при V = 543 м/сек высота подъема будет около 15 км.
Из таблицы видно, что при незначительном запасе, скорость, по окончании взрыва, приблизительно, пропорциональна массе запаса (М2), следовательно, в этом случае, высота поднятия пропорциональна квадрату этой массы (М2) запаса.
Утилизацией ракеты назовем отношение работы ракеты к работе взрывчатого материала. Определим эту утилизацию. Работа взрывчатых вешеств равна:
Работа ракеты равна:
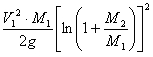
Поэтому утилизация будет равна:
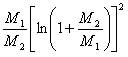 . . . . . . (7)
. . . . . . (7)В нижеследующей таблице II подведены результаты подсчетов при разных ![]() . Из таблицы и из формулы (7) видно, что при очень малых количествах взрывчатого вещества утилизация его равна
. Из таблицы и из формулы (7) видно, что при очень малых количествах взрывчатого вещества утилизация его равна ![]() т. е. тем меньше, чем относительное количество взрывчатых веществ меньше.
т. е. тем меньше, чем относительное количество взрывчатых веществ меньше.
Это следует из следующего:
следовательно, приблизительно:
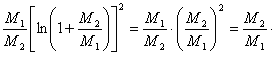
| Утилизация | Утилизация | ||
| 0,1 0,2 0,3 0,4 0,5 1 2 3 4 5 6 |
0,090 0,165 0,223 0,282 0,328 0,48 0,60 0,64 0,65 0,64 0,63 |
7 8 9 10 19 20 30 50 100 193 бесконечно |
0,62 0,60 0,59 0,58 0,47 0,46 0,39 0,31 0,21 0,144 нуль |
Далее, с увеличением ![]() утилизация возрастает, достигая максимума при
утилизация возрастает, достигая максимума при ![]() = 0,65, а затем убывает. Вообще при
= 0,65, а затем убывает. Вообще при ![]() = 1 до 20 утилизация довольно велика и равна около 0,5.
= 1 до 20 утилизация довольно велика и равна около 0,5.
Мы видели, что без влияния тяжести ракета может приобрести большую скорость. Эту же скорость она может получить и для среды тяжести, если только взрыв будет мгновенный. Но такой взрыв для нас не годится, потому что происходящего во время его толчка не выдержат ни люди, ни вещи, заключенные в снаряде. Нам нужно медленное взрывание. Однако, при очень медленном взрывании полезный эффект уменьшается и даже может обратиться в нуль, когда постоянное ускорение р ракеты будет равно ускорению силы тяжести g земли, и снаряд во все время взрывания будет стоять в воздухе неподвижно без опоры.
Если ракета движется в среде, свободной от тяжести, то время t, в течение которого взрывается весь запас взрывчатого вещества, равно
В этом случае количество взрывчатых веществ, расходуемых на единицу времени, непрерывно уменьшается пропорционально уменьшению массы снаряда с остатком невзорванных материалов. Зная р или ускорение в среде без тяжести, можно вычислить и величину (временную) тяжести внутри ракеты в течение ее ускоряющегося движения.
Приняв силу тяжести у поверхности земли за единицу, найдем величину временной тяжести в снаряде ![]() , которая показывает увеличение давления вещей на подставки. Обозначим скорость ракеты по окончании взрывов в среде тяжести с постоянным ускорением g через V2.
, которая показывает увеличение давления вещей на подставки. Обозначим скорость ракеты по окончании взрывов в среде тяжести с постоянным ускорением g через V2.
Тогда время, в течение которого расходуется один и тот же запас взрывчатого материала, будет то же, как и без влияния тяготения, именно:
Если p = 0, то и ![]() =0. Это соответствует отсутствию взрывов. При этом, снаряд будет двигаться по инерции, и внутри него не будет веса, т. е. его нельзя будет обнаружить при помощи пружинных весов.
=0. Это соответствует отсутствию взрывов. При этом, снаряд будет двигаться по инерции, и внутри него не будет веса, т. е. его нельзя будет обнаружить при помощи пружинных весов.
Если р = g, то ![]() =1. Этот случай имеет место, когда силою взрывов ракета неподвижно висит над землей. Относительная тяжесть равна земной. Если до взрыва снаряд имел уже какую-нибудь скорость, например вверх, вбок и т. п., то она останется без изменения. Из формул (8) и (9) имеем:
=1. Этот случай имеет место, когда силою взрывов ракета неподвижно висит над землей. Относительная тяжесть равна земной. Если до взрыва снаряд имел уже какую-нибудь скорость, например вверх, вбок и т. п., то она останется без изменения. Из формул (8) и (9) имеем:
Формулы (10) и (11) показывают, что тяготение уменьшает скорость ракеты, и последняя даже равна нулю, если ![]() =1. Чем больше будет
=1. Чем больше будет ![]() , тем больше будет и скорость ракеты. Однако увеличение не может быть беспредельно, так как это грозит опасностью пассажирам.
, тем больше будет и скорость ракеты. Однако увеличение не может быть беспредельно, так как это грозит опасностью пассажирам.
В пределе, когда ![]() бесконечно велико, мы получаем формулу (11) формулу (6):
бесконечно велико, мы получаем формулу (11) формулу (6):
По формуле (9) определяется время взрывания, например:
1) При К = 11 100 м; ![]() = 6; t = 1133 сек. = 19 мин., т. е. в среде, свободной от тяжести, ракета пролетала бы равномерно ускоряющимся движением в 19 минут или в среде тяжести простояла бы неподвижно у поверхности земли в течение тех же 19 минут.
= 6; t = 1133 сек. = 19 мин., т. е. в среде, свободной от тяжести, ракета пролетала бы равномерно ускоряющимся движением в 19 минут или в среде тяжести простояла бы неподвижно у поверхности земли в течение тех же 19 минут.
2) При V = 3920 м; ![]() = 1; t = 400 сек. = 6 ⅔ м.
= 1; t = 400 сек. = 6 ⅔ м.
3) При V = 543 м ![]() = 0,1; t = 55,4 сек.
= 0,1; t = 55,4 сек.
Таким образом взрывание будет безрезультатным, если оно происходит недостаточно сильно, хотя и долго. Оно тогда годится лишь для продвижения по поверхности земли, хотя и короткое время, но зато во время его будет пройдено большое расстояние. (Возможен случай полета и над атмосферой).
Чем меньше g, тем дольше ракета простоит в среде тяготения. Например, на луне при ![]() = 6, t = 2 часам.
= 6, t = 2 часам.
Если ускорение будет в 10 раз больше нормального, т. е. ![]() = 10, то при
= 10, то при ![]() = 6 получим V2 = 9 990 м и по формуле (8) найдем t = 113 сек.
= 6 получим V2 = 9 990 м и по формуле (8) найдем t = 113 сек.
Сравним теперь работу взрывчатых веществ при полете ракеты в среде без тяготения и в среде с тяготением.
В среде тяжести ускорение будет р1 = р - g. Предположим, что до высоты нескольких сот км g постоянно. Тогда высота поднятия ракеты за время взрывания t будет:
Подставляя вместо V2 его значение по (10), получим
Полезная работа ракеты в среде, свободной от тяготения, будет:
Работа же в среде тяготения:
Отношение этих работ будет:
Исключая из этой формулы h и V2 получим:
Например, для вышеразобранного случая (![]() = h;
= h; ![]() =10) имеем потерю
=10) имеем потерю ![]() и утилизацию 0,9. Когда p=g и снаряд стоит в воздухе, потеря будет полная и утилизация = 0. Такова же будет утилизация, если снаряд будет иметь постоянную горизонтальную скорость.
и утилизацию 0,9. Когда p=g и снаряд стоит в воздухе, потеря будет полная и утилизация = 0. Такова же будет утилизация, если снаряд будет иметь постоянную горизонтальную скорость.
Для вышеупомянутого случая (![]() = h;
= h; ![]() =10), высота подъема h = 565 км.
=10), высота подъема h = 565 км.
Скорость V2 будет также меньше V, что следует из формулы (10)
Эта формула имеет тот же вид, что и (18).
Из формулы (18) имеем:
Если известно Т1, то по ней вычисляем Т и далее V для среды без тяжести по формуле
Зная V, определяем М2 — массу взрывчатых веществ — по формуле (5) и получим
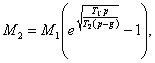 . . . . . . (20)
. . . . . . (20)Здесь под g следует подразумевать постоянное сопротивление, равное сумме сил тяжести и сопротивления среды. Но сила тяготения постепеннo убывает с удалением от центра земли, вследствие чего утилизируется большее количество работы взрывчатых веществ. С другой стороны, сопротивление атмосферы, будучи, как увидим, весьма незначительным по сравнению с тяжестью снаряда, уменьшает утилизацию ракеты.
Однако последняя убыль с избытком вознаграждается прибылью от уменьшения притяжения. Поэтому формулу (20) можно применять к вертикальному поднятию ракеты.
Пусть ракета силою взрыва некоторого (не всего) количества газов приобрела в среде без тяготения скорость 10 100 м/сек (табл. I). Для остановки ее ей необходимо приобрести такую же скорость, но в обратном направлении.
Согласно таблице I количество оставшихся взрывчатых веществ должно быть в 5 раз больше массы М1 ракеты. Поэтому она, по окончании первой части взрыва, должна иметь запас взрывчатого вещества М2 — 5M1 и полную массу 6М1. Этой массе первоначальное взрывание должно было сообщить скорость 10 000 м/сек, для чего необходимо было иметь взрывчатого вещества 6 М1 × 5 = 30 М1, что вместе с запасом 5 M1 составляет 35 M1.
Обозначим ![]() = q, и через M3 — полную массу взрывчатого вещества, необходимую для взлета и остановки (в нашем случае M3 = 35 M1).
= q, и через M3 — полную массу взрывчатого вещества, необходимую для взлета и остановки (в нашем случае M3 = 35 M1).
Тогда
Всего же, с массою ракеты М1=1:
На основании формулы (22) и таблицы I составляем таблицу III. Эта таблица показывает, что если мы хотим приобрести очень большую скорость и затем потерять ее, то необходим весьма (неодолимо) большой запас взрывчатых веществ.
| V м | V м | ||||
| 543 1037 1493 1915 2308 3920 6260 7880 9170 10100 11100 |
0,1 0,2 0,3 0,4 0,5 1 2 3 4 5 6 |
0,21 0,44 0,69 0,96 1,25 3 8 15 24 35 48 |
11800 12500 13100 13650 17100 17330 19560 22400 26280 30038 бесконечно |
7 8 9 10 19 20 30 50 100 193 бесконечно |
63 80 99 120 399 440 960 2600 10200 37248 бесконечно |
Заметим, что из формул (22 bis) и (6) можно также получить данные таблицы III.
В среде тяготения процесс работы взрывчатых веществ будет одинаков как при поднятии ракеты с земли на некоторую высоту, когда взрывчатые вещества сообщали ей скорость поднятия до остановки, так и при падении ее с этого места до земли, когда они тормозили ее спуск.
Остановка в среде тяготения требует большей работы взрывчатых веществ, чем в среде без тяготения, и поэтому в формулах (21) и (22) q будет больше.
Обозначим это большое отношение через q1, тогда будем иметь:
Так как работы взрывчатых веществ пропорциональны их массам, то
Подставляя это выражение в (22), получим:
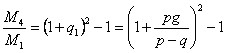 . . . . . . (24)
. . . . . . (24)Здесь M4 означает количество взрывчатых веществ, необходимых для поднятия с известной точки и возвращения в ту же точку при полной остановке ракеты и при полете ее в среде тяжести.
Составим таблицу IV, полагая ![]() = 10.
= 10.
| 0,1 0,3 0,5 1,0 2 |
0,235 0,778 1,420 4,457 9,383 |
3 4 5 6 7 |
17,78 28,64 41,98 57,78 76,05 |
Хотя вертикальное движение ракеты как-будто выгоднее, потому что при этом скорее рассекается атмосфера и ракета поднимается на большую высоту, но, с одной стороны, работа для прохода атмосферы, сравнительно с полною работой взрывчатых веществ, весьма незначительна, с другой, при наклонном движении, можно устроить постоянную обсерваторию, движущуюся за пределами атмосферы неопределенно долгое время вокруг земли, подобно ее луне. Кроме того, и это главное, при наклонном полете утилизируется несравненно большая часть энергии взрыва, чем при вертикальном движении.
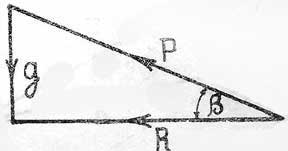 Черт. 32. |
Рассмотрим сначала горизонтальный полет ракеты.
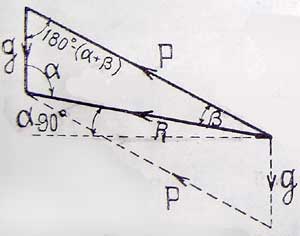
При таком полете ракета находится под влиянием двух сил: 1) тяжести и 2) отдачи. Их равнодействующая должна быть горизонтальной. Обозначим через R -- горизонтальное ускорение, через р - ускорение от взрывов и через g -- ускорение от силы тяжести (черт. 32). Тогда будем иметь:
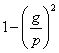 . . . . . . (28)
. . . . . . (28)В таблице V приведены эти потери при разных p : g, при чем вычислены и соответствующие углы между направлениями р и R.
| Потеря | sin β | β° | |
| 1 2 3 4 5 10 100 |
1 1:4 1:9 1:16 1:25 1:100 1:10000 |
1 1:2 1:3 1:4 1:5 1:10 1:100 |
90 30° 19,5 14,5 11,5 5,7 0,57 |
 Черт. 33 |
Горизонтальный полет ракеты невыгоден потому, что при этом сильно увеличивается его путь через атмосферу и тратится работа на рассечение воздуха. Назовем через α угол наклона траектории R полета к вертикали. (Черт. 33). Этот угол > 90°. Из чертежа имеем:
Кинетическая энергия выражается формулой (26), но в ней R определяется по формуле (29).
Вертикальное ускорение равно:
Работа поднятия ракеты будет:
Здесь за единицу работы принято поднятие ракеты на единицу высоты с ускорением g.
Работа в среде, свободной от тяжести, будет (по 27):
Утилизацию энергии взрывчатых веществ при полете в среде тяготения по сравнению с таковой же в среде без тяготения, получим, разделив (32) на (27):
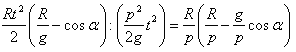 . . . . . . (33)
. . . . . . (33)Выключая отсюда R по формуле (29), найдем:
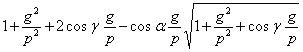 . . . . . . (34)
. . . . . . (34)Формулы (18) и (28) представляют частные случаи этой формулы.
Пример. Пусть ракета летит под углом 14,5° к горизонту. Синус этого угла составляет 0,25; это значит, что сопротивление атмосферы увеличивается в 4 раза сравнительно с сопротивлением ее при отвесном полете, так как оно приблизительно пропорционально синусу угла наклона α-90° траектории ракеты к горизонту.
Имеем:
По формуле (34) определяем утилизацию 0,966. Потеря составляет 0,034 или около 3,4%. Эта потеря в 3 раза меньше, чем при вертикальном движении. Результат не дурной, если принять во внимание, что сопротивление атмосферы и при наклонном движении (14½°), никак не более 1% работы удаления снаряда от земли.
В таблице VI показаны утилизации и потери при разных наклонах траектории ракеты к горизонту. 1-й столбец показывает наклон движения к горизонту (черт. 33).
β - есть угол между направлением взрыва и траекторией.
| α-90° | α | β | α+β | Утилизация | Потеря |
| 0 2 5 10 15 20 30 40 45 90 |
90 92 95 100 105 110 120 130 135 180 |
5¾ 5⅔ 5⅔ 5⅔ 5½ 5⅓ 5 4⅓ 4 0 |
95¾ 97⅔ 100⅔ 105⅔ 110 ½ 115 ⅓ 125 134 ⅓ 139 180 |
0,9900 0,9860 0,9800 0,9731 0,9651 0,9573 0,9426 0,9300 0,9246 0,9000 |
1:100 1:72 1:53 1:37 1:29 1:23,4 1:17,4 1:14,3 1:13,3 1:10 |
Для очень малых углов наклона α-90° формулу (34) можно упростить, заменив тригонометрические величины дугами и сделав другие упрощения.
Тогда получим следующее выражение для потери работы
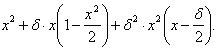
Здесь δ — означает угол наклона движения (α — 90°), выраженный длиною его дуги при радиусе=1, а х = ![]() . Отбрасывая малые величины высших порядков, получим:
. Отбрасывая малые величины высших порядков, получим:
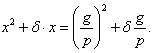
Положим δ — 0,02 N, где 0,02 есть часть окружности, соответствующая почти одному градусу (11/7°), a N — число этих градусов. Тогда потеря работы выразится:
Положив, например, как и раньше ![]() =0,1, составим таблицу VII, из которой видно, что несходимость результатов до углов < 10° по сравнению с таблицей VI не велика.
=0,1, составим таблицу VII, из которой видно, что несходимость результатов до углов < 10° по сравнению с таблицей VI не велика.
| N° | Потеря | N° | Потеря |
| 0 0,5 1 2 3 |
1:100 1:91 1:83 1:70 1:60 |
4 5 6 10 |
1:55 1:50 1:45 1:33 |
Взлет с земли. В своем сочинении „Вне земли“ (стр. 18) Циолковский описывает взлет ракеты следующим образом: „Ракета сначала летит параллельно плоскости экватора под ∠ 25° к горизонту по направлению вращения земли, в течение первых 10 секунд ее скорость возрастает быстро до 500 метров; затем, во все время пути через атмосферу, увеличивается гораздо медленнее, по мере ее разряжения. После прохождения воздушной оболочки земли, скорость опять должна быстро возрастать, а направление движения постепенно изменяется и на высоте 1000 километров сделается кругообразным, при чем скорость должна быть настолько велика, чтобы ракета двигалась кругом земного шара по окружности, не приближаясь к нему. Облет вокруг земли производится при скорости 7 ½ км в сек.
На стр. 23 он описывает впечатления зрителей, оставшихся на земле и наблюдавших взлет ракеты. „Они видели, как ракета сорвалась и устремилась в наклонном положении в пространство. Многие в испуге отшатнулись. Всех оглушил шум, но он быстро утихал, по мере удаления ракеты. Она быстро удалялась к востоку, по направлению движения земли вокруг оси. В то же время она поднималась все выше и выше, через 10 сек. она была от зрителей на расстоянии 5 километров и двигалась со скоростью 1 000 м/сек. (выше было указано 500?). Она уже едва была видна в сильный бинокль и то потому, что от воздушного трения стала светиться. Можно сказать, что она исчезла почти моментально из глаз зрителей. Послышался как бы громовой рокот. Он сначала возрастал, потом стал ослабевать. Громовые раскаты продолжались, хотя ракеты уже не было видно. Толпа смотрела по сторонам, но туч нигде не было: эта ракета раздвинула воздух, который и дал громоподобную воздушную волну.
Взлет с луны. Циолковский описывает следующим образом („Вне земли“, стр. 91 и 92). Выбрали ровное место, — часть горы, поднимающейся под уклоном 10 — 20 градусов. На ней поставили ракету, заперлись в ней и привели в действие взрывные аппараты. Сначала они катились по горе, потом оставили ее и помчались в эфирном пространстве, кругом луны. Они поднимались все выше и выше, приобретали скорость все больше и больше, пока не достигли секундной скорости в 1600 метров. Тогда взрывание было прекращено. Они мчались кругом луны на расстоянии 265 километров от ее поверхности.
Покружившись несколько часов кругом луны, они снова возобновили взрывание, достигли скорости около 2 ½ км в сек., прекратили взрывание и помчались от луны на земную орбиту.
Взлет с астероида можно произвести незначительными взрываниями тем меньшими, чем меньше его масса.
Спуск на землю. После экскурсии к внешним планетам ракета Циолковского возвращается обратно к земле („Вне земли“, стр. 111), описывая вокруг солнцa спиральный путь и приближаясь постепенно к земной орбите. Когда ракета была от этой орбиты на 65 миллионов километров, было начато торможение при скорости движения в 25 км/сек. Однако, притяжение солнца эту скорость увеличивало и при вступлении ракеты на орбиту земли скорость сравнялась с земной. Начало сказываться притяжение земли. Пришлось тормозить движение обратными взрывами. Когда земля была уже близко, люди погрузились в резервуары с водой. Спуск же ракеты регулировался приборами, также погруженными в жидкость. Ракета вступает в атмосферу, накаливается тонкая предохранительная оболочка, но скорость ее уже не велика и еще умоляется, по мере приближения к поверхности океана. Еще энергичное торможение и ракета почти остановилась. Легкий шлепок в воду и она плавает на ней, как миноноска.
Спуск на луну происходил следующим образом. Под влиянием лунного притяжения ракета с лунной орбиты стала направляться к луне пока относительная скорость ее не стала равна 2 км/сек. Когда расстояние до луны было 2 000 км, начали взрыванием тормозить движение, пока ракета не остановилась в расстоянии 3 км над луной. Затем ей сообщили движение 100 м/сек по направлению к луне. Когда осталось 500 м, опять затормозили и, наконец, ракета с едва заметным толчком опустилась на почву, повернулась, оперлась на колеса, прокатилась несколько десятков метров по долине и остановилась („Вне земли“, стр. 88).
Спуск на астероид („Вне земли“, стр. 103). Когда был замечен астероид, то взрыванием ракету направили к нему. При достаточном приближении замедлили скорость контр-взрывами и постепенными взрывами привели ракету в расстояние нескольких десятков метров от астероида, при чем ракета расположилась в относительном покое. Под влиянием притяжения и контр-взрывов наконец ракета пристала к планете.
Мы могли бы рассмотреть еще очень многое: работу тяготения, сопротивление атмосферы, о пребывании человека в среде лишенной кислорода, о направлении ракеты при проходе ее к атмосфере, о пути ракеты в космическом пространстве.
Выше была изложена теория, данная Циолковским в 1903 году. Продолжение ее было напечатано в 1911 —12 гг., каковое мы теперь и излагаем (см. „Вестн. Воздух.“ 1911 и 12 гг.)
При удалении единицы массы от поверхности планеты радиуса r1 на высоту h необходимо затратить работу Т:
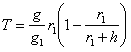 . . . . . . (35)
. . . . . . (35)Здесь g — ускорения силы тяжести на поверхности планеты и g1 — земли.
Если
т. е. работа, необходимая для удаления единицы массы от поверхности планеты на бесконечно-большое расстояние равна работе поднятия той же массы от поверхности на один радиус планеты, если допустить, что сила тяжести при этом не меняется.
Для равноплотных планет сила тяжести у поверхности пропорциональна радиусу планеты и выражается отношением радиуса r1 планеты к радиусу r2 земли:
1Здесь под словом сила следует понимать ускорение.
Это показывает, что предельная работа Т1 быстро уменьшается с уменьшением радиуса r1 планеты.
Для земного шара Т1= 6 366 000 кгм, что меньше энергии 1½ кг нефти.
Для подъема человека весом в 70 кг потребуется, таким образом, около 70 кг нефти.
Для лун Марса (диаметр 10 км) Т1= 16 кгм.
Для луны ![]() .
.
Для планетоида Весты ![]() . (Диаметр 500 км).
. (Диаметр 500 км).
Для всякой планеты | 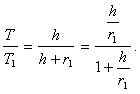 |
Вычислим по этой формуле таблицу VIII.
| Поднятие в радиусах планеты Отношение соответствующей работы к работе для удаления в бесконечность | 1 |
2 |
3 |
9 |
99 |
Бесконечно 1 |
Скорость V1, необходимая для поднятия ракеты на высоту К и получения после этого скорости V, равна:
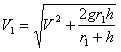 . . . . . . (37)
. . . . . . (37)Если V =0, т. е. тело движется до остановки его силою тяжести, то:
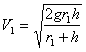 . . . . . . (38)
. . . . . . (38)Если h = ∞, то
Например, для земли V1 = 11 170 м/сек.
![]() луны V1 = 2373
луны V1 = 2373![]()
![]() планетоида
планетоида
![]() Агаты (D = 6⅓ км) V1 = 5,7 м/ceк.
Агаты (D = 6⅓ км) V1 = 5,7 м/ceк.
Для планет, равноплотных с землей
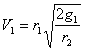 . . . . . . (40)
. . . . . . (40)Для Весты (D= 400 км) V1 = 324 м/сек.
Вечное кружение вокруг планеты требует работы вдвое меньшей и скорости в ![]() =1,41 раз меньшей, чем для удаления от планеты.
=1,41 раз меньшей, чем для удаления от планеты.
Время t падения неподвижного сначала тела на планету или солнце, масса которого сосредоточена в одной точке, равно:
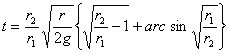 . . . . . . (41)
. . . . . . (41)Та же формула выражает и время поднятия с r2 — r до r2 когда тело теряет свою скорость.
Если r = r2, то
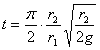 . . . . . . (42)
. . . . . . (42)Хотя здесь t выражает время падения до центра массы планеты, но при обыкновенных условиях по этой же формуле можно приблизительно определить и время падения до поверхности планеты или поднятия с нее до остановки.
С другой стороны, время полного кругового обращения какого-нибудь тела вокруг планеты равно:
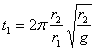
r1 — радиус планеты с ускорением g,
r2 — расстояние тела от ее центра.
Сравнивая (42) и (43), найдем:
Например, луна упала бы на землю в 4,8 суток.
„ земля![]() солнце „ 4¼
солнце „ 4¼![]()
Наоборот, ракета, брошенная с земли и остановившаяся на расстоянии луны, летела бы 4,8 суток.
Определим работу, которую произведет ракета, рассекая атмосферу при прямолинейном равномерно-ускоренном движении. При этом необходимо принять в расчет переменную плотность воздуха на разных высотах.
Циолковский выражает эту плотность d формулой 1)
1) Вывод см. журнал „Воздухоплаватель", 1905 год, № 3, стр. 66.
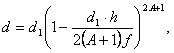 . . . . . . (45)
. . . . . . (45)h — высота положения ракеты,
f — давление воздуха у уровня моря (f=103,33 кг на кв. дм),
М — механический эквивалент тепла (M = 4 240 кг/дм),
С — теплоемкость воздуха при постоянном объеме 0,169,
T1 — температура абсолютного нуля —273°С. Подставляя эти значения, получим А=2,441 и
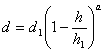 . . . . . . (46)
. . . . . . (46)Диференциал работы сопротивления воздуха равен
S — площадь миделевого сечения ракеты,
d — плотность воздуха в месте нахождения ракеты,
V — скорость ракеты,
g — ускорение силы земной тяжести (9,8), u — коэффициент формы ракеты (принимается постоянным).
Так как сопротивление воздуха по сравнению с давлением на ракету взрывчатых веществ не велико (около 1%) то можно принять:
Это предположение, давая большие значения скорости, увеличит величину работы сопротивления воздуха и, следовательно, уравняет погрешность, допущенную выше, когда мы приняли сокращенную высоту атмосферы 54,54 км.
Из (46), (47), (48) и (49) имеем:
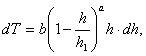 . . . . . . (50)
. . . . . . (50)Интегрируя по частям и определяя постоянное, получим
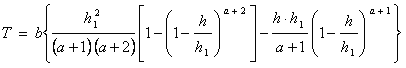 . . . . . . (52)
. . . . . . (52)Полагая h=h1, получим полную работу T1 сопротивления атмосферы:
Положим:
Тогда
Работа 1 т взрывчатых веществ при получении из водорода и кислорода одной т воды, равна 1 600 000 т/м.
Если ракета со всеми приспособлениями и пассажирами весит 1 т, а взрывчатый запас равен ушестеренному количеству, т. е. 6 т, то ракета захватит с собою потенциальную энергию в ![]() работы тяготения. То же можем получить, сравнив прямо работу сопротивления атмосферы (17 975) с полной работой тяготения (6 336 000). Найдем около
работы тяготения. То же можем получить, сравнив прямо работу сопротивления атмосферы (17 975) с полной работой тяготения (6 336 000). Найдем около ![]() .
.
В таблице IX показаны, по принятым условиям, время в секундах от начала вертикального полета, соответствующая секундная скорость ракеты в метрах, высота подъема в метрах и плотность окружающего воздуха, при чем предположено, что плотность у уровня моря равна единице и температура понижается равномерно с высотою на 5°С 2).
| Время подъ- ема ракеты t сек. | Скорость подъема ра- кеты V м/сек. | Высота подъема h м | Относитель- ная плот- ность воз- духа d |
| 0 1 2 3 5 7 10 15 20 30 40 50 70 100 113 |
0 90 180 270 450 630 900 1350 1800 2700 3600 4500 6300 9000 9900 |
0 45 180 405 1125 2205 4500 10125 18000 40500 72000 112500 220500 450000 574000 |
1 - - - 1: 1,13 - 1: 1,653 - 1:10,63 1:2828 близко к нулю 0 0 0 |
Работа сопротивления атмосферы почти в 35 раз меньше потери работы от силы тяжести при вертикальном поднятии. Поэтому выгодно наклонять путь движения ракеты с тем, чтобы, увеличив в несколько раз величину сравнительно малую, т. е. сопротивление воздуха, уменьшить в то же время величину сравнительно большую, т. е. потерю энергии от влияния тяжести. Работу сопротивления атмосферы можно принять, приблизительно, пропорциональной cosec2 (90° — α); (90° — α) есть угол наклонения движения ракеты к горизонту. Это предположение довольно верно до некоторого угла.
| Время подъема t.....сек. Скорость подъема V.....м·сек Высота подъема h......м | 1 20 10 | 2 40 40 | 10 200 1000 | 50 1000 25000 |
100 2000 100000 |
1) В сочинении „Вне земли“ (стр. 4) Циолковский дает таблицу, аналогичную IX и вычисленную для 2) На 1000 м. См. журнал „Воздухоплаватель“ 1905 г. № 3, стр. 65.![]() = 3, именно (табл. IX = bis).
= 3, именно (табл. IX = bis).
| Угол наклона траектории к горизонту 90°-α | Sin 90°-α | cosec 90°-α | Потери энергии | |||
| От тяжести (см. табл. VI) | cosec2 90°-α | От атмо- сферы U=100 | От тяжести и атмосферы | |||
| 0 2 5 10 15 20 30 40 45 90 |
0 0,0349 0,0872 0,174 0,259 0,342 0,500 0,643 0,707 1,000 |
∞ 28,7 11,5 5,75 3,86 2,92 2,00 1,56 1,41 1,00 |
0,010 0,014 0,020 0,027 0,035 0,045 0,057 0,070 0,075 0,100 |
∞ 824 132 33,1 14,9 8,53 4,00 2,43 1,99 1,00 |
∞ 2,47 0,395 0,099 0,0477 0,0255 0,0120 0,0073 0,0059 0,0030 |
- 2,48 0,415 0,126 0,0827 0,0705 0,069 0,0773 0,0809 0,1030 |
В таблице X приведены: 1) углы наклона полета к горизонту, потери работы от тяжести и от сопротивления атмосферы (U=100) и суммы этих потерь.
При U =100 min потерь будет будет при 90°-α 10-15°.
Потери составляют 0,07 всей энергии нарывчатых веществ в среде без тяжести или около 7%.
В среде без тяжести, при ушестеренном количестве взрывчатых веществ, сравнительно с весом всего остального, утилизируется 0,63 всей их скрытой энергии. Отбросив на упомянутые потери 7% этого числа, найдем, что при наклонном движении можно использовать 59% всей химической энергии взрывчатого вещества.
Работу сопротивления воздуха можно уменьшить в несколько раз, если начать полет с вершины высочайших гор, или, подняв ракету с помощью воздушного корабля на значительную высоту, начать полет оттуда.
Так, полет с высоты 5 км уменьшает работу сопротивления вдвое, а с 10 км — вчетверо.
В зависимости от направления и места взлета, от величины и направления начальной скорости и от запаса горючего (отношение массы взрывчатых веществ к остальной массе ракеты ![]() ), траектория полета ракеты будет изменять свой вид и будут меняться результаты полета. На чертежах 34 — 35 и в таблице XI приведены различные случаи полета, при чем как чертежи, так и таблицы составлены нами на основании указании Циолковского, приведенных в вышеупомянутом журнале. №№ траекторий соответствуют строкам таблицы (в статье Циолковского чертежей и таблицы нет).
), траектория полета ракеты будет изменять свой вид и будут меняться результаты полета. На чертежах 34 — 35 и в таблице XI приведены различные случаи полета, при чем как чертежи, так и таблицы составлены нами на основании указании Циолковского, приведенных в вышеупомянутом журнале. №№ траекторий соответствуют строкам таблицы (в статье Циолковского чертежей и таблицы нет).
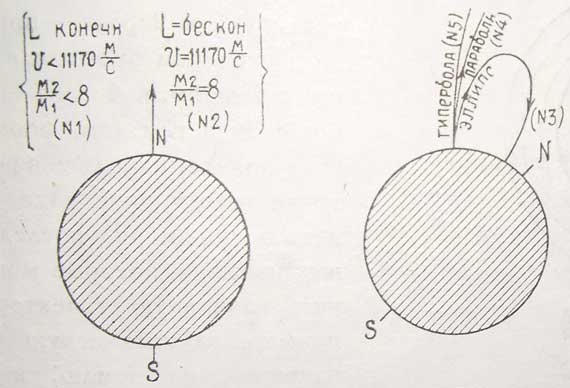
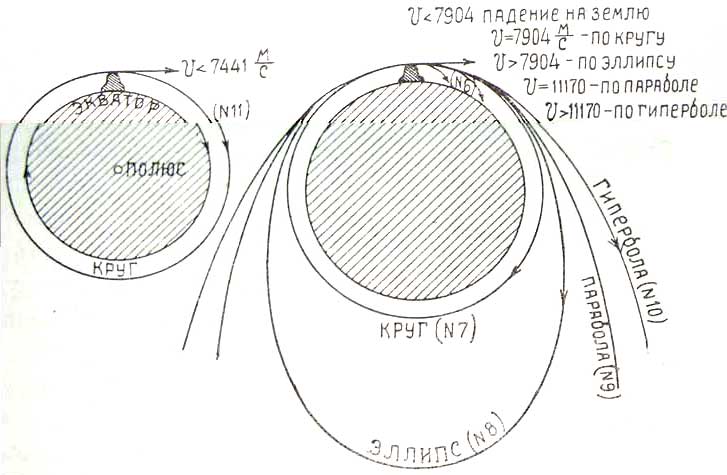
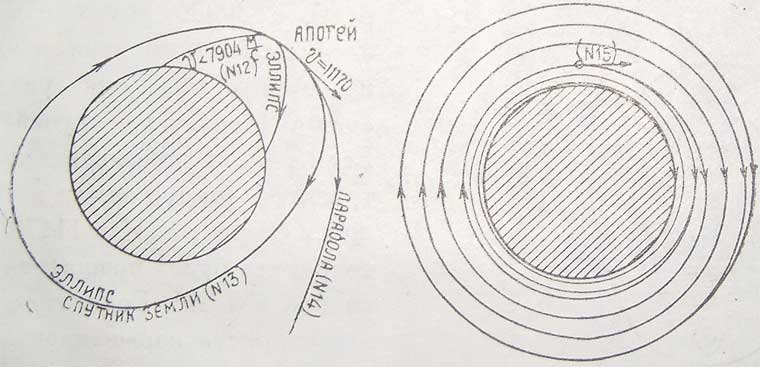
При расчете траекторий сопротивление атмосферы во внимание не принималось. Если учитывать его, то ракете необходимо придавать скорости больше показанных в таблице XI и на чертежах, в противном случае ракета будет или падать на землю или двигаться по иной кривой. Заметим, что в таблице показаны в отношениях ![]() массы взрывчатых веществ М2, лишь необходимых для взлета ракеты.
массы взрывчатых веществ М2, лишь необходимых для взлета ракеты.
Для безопасного же обратного падения эта масса должна быть увеличена в 2 раза — при небольшом удалении от земли, в 3 раза при большом, в 4 раза - при еще большем и т. д. (см. формулу 24). При полете, находясь в некоторой точке траектории, надо производить один или ряд последовательных взрывов, которые могут изменить начальную траекторию, например, эллиптическую (№ 3) с падением на землю, в другую, тоже эллиптическую (№ 13) с превращением ракеты в спутника земли, или даже в параболическую (№ 14). Наконец, при помощи подобных дополнительных взрывов можно сделать путь спиральным, при чем, если взрывы увеличивают бывшую скорость, то ракета описывает развивающуюся спираль, а если уменьшают, то свивающуюся (№ 15). Сила же тяготения изменяет скорости обратно.
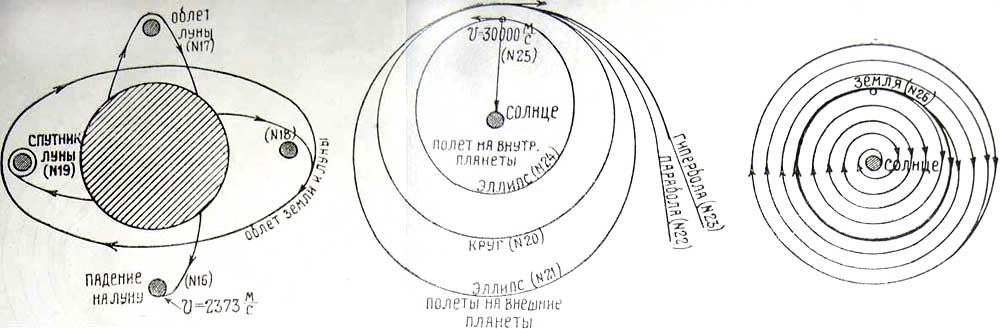
Если ракете сообщить скорость в 30000 м/сек. и в направлении обратном движению земли по орбите, то она упадет солнце (черт. 35 — случай № 25). Если ракета описывает круговую траектор вокруг земли и ей сообщить скорость V= 11170 м/сек, то ракета будет вращаться вокруг солнца (№ 20). Если увеличивать эту скорость взрыванием, то она будет описывать развивающуюся спираль и может достичь внешних планет; при уменьшении же этой скорости спираль будет свивающейся и тогда можно достичь внутренних планет, но сила тяготения будет изменять скорости в обратном порядке.
| I Полет относительно земли | ||||||
| №№ | Направление взлета | Отношение массы взрыв- чат. веществ к собств. массе ракеты М2:M1 | Скорость V м/с | Траектория полета | Результат полета | №№ чертежей |
| 1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 |
Вертикальное с полюса (при- тяжением не- бесных тел пренебрегаем) To же Вертикальное не с полюса To же To же Горизонталь- ное To же To же To же To же To же с эква- тора по напра- влению вра- щения земли Наклонное под 10-15° к го- ризонту То же с допол- нительным взрывом в апо- гее To же Наклонное с дополни- тельными взры- вами (постоян- ными) Наклонный по- лет на луну То же при про- махе попада- ния на луну То же То же с допол- нительным взрывом |
<8 8 < 8 8 > 8 <3-4 3-3 > 3-4 8 > 8 < 3-4 < 3-4 > 3-4 8 < 8 < 8 8 < 8 < 8 |
< 11170 < 11170 11170 11170 > 11170 <7904 7904=11170 > 7904 11170 > 11170 7904-463=
= 7441
< 7904 > 7904 11170 < 11170 < 11170 11170 < 11170 < 11170 |
Прямая ли- ния To же Эллипс Парабола Гипербола Эллипс, па- рабола или гипербола Круг Эллипс Парабола Гипербола Круг Эллипс Эллипс Парабола Спираль Эллипс Эллипс Сложная кривая Эллипс и круг |
Обратное паде- ние на землю Бесконечное удаление Обратное паде- ние Удаление в бес- конечность To же Падение на землю Спутник земли по кругу Спутник земли по эллипсу Удаление в бес- конечность To же Спутник земли по кругу Падение на землю Спутник земли по эллипсу Удаление в бес- конечность К земле или от земли Падение на луну V= 2373 м/с Облет луны и возвращение на землю Движение во- круг земли и луны Спутник луны |
34 (№ 1) 34 (№ 2) 34 (№ 3) 34 (№ 4) 34 (№ 5) 34 (№ 6) 34 (№ 7) 34 (№ 8) 34 (№ 9) 34 (№ 10) 34 (№ 11) 34 (№ 12) 34 (№ 13) 34 (№ 14) 34 (№ 15) 35 (№ 16) 35 (№ 17) 35 (№ 18) 35 (№ 19) |
| II Полет относительно солнца | ||||||
| 20 21 22 23 24 25 26 |
Движение зем- ной орбите To же To же To же To же To же То же при до- полнительном непрерывном взрывании |
7-8 < 7-8 20 20 > 7-8 200 7-8 |
11170 < 11170 16300 76300 > 11170 -30000 > <11170 |
Круг Эллипс Парабола Гипербола Эллипс Эллипс Спираль |
Спутник солнца Спутник солнца Полет на внеш- ние планеты Удаление к но- вой солнечн. системе To же Спутник солнца. Полет на вну- трен. планеты Падение на солнце Приближение или удаление от солнца |
35 (№ 20) 35 (№ 21) 35 (№ 22) 35 (№ 23) 35 (№ 24) Энергия па- дения на Меркурия = 1/5 тако- вой же на землю, а на Венеру = = 0,82. 35 (№ 25) 35 (№ 26) |
В 1914 году К. Циолковский выпустил в свет новую небольшую брошюру „Исследование мировых пространств реактивными приборами“. (Дополнение к I и II части труда того же названия). Калуга. В ней он как бы подводит итоги своим работам, резюмируя их в виде следующих теорем:
Теорема 1. Пусть сила тяжести не уменьшается с удалением тела от планеты. Пусть это тело поднялось на высоту, равную радиусу планеты; тогда оно совершит работу, равную той, которая необходима для полного одоления силы тяжести планеты (см. выше стр. 71 и формулу 36).
Теорема 2. В среде без тяжести окончательная скорость ракеты при постоянном направлении взрывания не зависит от силы и порядка взрывания, а только от количества взрывчатого материала (по отношению к массе ракеты), и также от качества и устройства взрывной трубы (см. стр. 58 и формулу 6).
Теорема 3. Если количество взрывчатого материала равно массе ракеты, то почти половина работы взрывчатого вещества передается ракете (см. табл. II при ![]() = 1).
= 1).
Теорема 4. Когда масса ракеты плюс масса взрывчатых веществ, имеющихся в реактивном приборе, возрастает в геометрической прогрессии, то скорость ракеты увеличивается в прогрессии арифметической (см. стр. 58 и формулу 6).
Например, когда массы увеличиваются в отношении 2, 4, 8, 16, 32 64,.... то скорости массы увеличиваются в отношении 1, 2, 3, 4, 5,... или в числах:
| Массы взрывчатого вещества | 1, 3, 7, 15, 31, 63, 127, 256 | для водорода и кислорода |
| Скорости км/сек. | 3½, 7, 10½, 15 17½, 21, 24½, 28 | |
| Скорости км/сек. | 3, 6, 9, 12, 15, 18, 21 | при бензоле или бензине |
Теорема 5. В среде тяжести, например, на земле, при вертикальном поднятии ракеты, часть работы взрывчатых веществ пропадает и тем большая часть, чем ближе давление вырывающихся газов на ракету к весу последней (см. стр. 60 — 62).