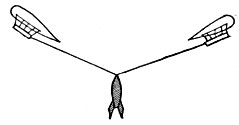
Обозначим:
время взрыва
скорость истечения газов через С
массу выброшенную из ракеты черев dm
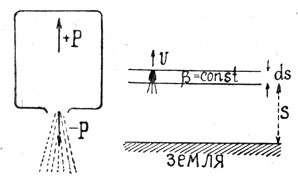
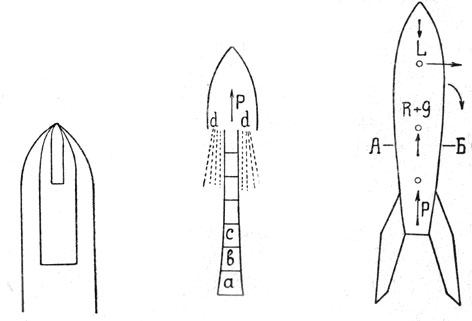
На фиг. 35 изображена ракета в продольном разрезе. При взрыве внутри ее, газы вырываются через сопло внизу, а отдача толкает ракету вверх.
Обозначим: | величину отдачи через Р время взрыва скорость истечения газов через С массу выброшенную из ракеты черев dm |
На основании закона количества движения имеем
Расход горючего с течением времени определяется из уравнения (1) путем интегрирования
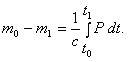
Обозначим через: | L — сопротивление воздуха полету ракеты G — вес ракеты (сила тяжести) Q = L + G v — скорость полета в данный момент b — ускорение ее полета = R — P — Q — силу, сообщающую ракете ускорение b. m — массу ракеты. |
Это и есть основное дифференциальное уравнение движения, связывающее массу, скорость, время, расход горючего и силы сопротивления.
 Фиг. 35. |
Рассмотрим движение ракеты в пределах земной атмосферы и определим ту скорость ее движения, при которой 1) количество движения mdv, определяющее полет ракеты, сохраняет заданную величину и 2) расход горючего — dm — будет minimum. Назовем такую скорость наивыгоднейшей.
Пусть ракета (фиг. 36) на высоте s над землей проходит слой воздуха такой малой толщины ds, что за время его прохождения: 1) плотность его не меняется, 2) масса m ракеты тоже не меняется*), 3) а количество движения возрастает постоянно на mdv.
* Здесь автор допускает противоречие: m не будет постоянно, а будет уменьшаться.
Тогда время прохождения этого слоя будет ![]() и из уравнения (2) получим
и из уравнения (2) получим
Выражения mdv и ds мы считаем постоянными. Дифференцируя по v получим
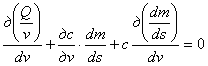 ........ (3)
........ (3)Для своей ракеты Оберт полагает скорость истечения газов (с) постоянной. Тогда второй член уравнения (3) обращается в нуль. Условие же, что расход горючего dm должен быть minimum, дает
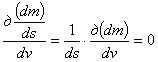 ,
,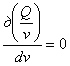 ........ (4)
........ (4)Но Q = L+G; где G — сила тяжести = mg, а g — ускорение силы тяжести на высоте s. Для слоя ds принимаем g= const., a L — сопротивление воздуха, равное
где F — площадь миделевого сечения ракеты.
β — плотность воздуха.
γ — коэффициент сопротивления воздуха, зависит от формы ракеты, и от скорости v.
Подставляя эти значения в выражение Q, получим
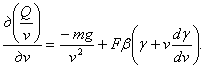
Когда это выражение равно нулю, то и получается наивыгоднейшая скорость, определяемая из условия
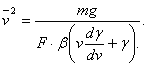 ........ (5)
........ (5)В дальнейшем везде и принята именно эта наивыгоднейшая скорость, что значительно упрощает все выкладки.
Из (5) имеем
Здесь все переменные являются функцией одной лишь независимой v.
Дифференцируя, получаем
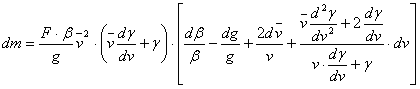 ........ (5b)
........ (5b)Обозначая
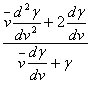
Разделив (5с) на 5а, получим
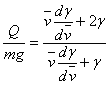 ........ (5d)
........ (5d)Это выражение мы обозначаем через у.
Уравнение (2) или, что то же, (2а), связывало между собою массу, время полета, силу, путь, расход горючего и скорость полета ракеты. Преобразуем его, введя вместо скорости (v) наивыгоднейшую скорость v полета ракеты.
Умножая все части уравнения (2а) на ![]() получим
получим
Но из 5a и 5b имеем
Из 5d
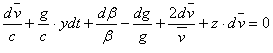 ........ (6a)
........ (6a)Далее Оберт выражает все переменные уравнения (6а) через v и t.
Ускорение силы тяжести g обратно пропорционально квадрату расстояния от центра земли. Если r радиус земли и s — высота полета, то
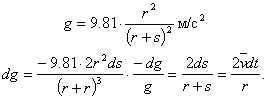
Во втором члене формулы (6а) в виде первого приближения предположим g равным в среднем 9.7 м/с2 (для s0=5; s1 = 50 км), получим
Для определения 3-го члена формулы (6а) Оберт принимает для удобства интегрирования приближенное выражение плотности воздуха от высоты
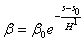
Дифференцируя по s, получим
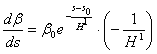
Подставляя полученные выражения в (6а), имеем
Обозначая
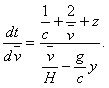 ........ (7)
........ (7)Время полета.
Если принять скорость v свыше 460 м/с, то коэффициент сопротивления воздуха (γ) для этого случая, на основании баллистических опытов, можно принять постоянным, тогда имеем из (5d)
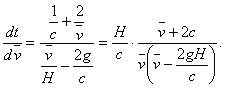 ........ (7a)
........ (7a)Интегрируя, получаем
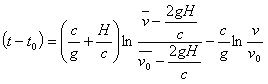
Ускорение (b) получаем из (7а)
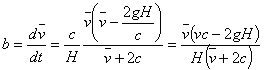 ........ (7c)
........ (7c)Определение массы.
Подставляя в (6) значение
Величина силы отдачи Р определяется из (1)
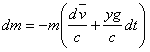 ........ (8)
........ (8)Высота подъема: ds = v·dt; принимая во внимание (7а):
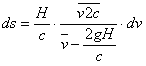 ........ (10)
........ (10)Интегрируя
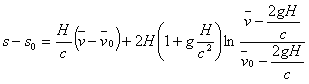 ........ (10a)
........ (10a)Пример подсчета:
пусть Н = 6300 метр.; v0 = 500 м/с; v1 = 11000м/с; с = 3000м/с; g=9,7м/с2;
тогда члены формулы 10а получают значения
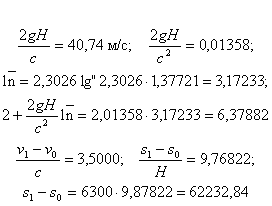
Расход горючего по (8а)
Но t1 — t0 определяется из (7b)
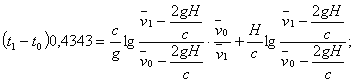
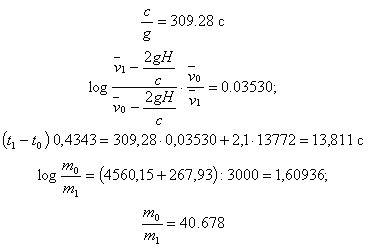
Полученному значению s1 — s0 = 62 232.8 соответствует на высотах s1 и s0 отношение плотностей воздуха
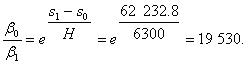
Если предположить, что плотность β, на высоте s1 будет больше, то условия полета конечно изменятся. Оберт проделывает выше приведенный расчет и получает для β1 в 60 раз большей следующие числа
Далее он показывает, что несмотря на не совсем точные принятые значения для плотности воздуха, коэффициента сопротивления воздуха и ускорения силы тяжести g, результаты получаются все же достаточно точными (уклонения не превышают ±7-8%).
Результаты: При подъеме с высоты s0 = 5000 м до высоты s1 = 67 233 м и при начальной массе ракеты m0 и начальной скорости v0 = 500 м/с получаем:
1) Массу ракеты на высоте s1 — m1 = 0,023 m0
2) Скорость v на высоте s1 — 11000 м/с
3) Время подъема — около 19 с.
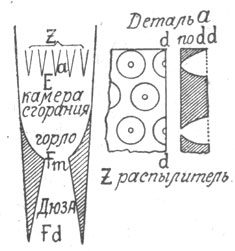 Фиг. 37. |
На фиг. 37 изображена схема движущей (нижней) части ракеты. В качестве горючего применены жидкий кислород и горючая жидкость. Оберт предполагает свою ракету составной, т. е. состоящей из двух частей: верхней и нижней. Каждая из них является самостоятельной ракетой. Нижняя, по использовании своего горючего, отпадает и тогда начинает работать верхняя ракета. Для верхней он в качестве горючей жидкости применяет жидкий водород, а для нижней — смесь воды со спиртом. Смешение жидкости с кислородом происходит в камере сгорания, куда вспрыскивается уже газообразный и нагретый до 700° кислород через боковые стенки трубок Е (деталь стенки трубки со стороны камеры сгорания показана на фиг. 37а отдельно). Снаружи же сверху эти трубки обтекаются горючею жидкостью под давлением 3— 4 атм. Совокупность трубок Е образует распылитель кислорода. Длина их от 3 до 5 см. Под распылителем, в камере сгорания, происходит воспламенение смеси, которая в свободном расширении несколько задерживается, для увеличения отдачи, горлом Fm. Из горла Fm газы выходят, расширяясь, по дюзе через ее отверстие Fd наружу.
Скорость истечения газов в любом месте дюзы Оберт определяет по формуле Цейнера
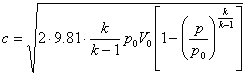 , ........ (12)
, ........ (12)р0 — абсолют. давление в камере сгорания в кг/м2
р0 — „
„
„ в рассматриваемом месте дюзы в кг/м2.
Р — предполагается ≥ давления воздуха β.
V0 — объем газа в м3.
Величина Р0 V0 зависит от смеси газов.
Скорость W возрастает с возрастанием давления Р в камере сгорания, с увеличением R (p·v=RT) (газовая постоянная) и T (абсолютная температура), и убывает с увеличением k (для водорода k=1.4). Давление Р редко превышает 5 атм. и при температуре до 2000° абс. Наибольшую газовую постоянную имеет водород (R = 420), тогда как для кислорода = 26.5, водяного пара = 47, и воздуха 29.26.
Форма дюзы по Цейнеру определяется формулой
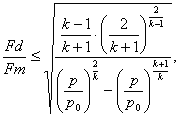 ........ (13)
........ (13)Наружное сечение дюзы Fd Оберт принимает = 705 см2.
Если k и ![]() постоянны, то и
постоянны, то и ![]() постоянно,
постоянно,
где Pd — давление газа у выхода из дюзы.
При этом, по формуле (12), будет и скорость истечения газа из устья дюзы, т. е. Сd — также постоянной и независящей от внутреннего давления газа Р0.
Однако, при возрастании P0 будет возрастать и Pd, а равно отдача Р и масса вырывающегося газа.
Величина отдачи определяется формулой
Из этой формулы следует, что на большой высоте, где β почти, или совсем нуль, отдача сильнее на величину F.
Однако, это утверждение не совсем точно, так как отдачи в действительности будет не настолько больше, по следующим причинам: 1) при уменьшении β происходит расширение газа за дюзой, отчего падает (р), а следовательно уменьшается и pdF; 2) увеличивается скорость истечения с в горле; 3) протекает в Fm больше газа.
Наименьшая величина скорости истечения с Обертом принята от 1530 до 1700 м/с.
Состав горючей смеси Оберт предлагает в виде примера такой:
На 96 г кислорода — 46 г этилового спирта „ |
Количество теплоты, необходимой для нагревания Н кг жидкого водорода до температуры вспышки T1 определяется по формуле — H.3.4 (Т1+12) калорий, где 3.4 = сp — теплоемкость газа при постоянном давлении.
Для нагревания до той же температуры S кг жидкого кислорода потребуется
Если применить вместо кислорода жидкий воздух, то, заключающийся в нем азот, также придется нагреть, а на это потребуется теплоты (при N кг азота)
При вычислении скорости истечения газов, необходимо знать величину k. Она для нижней (спиртовой) ракеты принята k= 1.30, для верхней, где взрываются водород и водяной пар с кислородом, величина k определяется, при разных весовых отношениях составляющих газов, следующей таблицей.
| 0.8 | 0.9 | 1.0 | 1.1 | 1.2 | 1.3 | 1.4 | 1.5 | 1.6 | 1.7 | 1.8 | 1.9 | |
| K...... | 1.400 | 1.398 | 1.396 | 1.394 | 1.393 | 1.391 | 1.389 | 1.388 | 1.386 | 1.385 | 1.384 | 1.383 |
Для двух-атомного газа (кислород) k= 1.406.
После израсходования горючего, начинается свободный полет ракеты в пространстве с некоторою скоростью v1 слагающейся из собственной скорости v1 ракеты и касательной скорости w, которую ракета получила благодаря вращению земли и ветру. Следует заметить, что пока ракета проходит в пределах земной атмосферы, сопротивление воздуха уменьшает скорость свободного полета ракеты, однако, это уменьшение незначительно на больших высотах, и, по вычислению Оберта, при скорости v1 = 1000 м/с. — равно всего 69 м/с, а при v1 = 10 000 м/с — всего лишь 2.2 м/с*, чем можно пренебречь.
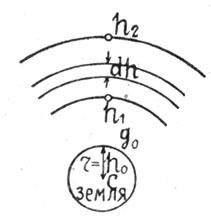 Фиг. 38. |
* Это замедление Оберт определяет по формуле
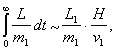
Пусть ракета массы m1 с высоты h над центром земли переместилась на высоту dh (фиг. 38), и пусть ускорение силы тяжести на высоте h равно g. Тогда работа силы земного притяжения на этом пути будет
Когда ракета с высоты h1, поднимется на высоту h2, будет затрачена работа земного притяжения
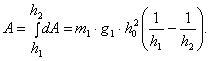 ........(15)
........(15)Так как такой подъем происходит за счет кинетической энергии ракеты, то
Из этих двух формул имеем
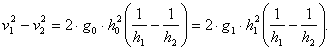 ........(16)
........(16)При выводе этой формулы предполагается, что другие небесные тела не влияют на полет ракеты.
Пока v12 < 2 g1h1 — ракета будет описывать в пространстве эллипс
v12 = 2 g1h1„
„
„
„
параболу
v12 > 2 g1h1„
„
„
„
гиперболу.
По второму закону Кеплера в равные промежутки времени, площади, описанные радиусами векторами орбиты ракеты, будут равны (фиг. 39). На основании этого закона и определяется высота полета
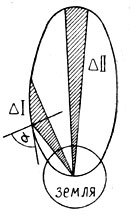 Фиг. 39. |
h1+v1dt·sin α, где α — угол между скоростью v1 и горизонтом.
Площадь ∆-ка ∆I = v1· h1·cos α.·![]()
Стороны ∆-ка ∆II v2dt; h2; h2;
Его площадь ∆II = h2 v2 ·![]()
Приравнивая эти площади, получаем
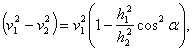
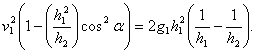
В случае эллиптической орбиты, это уравнение имеет два корня, один для нас мнимый (внутри земли или под нею), другой — действительный, определяющий наивысшую точку подъема.
Ее высота определится из вышеуказанного выражения
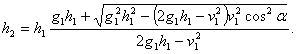 ........(17)
........(17)Если ракета запускается перпендикулярно к поверхности земли, как это Оберт считает для своей ракеты, то предыдущая формула принимает вид
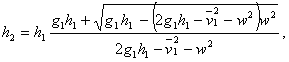 ........(17a)
........(17a)Обратное падение ракеты не произойдет в точку взлета. Это происходит благодаря 1) влиянию ветра, 2) вращению земли и 3) условиям полета ракеты.
 Фиг. 40. |
Действительно, пусть ракета вылетает по направлению радиуса земли из точки (а) на ее поверхности (фиг. 40), имея одновременно с землей вращательную скорость w. Подымаясь вверх до высоты b, ракета, под влиянием двух скоростей v и w, будет двигаться в плоскости этих скоростей, проходящей через центр шара и пересекающей его поверхность по большому кругу ее. Возвращаясь обратно, ракета и должна была бы упасть, где то на этом круге, т. е. она упадет на поверхность земли где-то на этом круге, расположенном к югу от параллели точки (а). Вместе с тем (фиг. 41) вылетая с земли из точки (а), ракета имеет одинаковую с землей угловую скорость, которая по мере подъема ракеты, будет все уменьшаться. Поэтому, когда ракета упадет обратно на землю, она отстанет от точки вылета к западу и попадет не в свою передвинувшуюся точку вылета а1, а западнее ее в какую то точку а2. В результате движения по фиг. 40 и 41, ракета упадет где то на кривой, идущей из точки вылета (а) к югу и западу (фиг. 42).
Мы измеряем вес тела давлением его на некоторую опору, например, на чашку весов. Это давление пропорционально произведению массы тела на ускорение, которым оно обладает. Тело, находящееся на поверхности земли, имеет ускорение силы тяжести g=9.8-9.83 м/с2. Если удалить опору тела, то последнее будет падать.
Назовем термином „эффект ускорения“ результат действия ускорения на тело. По закону относительности движения этот эффект будет происходить: 1) Когда все молекулы тела испытывают ускорение, а само тело находится в покое. Пример: давление гири на чашку весов. 2) Когда все молекулы тела в покое, а тело движется ускоренно. Пример: влияние инерции на пассажиров при резких ускорениях или торможениях трамвая. Эффект ускорения измеряется в тех же мерах, как и само ускорение, т. е. м/с2.
Вычислим в виде примера эффект ускорения при падении биллиардного шара из слоновой кости на мраморную доску.
Данные: | высота падения 20 см. скорость падения v = 2 м/с. деформация при ударе s = 1 мм. |
Обозначим эффект ускорения — а
время, за которое произойдет деформация — t
Имеем формулы для подсчета
Еще примером эффекта ускорения может служить прижимание колес велосипеда в верхнем пункте „чертова колеса“, по которому несется велосипедист, или летчика, описывающего „мертвую петлю“. Здесь причиной эффекта является центробежное ускорение. Влияние эффекта исчезает, когда инерция тела сравнивается с его весом, например, когда тело свободно падает. Если ракета будет свободно падать на землю, то люди в ней потеряют свой вес и будут свободно висеть в воздухе внутри ее, жидкости примут шарообразную форму и перестанут давить на стенки сосуда и т. п. Наоборот, когда ракета получит значительное ускорение движения, то жидкости будут сильнее давить на стенки, что необходимо принять в расчет при проверке прочности сосудов, во избежание их разрыва.
В ранее выведенных формулах, определяющих время полета (t1 — t0) (7а), ускорение в (7с), расход горючего и вообще уменьшение массы ракеты lg ![]() (8а) и удельную отдачу
(8а) и удельную отдачу ![]() (9), можно принять скорость истечения газов с, начальную скорость v0, и начальную высоту Н и ускорение g — данными и постоянными; тогда t1 — t0 b,
(9), можно принять скорость истечения газов с, начальную скорость v0, и начальную высоту Н и ускорение g — данными и постоянными; тогда t1 — t0 b, ![]() и
и ![]() являются функциями скорости v и могут быть вычислены для разных v. Результаты подобных расчетов приведены в таблице (см. стр. 160) для с = 1400 м/с и H= 7200 метров.
являются функциями скорости v и могут быть вычислены для разных v. Результаты подобных расчетов приведены в таблице (см. стр. 160) для с = 1400 м/с и H= 7200 метров.
Пользуясь этой таблицей, можно определить отношение масс ![]() при любом диапазоне скоростей и при иной начальной скорости. Пусть, например, требуется определить отношение масс при начальной скорости va = 800 м/с и конечной vb = 3000 м/с.
при любом диапазоне скоростей и при иной начальной скорости. Пусть, например, требуется определить отношение масс при начальной скорости va = 800 м/с и конечной vb = 3000 м/с.
Так как
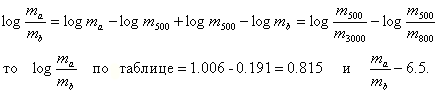
Время подъема: 38.2 — 16.1 = 22.1 с.
| Скорость v м/с | Продолжи- тельность полета (t1 — t0) сек | Ускорение полета в м/с2 | log | Примечание | ||
| 500 600 700 800 900 1000 1200 1400 1500 1700 2000 2200 2400 2600 3000 3400 3800 4000 |
0.0 7.3 11.9 16.1 21.5 21.5 25.2 27.7 29.0 31.2 33.6 35.0 35.9 36.5 38.2 39.3 40.3 40.7 |
11.7 17.0 23.3 30.1 37.8 40.0 64.1 84.3 95.0 117.1 153.7 179.5 206.0 234.0 291.5 351.0 414.0 447.0 |
0.0000 0.0754 0.134 0.191 0.240 0.286 0.371 0.448 0.486 0.550 0.625 0.735 0.808 0.872 1.006 1.138 1.267 1.330 |
1.000 1.190 1.362 1.552 1.738 1.931 2.349 2.803 3.062 3.631 4.217 5.434 6.427 7.446 10.139 13.74 18.49 21.38 | 31.4 30.9 31.4 31.4 33.0 34.1 35.6 37.0 37.2 37.8 41.2 36.7 35.1 34.1 29.9 26.9 23.4 21.8 | m0 — масса наполненной ракеты m — масса ракеты вообще Р — отдача |
Так как отношение ![]() с увеличением скорости и времени полета возрастает весьма быстро и, по техническим соображениям, скоро достигает предела, то Оберт предлагает сделать ракету составной, помещая одну в другую. Каждая ракета имеет свой двигатель и горючее и по сгорании последнего эта ракета отпадает, благодаря чему увеличивается вновь отношение
с увеличением скорости и времени полета возрастает весьма быстро и, по техническим соображениям, скоро достигает предела, то Оберт предлагает сделать ракету составной, помещая одну в другую. Каждая ракета имеет свой двигатель и горючее и по сгорании последнего эта ракета отпадает, благодаря чему увеличивается вновь отношение ![]() остающихся ракет и через это достигается большая скорость.
остающихся ракет и через это достигается большая скорость.
Обозначим массы полных ракет М0, m0
„
ракет без соответствующего горючего М1, m1
тогда в уравнении (8а) вместо ![]() следует подставить
следует подставить
Эту величину мы можем сделать сколь угодно большой, применяя ряд ракет, вложенных одна в другую (в своем аппарате Оберт принимает две ракеты).
Каждая внешняя ракета (фиг. 43) должна быть больше суммы всех остальных и последняя остающаяся ракета должна весить, как можно меньше.
Сверхдавление внутри ракеты полезно в том отношении, что увеличивая натяжение стенок ее и сосудов для горючего, вместе с тем увеличивает и сопротивляемость их изгибу, как это имеет место, например, в баллонах мягких дирижаблей. Такое сверхдавление полезно применять, когда имеется в виду значительно увеличивать ускорение полета.
 | ||
| Фиг. 43. | Фиг. 44. | Фиг. 45. |
Скорость извержения газов (с) по уравнению (12) при данных ![]() и k тем больше, чем больше произведение Р0 V0; последнее тем больше, чем меньше удельный вес вырывающегося газа и чем выше его температура. Больше всего (с) у водорода.
и k тем больше, чем больше произведение Р0 V0; последнее тем больше, чем меньше удельный вес вырывающегося газа и чем выше его температура. Больше всего (с) у водорода.
Способы увеличить скорость полета. Из выражения (5) видно, что скорость полета ракеты будет тем больше: 1) чем меньше давление воздуха, 2) чем больше нагрузка на единицу площади F поперечного сечения ракеты, т.е. чем больше ![]()
Последняя же величина будет значительнее, когда а) ракета достаточно длинна, и b) когда ее удельный вес значителен. Если мы сделаем ракету длинной, то должны принять меры, чтобы сила сопротивления воздуха ее не сломала. Для этого можно было бы поднять выше точку приложения силы отдачи Р (фиг. 44), поместив сосуды с горючим ниже, в виде хвоста (а, b, с, . . . .) и отбрасывая их по мере опоражнивания. Однако, это устройство имеет много конструктивных неудобств. Или, как это и делает Оберт в своей ракете, можно поместить двигатель внизу. На фиг. 45 показано это расположение двигателя. При несовсем прямом полете, возможно поперечное давление воздуха на головную часть ракеты. Тогда, при действии совокупности всех сил, ракета может сломиться по некоторому сечению АБ. Прочность ракеты можно обеспечить внутренним сверхдавлением и особыми ребрами. При полете в нижних слоях атмосферы, когда скорость полета невелика, плотность воздуха значительна и время полета велико, следует, для повышения скорости и отношения увеличивать скорость извержения с. Оберт в своей составной ракете для нижней — спиртовой принимает с=1530 — 1700м/с., а для верхней — водородной — с = 3800-4250 м/с. При этом удельный вес горючего первой ракеты будет в 8 раз больше. Если бы вместо спиртовой ракеты взять две водородных, то весь аппарат был бы в 5 раз длиннее, по объему в 125 раз больше и в 18 раз тяжелее.
Пусть ракета начинает свое отправление с некоторой высоты, где плотность воздуха n-раз меньше, чем у земли. Тогда получаются следующие выводы: а) начальная скорость будет больше, или, при той же v0 — нагрузка на единицу площади поперечного сечения ракеты будет в n-раз меньше. Равным образом уменьшится расход горючего. Свою ракету Оберт предполагает поднять при помощи двух дирижаблей на высоту 5500 метров (фиг. 46), и лишь оттуда пустить ее
 Фиг. 46. |
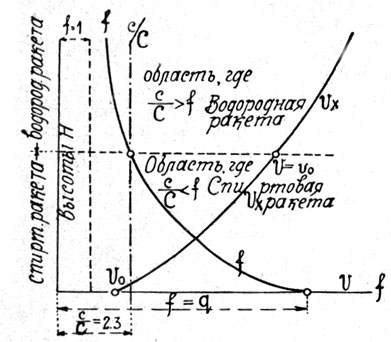
Оберт доказывает, что в нижних слоях атмосферы, где плотность воздуха велика, следует применять спиртовую ракету, скорость извержения газов которой (с) и скорость полета vx относительно малы. В более же высоких слоях, где плотность воздуха мала, следует применять водородную ракету, у которой скорость извержения газов (с) и скорость полета vx больше.
Доказательство применимости разных видов ракет для разных высот Оберт дает следующее:
Отношение ![]() может быть тем больше, чем меньше давление воздуха при начале подъема ракеты.
может быть тем больше, чем меньше давление воздуха при начале подъема ракеты.
Обозначим через br вес горючего и m1 — вес пустой ракеты.
Приблизительно можно принять, что ![]() , где k — коэффициент пропорциональности.
, где k — коэффициент пропорциональности.
Вес горючего спиртовой ракеты в q раз больше, чем водородной. Применим для спиртовой ракеты большие буквы, а для водородной — малые. Тогда имеем
Рассматривая элементарное действие силы отдачи, когда скорость извержения с, расход горючего dm, масса ракеты m и приращение скорости vx, имеем
Для наших двух случаев имеем
Спиртовая ракета:
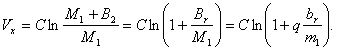
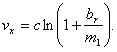
Так как Vх < vx, то
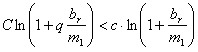
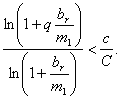 ........(9)
........(9)Отношение ![]() есть постоянное число, равное около
есть постоянное число, равное около
Обозначим левую часть неравенства через f.
Пределы значения f будут
У поверхности земли, где β большое, а ![]() малое, в пределе f=q.
малое, в пределе f=q.
На бесконечно большой высоте, где β = 0
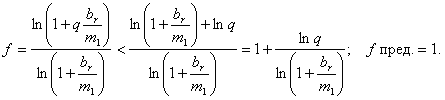
 Фиг. 47 |
Поэтому, там, где должно быть сохранено неравенство (а), применяется водородная ракета, т.е. от высоты, где ![]() = 2.3 и выше (где f < 2,3 и в пределе стремится к 1-це). Ниже же, применима спиртовая ракета для которой
= 2.3 и выше (где f < 2,3 и в пределе стремится к 1-це). Ниже же, применима спиртовая ракета для которой ![]() <q.
<q.
Нами построен показательный чертеж (фиг. 47) иллюстрирующий границы применимости обоих ракет (у Оберта этого чертежа нет).
Соотношение масс ракеты полной и пустой т. е. ![]() могло бы быть произвольно большим там, где нет сопротивления воздуха и земного притяжения.
могло бы быть произвольно большим там, где нет сопротивления воздуха и земного притяжения.
Высота полета ракеты зависит лишь от ее скорости v1 (формулы 16 и 17) и она конечна, пока V12 < 2g1h1. Параболическая скорость будет при условии ![]() и на высоте 70 км над экватором равна 11 160 м/с. Кроме того на высоту полета влияет и широта места (по формуле 17а от широты зависит w).
и на высоте 70 км над экватором равна 11 160 м/с. Кроме того на высоту полета влияет и широта места (по формуле 17а от широты зависит w).
Наибольшая высота полета h по формуле (16) соответствует наибольшей разности V12 — V22 Поэтому, чтобы увеличить h следует увеличивать v1 и уменьшать v2.
Величина скорости v2 будет minimum, если эллипс (фиг. 39) будет как можно более вытянутым, т. е. когда начальная скорость v1 будет отвесной, наоборот, условие, чтобы v1 было maximum, требует, чтобы она по направлению совпадала с касательной к поверхности земли, так как в этом случае к собственной скорости ракеты прибавляется скорость вращения земли. Наивыгоднейшее направление взлета будет заключаться где то между двумя упомянутыми направлениями и будет к востоку. При полете ракеты с параболической скоростью следует ее пускать прямо на восток (по касательной).