К главе II

Приведенные в начале главы II примеры действия силы тяготения могут быть проверены несложными расчетами, основанными, на законе Ньютона и элементах механики. Напомним сначала, что в механике за единицу измерения силы принята сила, которая, будучи приложена к свободному телу в 1 грамм, ежесекундно увеличивает его скорость на 1 сантиметр. Эта сила называется диной. Так как сила земного притяжения ежесекундно увеличивает скорость свободно падающего грамма почти на 1.000 сантиметров (10 метров), то сила, с какой притягивается к Земле 1 грамм, больше „дины" в 1.000 раз, т. е. равна (почти) 1.000 динам. Другими словами: вес гирьки в 1 грамм (сила ее притяжения к Земле) равен 1.000 динам. Это дает нам представление о величине дины в едицицах веса: дина почти равна 1.000-й доле грамма.

Далее: точными измерениями установлено, что два шарика, по 1 грамму каждый, расстояние между центрами которых равно 1 сантиметру, притягиваются между собою с силою в одну 15-миллионную долю дины,. Эту величину часто называют „постоянной тяготения".

Зная это, уже не трудно, пользуясь законом Ньютона, вычислить силу взаимного притяжения двух человеческих тел, разделенных промежутком в 1 сажень (2 метра, или 200 сант.). Принимая вес человеческого тела в 4 пуда, или 65 килограммов (65.000 граммов), и имея в виду, что взаимное притяжение прямо пропорционально произведению масс и обратно пропорционально квадрату расстояния (закон Ньютона), — имеем для силы взаимного притяжения

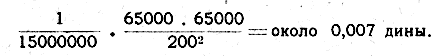
Итак, два человеческих тела притягиваются взаимно с силою 0,007 дины (это менее 100-й доли дины, т. е. менее 100-й доли миллиграмма).

Чтобы вычислить, какой путь пройдут оба тела в течение часа под влиянием этой силы, мы воспользуемся формулой:

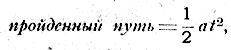
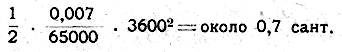
* Здесь сила, действующая на тела, считалась неизменной; это верно лишь приближенно, так как с уменьшением расстояния между телами она возрастает. Но в начале падения, пока расстояние уменьшается незначительно, изменение силы притяжения также весьма мало.

Таким же образом может быть вычислена сила взаимного притяжения и двух дредноутов, разделенных расстоянием в 1 километр. Масса каждого корабля — 25.000 тонн = 25.000.000 килогр. = 25.000.000.000 граммов; расстояние 1 килом. =100.000 сант. Поэтому взаимное притяжение равно

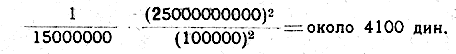
Так как 1.000 дин = 1 грамму, а грамм — около ¼ золотника, то 4.100 дин почти равно 1 золотнику.

Величина сближения кораблей под действием этой силы в течение первого часа равна

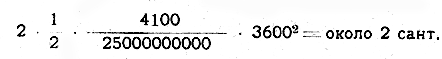
Сложнее вычислить время обращения тяготеющих тел одного вокруг другого (точнее — вокруг их общего центра тяжести), но и этот расчет может быть выполнен элементарным приемом. Вернемся к примеру двух человеческих тел и допустим, что эти тела представляют собою систему обращающихся тел. Массы их равны между собою, а потому оба тела должны обращаться вокруг точки, расположенной в середине между ними, т. е., принимая орбиту за круг, имеем, что радиус ее = 100 сант. Величина центростремительной силы кругового движения равна, как известно из механики, где m — масса, v — скорость, R — радиус круга. Скорость v можно выразить через длину орбиты 2πR, деленную на продолжительность оборота t, т.-е. через . Следовательно,

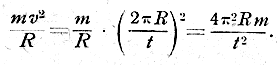
С другой стороны, центростремительная сила должна быть равна силе взаимного притяжения обращающихся тел — иначе кругового движения не могло бы быть. Эта сила выражается формулой

Приравнивая оба выражения:

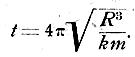
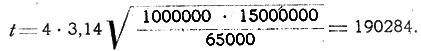
Как вычислить время взаимного падения тяготеющих друг к другу тел, — показано далее, в статье „Падение в мировом пространстве".

В заключение приводим интересный отрывок, характеризующий силу тяготения и заимствуемый у известного английского физика О. Лоджа **:

* Если время обращения и диаметр орбиты известны, то можно вычислить, по той же формуле, неизвестные массы обращающихся тел. Так определяют астрономы массы двойных звезд.
** „Мировой эфир", гл. IX.

„Силы тяготения между небольшими телами незначительны и далеко превосходятся магнитными. Действительно, притяжение между телами определенной малости может быть более чем уравновешено даже давлением, возникающим вследствие их взаимного излучения, несмотря на то, что это давление почти бесконечно мало. Отсюда следует, что достаточно малые тела любой температуры отталкивают друг друга (если только они не заключены в оболочку постоянной температуры, где лучистое давление на них со всех сторон одинаково).

Размеры, при которых лучистое отталкивание перевешивает тяготение, в случае двух равных шаров, зависят от температуры шаров и от их плотности; по данным проф. Пойтинга, при обыкновенной, привычной для нас температуре— скажем, при 16° Ц. — равенство этих двух сил для двух деревянных шаров, расположенных в пространстве, достигается тогда, когда каждый шар имеет диаметр приблизительно в один фут. Для тел меньших размеров или более горячих лучистое отталкивание пересиливает взаимное тяготение; отталкивание это возрастает пропорционально четвертой степени абсолютной температуры тел.

„Притягательная сила тяготения между молекулами чрезвычайно мала; между двумя атомами или двумя электронами она настолько мала, что ею можно пренебречь, хотя бы расстояние между ними и не выходило из пределов размера молекулы.

А между тем, от совокупного притяжения мириад таких тел происходит результирующая сила тяготения, заметная на расстояниях в миллионы миль. Сила эта не только заметна, но величину ее нужно признать прямо-таки ужасающей.

„Когда дело идет о телах астрономических размеров, сила тяготения перевешивает все другие силы; и все электрические и магнитные притяжения в сравнении с нею падают до полного ничтожества".

К главе IV

„Все сделанные попытки объяснить силу тяжести, как результат движения в среде, находящейся между телами, наталкиваются на то затруднение, что тяжесть беспрепятственно проходит сквозь тела, как бы велики и плотны они ни были, — пишет Аррениус *. — Так, например, притяжение Солнца действует на частицу, лежащую в центре Земли, сквозь все промежуточные слои. А так как действие силы должно состоять в каком-нибудь изменении движения тела, подвергающегося ее влиянию, то необходимо принять, что частица, лежащая позади другой, подверженной той же силе, по крайней мере отчасти закрыта от этого влияния. Поэтому на соединительной линии между частицею в центре Земли и любою частицею на Солнце не должна была бы лежать ни одна из бесконечно большого числа тяжелых частиц верхних слоев Земли. Значит, необходимо предположить, что частицы, на которые действует сила тяжести, имеют бесконечно малое протяжение и должны считаться математическими точками. Физически этот взгляд немыслим. Точно также невозможно представить себе, чтобы математические точки могли возмущать движение. Удивительно, что та самая сила природы, которую мы точнее всего можем проследить посредством вычисления, в физическом отношении представляет величайшую загадку".

* Аррениус, „Физика неба".

Совершенно особым образом подходит к вопросу новейшая (1915 г.) теория тяготения, разработанная А. Эйнштейном, которая вовсе не рассматривает тяготение как некоторую „силу". Исходным пунктом теории тяготения Эйнштейна являются следующие соображения: *

* Приводимый далее отрывок заимствован из книги проф. О. Д. Хвольсона „Теория относительности А. Эйнштейна и новое миропонимание" (Пг., 1922).

„Вообразим себе систему в виде большого ящика или комнаты и положим сперва, что она находится в гравитационном поле, т. е. в такой части пространства, в которой действуют силы тяготения, и что она в этом пространстве неподвижна. В виде примера представим себе, что она находится на земной поверхности, где гравитация, т. е. сила тяжести, действует вертикально вниз от потолка к полу комнаты. Наблюдатели, находящиеся в этой системе, заключают следующее. Тела, спокойно лежащие на полу, на столе и т. д., производят давление на тела, находящиеся под ними. Если взять в руку какое-либо тело, напр., свинцовый шарик, и отпустить его, то он начинает падать вертикально вниз с ускорением, которое мы обозначим буквой g, и которое оказывается независящим от рода тела, если исключить сопротивление воздуха. Если шарик бросить в горизонтальном направлении, то он начнет двигаться по кривой линии (по параболе) вниз, и на некотором расстоянии от наблюдателя достигнет пола. В обоих случаях мы имеем дело с весомой массой взятого тела.

„Теперь рассмотрим другой случай. Та же система находится в пространстве, в которого нет никакого гравитационного поля, но сама система движется с ускорением g по направлению, обратному тому направлению, в котором раньше действовала гравитация, т. е. [движется] по направлению от пола к потолку. Наблюдатель, находящийся внутри системы, замечает следующее. Все тела, спокойно лежащие на неподвижных предметах (пол, стол, рука), производят давление на свои опоры; такое же давление производит и сам наблюдатель хотя бы на пол ящика. Если наблюдатель выпустит из рук какой-нибудь предмет, напр., свинцовый шарик, то он увидит, что шарик движется по направлению к полу с ускорением g, между тем как наблюдателю, находящемуся вне ящика, тот же шарик представится неподвижным. Если наблюдатель бросит шарик по направлению, параллельному полу, то заметит, что шарик движется по кривой линии и на некотором расстоянии ударяется об пол. Наблюдателю, находящемуся вне ящика, представится, что шарик движется прямолинейно и равномерно по направлению, параллельному полу. Ясно, что для этого наблюдателя движение происходит по инерции и зависит от инертной массы шарика.

„Сравнивая явления, наблюдаемые в указанных двух случаях внутри системы, мы видим, что они вполне тождественны, хотя в первом случае они зависят от весомой массы тел, а во втором случае — от массы инертной. Наблюдатель, находящийся внутри ящика, не имеет возможности отличить эти два случая друг от друга, и он, например, во втором случае может предположить, что внутри ящика действует гравитационное поле. Все изложенное приводит нас к результату огромной важности. Наблюдатель, находящийся внутри системы, не имеет возможности отличить друг от друга прямолинейного равномерно-ускоренного движения системы от наличности внутри системы гравитационного поля. Все явления происходят внутри системы совершенно одинаково в обоих случаях. Мы можем сказать, что гравитационное поле и равноускоренное прямолинейное движение системы друг другу эквивалентны *. Для Эйнштейна эквивалентность настолько полна, что он вообще всякое ускорение системы отождествляет с возникновением гравитационного поля".

* Читатель уже имел случай убедиться в существовании этой эквивалентности, когда обсуждались (см. стр. 65) условия, господствующие внутри пушечного ядра Жюля Верна в момент отлета. Мы говорили тогда, что так как ядро-каюта движется вверх с ускорением 640 килом, в секунду (в 64.000 раз больше ускорения земной тяжести), то пассажиры должны были чувствовать себя во столько же раз тяжелее обычного. Другими словами, равномерно-ускоренное движение с ускорением 64.000g эквивалентно полю тяготения, в 64.000 раз более сильному, чем земное. — С этим согласуется и тот факт, что внутри свободно падающего ядра пассажиры должны чувствовать себя невесомыми: если весомость их была эквивалентна движению ядра от Земли с ускорением g, то движение в противоположном направлении (к Земле) с тем же ускорением естественно должно уничтожить, эту весомость.

Исходя из этого, Эйнштейн развивает стройную теорию тяготения, принципиально отличную от всех прежде предлагавшихся и уже получившую частичное подтверждение согласием ее неожиданных следствий с наблюдениями.

К сожалению, эта теория не может быть общепонятно изложена.

К главе IV

Вопрос о существовании такого вещества, которое было бы вполне или отчасти непроницаемо для тяготения (т. е. обладало бы свойствами фантастического „кеворита", упоминаемого в романе Уэльса), служил неоднократно предметом научного рассмотрения. До самого последнего времени опыты, производившиеся с целью обнаружить хотя бы следы подробного поглощения тяготения, не давали положительных результатов. Лишь в 1920 г. удалось *, повидимому, получить результат, который указывает на некоторое ослабление силы тяготения, при действии ее через тела большой плотности (ртуть, свинец). При этих опытах свинцовый шар, весом около 1300 килогр., окружался 100 килогр. ртути так, чтобы она не касалась шара: при этом наблюдалось уменьшение веса свинцового шара на 2 миллионные доли грамма.

В другой серии опытов того же ученого тяготение действовало через толстый слой свинца (именно, через призму весом 600 пудов, при этом вес шара уменьшался на 2 миллионных грамма.

Однако, интересные данные этих опытов далеко нельзя считать решающими; они нуждаются в тщательной проверке новыми опытами, с целью установить, действительно ли уменьшение веса в данном случае обусловлено поглощением тяготения, а не гвызывается какими-либо другими причинами *.

* Работа Q. Majoran (см. „Успехи Физических Наук", т. II, вып. 2).

Полет пушечного ядра Жюля Верна на Луну можно рассматривать как случай падения тела в мировом пространстве под влиянием силы тяготения. Поэтому, прежде чем рассматривать условия его полета, полезно рассмотреть такую, например, задачу из области небесной механики:

Во сколько времени упал бы на Солнце земной шар, если бы по какой-либо причине прекратилось его движение по орбите?

Задачи подобного рода легко разрешаются на основании третьего закона Кеплера: квадраты времен обращения (планет и комет) относятся как кубы их средних расстояний от Солнца. В нашем случае мы можем земной шар, летящий прямо к Солнцу, уподобить воображаемой комете, движущейся по сильно вытянутому и сжатому эллипсу, крайние точки которого расположены: одна — близ земной орбиты, другая — в центре Солнца. Среднее расстояние такой кометы от Солнца, очевидно, вдвое меньше среднего расстояния Земли. Вычислим, каков должен был бы быть период обращения этой воображаемой кометы. Составим на основании третьего закона Кеплера, пропорцию:

Период обращения Земли равен 365 сутк.; среднее расстояние ее от Солнца примем за единицу, и тогда ср. расст. кометы выразится ½. Пропорция принимает вид:

Но нас интересует не полный период обращения этой воображаемой кометы, а половина периода, т.-е. продолжительность полета в один конец — от земной орбиты до Солнца: это и будет искомое время падения Земли на Солнце. Оно равно

Итак, чтобы узнать, во сколько времени Земля упала бы на Солнце, нужно продолжительность года разделить на √32, т.-е. на 5,6.

Легко видеть, что полученная простая формула применима не к одной только Земле, но и ко всякой другой планете и даже ко всякому спутнику. Иначе говоря: чтобы узнать, во сколько времени планета или спутник упадут на свое центральное светило, нужно период их обращения разделить, на √32, т.-е. на 5,6. Меркурий, обращающийся в 88 дней, упал бы на Солнце в 15½ дней; Нептун, период обращения которого равняется 30 нашим годам, — падал бы на Солнце в течение 5½ лет. А Луна упала бы на Землю в 27,3:5,6, т.-е.. почти ровно в 5 дней. И не только Луна, но и всякое вообще тело, находящееся от нас на расстоянии Луны, падало бы на Землю в течение 5 дней (если только ему не сообщена начальная скорость, а падает оно, подчиняясь лишь действию одного земного притяжения). Здесь мы вплотную подходим к задаче Жюля Верна. Легко понять, что столько же времени, 5 дней, должно лететь на Луну всякое тело, брошенное, наоборот, с Земли на Луну с такою скоростью, чтобы как-раз достичь расстояния Луны. Значит, алюминиевое ядро Жюля Верна должно было бы лететь 5 суток, если бы его хотели закинуть на расстояние Луны.

Однако, члены Пушечного Клуба расчитывали закинуть ядро не прямо до Луны, а только до той точки между Землей и Луной, где сила притяжения обоих светил уравновешивается: отсюда ядро под действием своей тяжести само уже упало бы на Луну, притягиваемое ею. Это „нейтральная" точка находится на 0,9 расстояния от Земли.

Вычисление, следовательно, несколько усложняется. Во-первых, нужно вычислить, во сколько времени ядро долетело бы до 0,9 расстояния между Землей и Луной, или, — что то же самое, — во сколько времени тело с этого расстояния упало бы на Землю; во-вторых, надо определить продолжительность падения тела от этой нейтральной точки до Луны.

Для решения первой задачи представим себе, что на 0,9 расстояния от Земли до Луны обращается вокруг нашей планеты небесное тело, и вычислим период обращения этого воображаемого спутника Земли. Обозначив неизвестный период обращения через х, составляем, на основании третьего Кеплерова закона, пропорцию:

Вторую задачу решаем сходным образом. Чтобы вычислить, во сколько времени ядро упало бы с расстояния нейтральной точки до Луны, нужно сначала определить, во сколько времени ядро, находясь на том же расстоянии от Луны, совершило бы вокруг нее полный оборот. Радиус орбиты этого воображаемого спутника Луны равен 0,1 радиуса лунной орбиты, а масса центрального светила (в данном случае Луны) — в 81 раз меньше массы Земли. Если бы масса Луны равнялась земной, то спутник, обращаясь на среднем расстоянии вдесятеро меньшем, чем лунное, совершал бы полный оборот в период y, легко вычисляемый по закону Кеплера:

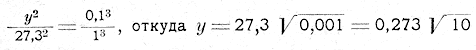
Но так как масса, а следовательно и притягательное действие центрального светила в данном случае в 81 раз меньше, чем в системе Земли, то время обращения ядра-спутника будет дольше. Во сколько раз? Из механики мы знаем, что центростремительное ускорение пропорционально квадрату скорости. Здесь это ускорение (производимое притяжением Луны) меньше в 81 раз, — следовательно, скорость движения ядра по орбите должна быть меньше в √81, т.-е. в 9 раз. Другими словами, ядро в роли лунного спутника должно обегать кругом Луны в 9 раз медленнее, чем оно обходило бы, на таком же расстоянии, вокруг Земли. Значит, искомое время обращения равняется: 0,273√10 × 9 = 7,77 суток.

Чтобы получить продолжительность падения ядра от нейтральной точки до Луны, нужно, как мы уже знаем, найденный сейчас период его обращения (7,77) разделить на √32, т.-е. на 5,6; получим 1,4 суток *.

* На расстоянии Земли ядро обращалось бы вокруг Луны в 9 раз медленнее, чем Луна вокруг Земли, то-есть совершала бы полный оборот в 27,3 X 9 суток. Время падения его на Луну под действием ее притяжения равнялось бы, следовательно, = почти 44 дня. Столько времени должен был бы падать с Земли на Луну „кеворитный" снаряд Уэльса, если бы падение происходило без начальной скорости по прямой линии (точнее, немного меньше 44 суток, так как снаряд падает не от центра Земли к центру Луны, а от поверхности к поверхности).

Итак, весь перелет пушечного снаряда от Земли до Луны должен был бы длиться 4,1+1,4 сут. = 5,5 сут.

Это, конечно, не вполне точный результат: здесь не принято во внимание то обстоятельство, что и при полете от Земли до нейтральной точки ядро подвергается притягательному действию Луны, ускоряющему его движение; с другой стороны, при падении от этой точки на Луну оно испытывает на себе замедляющее действие земного притяжения. Последнее действие должно быть особенно заметно и, как показывает более точное вычисление, почти вдвое увеличило бы продолжительность падения ядра от нейтральной точки до Луны. Благодаря этим поправкам, общая продолжительность перелета снаряда от Земли до Луны с 5½ суток возрастает до 6½ суток.

В романе продолжительность перелета определена „астрономами Кембриджской обсерватории" в 97 час. 13 мин. 20 сек., т.-е. в 4 с небольшим суток, вместо 5½ и даже 6½ суток. Жюль Верн ошибся на двое суток. Повидимому, французский романист, или лицо, производившее для него расчеты, преуменьшили время падения ядра от нейтральной точки до Луны: в романе оно определено всего в 13 час. 53 мин., между тем как, вследствие слабости лунного притяжения, это падение должно было совершаться гораздо медленнее и занять около 60 часов.

В заключение, рассмотрим случай взаимного падения друг на друга тел равной массы. Строго говоря, мы имеем взаимное падение во всех случаях: когда ядро падает на Луну, или камень на Землю, то и Луна одновременно падает на ядро, а Земля на камень. Но скорости перемещения огромных масс Луны и Земли в этих случаях так ничтожны, что ими пренебрегают: они меньше скорости падения ядра или камня во столько же раз, во сколько масса Луны или Земли больше массы или камня. Иное дело, когда массы тяготеющих друг к другу тел равны (или близки по величине): тогда скорости падающих друг на друга тел равны (или близки к равенству), и рассматривать процесс падения тел как процесс односторонний уже нельзя.

Итак, остановимся на примере взаимного падения двух звезд двойной звезды в случае равенства их масс. Установим зависимость между продолжительностью такого падения и периодом обращения звезд по их круговой орбите. Вообразим, что обе звезды, вместо того, чтобы обращаться по кругу радиуса В, движутся по весьма вытянутому эллипсу, „большая ось" которого совпадает с одним из диаметров круга. Среднее расстояние звезды, при таком движении, от общего центра тяжести системы (вокруг которого фактически совершается обращение) равно

Применяя к обеим парам третий закон Кеплера, имеем

Обозначив период кругового движения через t, имеем

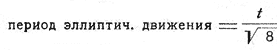
Но легко сообразить, что искомое время падения звезды от точки круговой орбиты до центра составляет ⅓ периода полного обращения по крайне вытянутому эллиптическому пути, — т.-е. искомое время падения =

Выше, на стр. 96-й, мы вычислили, что два человеческих тела должны были бы, обращаясь вокруг общего центра тяжести по круговой орбите диаметром 2 метра, совершать полный оборот в 53,6 часа. Разделив этот период на 11,28, получим продолжительность взаимного падения

К главе VII

Дальность полета ядер, извергаемых новейшими пушками (1922 г.), превзошла даже и те невероятные расстояния, которые преодолевались к концу мировой войны германской артиллерией (т.-е. 80—100 верст). Это стало возможным, главным образом,, благодаря тому, что ядра с большою начальною скоростью закидываются на высоту, где сопротивление воздуха, вследствие его разреженности, весьма незначительно. Снаряд весом 100 килогр. (6 пудов), извергнутый с начальной скоростью 1400 метров (1⅓ версты), быстро проносится через низшие, сравнительно плотные, слои атмосферы и уже на высоте 30 километров попадает в область, где воздух раз в 80 реже, чем близ земной поверхности *. Здесь сопротивление среды настолько незначительно, что ядро может пролететь большое расстояние без заметного уменьшения своей скорости.

* На высоте 40 килом, воздух в 400 раз реже, а на высоте 60 кил. — в 8000 раз реже, чем у поверхности земли.

По газетным сведениям, в Соединенных Штатах Америки уже сооружаются орудия с дальностью полета ядер 200 — 300 верст!

Надо упомянуть еще, что кроме взрывчатых веществ, существует и другое средство сообщить метаемому снаряду большую начальную скорость: выталкивание электромагнитными силами. Теоретически и лабораторно электромагнитные пушки вполне разработаны и оправдывают уже и в настоящее время возлагаемые на них надежды. Теоретики воздухоплавания не отрицают даже возможности полетов людей на таких аппаратах — т.-е. реального осуществления Жюль-Вернова ядра.. „Электрические методы сообщения снаряду начальной скорости, достаточной не только для короткого полета, но даже для прохода весьма значительной дистанции, уже составляют столь крупный шаг вперед в технике аппаратов, основанных на принципе поддержания при помощи начальной скорости, что возможность осуществления полетов на таких аппаратах не может быть вполне отрицаема: необходимо разработать метод безопасного спуска таких снарядов и ограничить развитие внутри его температуры [вследствие трения о воздух] в допустимых для „человека пределах (А. Вегенер. „Самолет будущего", „Вестник Возд. Флота", 1922, № 13).

К главе VIII

Для читателей, которые пожелали бы проверить расчеты, упомянутые на стр. 65-й, приводим здесь эти несложные вычисления.

Для расчетов нам придется пользоваться лишь двумя формулами ускоренного движения, именно:

1) Скорость v в конце t-ой секунды равна at, где а — ускорение:

2) Пространство S, пройденное в течение t секунд, определяется формулой:

По этим двум формулам легко определить (разумеется, только приблизительно) ускорение движения ядра, когда оно скользило в канале грандиозной Жюль-Верновой пушки.

Нам известна из романа длина пушки — 210 метров: это и есть пройденный телом путь S. Романист указывает и скорость ядра у выхода из орудия: 16.000 метров. Данные эти позволяют нам определить прежде всего величину t — продолжительность движения снаряда в канале орудия (рассматривая это движение, как равномерно-ускоренное). В самом деле:

Итак, оказывается, что ядро скользило внутри пушки всего ¹/40 секунды.

Значит, ускорение ядра при движении в канале = 640.000 метров в секунду, т. -е. в 64.000 раз больше ускорения силы земной тяжести!

Какой же длины должна быть пушка, чтобы это ускорение было всего в 20 раз больше ускорения тяжести (т.-е. равнялось. 200 метрам)?

Это задача, обратная той, которую мы только-что решили. Данные: a = 200 метров; v= 11000 метров (при отсутствии сопротивления атмосферы такая скорость достаточна)..

Из формулы v = at имеем: 11000 = 200t, откуда t=55 секундам.

Из формулы получаем, что длина пушки должна равняться метров, т.-е. круглым. счетом около 300 верст.

К главе IX

„Когда я явился к Кибальчичу, — говорил судьям, его защитник, — меня прежде всего поразило, что он был занят совершенно иным делом, ничуть не касающимся настоящего процесса. Он был погружен в изыскание, которое он делал о каком-то воздухоплавательном снаряде; он жаждал, чтобы ему дали возможность написать свои математические изыскания об этом изобретении. Он их написал и представил по начальству".

Начальник жандармского управления, получив рукопись Кибальчича, передал ее в департамент полиции. Там решили, что „давать ее на рассмотрение ученых теперь едва ли своевременно и может вызвать только неуместные толки", — а потому проект был запечатан в конверт и подшит к делу. С 1882 г. по август 1917 г. пакет хранился нетронутым в секретных архивах департамента полиции. Вся история авиации — от первых попыток Райтов до мощных военных аэропланов — успела развиться, — а проект русского революционера, одна из самых смелых технических идей, какие когда-либо рождались в уме человека — лежал безвестно для мира в архивной пыли.

Ниже мы приводим извлечение из этой рукописи Кибальчича (помеченной 23 марта 1881 г.):

„Находясь в заключении, за несколько дней до своей смерти, я пишу этот проект. Я верю в осуществимость моей идеи, и эта вера поддерживает меня в моем ужасном положении.

„Если же моя идея, после тщательного обсуждения учеными специалистами, будет признана исполнимой, то я буду счастлив тем, что окажу громадную услугу родине и человечеству. Я спокойно тогда встречу смерть, зная, что моя идея не погибнет вместе со мной, а будет существовать среди человечества, для которого я готов был пожертвовать своею жизнью. Поэтому я умоляю тех ученых, которые будут рассматривать мой проект, отнестись к нему как можно серьезнее и добросовестнее и дать мне на него ответ как можно скорее.

„Прежде всего считаю нужным заметить, что, будучи на свободе, я не имел достаточно времени, чтобы разработать свой проект в подробностях и доказать его осуществимость математическими вычислениями. В настоящее же время, я, конечно, не имею возможности достать нужные для этого материалы. Следовательно, эта задача — подкрепление моего проекта математическими вычислениями — должна быть сделана теми экспертами, в руки которых попадет мой проект. Кроме того, я не знаком с той массой подобных же проектов, которая появилась за последнее время, т.-е., вернее сказать, мне известны приблизительно идеи этих проектов, но неизвестны те формы, в каких изобретатели думают осуществить свои идеи. Но, насколько мне известно, моя идея еще не была предложена никем.

„В своих мыслях о воздухоплавательной машине я прежде всего остановился на вопросе: какая сила должна быть употреблена, чтобы привести в движение такую машину"?

Отвергнув возможность применения к этой цели силы пара, электричества и мускульной силы человека, Кибальчич приходит к заключению, что источником применимой к воздухоплаванию силы могут быть лишь медленно горящие взрывчатые вещества.

„В самом деле, при горении взрывчатых веществ образуется более или менее быстро большое количество газов, обладающих, в момент образования, громадной энергией. Я не помню в точности, какую работу, если выразить ее в килограммометрах, производит воспламенение 1 фунта пороха, но, если не ошибаюсь, 1 фунт пороху, будучи взорван в земле, может выбросить земляную глыбу, весящую 40 пудов. Словом, никакие другие вещества в природе не обладают способностью развивать в короткий промежуток времени столько энергии, как взрывчатые.

„Но каким образом можно применить энергию газов, образующихся при воспламенении взрывчатых веществ, к какой-либо продолжительной работе? Это возможно только под тем условием, если та громадная энергия, которая образуется при горении взрывчатых веществ, будет образовываться не сразу, а в течение более или менее продолжительного промежутка времени.

„Если мы возьмем фунт зернистого пороху, вспыхивающего при зажигании мгновенно, спрессуем его под большим давлением в форму цилиндра, то увидим, что горение не сразу охватить цилиндр, а будет распространяться довольно медленно от одного конца к другому и с определенной скоростью. Скорость распространения горения в прессованном порохе определена из многочисленных опытов и составляет 4 линии в секунду.

„На этом свойстве прессованного пороха основано устройство боевых ракет. Сущность этого устройства состоит в следующем. В жестяной цилиндр, закрытый с одного основания и открытый с другого, вставляется плотно цилиндр из прессованного пороха, имеющий по оси пустоту в вице сквозного канала; горение прессованного пороха начинается с поверхности этого канала и распространяется в течение определенного промежутка времени к наружной поверхности прессованного пороха; образующиеся при горении пороха газы производят давление во все стороны, но боковые давления газов взаимно уравновешиваются, давление же на дно жестяной оболочки пороха, не уравновешенное противоположным давлением (так как в эту сторону газы имеют свободный выход), толкает ракету вперед по тому направлению, на котором она была установлена в станке до зажигания. Траектория полета ракеты составляет параболу, подобно траектории ядер, выпущенных из орудий.

„Представим себе теперь, что мы имеем из листового железа цилиндр известных размеров, закрытый герметически со всех сторон и только в нижнем дне своем заключающий отверстие известной величины. Расположим по оси этого цилиндра кусок прессованного пороха цилиндрической же формы и зажжем его с одного из оснований; при горении образуются газы, которые будут давить на всю внутреннюю поверхность металлического цилиндра, но давление на боковую поверхность цилиндра будет взаимно уравновешиваться, и только давление газов на закрытое дно цилиндра не будет уравновешено противоположным давлением, так как с противоположной стороны газы имеют свободный выход через отверстие в дне. Если цилиндр поставлен закрытым дном кверху, то, при известном давлении газов, величина которого зависит с одной стороны от внутренней емкости цилиндра, а с другой — от толщины куска прессованного пороха, цилиндр должен подняться вверх".

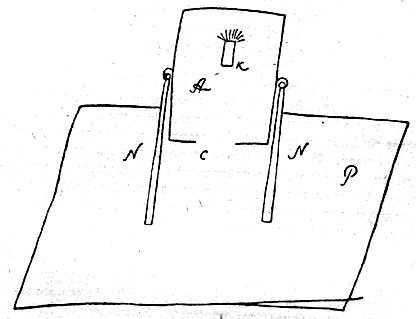
Затем следуют некоторые технические детали проекта. К своему проекту Кибальчич приложил чертеж прибора, который мы здесь воспроизводим (см. рис.). Действие его объясняется в записке так:

„В цилиндре А, имеющем в нижнем дне отверстие С, устанавливается по оси, ближе к верхнему дну, пороховая свечка Д" (так я буду называть цилиндрики из прессованного пороха). Цилиндр А посредством стоек NN прикреплен к средней части платформы Р, на которой стоит воздухоплаватель... Представим теперь, что свечка К зажжена. Через очень короткий промежуток времени цилиндр А наполняется горячими газами, часть которых давит на верхнее дно цилиндра, и если это давление превосходит вес цилиндра, платформы и воздухоплавателя, то прибор должен подняться вверх".

Проект реактивного летательного прибора Н. И. Кибальчича (с собственноручного наброска).

---

К главе IХ

В наши дни идея реактивного аппарата для межпланетных полетов далека еще не только от практического осуществления, но даже и от теоретического воплощения в форме технического проекта. Пройдут, вероятно, сотни лет — писал К. Э. Циолковский в 1911 г., — прежде чем высказанные мною взгляды найдут применение и люди воспользуются ими, чтобы расселиться не только по лицу Земли, но и во всей Вселенной" *. Однако, чтобы дать наглядный пример одной из возможных форм осуществления основного принципа, привожу набросанный, по моей просьбе, К. Э. Циолковским схематический чертеж изобретенного им снаряда и краткое, составленное им, пояснение:

* Впрочем, в печать проникли сведения, что еще в 1909 г. во Франции был выдан одному изобретателю патент на прибор, сходный по идее с реактивным аппаратом Циолковского. В настоящее время (судя по запросам, поступавшим к К. Э. Циолковскому и к автору настоящей книжки) в авиационных кругах Запада существует живой интерес к замечательному проекту нашего соотечественника.

„Снаряд имеет снаружи вид бескрылой птицы, легко рассекающей воздух. Большая часть внутренности занята двумя веществами в жидком состоянии; водородом и кислородом. Они разделены перегородкой и соединяются между собой только мало-по-малу. Остальная часть камеры, меньшей вместимости, назначена для помещения наблюдателя и разного рода аппаратов, необходимых для сохранения его жизни, для научных наблюдений и для управления Ракетой. Водород и кислород, смешиваясь в узкой части постепенно расширяющейся трубы (в роде духового музыкального инструмента), соединяются химически и образуют водяной пар при страшно высокой температуре. Он имеет огромную упругость и вырывается из широкого отверстия трубы с ужасающею скоростью по направлению трубы или продольной оси камеры. Направление давления пара и направление полета снаряда прямо противоположны".

Пополним это описание некоторыми подробностями, заимствованными из научной повести К. Э. Циолковского ,,Вне Земли" (Калуга, 1920):

„Камеры взрывания и трубы, составляющие их продолжение, были сооружены из весьма тугоплавких и прочных веществ, в роде вольфрама*; также и инжекторы [для накачивания элементов взрыва]. Весь взрывной механизм окружался камерой с испаряющейся жидкостью, температура которой была поэтому достаточно низкой. Эта жидкость была одним из элементов взрывания. Другая жидкость помещалась в других изолированных отделениях.

* Вольфрам — один из редких металлов (из него изготовляются, между прочим, нити в некоторых типах так наз. „экономических" лампочек накаливания); он плавится лишь при 3100° (платина — при 1800°) Цельсия.

Я. П.

„Наружная оболочка Ракеты состояла из трех слоев. Внутренний слой — прочный металлический с окнами из кварца, прикрытыми еще слоем обыкновенного стекла, и с дверями, герметически закрывающимися. Второй — тугоплавкий, но почти не проводящий тепла. Третий, наружный, представлял очень тугоплавкую, но довольно тонкую металлическую оболочку. Во время стремительного движения Ракеты в атмосфере наружная оболочка накалялась добела, но теплота эта излучалась в пространство, не проникая сильно через другие оболочки внутрь. Этому еще мешал холодный газ, непрерывно циркулирующий между двумя крайними оболочками, пронизая рыхлую, мало теплопроводную, среднюю прокладку.

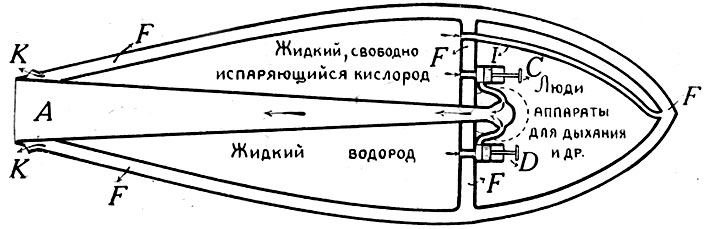Схематический набросок проекта межпланетного дирижабля Циолковского (в разрезе). Труба А и камера из прочного тугоплавкого металла покрыты внутри еще более тугоплавким материалом, — напр., вольфрамом. С и D — насосы, накачивающие жидкий кислород и водород в камеру взрывания В. „Ракета" еще имеет вторую наружную тугоплавковую оболочку. Между обоими оболочками, есть промежуток FFF, в который устремляется испаряющийся жидкий кислород в виде очень холодного газа; он препятствует чрезмерному нагреванию обоих оболочек от трения при быстром движении „Ракеты" в атмосфере. Жидкий кислород и такой же водород разделены друг от друга непроницаемой оболочкой (не изображенной на чертеже). I — труба, отводящая испаренный холодный кислород в промежуток между двумя оболочками; он вытекает наружу через отверстие КК. У отверстия трубы А имеется (не изображенный на чертеже) руль из двух взаимно перпендикулярных плоскостей для управления „Ракетой"; вырывающиеся разреженные и охлажденные газы, благодаря этим рулям, изменяют направление своего движения и таким образом поворачивают „Ракету".

„Сила взрывания могла регулироваться с помощью инжекторов, а также прекращаться и возобновляться. Этим и другими способами можно изменять направление оси снаряда и направление взрывания.

„Температура внутри Ракеты регулировалась, по желанию с помощью кранов, пропускающих холодный газ через среднюю оболочку. Из особых резервуаров выделялся газ, необходимый для дыхания. Другие снаряды были назначены для поглощения продуктов выделения кожи и легких человека. Были камеры с запасами для пищи и воды. Были особые скафандры, которые надевались при выходе в пустое пространство и вхождении в чуждую атмосферу другой планеты. Были камеры с жидкостями для погружения в них путешествующих во время усиленной относительной тяжести; погруженные в них люди дышали через трубку, выходящую в воздушную атмосферу Ракеты. Жидкость уничтожала их вес, как бы он ни был велик в краткое время взрывания. Люди совершенно свободно шевелили всеми своими членами, даже не чувствовали их веса, как он чувствуется на Земле: они были подобны купающемуся, — или же прованскому маслу в вине при опыте Плато...

„Объем Ракеты составлял около 800 куб. метров. Менее третьей доли этого объема (240 к. м.) было занято двумя постепенно взрывающимися жидкостями. Этой массы было довольно, чтобы 50 раз придать Ракете скорость, достаточную для удаления снаряда навеки от солнечной системы и вновь 50 раз потерять ее. Такова была сила взрывания этих материалов. Вес оболочки или самого корпуса Ракеты со всеми принадлежностями был равен 40 тоннам; запасы, инструменты, оранжереи составляли 30 тонн. Люди и остальное — менее 10 тонн. Следовательно, вес Ракеты со всем содержимым был в три раза меньше веса взрывчатого материала. Объем для помещения людей, т. е. заполненного разреженным кислородом пространства, составлял около 400 куб. метров. Предполагалось отправить в путь 20 человек. На каждого доставалось помещение в 20 куб. метров, или около двух куб. сажен..."

Так рисуется в мечтах изобретателя этот межпланетный дирижабль будущего. Желающих познакомиться с работами и идеями К. Э. Циолковского * подробнее отсылаем к его печатным трудам:

* Адрес Конст. Эдуард. Циолковского — Калуга, Улица Жореса, 3.

1. „Исследование мировых пространств реактивными приборами" — напечатано в кратком виде в „Научном Обозрении", (1903, май) и более пространно в „Вестнике Воздухоплавания" (1911 г. №№ 19 — 22 и 1912 г., №Ns 2 — 9).

2. Дополнение к этой работе, напечатанное под тем же заглавием отдельной брошюрой (Калуга, 1914).

3. „Вне Земли" — научная повесть, описывающая воображаемое межпланетное путешествие с помощью реактивного прибора. Печаталась в сокращенном виде в журнале „Природа и Люди" в 1918 г. (не была закончена) и выпущена в полном виде отдельной книгой в 1920 г. в Калуге местным Обществом Изучения Природы.

К главе IX

Укажем, ради полноты, на еще один проект межпланетных путешествий, предложенный в 1915 г. известным французским писателем по вопросам воздухоплавания Анри Графиньи (а еще ранее указанный французами Мас и Друэ). По существу он представляет вариант идеи реактивного снаряда, только получающего свою начальную скорость иным путем.

„Представьте себе колесо огромного диаметра, несущее на окружности снаряд, который должен быть отброшен вдаль. Если при достаточной скорости вращения внезапно освободить снаряд, — он полетит по касательной с той же скоростью, с какой двигалась соответствующая точка колеса. Устройство может быть еще упрощено: машина может состоять из двух параллельных брусьев, закрепленных посредине на оси. Противоположные концы брусьев могут быть снабжены с одной стороны, метательным снарядом, с другой — противовесом. При длине брусьев в 100 метров каждый оборот даст путь в 314 метров; значит, если довести скорость вращения до 44 оборотов в секунду, то крайние точки будут двигаться с секундного скоростью около 14 километров.

„Если пожелаем развить эту скорость в течение нескольких минут, понадобится двигатель, мощностью в миллион лошадинных сил. Это, очевидно, неприемлемо. Оставаясь в пределах существующих технических возможностей, придется действовать медленнее и положить, примерно, семь часов, чтобы добиться 44 оборотов в секунду; тогда достаточен будет двигатель в 12000 лошадиных сил.

„Такая метательная машина должна быть расположена где-нибудь над расщелиной, — напр., между скалами в горах. Она будет приводиться в движение от паровой турбины; а в нужный момент особое электрическое приспособление освободит закрепленный на колесе снаряд, который и полетит вертикально, к зениту...

„Корабль вселенной должен быть снабжен внутренним двигателем, позволяющим увеличить его собственную скорость и управлять его движениями; двигатель не должен быть вовсе особенно сильным, — аппарат, изолированный в пространстве, перемещается с большою легкостью. Мы разумеем двигатель с отдачей", основанный на принципе ракеты; он выбрасывает в пространство массу газа, истечение которого заставит аппарат отклониться.

„Первым следствием работы подобного двигателя является сообщение кораблю постоянно увеличивающейся скорости; это значительно уменьшает длительность межпланетных путешествий. Вторым следствием является замена исчезнувшей силы тяжести ускорением. Мы знаем из опыта, что у человека, поднимаемого кверху с возрастающею скоростью, получается ощущение усиленной тяжести; тот же результат получается и для пассажиров небесного снаряда — они избавятся, благодаря ему, от неприятного ощущения, словно они реют без всякого веса...

„Вес аппарата такого типа достигнет 75 пудов; внутреннее оборудование может быть исчислено в 40 пудов — так что полный вес снаряда — 115 пудов. Прибавляя этот вес к весу провизии на два месяца и трех пассажиров, получим общий вес около 240 пудов.

„Осуществление всего этого не превосходит того, что может быть достигнуто человеческой техникой. Что такое, в самом деле, наш двойной 100-метровый стержень, приводимый в действие двигателем в 12000 лошадиных сил, по сравнению с башней Эйфеля (300 метров) или паровыми двигателями „Лузитании"?

„Можно было бы начать с более скромных опытов. Громадную начальную скорость может дать колесо, даже в 10 раз меньшее, нежели вышеописанное. Можно придать ему скорость в 400 оборотов в секунду помощью турбины типа Лаваля. В шесть часов скорость может быть доведена до 6 километров въ секунду. Такой снаряд может быть отброшен на многие тысячи километров над земной поверхностью — для заатмосферных исследований огромного научного интереса (помощью самозаписывающих аппаратов): ведь мы не знаем даже, что совершается на высоте 60 километров над нашими головами".

К главе X

Положение, что свободно падающее (или брошенное) тело ничего не весит, представляется многим настолько необычным и неожиданным, что его готовы принять за физический софизм (вывод правдоподобный, но ложный). Уместно будет поэтому указать на несколько опытов, могущих подтвердить правильность этого утверждения.

Целый ряд опытов подобного рода был впервые выполнен около 1892—1893 гг. московским физиком проф. Н. А. Любимовым. Из этих остроумных опытов, — странным образом преданных забвению* — укажем следующие:

1. Маятник с твердым стержнем, привешенный к вертикальной доске, отводится в сторону и удерживается в этом положении штифтом. Когда доске с этим маятником дают свободно падать, вынув штифт, удерживавший маятник, то он остается в отклоненном положении, не обнаруживая стремления раскачиваться **.

* В русских книгах (не считая очень редкой теперь брошюры самого Н. А. Любимова) я не нашел упоминания об этих опытах, и только в немецком сочинении Г. Гана «Physikalische Freihandversuche» встречается описание некоторых из них («опыты Н. А. Любимова и Р. Неймана»). Пользуюсь случаем с благодарностью отметить, что первым указанием на принадлежность описываемых далее опытов проф. Н. А. Любимову я обязан любезности проф. А. В. Цингера.
** Это явление принимается в соображение при устройстве для лифтов безопасных приспособлений, которые должны автоматически начать действовать в случае разрыва подъемного каната.

2. К такой же доске прикрепляют стеклянную трубку, в наклонном положении: вверху трубки кладут на ее скошенный край тяжелый шарик, удерживаемый штифтом. В момент падения доски штифт удаляют, — но шарик остается вверху трубки, не скатываясь внутрь ее.

3. На той же доске укрепляют магнит, а под ним на полочку кладут железную полоску (якорь) в таком расстоянии, чтобы магнит не мог ее поднять. Во время падения доски с магнитом и якорем последний притягивается магнитом (так как невесомый якорь уже не надавливает на пружину).

4. „Закон Архимеда утрачивает свое значение при падении системы. Представим себе, что в сосуд с водою погружена пробка (см. рис.). Пружина удерживает ее в воде вопреки давлению жидкости снизу вверх, повинуясь которому пробка всплыла бы наверх. Во время падения сосуда с пробкою этого давления снизу вверх нет [так как давление жидкости обусловлено в данном случае ее весомостью], и пробка опускается вниз". (Н. А. Любимов. „К физике системы, имеющей переменное движение").

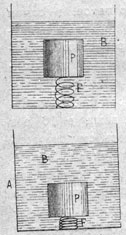Один из опытов проф. Н. А. Любимова: отмена закона Архимеда в падающей системе.

„Явления того же порядка — пишет Н. А. Любимов в сейчас упомянутой брошюре — могут быть наблюдаемы, в известной степени, не только при свободном падении системы, но и в системе, катящейся вниз по наклонной плоскости или качающейся. Опыты с катящейся по наклонной плоскости или качающейся системой могут быть произведены тем с большим удобством, что наблюдатель сам может поместиться в скатывающейся или качающейся системе (катиться с горы, качаться на качелях) и следить за явлением. Нет особого затруднения устроить и свободно падающую систему с помещенным в ней наблюдателем, озаботившись, чтобы падающая система, — напр., корзина на перекинутой через блок веревке — достигала земли без толчка, с утраченною уже скоростью" *.

* В 90-х годах XIX века подобное устройство было предложено (но, кажется, не осуществлялось) во Франции в качестве развлечения для любителей сильных ощущений: камера с посетителями должна была падать с высокой башни в бассейн с водою; погружаясь в воду, камера замедляет свое движение, останавливается и затем всплывает. — Я. П.

Вопрос этот — несмотря на элементарность — почти не затрагивается ни в большинстве учебников, ни в общедоступных книгах по физике. Укажем поэтому несколько сочинений, в которых он рассматривается с той или иной стороны (начинаем с более популярных):

В. Л. Розенберг. Первые уроки физики. 1914.

Я. И. Перельман. Занимательная физика. 1922.

К. Э. Циолковский. Грезы о земле и небе. 1895.

Н. А. Любимов. К физике системы, имеющей переменное движение. 1893.

Герман Ган. Физические опыты. Русск. перевод в изд. «Физика Любителя». 1911. Ч. I. § 48. Сила тяжести.

А. Поспелов. Об относительной потере веса тел в падающей системе. 1913.

Его же. Мир переменной весомости тел. 1913.

К главе X

По поводу настоящей книжки в печати и в письмах к автору высказывалось опасение, что последствия для живого организма от помещения его в среду без тяжести должны быть роковыми. Опасения эти, однако, ни на чем, в сущности, не основаны. Если обстоятельно и систематически рассмотреть, какие именно функции нашего организма могли бы серьезно расстроиться вследствие утраты веса, то окажется, что таких функций нет. „Во время падения или простого прыжка на нашей планете, пока мы еще не коснулись ногами ее почвы, мы также находимся, по отношению к нашему телу, одежде и предметам, при нас находящимся, в среде, свободной от тяжести, но явление это продолжается много-много полсекунды; в течение этого промежутка времени части нашего тела не давят друг на друга, пальто не отягчает плеч, часы не оттягивают кармана. При купании на земле вес нашего тела также почти парализуется противоположным действием воды. Такое отсутствие веса может уже продолжаться неопределенно долгое время. Отсюда видно, что едва ли нужны какие-либо особые опыты для доказательства безвредности среды, лишенной тяжести.

„Если бы даже оказалось, что люди не могут жить без тяжести, то ее легко было бы создать искусственно в среде, где ее нет. Для этого надо только Ракете сообщить вращательное движение; тогда, вследствие центробежной силы, образуется кажущаяся тяжесть желаемой величины, в зависимости от размеров ракеты и скорости ее вращения. Эта тяжесть тем удобна, что может быть произвольно мала или велика, всегда может быть уничтожена и опять возобновлена; но она, как и естественное тяготение, требует усиленной крепости вращающейся Ракеты и других предметов, так как стремится их разрушить (К. Циолковский, „Исследование мировых пространств" *).

* Любопытно, что и усиленная тяжесть, в известных границах, по-видимому, безвредна для живых существ. „Я делал опыты с разными животными, — говорит Циолковский, — подвергая их действию усиленной тяжести на особых центробежных машинах... Вес рыжего таракана я увеличивал в 300 раз, а вес цыпленка раз в 10; я не заметил, чтобы опыт принес им какой-нибудь вред".

Отметим еще неправильность соображения (высказанного некоторыми критиками), будто невесомый воздух внутри межпланетного дирижабля не должен оказывать никакого давления. Если бы это было верно, то, конечно, целый ряд явлений внутри небесного корабля происходил бы не так, как описано в главе X. Но в действительности давление воздуха при данных условиях нисколько не связано с его весомостью. Весомость, конечно, была причиною того, что воздух близ земной поверхности сжат и давит во все стороны. Но этот сжатый воздух должен полностью сохранить свое давление и в том случае, если, в закрытом помещении, он становится невесомым. Ведь сжатая пружина не утрачивает своей упругости в среде без тяжести. Карманные часы не изменят своего хода от перенесения с Земли на Луну или на самый маленький астероид. Сжатый газ — та же пружина, и не должен утрачивать своей упругости при ослаблении тяжести или полной потере веса (если, конечно, газ заключен в герметически замкнутом пространстве). Поэтому барометр-анероид показал бы в летящем небесном дирижабле то же самое давление, какое он показывал там до отлета. Барометр же ртутный не пригоден в таких условиях потому, что он измеряет давление воздуха весом ртутного столба, который в среде без тяжести равен нулю.

В связи с вопросом о возможности межпланетных сообщений интересно коснуться и другой, естественно связанной с ним темы — межпланетных сношений помощью оптических или иных сигналов. Мы ограничимся здесь беглой справкой.

Впервые в серьезной форме вопрос этот был поставлен в первой половине XIX века знаменитым германским математиком Гауссом. Немецкий астроном Груитуйзен, горячий сторонник обитаемости Луны разумными существами, излагает проект Гаусса так:

„Вот основная идея Гаусса; нужно показать жителям Луны то геометрическое построение, с помощью которого обыкновенно доказывается Пифагорова теорема. Средство — культура земной поверхности где-нибудь на громадной равнине. Чтобы изобразить геометрические фигуры, нужно пользоваться контрастом между темными полосами лесов и золотисто-желтыми площадями хлебных полей. Это удобнее сделать в стране, где жители только временно пользуются обрабатываемой землей и, следовательно, легко подчиняются указаниям. Таким образом, выполнение данной мысли не потребовало бы чрезмерных затрат. Гаусс говорил об этом с глубокой серьезностью. Он придумал еще один способ завязать сношения с обитателями Луны. Способ состоит в применении гелиотропа, — прибора, изобретенного Гауссом и могущего служить не только для измерения углов с весьма длинными сторонами, но и для подачи сигналов. По мысли Гаусса, нет даже необходимости составлять из зеркал громадную отражающую поверхность: достаточно известного числа хорошо обученных людей с самыми обыкновенными зеркалами. Следует выбрать время, когда обитатели Луны наверное смотрят на Землю, — например, когда наша планета покрывает Венеру. Зеркала отбрасывают свет по направлению к Луне. Чтобы жители Луны узнали о нашем существовании, нужно прерывать этот свет через равные промежутки времени; так можно сообщить им числа, которые имеют большое значение в математике. Конечно, чтобы эти знаки привлекли внимание, нужно выбрать, подходящий день, когда яркость света, отраженного гелиотропом, будет особенно велика. Гаусс предпочитал математические знаки, потому что у нас и у обитателей далеких миров могуг оказаться общими только основные математические понятия и воззрения".

Попыток осуществить этот проект не делалось.

В 1890-м году много и оживленно обсуждался вопрос о сношении, помощью оптических сигналов, с предполагаемыми обитателями Марса. При таком настроении умов некоторые замеченные на нем явления были приняты за световые сигналы. ,,Как раз в то время, когда пылкие умы старались измыслить средства, чтобы установить сношения между планетами, некоторые наблюдатели, вооруженные весьма сильными телескопами, заметили своеобразные светлые выступы на границе освещенной и ночной половин Марса. Выступы эти держались слишком долго, чтобы их можно было принять за цепь облаков; казалось, обширные области планеты начинали светиться, едва над ними опускалась ночь... Для многих не оставалось сомнения, что здесь мы усматриваем огненные знаки с этого далекого мира. К сожалению, это не подтвердилось: Кемпбелл вполне понятным образом объяснил появление этих светлых выступов, как обширные горные области [залитые светом]... В 1892 г. и 1894 г. светлые места наблюдались опять. Они появлялись всегда в определенных местах, именно лишь в тех желтых областях, которые астрономы считают материками. Кемпбелл дает следующее объяснение этому явлению: „Марс находился от нас на расстоянии 63 миллионов километров. Мы могли брать увеличения в 350 — 520, и планета приближается к нам на расстояние в 180.000 км. и 120.000 км. Расстояние Луны от нас вдвое и втрое больше. Однако, мы можем просто глазом видеть на границе дневной и ночной половин светлые выступы, образуемые горными цепями и большими кратерами" (В. Мейер, „Мироздание"). — Сходные наблюдения и толки повторились и в декабре 1900 г., когда американский астроном Дуглас заметил на Марсе яркое пятно, державшееся в течение часа. Изобретение беспроводного телеграфа направило мысль о межпланетных сношениях на новый путь. Особенно много говорилось об этом в конце 1900 гсда, когда знаменитый американский электротехник Тесла сообщил, что ему удалось заметить загадочные электрические сигналы при производстве опытов на большой высоте. „Тесла наблюдал — читаем мы в английском научном журнале 1901 г. — на специальном приборе повторные электрические колебания, причина которых заставляла его теряться в догадках. Он пришел к мысли, что они обязаны своим происхождением токам, идущим от планет, и теперь он полагает, что было бы вполне возможно посредством усовершенствованного аппарата сноситься с их обитателями. Далее, со слов Тесла, сообщалось, что он приступает к постройке аппарата, "который даст возможность послать на Марс количество энергии, достаточное для воздействия на электрические приемники, в роде телеграфов и телефонов „Я не сомневаюсь — писал Тесла, — что помощью надлежащим образом построенного аппарата возможно переслать энергию на другие планеты, например, на Марс и Венеру, даже при наибольшем их удалении от Земли. Мой метод даст практическое разрешение вопроса передачи и получения сообщений с планет". Однако, эти предположения ни к чему не привели, и вызванная заявлением Тесла горячая полемика в печати вскоре прекратилась*.

* Эти толки о сигналах с планет нашли себе, между прочим, отклик в романе Уэльса „Первые люди на Луне"

Оживление интереса к этой проблеме наступило вновь лишь в самое последнее время. В 1920 и 1922 г. неоднократно отмечались случаи приема радиостанциями таких сигналов, для которых, по некоторым соображениям, затруднительно допустить земное происхождение; это обстоятельство — в связи с тем, что сигналы наблюдались как раз в эпохи наибольшей близости Марса к Земле — побудило искать станцию отправления загадочных сигналов именно на этой планете.

Интересно поэтому рассмотреть, какие физические и технические трудности стоят на пути к осуществлению радиосвязи с планетами на практике.

Прежде всего надо указать, что хотя на земной поверхности для современного радиотелеграфа более не существует уже непреодолимых расстояний, — но передаваться вверх электрические волны могут беспрепятственно всего лишь сотни на две верст. Дело в том, что на высоте 50 — 200 верст простирается слой разреженной атмосферы, отличающийся от нижележащих своею значительною электропроводностью. Такой слой непрозрачен для электрических волн: он частью отражает падающие на него электрические лучи назад, частью поглощает их, не выпуская наружу. Этот экран, охватывающий непроницаемой оболочкой весь земной шар, прозрачен до некоторой степени лишь для тех электрических лучей, которые направлены к точке зенита, — но энергия ослабленных волн, проникающих через зенитное окошечко, черезчур ничтожна, чтобы заставить работать аппараты отдаленных станций. Допустим, — ради внесения определенности в задачу — что чувствительность марсовых приемников одного порядка с чувствительностью самых совершенных земных аппаратов; тогда, для успешной передачи сигнала на ,Марс потребовалась бы, согласно вычислениям специалистов, радиотелеграфная станция не менее чем в 15.000.000 лошадиных сил! Грандиозность такого результата выступит яснее, если напомнить, что величайшая современная радиостанция (в Сан-Франциско) обладает мощностью всего в 10.000 лош. сил, и что совокупная мощность всех механических двигателей русской промышленности довоенного времени не превосходила 5 миллионов лош. сил. Межпланетная радиостанция поглощала бы угля втрое больше, чем все фабрики и заводы России вместе, работая в довоенном масштабе! Если бы вся энергия Ниагарского водопада полностью была употреблена на вращение якоря динамо-машины, то и тогда мы не получили бы мощности, достаточной для передачи радио-сигнала на Марс. Такие же затруднения вероятно, возникли бы и для обитателей Марса, если бы они пожелали установить радиосвязь с нами (их электрические волны, уже проникшие через непроницаемый слой атмосферы Марса, должны были бы отразиться от непроницаемой для электрических лучей наружной оболочки нашей атмосферы). При таких условиях питать надежды на близкую осуществимость радиотелеграфной связи с планетами, конечно, не приходится.