К. П. Станюкович
Некоторые соотношения механики
фотонных ракет
§ 1. Поскольку скорость движения фотонных ракет может быть близкой к скорости света, то закономерности их движения должны описываться соотношениями специальной теории относительности.
В специальной теории относительности постулируется, что физические законы одинаковы во всех системах координат, движущихся прямолинейно и равномерно относительно друг друга (инерциальные системы), и что скорость света всегда имеет одно и то же значение в любой инерциальной системе отсчета.
Важнейшим следствием теории относительности является связь между массой и энергией. Масса имеет энергетическое выражение, а энергия имеет массовый эквивалент. Законы сохранения массы и энергии в теории относительности заменяются одним законом сохранения массы-энергии.
В обычной классической механике в том случае, когда одна система отсчета движется прямолинейно и равномерно относительно другой со скоростью v вдоль оси х, имеют место такие простые преобразования:
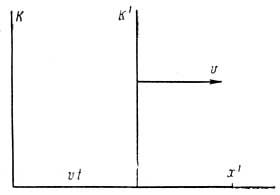
Время и ускорения одинаковы в обеих системах отсчета. Земля при своем движении вокруг Солнца имеет скорость 30 км/сек, что составляет 1/10 000 скорости света. Измеряя и скорость света, идущего от звезды, находящейся впереди по направлению движения Земли, когда скорость Земли складывается со скоростью света, и скорость света от противоположно находящейся звезды, когда скорость Земли вычитается из скорости света, наблюдатели должны были бы получить разницу этих скоростей в 60 км/сек (заметим, что точность измерения скорости света значительно выше и разницу в 60 км/сек можно легко обнаружить). Однако оказалось, что, где бы ни находились звезды, скорость света всегда одинакова. Эйнштейн предположил, что законы сложения скорости обычной классической механики, а, следовательно, и основные законы классической механики неприменимы к таким столь высоким скоростям, как скорость света.
Лоренц впервые, а затем более просто и убедительно Эйнштейн вывели новые соотношения механики, заменяющие прежние.
Постулируя постоянство скорости света во всех инерциальных системах, можно полагать, что величина, называемая интервалом ds, также одинакова во всех инерциальных системах отсчета. В системе отсчета К имеем:
Координаты и времена с индексами (1) и (2) обозначают первое и второе события в системе К'.
Интервал между двумя событиями в обеих системах отсчета одинаков. Доказательство этого положения весьма несложно. Если в одной системе s' = 0, то и в другой системе отсчета s' = 0.
В случае бесконечно близких событий
Мы получили важный результат. Поскольку во всех инерциальных системах отсчета интервал одинаков, то он является инвариантом по отношению к преобразованиям от одной системы отсчета к другой. Эта независимость является следствием постоянства скорости света. Подчеркнем, что интервал определяется четырьмя компонентами, т. е. он определен в четырехмерном квазиэвклидовом мнимом пространстве (пространство Минковского). Можно утверждать, что вообще любой четырехмерный скаляр, определенный в четырехмерном пространстве, будет также постоянен в любой инерциальной системе отсчета, т. е. будет являться инвариантом.
Пусть система отсчета К' опять движется вдоль оси х со скоростью v. Далее, пусть при t1 = t'1 =0 начала координат обеих систем совпадают (х1 = х'1 =0), тогда в любой момент времени при х' = 0 х = vt. Поскольку при этом у = у'; z = z', то из равенства интервалов имеем:
Как мы показали выше и по аналогии с обычной аналитической геометрией для эвклидова пространства можно утверждать, что интервал остается инвариантным (неизменным) при повороте осей х : τ на угол θ; тогда связь между х' : τ ' и х : τ имеет вид:
Из уравнения (8) имеем:
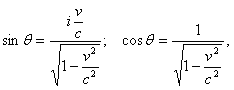
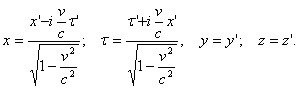
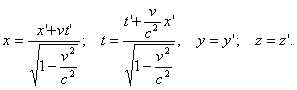
При этом оказывается, что время в разных системах отсчета протекает по-разному, время не абсолютно, как думали раньше, а относительно и, в частности, зависит от скорости движения системы отсчета, в которой оно измеряется.
Деля почленно первое соотношение (10) на второе, найдем, что

Если величина скорости v≪c, то соотношения Лоренца и закон сложения скоростей переходят в классические соотношения, которые называются преобразованиями Галилея.
Легко убедиться в том, что сумма двух скоростей, меньших или равных скорости света, согласно приведенной формуле сложения скоростей, есть скорость, не большая, чем скорость света.
В частности, эта формула показывает, что если u' = с, то и u = с, какова бы ни была скорость v. Таким образом, этот закон сложения скоростей, естественно, удовлетворяет постулату о постоянстве скорости света в любой инерциальной системе отсчета. Скорость света является максимально возможной скоростью в пространстве.
Из преобразований Лоренца можно получить ряд интересных следствий. Мы рассмотрим только два из них.
Допустим, что мы движемся с началом координат системы отсчета К', т. е. движемся относительно системы отсчета К (относительно Земли) со скоростью v. Мы измеряем время t' по нашим часам, в это время на Земле (в системе отсчета К) тоже измеряют время t; связь между обоими временами, поскольку х' = 0, будет иметь вид:
Далее. Мы измеряем длину какого-либо стержня, который расположен по оси х и покоится в системе К. В нашей собственной системе отсчета координаты концов стержня х'2 и х'1. Очевидно, что
Мы видим, что длина стержня как бы сокращается. Если мы пролетаем вдоль стержня со скоростью v, или, что то же, если этот стержень движется относительно нас с той же скоростью, то этот стержень кажется сжатым в отношении
Рассматривая движение ракеты, можно сказать, что система К связана с «неподвижной» Землей, а система К' с движущейся ракетой. В этой системе отсчета скорость ракеты равна нулю. Эту систему отсчета мы и называем собственной системой отсчета.
Скорость ракеты v, скорость какого-либо тела относительно ракеты u', относительно Земли скорость этого же тела u.
Напишем снова выражение для элементарного интервала:
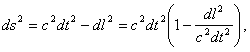
Поскольку ![]() , где u — полная скорость движения какого-либо тела в системе К (движение тела происходит по произвольному направлению, вдоль которого и направлена ось х), имеем:
, где u — полная скорость движения какого-либо тела в системе К (движение тела происходит по произвольному направлению, вдоль которого и направлена ось х), имеем:
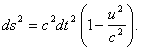
Вычислим теперь ускорение g. Ускорение во всех инерциальных системах одинаково лишь при u→0:
Рассмотрим важную задачу. Пусть в собственной системе отсчета К' дано ускорение, причем движение будем считать прямолинейным. Требуется найти движение относительно системы отсчета К.
Тогда
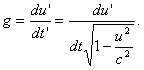
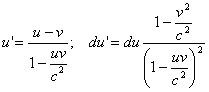
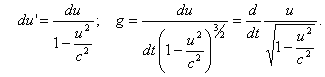
Интегрируя это выражение, найдем, что
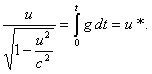
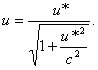
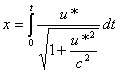
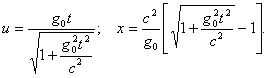
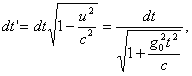
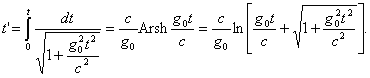
Перейдем к изучению элементов динамики в специальной теории относительности.
§ 2. В релятивистской механике законы сохранения массы и энергии заменяются одним законом сохранения энергии. При различных ядерных (и других) процессах масса тела может изменяться, но полная энергия всегда остается постоянной.
Связь между массой (т) и энергией (Е) дается простым соотношением:
Поскольку положение любой точки в пространстве Минковского определяют вектором, имеющим четыре компоненты: х', у, Z', t, и компоненты этого вектора подчиняются при переходе от одной инерциальной системы к другой преобразованиям Лоренца, то таким же преобразованиям подчиняются и компоненты любого вектора.
Поскольку в пространстве Минковского можно ввести некоторый вектор импульса энергии, три компоненты которого определяют обычные пространственные компоненты импульса, а четвертая определяет энергию, то при переходе от системы отсчета К' к системе отсчета К будут преобразовываться как импульс, так и энергия.
Рассмотрим движение тела, скорость которого в системе К в данный момент времени есть u. В собственной системе отсчета К', которая в данный момент времени имеет скорость относительно К, v = u, u' = 0 (движение вдоль оси х). Компоненты импульса в системе К' I'x = 0, I'y = 0, I'z = 0. Введем формально четвертую компоненту импульса I'τ. Для этой цели вспомним, что в классической механике в системе К
Введем скалярную величину I02=Ix2+Iy2+Iz2+Iτ2. Очевидно, эта величина одинакова в разных системах отсчета (т. е. она инвариантна относительно преобразований Лоренца).
В системе К'
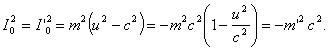
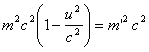
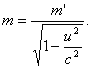
Умножим обе части соотношения (6) на с2 и обозначим mс2 = Е, m'с2 = Е'. Тогда получим:
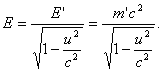
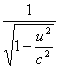
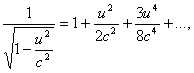
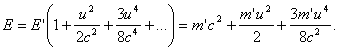
С увеличением скорости растет масса тела и, следовательно, его энергия. Соотношение (7) и выражает закон сохранения энергии. При любых процессах энергия любой замкнутой системы остается постоянной, хотя ее масса покоя может меняться. Например, если покоящееся тело массы М самопроизвольно распадается на два тела с массами М1, М2, разлетающихся со скоростями u1, u2, то будет иметь место соотношение:
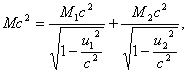
Заметим, что разность ДЛ/ = А/ — (М1-}-М^) называется дефектом массы.
Из соотношения (7) следует, что движение со скоростью света возможно лишь, если масса покоя m' = 0, поскольку энергия должна быть конечна. «Частицы» света — фотоны, скорость которых равна скорости света, имеют, следовательно, массу покоя, равную нулю. Из соотношения (7) также следует, что скорость света является предельно возможной скоростью движения (при u>с масса частиц становится мнимой).
Соотношения (1) — (3) являются справедливыми и в системе отсчета K, в релятивистском случае, если их написать в виде:
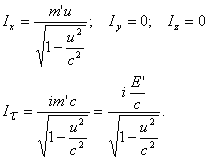
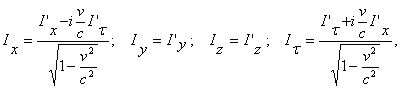
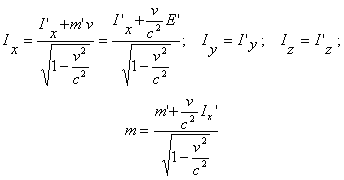
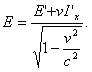
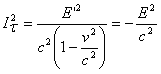
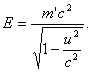
В системе отсчета К', где данное тело покоится, сила определяется, как в обычной классической механике.
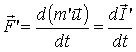
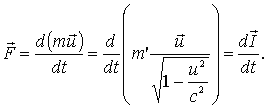
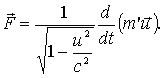
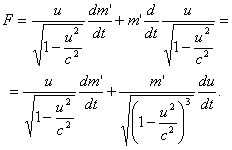
§ 3. Выведем теперь основные уравнения движения релятивистской ракеты.
Закон ее движения определяется следующим образом. Пусть в собственной системе отсчета К' за единицу времени через сопло ракеты выбрасывается со скоростью — а масса 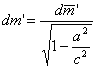 (где m' масса покоя).
(где m' масса покоя).
Тогда
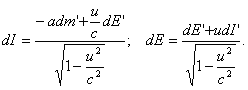
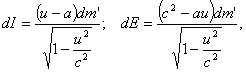
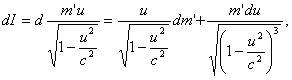
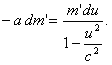
Интегрируя выражение (4) при условии, что t = 0; u = 0; m' = m'0(m'0 — начальная масса), придем к формуле:
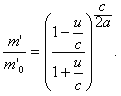
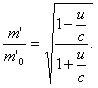

Из соотношения (5) следует, что только при а ≧ с (при значениях а, близких к с) получаются разумные отношения ![]() при а≪с эти отношения получаются исключительно маленькими; так, например, при а = 15 тыс. км/сек (скорость истечения из сопла мощной атомной ракеты) для достижения скорости u = (1 — 0,1)c = 0,9 с получаем, что
при а≪с эти отношения получаются исключительно маленькими; так, например, при а = 15 тыс. км/сек (скорость истечения из сопла мощной атомной ракеты) для достижения скорости u = (1 — 0,1)c = 0,9 с получаем, что
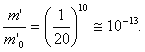
При а = с в данном случае ![]() , что вполне реально. Соотношение для dE не представляет для нас интереса, оно вспомогательное.
, что вполне реально. Соотношение для dE не представляет для нас интереса, оно вспомогательное.
Поскольку при различных ядерных реакциях часть энергии переходит в электромагнитное излучение, а часть содержится в различных образующихся и разлетающихся частицах, то соотношение (5) нужно несколько уточнить (даже при аннигиляции не вся энергия переходит в энергию электромагнитного излучения).
Пусть
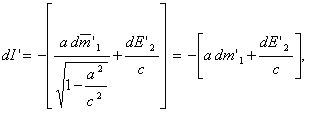
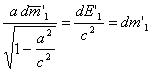
![]() — часть массы, переходящей в энергию электромагнитного излучения.
— часть массы, переходящей в энергию электромагнитного излучения.
Поскольку
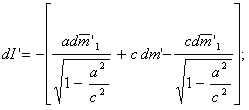
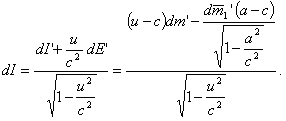
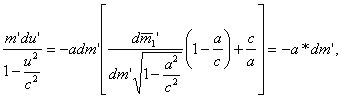
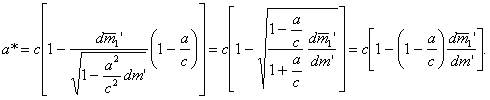
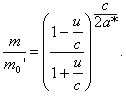
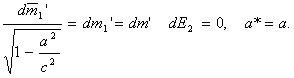
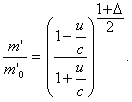
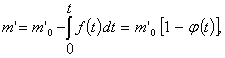
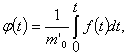
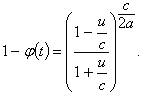
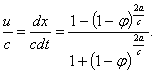
Зная связь собственного времени (t') с земным (t) в общем случае из выражения (13, § 1), найдем связь между u и t' и х и t'.
В частном случае равноускоренного движения имеем:
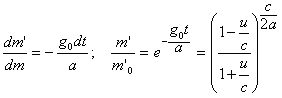
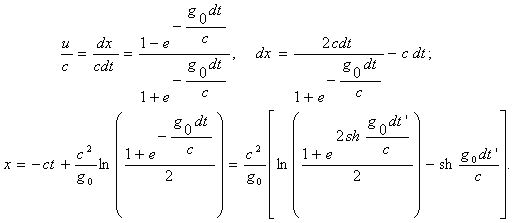
После прекращения выброса энергии через сопло в случае инерциального движения, поскольку
Имеем
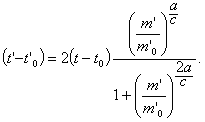
В случае непрямолинейных траекторий также можно без большого труда получить необходимые соотношения, использовав для этой цели общие соотношения между импульсом и силой. (В случае скоростей, весьма близких к скорости света, необходимо использование общей теории относительности, что однако пока не представляется необходимым).
§ 4. Вычислим, правда очень приблизительно, величину возможной плотности и скорости подачи вещества и антивещества в область аннигиляции в зависимости от расстояния, с которого происходит подача. При аннигиляции возникнет сильное излучение, давление которого будет стремиться удалить частицы вещества и антивещества от места их встречи.
Принципиально возможна подача как твердых частиц обоих веществ, так и подача их в виде газов. Однако более вероятен и целесообразен второй случай, когда антивещество, находясь в плазменном состоянии, может храниться окруженное магнитным полем без соприкосновения со стенками «хранилища».
Рассмотрим сначала именно этот случай. Как известно, для излучения абсолютно черного тела давление радиации (практически любых длин волн) определяется соотношением:
Таким образом,
Градиент давления, оказываемого радиацией на газообразную среду, учитывая ее реальные свойства вследствие поглощения радиации, равен
![]() — интегральное среднее значение так называемого коэффициента поглощения излучения (kν — коэффициент поглощения при заданной частоте излучения ν).
— интегральное среднее значение так называемого коэффициента поглощения излучения (kν — коэффициент поглощения при заданной частоте излучения ν).
Для сильно поглощающих сред kν имеет большое значение, для почти прозрачных сред kν мало, kν зависит от температуры и скорости среды (и обычно дается таблично). F — полный поток энергии. Fν — поток энергии излучения в интервале частот (ν, ν + dν ). k имеет размерность ![]() , где l — элемент длины.
, где l — элемент длины.
Поскольку уравнение движения каждой частицы газа можно написать в виде
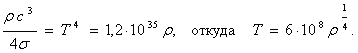
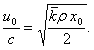
В случае твердых частиц сила светового давления, действующая на частицу, будет равна:
При аннигиляции, например, протона и антипротона образуются не только γ-кванты (электромагнитное излучение), но и различные частицы и, в частности, π±-мезоны, которые за время 2,5·10-8сек. распадаются на μ±-мезоны и нейтрино, а те в свою очередь через 2·10-6 сек. распадаются на β±-излучение (позитроны и электроны) и 2 нейтрино. При этом средний путь этих мезонов составляет сотни метров — километры. В других случаях образуются другие заряженные и нейтральные частицы.
Эти частицы проходят путь в сотни метров и километров, прежде чем полностью или частично превращаются в электромагнитное излучение. Траекторию этих частиц можно отключить (отразить) в сильном электромагнитном поле, которое будет играть роль «зеркала», и, таким образом, на «оптическое» зеркало попадает не очень значительная часть полной энергии и нейтральные частицы, процент которых от общего числа частиц невелик. В случае магнитного поля можно сделать следующую оценку.
Поскольку давление магнитного поля
Закон движения заряженной частицы под влиянием электромагнитного поля описывается уравнением:
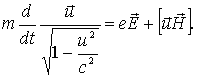
Например, в случае только электрического поля и прямолинейной траектории имеем:
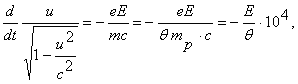
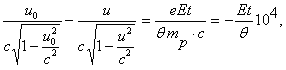
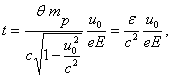
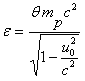 — энергия частицы. Для процесса аннигиляции характерна энергия частиц порядка 10-3 эрг = 6·108 эв = 600 мэв. Полагая u0 = с, придем к соотношению, определяющему Е:
— энергия частицы. Для процесса аннигиляции характерна энергия частиц порядка 10-3 эрг = 6·108 эв = 600 мэв. Полагая u0 = с, придем к соотношению, определяющему Е:
Комбинированное действие электрического и магнитного поля сделает результат «отражения» еще более надежным и при меньших расстояниях, проходимых частицами. Создание сильных электромагнитных полей в больших объемах будет, несомненно, возможно при постройке фотонных ракет. Сравнительно небольшая часть энергии «двигателей» вполне может быть использована для этой цели.