III

От микромира в космос

Достижимые скорости
и время межзвездного путешествия

П

Попробуем также предугадать способы обеспечения энергетических потребностей звездолетов.

Как уже отмечалось, звездолеты — аппараты, для которых в обозримом будущем, по-видимому, будет характерна незначительная величина абсолютной тяги по сравнению с их массой (весом). Ясно, однако, что чем меньше тяга, тем медленнее будет разгоняться звездолет, и время, которое будет затрачено на путешествие, может стать чересчур продолжительным. С другой стороны, наибольшее значение тяги двигателя ограничивается, в частности, тем обстоятельством, что, хотя с ростом тяги сокращается время путешествия, на участке, который можно преодолеть за приемлемое время и без достижения самых больших скоростей, становятся чрезмерными необходимые запасы горючего.

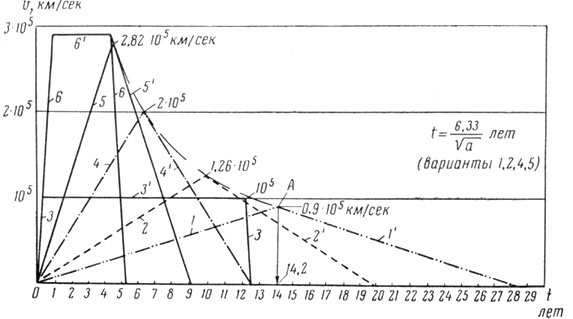Рис. 18. Некоторые схемы полетов к Проксима Центавра 1-1' — схема полета «минимального» звездолета при а = 0,2 м/сек2; 2-2' — а = =0,4 м/сек2 с постоянно-работающим двигателем; 3-3'-3-а = g= 9,81 м/сек2 до vК=105 км/сек с последующим выключением двигателя и новым включением для торможения; 4 — 4' — а = 1 м/сек2 с постоянно работающим двигателем; 5-5'-а=2 м/сек2 с постоянно работающим двигателем; 6-6'-6 — а = g = 9,81 м/сек2 до vК=2,9·105 км/сек с выключением двигателя и новым включением для торможения

Примем, что ускорение составляет 0,2 м/сек², для чего тяга двигателя должна составлять примерно ¹/₅₀ собственной массы звездолета.

Программой полета предусматривается, что разгон продолжается до половины пути с последующим торможением на второй его части, а значит двигатель работает непрерывно (рис. 18, траектория 1-1'). В этом случае возможна сравнительно несложная оценка времени, необходимого для полета, например, к Проксима Центавра с возвращением в Солнечную систему.

Как известно, пройденный путь при равноускоренном движении выражается простой зависимостью:

(3.1)

t — время, сек.
Отсюда время полета до половины пути с разгоном (3-2)

Расстояние до Проксима Центавра составляет 4,27 световых лет (напомним, что свет проходит за год 9,36 · 10¹² км). Половина этого расстояния (до точки А), преодолеваемая с разгоном, равна 2·10¹⁶ м, или 2·10¹³ км (20 триллионов км). Тогда время полета с разгоном составит:

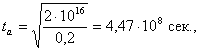
Наибольшая скорость, которая будет получена к моменту окончания разгона:

v_к = at_a = 0,2 · 4,47·10⁸ = 9 · 10⁴ км/сек. (3.3)

Характер работы двигателя	Траектория на рис. 18	Ускорение, м/сек2	Наибольшая достигнутая скорость, vк км/'сек	Время путешествия для экипажа te годы	Необходимый запас массы покоя на каждые 100 т·сек2/м стартовой массы, т·сек2/м
Двигатель работает непрерывно	1-1' 2-2' 3-3' 4-4'	0,2 0,4 1,0 2,0	0,9·105 1,26·105 2·105 2,82·105	56,8 40,0 25,3 18,2	20 23 48 83	0,8 0,77 0,52 0,16	0,290 0,164 0,023 0,007
Двигатель работает часть времени	3-3'-3 6-6'-6	9,81 9,81	105 2,9·105	26,1 10,6	10,5 η0,5=103 η0,52=99,2 η0,55=93,8 η0,6=86,0	0,77 0,008 0,062 0,14	0,160 0,00036

Аналогично определяется время межзвездного путешествия, если предположить ряд других постоянных ускорений: а = 0,4 м/сек², а = 1 м/сек², а = 2 м/сек² (см. рис. 18, траектории 2 — 2', 4 — 4' и 5 — 5'). Результаты этих расчетов сведены в табл. 3.

Предположим далее, что возможное постоянное ускорение составляет 9,81 м/сек², т. е. тяга аппарата равна его массе. По всей вероятности, достижение такого отношения тяги к массе невозможно в сколько-нибудь обозримом будущем, так как предлагавшиеся до сих пор двигатели галактических кораблей в их осуществимых вариантах — двигатели принципиально малых тяг. Если ракета с ускорением 9,81 м/сек² разгоняется до 10⁵ км/сек (см. рис. 18, траектория 3 — 3'— 3), затем часть пути летит с выключенным двигателем (участок 3') и вновь включает его для торможения перед входом в планетную систему Проксима Центавра, то время разгона до скорости 10⁵ км/сек составит

Следовательно, на разгон и торможение будет затрачено при полете в одном направлении примерно 0,64 года. За время одного разгона, либо торможения, ракетой будет пройден путь:

Оставшийся путь L_vconst = L — 2L_a = 400 ·10¹⁴ — 9,81·10¹⁴ — 3,9·10¹⁶ м будет пройден со скоростью v_const = 10⁵ км/сек = 10⁸ м/сек за время:

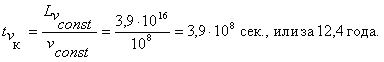
Таким образом, полет в один конец займет всего 12,4 + 0,64 = 13 лет, а на все путешествие должно быть затрачено 26 лет (см. рис. 18, траектория 3 — 3' — 3). Аналогично выполняется расчет при том же ускорении и разгоне до 2,9 -10⁵ км/сек (траектория 6 — 6'— 6).

Однако, поскольку в этом случае скорость полета близка к скорости света, при оценке срока путешествия для земного наблюдателя необходимо учесть изменение хода времени на Земле (t₀) по сравнению с временем, проходящим для путешественников в ракете (t_e). К этой b другим особенностям полетов на околосветовых скоростях мы еще вернемся, чтобы рассказать о них подробнее.

Для определения наименьшей возможной продолжительности путешествия следует естественно оценить наибольшую скорость, которая при определенных условиях может быть достигнута галактическим кораблем. Прежде всего напомним, что создание ракеты, летающей со скоростью, равной скорости света, либо превышающей ее, абсолютно невозможно. Ведь только в том случае, когда вся масса некоторого тела превращается в электромагнитное излучение, в кванты, может достигаться световая скорость. Поскольку для корабля остается масса его конструкции, экипажа, груза, световая скорость не может быть им достигнута. Это становится еще более очевидным, если мы вспомним, что звездолетный аппарат предназначается не просто для достижения максимальной скорости, возможной в нашем мире, а в качестве транспортного средства. Разгон и торможение на пути к другому миру и снова разгон и торможение на обратном пути — обязательные элементы его траектории.

Сказанное означает, что на двукратный разгон до скорости света и на двукратное фактически полное торможение понадобилось бы полных четыре массы покоя (собственных масс) звездолета. Принципиальная неразрешимость этой задачи совершенно очевидна. На сколько же может приблизиться скорость квантового корабля к скорости света? Чтобы ответить на этот вопрос, воспользуемся обобщенным уравнением К. Э. Циолковского¹, которое может быть использовано в случае, когда аппарат движется со скоростью порядка скорости света. Это уравнение (полученное в приведенном виде наиболее простым способом проф. К. П. Станюковичем) понадобится нам в дальнейшем.

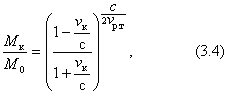
с — скорость света;

v_p.т— скорость истечения рабочего тела (для электромагнитной ракеты при v_р.т= с степень выражения, стоящего в скобках, будет равна ½).

¹ В частном случае, когда скорость полета и скорость истечения существенно меньше скорости света, из этого уравнения разложением в ряд и последующим суммированием можно получить формулу К. Э. Циолковского для полетов с относительно малыми скоростями.

Важно отметить, что, подставив в уравнение (3,4) зависимость, позволяющую найти Лоренцево сокращение времени, после простых преобразований получаем выражение, связывающее интервалы времени, проходящие на Земле t₀ и в звездолете t_e:

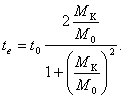
Из этого выражения видно, что когда конечная масса аппарата М_к по сравнению со стартовой не изменяется, на нем проходят те же интервалы времени, что и на Земле. Для того чтобы время на аппарате «остановилось», что характерно для движения со скоростью света, надо, чтобы т. е. необходимо полное излучение массы покоя звездолета. Приведенное рассуждение еще раз подтверждает, что скорость звездолета не может сравняться со скоростью света.

Итак, принимая скорость истечения рабочего тела из сопла двигателя ракеты равной скорости света 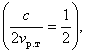и подставляя в уравнение (3.4) ряд отношений масс отвечающих случаю одного набора скорости (одного разгона) при равноускоренном движении, получим соответствующие каждому из них наибольшие достижимые скорости движения v_к (рис. 19, кривая I). Для звездного корабля за время путешествия с возвращением можно считать обязательным разгон с последующим торможением на пути к цели и снова разгон с последующим торможением на обратном пути. В каждом таком случае разгоняющаяся или тормозящаяся (отрицательное ускорение) ступень корабля для получения необходимой конечной скорости при достигнутой постоянной скорости истечения рабочего тела должна иметь определенное отношение масс.

Поскольку необходимо преодолеть четыре таких участка, следует учетверить отношение масс, т. е. определить величину отношения 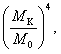которое и будет показывать отношение масс для всего корабля от момента старта из Солнечной системы до момента возвращения в нее.

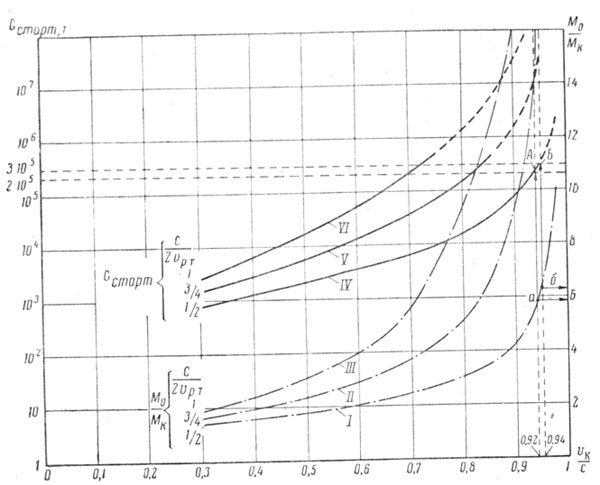Рис. 19. Зависимость отношения масс для четырехступенчатого галактического корабля и его стартового «земного» веса (при возвращаемом весе 200 т) от наибольшей скорости Зависимости получены для ряда скоростей истечения (параметр ) при «балластировании» реакции аннигиляции

Таким образом, в рассмотренном случае, когда , для достижения конечной скорости v_к, отвечающей 0,94 % от скорости электромагнитного излучения (света), нужно на каждом из этапов разгона или торможения обеспечить отношение масс, отмеченное точкой а, т. е. Условившись, что для галактического корабля такое отношение масс (близкое к отношению масс для современных одноступенчатых химических ракет) удастся обеспечить в одной ступени, приходим к выводу, что ракета должна состоять из четырех ступеней и, кроме того, в ее головной части необходимо разместить грузы, продовольствие, снаряжение и экипаж. Тогда общее отношение масс для нее составит 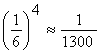. Лишь столь ничтожная часть первоначально стартовавшей массы корабля вернется в систему Солнца, проделав путь сквозь бездны космоса.

Результаты расчетов для сведены в табл. 4.

Таблица 4

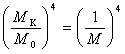		vк, тыс. км/сек
⅓		240,0	0,800
		272,3	0,905
		277,0	0,925
		283,3	0,945
		285,3	0,955
		293,8	0,980

Чтобы дать представление не об относительной, а об абсолютной массе корабля, стартующего на наибольшую технически представимую сегодня дальность, на рис. 19 приведены кривые IV — VI, показывающие зависимость начального веса (массы) четырехступенчатого галактического корабля от того значения которое должно быть достигнуто. Эти кривые нанесены в предположении, что при возвращении в Солнечную систему последняя ступень звездолета с экипажем, аварийными запасами и оставшимся снаряжением будет иметь на Земле вес всего 200 т ¹. Как видно из графика, даже при v_р.т = с (точка А) для достижения 94% от скорости света вес звездолета при старте должен составлять около 210 тыс. т, а при 95% от скорости света (точка Б) уже 300 тыс. т! Последний стартовый вес, вероятно, можно считать уже неприемлемым. Таким образом, в технически обозримом будущем максимальная скорость звездолетов едва ли превысит 90 — 94% от скорости света.

¹ Эта цифра представляется минимально вероятной, если принять, что после того, как звездолет стал спутником другой звезды и имевшаяся на нем малая вспомогательная ракета для полетов экипажа на планеты выполнила свои задачи, она не берется в обратный рейс. Возвращение экипажа на Землю с последней ступени, пришедшей в Солнечную систему, должно осуществляться обычными межпланетными ракетами.

Энергетические потребности
и «топливо» галактических кораблей

Рассмотрим конкретный пример.

Предположим, что звездный корабль имеет при старте массу М₀ = 100 т·сек²/м = 10⁵ кг·сек²/м, что отвечает земному весу G = 9,81·10² т, т. е. всего около 1000 т¹. Это примерно вес половины обычного груженого железнодорожного состава.

¹ Поскольку звездолет должен стартовать, например, с орбиты, где он до этого находился на положении спутника, т. е. в состоянии невесомости, термин «вес» используется, чтобы получить земное представление о масштабах корабля, а также о весе конструкции, которые, возможно, придется доставить с Земли для его сборки в космическом пространстве. Масса М выражается в технической системе единиц (MKS).

Наши ориентировочные расчеты могут, естественно, относиться и к каждой тысяче тонн земного веса звездолета, весящего в действительности в любое число раз больше.

Предположим, что постоянное ускорение аппарата а = 0,2 м/сек². Примем также при первоначальной очень грубой оценке, что дополнительное возрастание скорости вследствие неизбежного уменьшения массы аппарата в связи с ее расходованием за время разгона относится в запас расчета (например, в запас, нужный для совершения маневров, обеспечения безопасности и пр.). Тогда, согласно известной зависимости, постоянная тяга, создаваемая двигателем, должна составлять:

Если принять далее, что двигатель работает, создавая постоянную тягу, в течение всего времени путешествия к Проксима Центавра и обратно, то суммарный расход энергии (тепла) составит:

Энергетические возможности всех химических горючих ископаемых Земли оцениваются примерно в 23,5 · 10¹⁵квт-ч, или E_т = 20,4 10¹⁸ ккал. Следовательно, вычисленное необходимое количество энергии составляет более ¹/₅ всех энергетических запасов химического топлива, разведанного на Земле (и то лишь на 1000 т земного веса корабля при старте).

Если предположить, что в качестве горючего для галактического корабля используется такое широко известное ракетное химическое топливо как смесь спирта с кислородом (1 кг такой смеси отдает при сгорании примерно 2·10³ ккал), то, принимая коэффициент полезного действия источника энергии η_дв = 0,5, можно оценить весовой запас химического топлива, которое должно быть доставлено с Земли на звездолет:

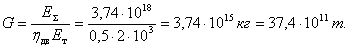
Полученный вес необходимого топлива в 38·10⁸ раз превышает принятый в начале расчета стартовый вес всего галактического корабля и поэтому не может быть взят на борт.

При удельном весе смеси примерно γ = 1 т/м³ объем необходимого топлива составит 3800 км³. Такой объем воды Волга выносит в море примерно за 150 лет. А поскольку, как отмечалось выше, полет при ускорении 0,2 м/сек² должен продолжаться (в оба конца) около 50 лет, значит, что все это время в камеру сгорания ракеты должна непрерывно поступать река топлива втрое полноводнее Волги. Шар, вмещающий такое количество жидкости (в действительности указанные составляющие смеси пришлось бы хранить в отдельных баках), имел бы диаметр почти 20 км.

При том же коэффициенте полезного действия необходимый запас ядерного горючего, например U-235, был бы значительно меньшим, так как 1 кг его может дать около 20 млн. квт-ч, или 1,96·10¹⁰ ккал. Запасы ядерного горючего, далеко не полностью учтенные, определяются цифрой 519·10¹⁵ квт-ч, т. е. они примерно в 22 раза превышают энергетические запасы химического топлива.

Потребный весовой запас U-235, имеющего «калорийность» E_т = 1,96·10¹⁰ ккал/кг при к. п. д. источника энергии η= 0,5, составит в земном весе 3,8-10⁵ т.

Как видно, и в этом случае вес необходимого запаса горючего примерно в 400 раз превышает вес звездолета, принятый при расчете за исходный, т. е. примерно во столько же раз, во сколько яблоко тяжелее своего семени. Необходимый объем металлического U-235, имеющего удельный вес γ = 18,7 т/м³, составит «всего»

Бак для ядерного горючего в этом случае должен представлять собой шар диаметром 33,7 м (с соответствующими изолирующими перегородками между отдельными частями горючего для предотвращения взрывной цепной реакции). Совершенно ясно, что ядерное горючее не может обеспечить энергетических потребностей звездолета.

Оценим возможность обеспечения потребностей звездолета за счет использования энергии, получаемой в ходе термоядерной реакции в результате синтеза легких элементов, когда происходит слияние двух легких ядер в одно более тяжелое ядро. Одним из легких элементов, которые можно использовать в этом процессе, является изотоп водорода — дейтерий.

Поскольку из единицы веса исходного сырья при термоядерной реакции принципиально возможно получение примерно в 8 раз большего количества энергии, чем при использовании единицы ядерного горючего U-235, потребный весовой запас горючего может быть соответственно уменьшен до 4,67·10⁴ т, т. е. даже в этом случае необходимый весовой запас топлива почти в 50 раз превышает принятый вес звездолета.

Предположив, что удельный вес горючего γ = 2 т/м³, получим, что необходимый объем баков составляет 2,23·10⁴ м³. Бак, вмещающий такое количество дейтерия, должен иметь диаметр 35 м. Любопытно, что в этом случае объем бака для размещения исходного сырья, необходимого для термоядерной реакции, почти не изменился по сравнению с размерами бака для U-235 из-за низкого удельного веса дейтерия по сравнению с U-235. Поскольку, как было показано, весовой запас исходного сырья для получения термоядерной энергии в количестве, необходимом для обеспечения минимального межзвездного полета, также в 50 раз больше стартового веса звездолета, придется отказаться от использования и этого «топлива».

Наконец, обратимся к возможностям использования предполагаемой реакции, о которой мы уже упоминали, реакции, в ходе которой масса покоя вещества полностью излучается.

Еще в 1871 г. Д. И. Менделеев (1834— 1907) утверждал, что масса атома не обязательно должна равняться сумме масс составляющих его частиц. По разнице между массой частиц и массой образованных атомов, в частности, судят об энергии, выделяющейся в ходе ядерных реакций.

На пути увеличения выхода энергии из вещества физика наших дней совершает лишь первые шаги. Известно, что при цепной реакции на ядрах U-235 в световое излучение превращается лишь ¹/₁₀₀₀ доля массы, участвовавшей в реакции. Всего около ¹/₁₀₀ составляет убывание (дефект) массы термоядерной реакции, за счет которой выделяется энергия Солнца. Но представим себе, что сложнейшая проблема полного превращения массы покоя в свет решена. Тогда, согласно соотношению

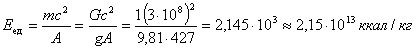
Как видно, энергоемкость единицы массы покоя в 10¹⁰ раз больше, чем у единицы самой высокосортной горючей химической смеси. Таковы удивительные возможности горючего «наивысшей калорийности».

Учитывая часть энергии, используемой для создания тяги звездолета, с помощью коэффициента η = 0,5, который принимался и ранее, оценим расход массы покоя на каждые 100 т·сек²/м массы звездного корабля при полете от Земли к Проксима Центавра:

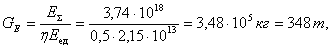
Все предыдущие расчеты не нуждались в уточнении, поскольку потребное количество «топлива» многократно превышало собственный — стартовый вес аппарата. А это означало, что оно принципиально не может быть использовано даже и в варианте многоступенчатой ракеты, ибо ясно, что аппарат не может весить больше самого себя. Поэтому ранее рассмотренные варианты были заведомо неосуществимыми.

В последнем же случае, когда масса аппарата и запасы массы покоя, необходимые для обеспечения его энергетических нужд, оказались соизмеримыми, следует уточнить расход массы покоя. Естественно, что он будет меньшим, чем предварительно вычисленный, в связи с тем, что масса разгоняемого аппарата будет уменьшаться от начала до конца пути по мере выработки «топлива» и сбрасывания промежуточных ступеней.

Воспользуемся обобщенным уравнением Циолковского. Подставляя в него вычисленную выше максимальную скорость, которая может быть достигнута при ускорении 0,2 м/сек² за время преодоления половины расстояния в конце первого участка разгона, получим при v_{р. т} =с (для электромагнитной ракеты скорость истечения рабочего тела — электромагнитных волн — равна скорости света):

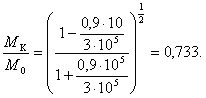
Условимся, что ускорение на всем протяжении полета остается постоянным (см. рис. 18, траектория 1-1') и лишь четыре раза меняется по знаку по мере выработки «топлива». Поэтому с уменьшением массы звездолета в связи с расходованием «топлива» и отбрасыванием частей ракеты будут также соответственно уменьшаться как потребная тяга двигателя, так и расход рабочего тела. В расчете первого приближения это обстоятельство не учитывалось, так как ставилась задача определить лишь порядок величины расхода горючего.

Осредненные значения массы звездолета и соответственно тяги его двигателя в характерных точках по траектории всего полета нетрудно вычислить, воспользовавшись найденным значением и отношением массы к тяге, необходимым для получения принятого ускорения.

Ракета дважды разгоняется, и дважды тормозится.В каждом из этих случаев понадобится обеспечить отношение масс = 0,733, вычисленное выше, т. е. для всего полета в оба конца 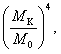= 0,733⁴~ 0,29 (напомним, что столь небольшое отношение масс объясняется тем, что предполагаемая скорость истечения рабочего тела равна скорости света).

Известно, что потребная тяга связана с массой и ускорением простым соотношением:

(3.5)

Поскольку а = const и масса аппарата по времени изменяется линейно, то и тяга будет изменяться линейно, т. е.

F = M₀ — kt,(3.6)

(М' — масса аппарата в конце участка, для которого определяется средняя тяга).

Следовательно, средняя тяга, необходимая для определения запасов рабочего тела, «топлива», может быть определена из уравнения:

Принимая на каждом из участков F_ср (относимое при вычислении запаса горючего для аппарата ко всему участку) равным полусумме потребных тяг на его концах, получим, например на участке 1 (см. рис. 18), т. е. при разгоне на первой половине пути к Проксима Центавра, необходимый расход энергии на каждые 100 т·сек²/м стартовавшей массы ракеты:

Аналогично вычисляются затраты массы покоя на остальных участках траектории (табл. 5).

Таблица 5

Окончательно потребное количество массы покоя при ее использовании с к.п.д. η = 0,5 при движении по траектории 1 — 1' составит:

Таким образом, запас массы покоя, необходимый для обеспечения энергетических потребностей «минимального» звездолета при использовании всего запаса внутренней энергии вещества, представляется приемлемым. Если иметь в виду, что не исключена возможность хотя бы частичного набора «топлива» — расходуемой массы покоя, необходимой для обратного путешествия, на достигнутой планете, можно считать, что решение задачи дополнительно облегчается.

Аналогично вычисляются затраты массы покоя при разгонах с другими ускорениями и вариантами траекторий, показанными на рис. 18, отвечающими как случаям работы двигателя в течение всего времени путешествия, так и таким, когда после разгона до некоторой скорости галактический корабль часть пути преодолевает с выключенным двигателем, а затем вновь включает его для торможения.

Результаты расчетов внесены в табл. 3.

Следует отметить, что определение запасов массы покоя, необходимых для обеспечения движения по траектории 6—6'—6, показало, что даже при использовании полной энергии вещества для получения тяги с коэффициентом преобразования η = 0,5 расходуемая масса покоя должна быть больше стартовой (М_т = 103 т·сек²/м), что обеспечить невозможно. Только при условии возрастания к.п.д. преобразования энергии в тягу до η = 0,52 и выше появится возможность обеспечить энергетические потребности галактического корабля, разгоняющегося с ускорением а = 9,8 м/сек² до скорости v = 2,9·10⁵ км/сек.

Чтобы представить себе, как велико наименьшее количество энергии, потребное для этого полета, достаточно сказать, что за двадцать последних веков человечество использовало для своих нужд столько энергии, сколько можно получить при аннигиляции половины массы ионов (10 т·сек²/м), необходимой для полета «минимального» звездолета к Проксима Центавра.

Итак, только проникновение в самые сокровенные глубины материи, овладение процессами получения энергии за счет излучения массы покоя вещества, проникновение в тайны микромира открывает человеку путь к самым крупным материальным системам — другим звездным мирам и галактикам. От микромира в макрокосмос — таков единый поток человеческого познания.

Можно ли использовать для звездолета
ионный двигатель!

Уточним возможность использования ионного двигателя для галактического корабля и, в частности, для звездного путешествия минимальной протяженности — к Проксима Центавра. Это позволит нам одновременно выявить некоторые характеристики и особенности ионолета.

Предположим первоначально, что скорость истечения рабочего тела из сопел двигателя аппарата весьма высока: v_{р. т} = 5·10⁴ км/сек¹, т. е. ¹/₆ от скорости света. Этого условия достаточно, чтобы оценить отношение масс и наименьшее число ступеней, при которых может быть достигнута минимальная необходимая скорость звездолета в конце участка разгона, позволяющая, как было показано выше, совершить межзвездное путешествие за срок жизни человека и равная 10⁵ км/сек ². Воспользовавшись для самой предварительной оценки классическим уравнением К. Э. Циолковского [уравнение (2.7)] и подставив в него известные величины — скорость истечения и конечную скорость полета (в конце участка разгона), получим, что на каждом из участков разгона или торможения потребуется обеспечить отношение масс:

¹ Эти и еще более высокие скорости истечения «тяжелых» ионов в практически значительном количестве для создания тяги пока неосуществимы и принимаются лишь для принципиальной оценки возможностей ионного двигателя.

² В случае, рассмотренном ранее и представленном на рис. 18 (траектория 1-1'), скорость v_к = 9·10⁴ км/сек. В настоящем приближенном расчете для упрощения принимается v_к = 10⁵ км/сек, а срок полета сохраняется прежним. Принятое изменение V_к не может заметно сказаться на конечных результатах расчета.

Как уже отмечалось, для реальных конструкций отношение масс для одной ступени ракеты в наши дни лежит в интервале 3,5—10. Принимая его равным 7,5, получим, что при скорости рабочего тела v_{р .т} = 5·10⁴ км/сек для всего полета по маршруту от Солнечной системы до системы Проксима Центавра и обратно, т. е. на два разгона и два торможения, понадобится по крайней мере четырехступенчатый аппарат.

Используя для уточнения приведенной выше оценки уравнение К. Э. Циолковского в форме, описывающей случай движения с околосветовой скоростью [уравнение (3.4)], получим для любого из участков разгона или торможения уточненное обратное отношение масс , т. е. лишь на 6% меньшее, чем вычисленное прежде по уравнению (2,7).

Как видно, даже при скорости полета, достигающей ⅓ скорости света, еще не происходит принципиального изменения потребного соотношения масс по сравнению с вычисленным по классической формуле.

Итак, вычисленное значение . Следовательно, к моменту завершения каждого очередного разгона, либо торможения масса звездолета должна уменьшиться в 8 раз по сравнению с той, которую корабль имел в начале этого участка. В результате масса звездолета на всем протяжении рейса должна изменяться, как показано на рис. 20. Последовательно должны сбрасываться три ступени, и лишь груз четвертой может возвратиться к месту старта. Таким образом, к месту старта возвращается 0,125⁴, т. е. примерно лишь ²/₁₀₀₀₀ от стартовавшей массы корабля, в то время как для квантовой ракеты с той же наибольшей скоростью в Солнечную систему вернулась бы почти ⅓ стартовавшей массы. По-прежнему предполагается, что энергетические потребности двигателя обеспечиваются в результате использования энергии, полученной за счет излучения массы покоя. Кроме того, как и раньше, принимается, что лишь половину выделившейся из вещества энергии удается использовать для ионизации и разгона рабочего тела.

Расход массы покоя на обеспечение энергетических нужд звездолета на участке разгона 0—I составит

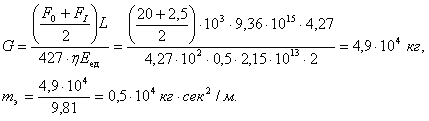
Напомним, однако, что в рассматриваемом варианте двигателя вычисленная масса покоя, взятая на борт летательного аппарата и служащая лишь источником энергии, не используется непосредственно для отбрасывания, для получения реактивной тяги. Реактивный эффект должен создаваться за счет отбрасывания струи предварительно разогнанных атомов и молекул некоторого вещества, дополнительно взятого на борт. Поэтому необходимо оценить потребный запас также и этого рабочего тела.

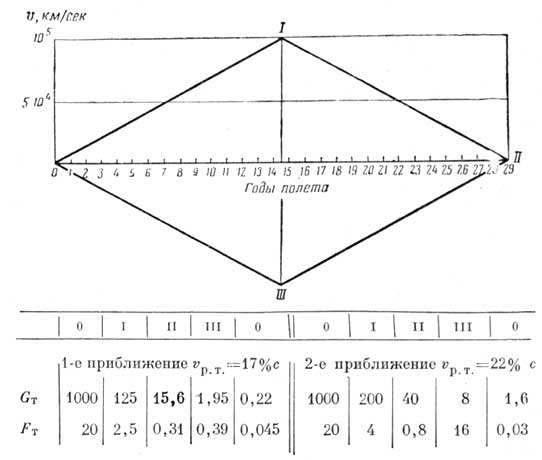Рис. 20. К возможностям использования ионного двигателя для звездолета. Схема движения ионолета (в таблице представлено изменение «земного веса» Gт и тяги Fт в характерных точках на схеме)

По мере использования «топлива» и рабочего тела, а также сбрасывания излишних частей конструкции будет уменьшаться и тяга, необходимая для получения постоянного ускорения а = 0,2 м/сек². Значения потребной тяги в конце каждого участка разгона и торможения приведены на рис. 20 (первое приближение).

Масса «топлива», расходуемого на первом участке (участок 0—I), оценивается с использованием простой зависимости:

(3.8)

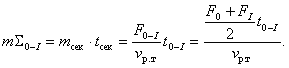
Подставляя в последнюю зависимость известные исходные данные и, в частности, время работы двигателя на участке 0—1, оцененное ранее и равное 14,2 года, получим:

Вся масса рабочего тела и массы покоя, служащая для обеспечения энергетических потребностей звездного корабля, составит:

Как видно, потребная масса рабочего тела получилась большей, чем стартовая масса аппарата, взятая за исходную при расчете 100 т·сек²/м. Это значит, что при скорости истечения рабочего тела, принятой выше, создание такого звездолета невозможно.

Обратимся к определению наименьшей скорости истечения рабочего тела, при которой принципиально может быть обеспечено создание «минимального» звездного ионолета.

В конце участка 0— I, как было установлено, масса ступени должна уменьшиться с 10⁵ до 0, 125·10⁵ кг·сек²/м. Тогда, если принять, что масса конструкции ступени М_к составляет ¹/₇ от массы вмещающегося в нее рабочего тела и горючего М_Е, получим возможную массу М_В отбрасываемого рабочего тела:

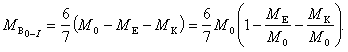
Подставляя известные величины, получим:

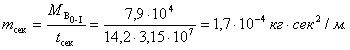
Как видно, v_р.т должна быть очень большой и составлять не менее 22% от скорости света.

В результате расчета второго приближения с введением в обобщенное уравнение К. Э. Циолковского вычисленного значения v_р.т = 6,6·10⁴ км/сек получим отношение масс в каждой ступени

Таким образом, отношение конечной массы звездолета к начальной его массе с учетом двух разгонов и торможений даже при минимальном приемлемом ускорении а = 0,2 м/сек составит:

В то же время для квантовой ракеты при том же времени путешествия отношение масс стартовой к конечной почти в 100 раз больше. С другой стороны, минимальная квантовая ракета с таким же отношением масс, какое нами определено для минимальной ионной ракеты (см. табл. 3), могла бы достичь скорости, равной 0,96 с, т. е. в 3 раза большей, чем ионная ракета.

Если принять, что вес кабины корабля вместе с экипажем, продовольствием и научным оборудованием ионного аппарата может составлять всего 20 т·сек²/м (около 200 т «земного» веса), получим, что масса ионолета при старте с орбиты спутника должна быть около 7500 т·сек²/м. А это значит, что вес грузов, доставленных с Земли к месту сборки звездолета, должен составлять около 740 тыс. т.

Столь грандиозный исходный вес ионолета, который сможет решить лишь первую задачу — осуществить путешествие к Проксима Центавра и к тому же при условии трудно достижимой скорости рабочего тела, свидетельствует о том, что ионный аппарат значительно менее перспективен для звездных полетов, чем «чисто электромагнитный» — квантовый, для которого при тех же ускорениях можно уложиться в существенно меньший стартовый вес, либо добиться больших ускорений при стартовом весе, равном весу минимального ионолета.

В заключение следует упомянуть, что возможности ионолета несколько расширятся в случае, если удастся использовать в качестве дополнительного рабочего тела инертной отбрасываемой массы — дополнительно разгоняемые частицы межзвездного газа или отбрасывать часть рабочего тела, имеющегося на борту, через сопло-эжектор с подсасыванием частиц межзвездного газа для увеличения отбрасываемой массы и, в конечном итоге, некоторого увеличения тяги при прежнем крайне ограниченном запасе инертной массы на борту аппарата.

Поскольку ионные двигатели, вероятно, будут широко применяться для полетов в пределах Солнечной системы, возможны и попытки их использования для звездолетных аппаратов. Однако, как было показано, при этом неизбежно встретятся затруднения, которые, по всей вероятности, заставят сосредоточить все усилия на создании квантолетов.

Межзвездная среда —
опасность или источник энергии?

Опасения столкновений космического корабля с метеоритами, которые прежде считались одной из главных преград для космических путешественников, оказались чрезмерными. В этом позволили убедиться эксперименты, поставленные на первых искусственных спутниках Земли и первой советской космической ракете. Во всяком случае, по-видимому, лишь один из небольших американских искусственных спутников был преждевременно выведен из строя из-за столкновения с метеоритами или метеорной пылью.

Но не часы или месяцы, а многие годы, десятилетия, и при том со скоростью, доходящей по крайней мере до 100 тыс. км/сек, будут мчаться ракеты среди звезд. Естественно, что прежде всего им предстоит преодолеть пространства Солнечной системы.

За последнее время сильно изменились представления о характере межпланетного газа. Совсем недавно его плотность считалась ничтожной. Предполагалось, что на каждый кубический сантиметр газа приходится лишь несколько частиц. Ныне высказывается предположение о том, что в межпланетном пространстве нет сплошной, равномерно распределенной газовой среды. Его пронизывают отдельые потоки сильно ионизированного газа, состоящие из электронов и протонов, выбрасываемые с поверхности Солнца и текущие со скоростью нескольких тысяч километров в секунду, потоки межпланетной плазмы. Много нового дали в изучении межпланетного газа искусственные спутники Земли. Эти сведения важны не только для межпланетных, но и для межзвездных полетов, тем более что и межпланетные ракеты смогут, хотя и неглубоко (за время жизни одного поколения), проникать в межзвездное пространство околосолнечной системы.

Можно провести некоторую аналогию между ракетой на химическом топливе, которая, пронизывая земную атмосферу, уносится в межпланетное пространство, и галактическим кораблем, покидающим внеземную станцию — спутник. Для такого корабля межпланетный газ и будет той первой «атмосферой», пронизав которую, он уйдет в межзвездное пространство. Так же как атмосфера Земли, следы которой имеются до высоты нескольких тысяч километров, по сравнению с протяжением межпланетного путешествия не больше, чем, например, пленка нефти на поверхности глубокой реки, так и межпланетный газ, заполняющий нашу Солнечную систему, не более чем молекулярная пленка на поверхности океана — межзвездного пространства, которое будут пересекать галактические корабли.

Будем надеяться, что опыт, накопленный в ходе межпланетных полетов, поможет галактическому кораблю преодолеть пространство Солнечной системы (как при старте, так и при его возвращении в нее), тем более, что на этих этапах его скорость будет еще относительно небольшой — ведь звездолет только начнет разгоняться или уже значительно затормозится. Наконец, можно представить себе, что старт галактического корабля осуществляется из района крайней планеты Солнечной системы, например Плутона. Вместе с тем можно предположить, что задача возвращения — обратного входа в систему Солнца или в планетную систему другой звезды — будет осуществляться для галактического корабля (так же как теперь задача возвращения искусственных спутников и космических кораблей на Землю) с неменьшими трудностями, чем старт. Однако несомненно, что главные и неизведанные опасности, все своеобразие и особенности которых сейчас еще трудно предвидеть, ожидают галактические корабли в самом межзвездном пространстве.

Важно также выяснить, существует ли возможность использования межзвездной материи для снабжения галактического корабля массой покоя, обеспечивающей его энергетические потребности.

При нашем приближенном рассмотрении мы не будем принимать во внимание собственную скорость межзвездного газа, которая весьма мала но сравнению со скоростью аппарата. Кроме того, поскольку, как уже отмечалось, в обозримом будущем технически можно рассчитывать на достижение собственных скоростей лишь одного порядка со скоростью света, мы ограничимся пока рассмотрением этой области скоростей полета¹.

¹ Некоторые вопросы, связанные с полетами на больших околосветовых скоростях и собственных очень высоких скоростях, изложены ниже.

С чем же будут сталкиваться, или взаимодействовать, галактические корабли на своем пути? Какие опасности их ожидают? Попробуем ответить на этот вопрос.

Исследования последних лет¹ показывают, что пространство, которое должны пересечь звездолеты, заполнено реальным веществом — межзвездной средой, а также электромагнитными излучениями и гравитационными полями. Из всей массы нашей Галактики, составляющей примерно 26·10³⁸ т, существенная часть приходится на межзвездный газ, пыль и т. п. Звезды словно погружены в туман из газа и мелких пылинок, имеющих размеры порядка одной десятитысячной доли миллиметра и расположенных одна от другой на расстоянии десятка метров.

Средняя плотность межзвездной материи, если бы она была распределена равномерно, составляла бы ничтожную величину²: ρ_е = 10^-23,5±1 г/см³. Это отвечает наличию от 0,2 до 20 атомов в 1 см³ пространства.

¹ Советскими учеными внесен особенно большой вклад в изучение межзвездной среды. П. П. Паренаго показал, что эта среда концентрируется в плоскости Млечного пути еще сильнее, чем звезды большинства типов. К. Ф. Огородников разработал наиболее общий метод учета поглощения света облаками межзвездной среды. В. А. Амбарцумян, Б. Р. Кукаркин, П. П. Паренаго, Б. Е. Маркарян и другие определили впервые средние физические характеристики таких облаков.

² В физической системе единиц (CGS).

Однако межзвездная материя распределена весьма неравномерно, она концентрируется к плоскости Млечного пути и собирается в облака различных размеров и плотности, которая примерно в несколько раз выше средней плотности межзвездной среды. В более плотных образованиях — газово-пылевых туманностях — концентрация межзвездной материи в 10³—10⁴ раз превышает среднюю плотность межзвездного газа. В этих облаках пыль перемешана с газовыми частицами, которых в 100 раз больше по массе, чем пыли. Принимается, что около 90% межзвездного газа — атомарный водород, остальное — натрий, калий, кальций и титан. Облака межзвездной материи перемещаются со скоростью от нескольких километров до десятков километров в секунду, а это значит, что звездный корабль будет входить в них словно самолет в облачность атмосферы. И так же как самолет поджидают в облаках опасности, например обледенение, так и галактические корабли, встречающиеся с частицами межзвездной среды, подвергаются опасности.

Прежде всего, как мы поступали и ранее, сделаем самую приближенную оценку того количества межзвездной материи, которая может взаимодействовать с ракетой за время ее полета, например, от Земли к Проксима Центавра.

Предположим, что диаметр ракеты в месте ее наибольшего поперечного сечения составляет 12 м (при длине 85 м и стартовой массе 100 т·сек²/м осредненная масса, приходящаяся на 1 м³ объема звездолета, составит около 4,5 т·сек²/м). Тогда площадь лобового сечения ракеты (или площадь, приходящаяся на каждые 100 т·сек²/м ее массы) Ф = 1,13·10⁶ см².

Подсчитаем массу межзвездной материи, заключенной в столб, у которого основание равно 1 см², а длина — расстоянию между Землей и Проксима Центавра. Поскольку расстояние между ними L =4·10¹⁸ см, а средняя плотность межзвездной среды ρ_е — 10^-23-5 г/см³, в первом приближении можем написать:

m = ρ_еL = 4·10^-5,5 г/см².(3.9)

Тогда масса столба межзвездного газа, который пройдет через поперечное сечение ракеты за весь путь в один конец, составит всего:

m' = mФ = 4·10^-6·1,13·10⁶ = 14,3 г. (3.10)

Даже при диаметре ракеты около 0,8 км, или когда 1 км² площади поперечного сечения приходится на каждые 100 т·сек²/м ее массы, через поперечное сечение ракеты прошло бы лишь немногим менее 13 кг·сек²/м межзвездной материи.

Как видно, масса межзвездной среды, попадающая в аппарат, несоизмерима даже с наименьшей массой покоя (20 т·сек²/м), которая, как было показано выше, минимально необходима для обеспечения энергетических потребностей звездолета (на каждые 100 т·сек²/м его массы) при полете к ближайшей звездной системе.

Оценим несколько более точно влияние межзвездной материи на движение ракеты, летящей с околосветовыми скоростями. При условиях, приведенных выше, в случае, когда скорость движения межзвездного газа, имеющего собственную плотность по отношению к ракете ρ_е, равна v_г, для экипажа ракеты плотность этого газа будет большей, чем ρ_е. Это закономерно¹, так как, с одной стороны, масса, содержащаяся в единице объема преодолеваемого звездолетом пространства, для экипажа представляется увеличенной в отношении 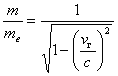и, с другой стороны, вследствие сокращения длины в направлении движения в соотношении 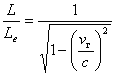. В результате плотность окружающих масс для экипажа при движении ракеты будет равна:

(3.11)

(3.12)

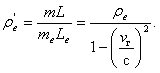
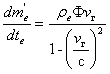
¹ Собственная скорость полета для экипажа ракеты v_е с учетом релятивистского сокращения расстояния может быть больше единицы, так как за собственную скорость принимается скорость, вычисленная по времени, прошедшему на ракете, и пройденному ракетой расстоянию, замеренному с Земли. Ниже мы остановимся на возможных значениях v_е и других приведенных здесь соотношениях несколько подробнее.

Таким образом, тормозящий импульс, приходящийся на поперечное вечение ракеты Ф, равен:

(3.13)

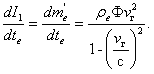
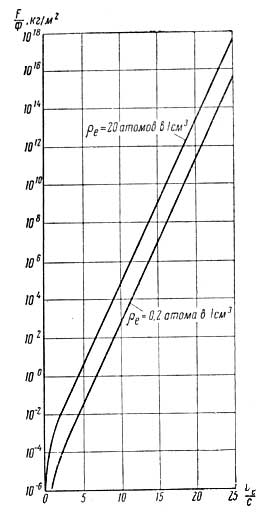Рис. 21. Тормозящее давление масс межзвездной материи в зависимости от при двух значениях плотности межзвездной среды

Результаты вычислений по уравнению (3.13) после введения в него собственной скорости полета ракеты v_e представлены для ряда значений — на рис. 21.

Если тяга ракеты создается за счет масс, принимаемых в нее из межзвездной среды, то полезная тяга составит:

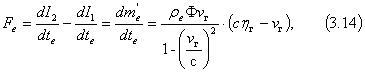
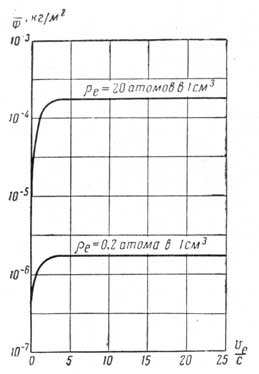Рис. 22. Полезная тяга, создаваемая за счет принимаемой в ракету межзвездной среды в зависимости от при двух значениях плотности

Как видно из графика, абсолютные значения тяги, вычисленные при средней плотности межзвездной среды, незначительны и не превышают 10^-4 кг на 1 м² поверхности поперечного сечения ракеты. Это позволяет считать, что получаемая тяга ни в коей мере не может обеспечить энергетических потребностей звездолета. Кроме того, из рис. 22 видно, что, когда скорость ракеты с точки зрения внешнего наблюдателя во много раз превышает скорость света ≫ 1 (вследствие фактического сокращения расстояния для тела, движущегося с околосветовой скоростью), тяга остается постоянной. Это происходит потому, что, хотя с ростом массы, пропускаемые через ракету, растут, разность скоростей между массами, набегающими со скоростью немного меньшей, чем скорость света, и выбрасываемыми со скоростью света, соответственно уменьшается. Напротив, как видно из рис. 21, когда ≫ 1, торможение ракеты в межзвездной среде должно становиться значительным.

В этом случае единственный способ компенсации сопротивления состоит в том, чтобы, принимая эту среду в ракету, затем непрерывно ее выбрасывать со скоростью света при полном превращении энергии набегающей массы в излучение.

Специальные вычисления, выполненные Зенгером, показывают теоретическую возможность компенсации сопротивления межзвездной среды путем использования эффекта «прямоточного двигателя». При этом основное движение ракеты будет происходить словно в пространстве, свободном от препятствующего ей газа, но разгон или торможение могут все же осуществляться лишь в результате работы электромагнитного (квантового) двигателя, использующего собственные массы, хранившиеся до этого в ракете.

Так обстоит дело с точки зрения использования межзвездного газа. Что же касается опасности контакта с ним, соударений, то она бесспорно существует. В самом деле, скорость движения уже первых галактических кораблей должна быть порядка световой, а это значит, что скорость встречи внешних стенок ракеты с частицами пыли и межпланетного газа будет близка к скоростям проникновения бомбардирующих частиц в ядра атомов конструкционных материалов ракеты.

Таким образом, помимо эрозии и взрывного взаимодействия оболочки ракеты с мельчайшими пылинками, энергия которых будет стремительно расти со скоростью полета, а также неизбежного взаимодействия с атомами газа (становящегося особенно угрожающим при их тангенциальном попадании на стенки), появляется опасность изменения свойств материала оболочки в связи с бомбардировкой ядер его атомов. Все эти воздействия могут оказаться весьма разрушительными и привести к размыванию оболочки аппарата¹ и возникновению ливней частиц, губительных для экипажа и аппаратуры. Столь же разрушительным будет воздействие космических частиц — лучей из мировых глубин.

¹ Взаимодействия такого рода были бы особенно опасны, например, для сравнительно тонкостенных оранжерей звездолета, которые, вероятно, придется использовать для обеспечения экипажа продовольствием.

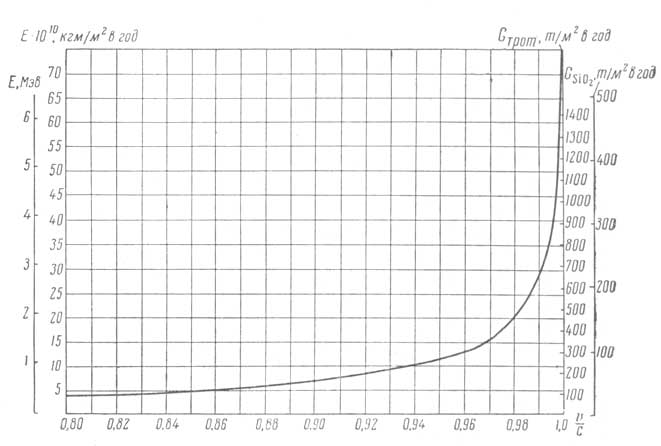Рис. 23. Энергия частиц, соударяющихся с ракетой, и необходимые массы защитной «брони» ракеты в зависимости от скорости ее полета

В этом нетрудно убедиться, познакомившись с графиком на рис. 23. По горизонтальной оси графика отложена скорость полета, отнесенная к скорости света. На первой вертикальной шкале слева энергия одного протона, встречающегося с оболочкой ракеты, на второй шкале — энергия протонов межзвездного газа, приходящаяся за год полета на 1 м² поперечного сечения ракеты (при плотности межзвездного газа ρ = 10^-24 г/см³).

На первой вертикальной шкале справа показано весовое количество тринитротолуола, которое должно быть «взорвано» на 1 м² поперечного сечения лобовой брони ракеты, чтобы выделилось столько же энергии, сколько выделяется на этой же площади при соударении с атомами межзвездного водорода. На второй шкале справа показаны примерные количества карбида кремния, которые могут испариться с м² лобовой брони ракеты в результате столкновений с частицами межзвездного газа (при условии, что оболочке передается вся энергия встречного газа).

Таким образом, график позволяет судить о массе тугоплавкого карбида, например, бериллия или других металлов, которую нужно использовать для защиты звездного корабля, если его оболочка сублимируется — возгоняется при столкновении с атомами межзвездного газа.

Возможности защиты галактического корабля от сокрушительного взаимодействия с межзвездным газом представляются по-разному в зависимости от скорости его движения: защита при скорости примерно на порядок (в десять раз) меньшей, чем скорость света, при скорости того же порядка, что и световая, но существенно меньшей, и, наконец, при скорости, вплотную приближающейся к скорости света.

Проф. Чудаков писал о том, что защита от радиации при скорости корабля 30 тыс. км/сек легко осуществима. Каждый из встречных протонов будет в таком случае обрушиваться на ракету с энергией около 2,5 тыс. эв. Протоны и электроны с такой энергией не создают сильного проникающего излучения, Кроме того, протоны, контактируясь с броней ракеты, не вызывают и электромагнитного излучения. При увеличении скорости до 100 тыс. км/сек (напомним, что эта скорость близка к наибольшей для «минимального» звездолета) вес необходимой защиты возрастет, но все же будет приемлемым. При взаимодействии межзвездного газа с ракетой при скоростях, близких (но не предельно) к световой, например при скорости 290 тыс. км/сек, масса частиц, соударяющихся с броней ракеты в единицу времени, еще относительно мала.

С того момента, когда скорость достигнет такой величины, начиная с которой на поверхности брони будут происходить ядерные процессы (примерно с 1000 км/сек), приблизительно тысячная часть соударяющейся массы газа будет переходить в излучение, а остальная энергия пойдет на разогрев и разрушение брони.

Чтобы представить себе объем «брони», который испарится и разрушится под воздействием частиц, удобно сравнить последствия космического взаимодействия с воздействием на броню определенных количеств известного взрывчатого вещества — тротила.

Пусть на 1 м² в секунду падает масса m со скоростью u. Тогда при u, близкой к скорости света с, энергия, идущая на разрушение, будет порядка mс². Величина mс² = 9·10²⁰ эрг/г. При взрыве 1 г тротила выделяется 1 кал = 4·10¹⁰ эрг — примерно в 22 млрд. раз меньше. Таким образом, 1 г массы, соударившейся с кораблем, вызовет при взаимодействии примерно такой же эффект, что и 22 тыс. т тротила.

Чтобы 1 см² поверхности «брони» встретил 1 г вещества при его плотности в пространстве 10^-24 г/см³, ракета должна пройти путь в 10²⁴ см. Поскольку расстояние до Проксима Центавра примерно в 300 тыс. раз меньше (~3·10¹⁸ см), 1 см2 поверхности ракеты встретит на этом пути всего лишь три миллионных грамма межзвездного вещества, что эквивалентно воздействию 60 кг тротила за 10 лет полета. Полет будет продолжаться около 10 лет (3·10¹⁸ сек), следовательно, каждую секунду на поверхность ракеты как бы будет воздействовать 2·10^-4 г тротила, т. е. за 1,5 часа на 1 см² взорвется всего 1 г тротила.

Конечно, приведенное рассуждение носит весьма приближенный характер. Однако можно полагать, что для защиты от воздействия межзвездного газа, помимо специальных щитов — экранов, которые предлагались инженером Ф. Ясинским¹, можно будет с успехом использовать многослойные экраны, поглощающие энергию взрыва, а также γ-лучи, образующиеся при ядерных взаимодействиях, и даже античастицы. Такие экраны могут заменяться по мере их израсходования.

¹Предлагался подвижный щит — «космический зонт», который можно устанавливать в некотором отдалении от космического корабля и даже смещать в ту сторону, с которой метеорные потоки наиболее интенсивны. Толщина щита должна быть такой, чтобы опасный метеорит пробил его. Тогда за щитом образуется газовый сгусток, который до подхода к обшивке корабля успевает остыть и частично рассеяться, превратившись в неопасное для корабля газовое облако. Высокие скорости полета, больше чем скорость хаотического движения метеоров, обеспечат создание за щитом тени, в которой космический корабль будет защищен от прямого попадания метеоритов, как человек, прячущийся от дождя под зонтом.

Приведем еще один пример, свидетельствующий о принципиальной возможности защиты ракеты от размывания межзвездной средой при скоростях порядка скорости света.

Абсолютно ясно, набегают ли частицы на звездный корабль или корабль «налетает» на неподвижные частицы, — результат один и тот же.

Положим, что на 1 см² поверхности ракеты, взаимодействующей с 1 г межзвездного вещества, приходится в 10 тыс. раз большая масса корпуса ракеты, т. е. 10 кг (такое соотношение, по-видимому, может считаться заниженным). Это означает, что, использовав всего 1/10 000 часть массы корабля, можно уничтожить космические частицы, препятствующие его движению, исключить их непосредственное взаимодействие с кораблем. Установка маломощного сравнительно с основным двигателем излучателя — квантового прожектора, бросающего перед собой электромагнитный луч, — еще один вариант активной защиты, позволяющей расчистить дорогу в межзвездном пространстве для галактического корабля.

Возможны и другие приемы. Например, целесообразно сооружение ракет с двойной оболочкой. Такая оболочка может иметь промежуточный самозатягивающийся слой, например из специальной пластмассы, в какой-то степени подобный защитному слою (протектору) из сырого каучука, который наносится на поверхности баков многих современных самолетов. При попадании на него из пробоины бензина протектор, частично растворяясь, закупоривает пробоину. Быть может, удастся создать и электромагнитную защиту. Эта защита представляется как специально возбуждаемое при прохождении опасных зон магнитное поле. Такая невидимая броня отклонит в сторону встречные заряженные частицы. Частицы же, не несущие заряда, могут быть предварительно ионизированы частью излучения, направленного вперед, и затем также отклонены с пути корабля.

Несомненно, на пути корабля может встретиться метеорит, обладающий такой энергией, что броня будет им пробита. В этом случае, может быть, удастся своевременно отклонить корабль от курса, избежав опасной встречи, и затем вновь возвратить его на курс. Авторы научно-фантастических рассказов часто описывают именно такой способ сохранения корабля невредимым. Отметим, что технически эта задача весьма сложна и, пожалуй, современными средствами радиолокации еще не может быть решена. Почему же ее решение столь сложно? Предположим, что к кораблю приближается метеорит и его скорость относительно корабля составляет 60 км/сек. Метеорит имеет массу 0,5 кг, еге эффективная отражающая поверхность около 0,01 м². Весьма совершенная радиолокационная станция мощностью 100 квт, с площадью зеркала антенны 1 м² и длиной волны 4 мм, обнаружит метеорит на расстоянии всего около 40 км. Это означает, что на определение курса метеорита, вычисление и осуществление маневра корабля останется лишь менее секунды! Практически «мгновенное» отклонение корабля осуществить невозможно.

Метеорит в 1000 раз большей массы в 500 кг может быть обнаружен той же станцией всего за 500 км, т. е. на маневр останется менее 10 сек., чего, по-видимому, также совершенно недостаточно.

С возрастанием скорости корабля все труднее осуществить его даже самое незначительное отклонение от курса, так что при скорости порядка скорости света, по-видимому, придется искать пути уничтожения метеоритов, а частицы межзвездного газа принимать на защитные экраны и броню галактического корабля.

Естественно, что в ходе преодоления трудностей, связанных с размыванием материала ракеты и изменением его свойств, могут быть и будут найдены такие принципиально новые материалы, конструктивные и технологические решения, которые сейчас предсказать невозможно. Все это несомненно поможет преодолеть околосветовой барьер.

Наконец, остановимся на возможностях защиты корпуса ракеты при скорости, вплотную приближающейся к скорости света. Эта задача представляет сейчас лишь академический интерес, однако парадоксальный на первый взгляд вывод, к которому приводит ее рассмотрение, очень любопытен.

Можно ожидать, что в этом случае при взаимодействии корпуса ракеты с частицами межзвездного газа (масса которых согласно теории относительности резко возросла) возникнет излучение, исходящее из брони ракеты и направленное вперед. Этот луч будет воздействовать на новые частицы, летящие навстречу ракете, и они в свою очередь превратятся в излучение. Весьма быстро установится такой режим обтекания ракеты потоком частиц, когда на некотором расстоянии от нее практически вся масса встречного газа будет переходить в излучение.

Для поддержания подобного режима самоэкранировки достаточно, чтобы на поверхность ракеты падала ничтожнейшая (всего 1/100 000) часть встречных частиц, так как уже при скорости 1000 км/сек начинаются ядерные процессы, поддерживающие такой режим.

Поверхность, где совершается «переработка» космических частиц в излучение, будет находиться на большом расстоянии от звездного корабля, и поэтому общее количество излучения, дошедшее до него, по-видимому, будет в сотни тысяч раз меньше, чем при непосредственном воздействии частиц на «броню» ракеты. Если перед кораблем расположить сравнительно тонкий свинцовый зонт, звездолет подвергнется умеренному воздействию межзвездной материи.

Рассказывая о распределении межзвездного газа и пыли в пространстве, мы отмечали, что, наряду с областями, в которых плавают облака с повышенной концентрацией материи, есть и такие, где концентрация межзвездного вещества мала, — своеобразные прозрачные дороги. Разумеется, что по ним и должны будут направляться звездные корабли.

Нами были описаны решения проблем, которые на первый взгляд могут показаться неразрешимыми. Приемы, которые сегодня удается наметить, конечно не единственные, и это само по себе еще раз показывает, что и другие препятствия, стоящие на дороге к звездам, будут успешно преодолены.

В частности, целый комплекс задач возникнет в связи с необходимостью создать в условиях длительной невесомости привычные условия для жизни и работы астронавтов, необходимостью обеспечить защиту кабины и самих астронавтов от космических частиц, от излучений энергетического источника звездолета и других внешних воздействий. На некоторых особенностях этих проблем, в известной степени специфических для звездолетов, мы вкратце и остановимся.

Человек в звездолете

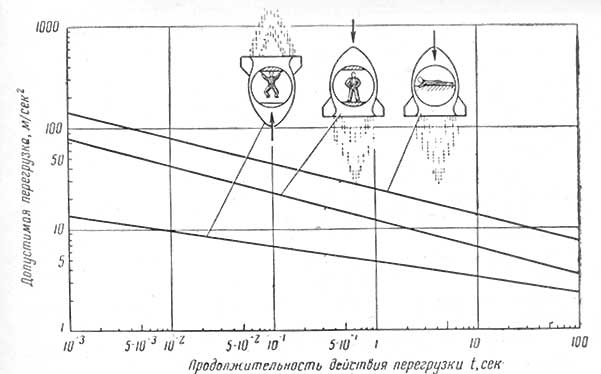Рис. 24. Допустимые перегрузки и их возможная продолжительность в зависимости от положения человека в ракете. Направление действия перегрузки показано стрелками

Взлет космического корабля с Земли, а также его торможение с использованием двигателей и сопротивления атмосферы при возвращении на Землю связаны со значительными ускорениями, т. е. с существенными изменениями скорости по величине и направлению. Это неизбежно сопровождается воздействием на весь летательный аппарат, его оборудование и находящихся в нем людей механических сил, которые вызывают и определяют величину перегрузки, т. е. отношение силы, с которой тело давит на опору, к весу этого тела.

Опыт, накопленный в авиационной технике, свидетельствует о том, что наибольшие нагрузки, которые может вынести человек без вреда для здоровья, зависят как от его положения в разгоняющемся аппарате, так и от продолжительности действия перегрузки. График, показывающий ориентировочные допустимые перегрузки в зависимости от положения человека, приведен на рис. 24. Из этого рисунка, в частности, видно, что организм значительно лучше переносит поперечную перегрузку, чем продольную. Если перегрузка действует вдоль тела человека, то, чтобы поднять «тяжелую» кровь на необходимую высоту, сердце совершает большую работу. Если же человек «лежит», перегрузка действует поперек тела, высота меньше и сердце успешнее справляется со своей задачей.

Задачи выбора соотношения длительности и величины перегрузок, которые не будут вредно отражаться на здоровье человека, решаются сейчас и будут решаться уже в процессе создания обитаемых спутников-станций.

Для «минимальных» звездолетов, стартующих со спутников, будут, вероятно, характерными весьма малые постоянные ускорения. Когда же наступит время создания несколько более совершенных аппаратов, они будут двигаться на значительной части пути с выключенными двигателями, а значит без ускорений и без ощущения «веса» у находящихся в них людей, и для восстановления хотя бы части веса понадобятся специальные приемы.

Только в весьма отдаленном будущем при достижении скоростей, вплотную приближающихся к скорости света, на аппаратах с практически неограниченными энергетическими возможностями, способных преодолевать расстояния в сотни световых лет с большими ускорениями и относительно ничтожным собственным временем полета, снова, как для современных ракет, стартующих с Земли, возникнет проблема разгона с максимальными перегрузками.

Итак, поскольку в обозримом будущем для экипажей звездолетов могут быть характерными именно малые перегрузки, остановимся вкратце на проблеме воздействия на человека невесомости, которую К. Э. Циолковский начал изучать еще в 1876 г.¹

На звездолет, удаляющийся от Земли, ее притяжение практически перестает действовать уже с расстояния 1 млн. км, а поскольку гравитационные поля в межзвездном пространстве ничтожны, все тела в нем окажутся в положении так называемой статической невесомости ².

¹ К. Э. Циолковскому принадлежит особое место в создании космической медицины. В 1876—1878 гг. он провел опыты, в ходе которых пытался решить некоторые медико-биологические проблемы полетов за пределы Земли.

² В случае, когда спутник движется по круговой орбите со скоростью, например, около 8 км/сек и центробежная сила полностью уравновешивает силу притяжения, потеря веса обусловливается скоростью спутника и называется поэтому динамической невесомостью.

Потеря веса не означает, однако, потери массы. Инертность тел остается, и, значит, для изменения скорости корабля всегда потребуется приложить к нему силу тяги.

Первые достоверные сведения о продолжительном воздействии невесомости на живой организм были получены при запусках спутников с животными, в частности, в ходе успешного полета Лайки на втором советском искусственном спутнике Земли. Как известно, Лайка быстро освоилась с невесомостью и чувствовала себя нормально.

Поскольку при движениях в условиях невесомости человеку требуется, например, преодолевать вес рук и ног, первоначально, как свидетельствуют специально проведенные экспериментальные исследования, происходит нарушение координации точности движений. Однако опыты показывают, что предварительная тренировка позволяет человеку быстро освоиться с новыми условиями.

Юрий Гагарин рассказал, что в ходе своего полета после наступления невесомости он не ощущал ничего неприятного. Важно было выяснить, можно ли привыкнуть к более длительному пребыванию в условиях невесомости. Герман Титов провел в таких условиях сутки и чувствовал себя отлично. Кровообращение, координация движений, сон, прием пищи были нормальными.

Можно надеяться, что люди, пройдя школу невесомости на первом этапе освоения космоса в течение многомесячных путешествий в Солнечной системе, сумеют решить эту проблему и для десятков лет полета в межзвездном пространстве. Наконец, в случае необходимости весомость может быть, как известно, получена искусственно, путем равномерного вращения кабины галактического корабля вокруг продольной оси. Кроме того, на первых порах, до выработки необходимых навыков, для облегчения движения людей в условиях невесомости можно будет использовать магнитный пол, резиновые присоски на обуви и другие подобные средства.

Все же следует иметь в виду, что первые межзвездные полеты, связанные с оторванностью не только от Земли, но и от Солнечной системы, необычайность самого путешествия, предстоящие величайшие открытия создадут своеобразное психологическое состояние экипажа.