Для того чтобы послать ракету на Луну, необходимо прежде всего сообщить ракете начальную скорость 10 380 м/сек на высоте 830 км над поверхностью Земли.
Продолжительность путешествия составит около 97 час. Однако мы считаем, что для того чтобы ракета на самом деле встретилась с Луной, она должна обладать несколько большей скоростью.
Действительно, если p — скорость, с которой ракета должна вылететь, чтобы при совершенно безошибочном управлении подняться выше нейтральной точки (граница между полями тяготения Земли и Луны), v — действительная скорость ракеты и если v ≠ p, то в нейтральной точке ракета обладает некоторой остаточной скоростью r, величина которой согласно (120) равна
|
|
r является здесь функцией v, и дифференцированием мы находим:
![]()
Это выражение обращается в бесконечность при v = p. Но продолжительность полета в очень сильной степени зависит от r и при значениях v, близких к значению p, разница скорости, не превышающая несколько миллиметров в секунду, была бы достаточна, чтобы изменить продолжительность полета на несколько часов. При этом вероятность, что ракета вообще встретит Луну, становится сомнительной. Таким образом будет лучше, если ракете для межпланетных полетов будет сообщена начальная скорость, по меньшей мере равная 10 500 м/сек.
Как было показано выше, идеальная скорость должна быть на 700 м/сек больше конечной скорости. Таким образом при старте с Земли нужна идеальная скорость 11 200 м/сек. По ту сторону нейтральной точки ракета, будучи предоставлена своей судьбе, будет падать все быстрее и, наконец, упадет на Луну с такой скоростью, что безусловно разобьется. Луна сообщает падающему на нее с большой высоты телу скорость vp = 2370 м/сек.
Если же ракета уже в нейтральной точке обладала скоростью vr, то скорость vs, с которой она ударится в Луну при падении, определится, согласно (120):
![]()
Поскольку остаточная скорость vr относительно Земли и тангенциальная скорость vt относительно Луны взаимно перпендикулярны, то можно также написать
vr² = vt² + r² (221)
и, согласно (218),
r² = v² - p²
Из формул (218) — (221) в полном согласии с формулой (120) получаем:
![]()
Это дает при v = 10 500 м/сек (прочие величины являются астрономическими константами)
vs = 3027 м/сек
т.е. около 3 км/сек.
Чтобы предохранить ракету от разрушения, необходимо перед самым падением ракеты на поверхность Луны затормозить эту скорость. Поскольку Луна лишена воздушной оболочки, это может быть достигнуто лишь посредством реактивной силы, противодействующей движению. В результате получим дальнейшее приращение требуемой идеальной скорости на 3 км/сек.
Но эти 3030 м/сек еще далеко не разрешают проблемы. Ракета должна опуститься мягко, как падают снежные хлопья. Ведь она сделана из тонкого листового металла, который вследствие соприкосновения с жидким водородом становится >до меньшей мере таким же хрупким, как листовая сталь при обычной температуре. В то же время при посадке нельзя допустить никаких трещин и разрывов оболочки ракеты. С нижней стороны ракеты можно, конечно, приделать крепкие пружинящие стойки, но все же посадка должна совершаться очень осторожно.
Нельзя представить себе, что водитель ракеты даст ей свободно падать до последнего мгновения и затормозит лишь в самом конце при максимально допустимом опорном ускорении. По всей вероятности, водитель уже гораздо раньше затормозит большую часть скорости ракеты и затем будет спускаться при почти равномерной скорости, постоянно компенсируя ускорение силы тяжести при помощи реактивной силы, и, наконец, на расстоянии метра от поверхности Луны совершенно остановится и опустится постепенно, сантиметр за сантиметром. Недостаток этого способа заключается, конечно, в том, что ракета в течение очень долгого времени должна противодействовать собственному весу, или, как мы говорили об этом в гл. IX, двигатель должен будет работать при малой скорости полета.
Ускорение силы тяжести составляет на Луне около 1,62 м/сек². Если первое торможение скорости на 3027 м/сек происходит при опорном ускорении, равном 35 м/сек², то на это торможение требуется 1,5 мин. (если направление движения не перпендикулярно к поверхности Луны, то даже несколько меньше). Но последующий осторожный спуск вполне может потребовать в 4 — 5 раз больше времени; в целом необходимо рассчитывать на работу двигателя в продолжение 9 мин. = 540 сек. При ускорении силы тяжести 1,62 м/сек² это дает дополнительную потерю скорости 873 м/сек.
Допустим, что наши путешественники по межпланетному пространству счастливо прибыли на Луну. Но они, естественно, хотят вернуться назад. Это им удастся лишь, если они смогут вновь запустить двигатель ракеты, с тем чтобы она смогла подняться с Луны и упасть на Землю. Такой подъем был бы точным обращением процесса падения ракеты на Луну, так как бросок вверх физически представляет собою противоположность свободного падения. В количественном отношении мы имеем то же, что и по формуле (131); другими словами, действительная скорость старта должна быть vs = 3027 м/сек. В этом случае можно сейчас же дать полный газ. При идеальном ускорении 35 м/сек² и при горизонтальном старте угол атаки ε определяется следующим образом:
![]()
Потерями скорости во время вертикального старта можно здесь вообще пренебречь. Ракета должна подняться лишь на такую высоту, чтобы не задевать вершин лунных гор.
Тогда получим:
vx < 3027 · sec 2.63º = 3030 м/сек
Мы рассчитываем лишь на горизонтальный старт, так как ракета может стартовать с любого места, где бы она ни находилась горизонтально. Вначале она полетит, таким образом, с круговой скоростью, описывая окружность вокруг Луны. Направление скорости, с которой она должна стартовать, чтобы вернуться на Землю, должно лежать в плоскости этой окружности. Как только движение ракеты станет параллельным желаемому направлению, реактивная сила должна увеличить круговую скорость до требуемых 3027 м/сек. Впрочем, благодаря малой величине силы тяжести на Луне ракета и при вертикальном старте потеряет лишь 160 м/сек идеальной скорости.
Смотря по тому, снабжена ли ракета несущими плоскостями или парашютом, приземление на Землю требует еще до 200 м/сек идеальной скорости.
Поскольку водитель может совершать промахи, то он должен в целях корректирования возможных ошибок взять горючего еще примерно на 1000 м1сек (мы считаем, что этого количества будет вполне достаточно). Полная идеальная скорость, должна равняться сумме перечисленных ниже отдельных скоростей (в м/сек):
| скорость подъема с Земли |
11 200 |
| торможение скорости падения на Луну |
3 027 |
| потери на торможение при посадке |
873 |
| старт с Луны |
3 030 |
| корректирование траектории |
1 000 |
|
Всего.......vx = 19130 м/сек | |
Если принять скорость истечения с = 4000 м/сек, то, согласно формуле [(6) гл. III], идеальное отношение масс для такой ракеты будет m0/m1 = 134. Такой полет могла бы совершить ракета, составленная из трех водородных ракет. Благодаря своей величине она обладала бы достаточной нагрузкой на поперечное сечение, несмотря на исключительную легкость топлива.
Посещение Луны могло бы иметь огромный научный интерес. Луна представляет собою небесное тело, состоящее в основном из тех же веществ, что и Земля, хотя Земля получила сравнительно больше тяжелых, а Луна — больше легких веществ. Таким образом поверхность Луны состоит в основном из тех же пород, что и поверхность Земли, с той лишь разницей, что лунная поверхность не была подвержена действию воздуха и воды. Сравнение обеих поверхностей даст нам возможность установить, что именно на поверхности нашей Земли вызвано действием воздуха и воды и что не зависит от влияния этих двух факторов. Далее, на Луне мы могли бы вырыть шахты и пробурить скважины в четыре раза более глубокие, чем на Земле. Малая сила тяжести и ожидаемая твердость пород воспрепятствуют сжатию скважин, наблюдаемых на Земле. Кроме того, внутри Луны царит не такая высокая температура, как внутри Земли, и потому в глубоких лунных шахтах жара меньше, чем в шахтах на Земле. Но в четыре раза более глубокая буровая скважина на Луне имеет относительную глубину не в четыре, а в 10 — 12 раз большую, чем на Земле, так как диаметр Луны в три раза меньше диаметра Земли. Такие глубокие шахты и скважины позволят сделать очень интересные геологические открытия.
Кроме перечисленных выше научно-исследовательских целей полета на Луну, можно указать также одну чисто практическую цель, которая, по всей вероятности, может стать актуальной в течение одного - двух ближайших десятилетий. Существует мнение, что лунные кратеры образовались вследствие того, что на Луну в то время, когда она находилась уже в застывшем состоянии, падали многочисленные большие метеориты. Эти метеориты состояли в основном из тяжелых металлов. Но наша Земля в основном состоит из тяжелых металлов. Данные сейсмологии показывают, что на глубине 1500 км сравнительно легкий слой, образующий поверхность Земли, внезапно кончается и с этой глубины начинается слой, имеющий удельный вес железа. На Землю также падали многочисленные метеориты, когда она находилась в стадии своего образования. Но Земля находилась тогда еще в огненно-жидком состоянии и тяжелые вещества опускались книзу. На Луне же, напротив, эти тяжелые вещества оставались на ее поверхности, и потому их сравнительно легко можно было бы разбить на отдельные куски и отправить на Землю. Для этого требуется лишь преодолеть небольшую силу притяжения Луны.
2. Астероиды
Принятые обозначения
|
|
Между орбитой четвертой планеты в солнечной системе (Марс) и пятой (Юпитер) расположены орбиты многочисленных, сравнительно небольших небесных тел — так называемых планетоидов, астероидов или малых планет. До сих пор их было открыто около тысячи, но, вероятно, их гораздо больше. Очевидно, не открытые еще астероиды настолько малы, что их не удается наблюдать ни визуально, ни при помощи фотографии.
Орбиты астероидов занимают кольцеобразное пространство, более широкое, чем диаметр земной орбиты. В среднем астероиды отстоят от Солнца на расстоянии, равном трем радиусам орбиты Земли, но некоторые из них почти достигают орбиты Юпитера (пять радиусов орбиты Земли), а другие подходят почти вплотную к орбите Марса (полтора радиуса орбиты Земли). Один из астероидов (Эрос) большую часть своего обращения совершает внутри орбиты Марса, так что орбиты этих двух небесных тел представляют собою как бы два кольца цепи, вставленных одно в другое.
Наибольший астероид (Церера) имеет в диаметре почти 900 км; самые маленькие астероиды едва видны в лучшие телескопы; диаметры их, несомненно, не превышают нескольких километров. Альбедо (т.е. отношение количества света, которое отражается небесным телом, к количеству света, которое им поглощается) для различных астероидов может быть весьма различным. Альбедо Цереры составляет 10%, таким образом Церера по своему цвету является почти черной. Напротив, альбедо Весты составляет более 60%, таким образом Веста должна обладать белой или блестящей поверхностью. Это приводит нас к заключению, что различные астероиды состоят из различных веществ.
Массы и силы притяжения астероидов нам почти неизвестны, но вследствие небольших размеров астероидов они во всяком случае очень малы. Так, например, ускорение силы тяжести на Церере немногим превышает 50 см/сек², а параболическая скорость — 800 м/сек. Для самых маленьких астероидов действием силы тяжести можно пренебречь. Мы не знаем, имеется ли на некоторых астероидах атмосфера. Во всяком случае большинство из них вследствие малой силы притяжения не в состоянии удержать ни воды, ни воздуха. Некоторые астероиды обнаруживают периодические колебания блеска (яркости). Это можно объяснить тем, что астероиды представляют собою тела не шарообразной, а неправильной формы, которые поворачивают к Солнцу то более широкие, то более узкие поверхности.
Полет на один из астероидов представляет собою новую задачу по сравнению с рассмотренным нами ранее полетом на Луну, поскольку в этом случае ракета для межпланетных путешествий должна быть перемещена на значительное расстояние относительно Солнца.
Если ракета покидает Землю с гиперболической скоростью v1 и если параболическая скорость в той точке, где прекращается работа двигателя, равна vp, то, согласно (120), вне сферы действия земного притяжения ракета обладает относительно Земли остаточной скоростью vr = √(v1² - vp²). Теоретически область земного притяжения нигде не кончается, но практически радиус ее можно считать равным 1 млн. км. Это значит, что по ту сторону от указанной границы притяжение Земли становится таким незначительным по сравнению с притяжением других небесных тел, в частности, Солнца, что в первом приближении им вполне можно пренебречь.
При этих полетах ракета опишет траекторию, точное вычисление которой чрезвычайно сложно.
Пирке и Гоману удалось показать, что задача относительно траектории ракеты для межпланетных сообщений может быть решена, по крайней мере приближенно, при помощи сравнительно простых вычислительных методов.
Приближенно можно считать, что в поле силы тяжести Земли ракета для межпланетных сообщений летит по гиперболе. Вне поля силы тяжести Земли она продолжает лететь со скоростью w1 которая может быть разложена как вектор, на тангенциальную скорость Земли относительно Солнца wt и остаточную скорость самой ракеты vr. В результате ракета для межпланетных путешествий опишет линию, представляющую собою некоторое коническое сечение, в одном из фокусов которого находится Солнце. В этом случае приложимы расчеты, приведенные в гл. VII, причем за α, следует взять угол между w и wt.
Если введем обозначения: r1 — радиус орбиты Земли, r2 — расстояние астероида от Солнца, g1 — сила притяжения Солнца на расстоянии Земли, g2 — притяжение Солнца на расстоянии астероида и w — скорость ракеты на расстоянии астероида, то, согласно (59), будем иметь:
![]()
Если α обозначает угол наклона к горизонтали (относительно Солнца), то, согласно (55а),
r1 w1 cos α1 = r2 w2 cos α2 (224)
Из (223) и (224) следует:
![]()
При помощи этой формулы можно вычислить угол, который траектория образует с горизонталью на определенной высоте r1 или r2, а также решить обратную задачу, т. е. для заданного угла α2 найти высоту r2, на которой траектория образует с горизонталью данный угол.
Рассматривая орбиты Земли и той планеты, на которую должен совершиться полет, как окружности, мы получим, что расход топлива будет наименьшим, если ракета будет лететь по полуэллипсу, который в перигелии (т. е. вблизи Солнца) касается орбиты Земли, а в афелии — орбиты планеты (при этом, конечно, предполагается, что планета в заранее вычисленный момент пройдет через определенную точку на своей траектории; таким образом при этом методе момент вылета нельзя устанавливать по желанию).
В этом случае
![]()
Ракета при этом сначала летит перед Землей, и ее остаточная скорость vr1 складывается с тангенциальной скоростью Земли wt1.
Тогда
w1 = wt1 + vr1 (227)
В то же время, когда ракета летит перед Землей, она одновременно удаляется от Солнца благодаря большой центробежной силе. При этом ее скорость замедляется. В афелии ее скорость меньше, чем скорость планеты, в противном случае она должна была бы продолжать лететь по окружности, а не по эллипсу. Если wt2 — тангенциальная скорость планеты, то остаточная скорость ракеты относительно планеты
vr2 = wt2 - w2 (228)
Из (225) и (226) следует:
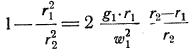
Как известно, w²t1 = g1r1; поэтому
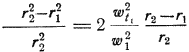
или
![]()
Из (227) и (229) следует тогда:
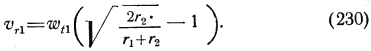
Из (225), (226) и (228) мы находим аналогичным способом [так же, как из (230) при соответственной замене букв и изменении знаков]:
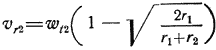
или, так как
![]()
то
![]()
Если поставим себе задачей достичь небесного тела, обращающегося с круговой скоростью на расстоянии трех радиусов орбиты Земли, то, согласно (230) (принимая wt1 = 29,7 км/сек), получим vr1 = 6,55 км/сек. При сложении импульсов [см. (120)] v1 = 13,1 км/сек. Идеальная скорость составит 14 км/сек.
Увеличением остаточной скорости vr2 под влиянием притяжения астероида обычно можно пренебречь вследствие малой массы астероида и сравнительно большой величины остаточной скорости. Поскольку астероиды, по всей вероятности, лишены атмосферы, эта скорость должна быть заторможена действием самой ракеты, причем мы должны принять vx = vr2. При старте в обратный путь такой же импульс должен быть дан в обратном направлении. Для осуществления посадки и корректирования ошибок полета необходимо взять с собой топлива еще на 1000 м/сек. Встреча с астероидом значительно легче, чем с Луной, так как в этом случае ракета летит в том же направлении, что и небесное тело, а не перпендикулярно его траектории. Таким образом полная идеальная скорость ракеты должна быть около 25 км/сек.
Такую мощность может развить водородная четырехступенчатая ракета, но при современном состоянии техники возникают сомнения в возможности конструирования таких ракет*. К счастью, в этом нет особой необходимости. Мы можем перед полетом при помощи маленьких ракет переправить топливо на топливную станцию, которая с круговой скоростью движется по окружности вокруг Земли. Окружность эта должна быть расположена таким образом, чтобы при последующем вылете ракеты с топливной станции направление ее полета лежало в плоскости этой окружности.
Если такая топливная станция находится на той высоте, на которой ракета при подъеме по кривой синэргии достигает круговой скорости, т.е. если она лежит над границей земной атмосферы, то это причаливание ракеты к топливной станции и заполнение ее топливом теоретически не означает потери скорости, так как при вылете новый импульс есть синэргическое продолжение импульса, который был сообщен топливу уже ранее. Круговая скорость является в известном смысле пунктом отдыха, так как по ее достижении старт может быть прерван на произвольно долгое время без нарушения принципа сложения импульсов и принципа полета с наибольшим возможным ускорением.
При этом (по крайней мере в отношении полета на астероид) нет никакой необходимости, чтобы топливная станция находилась над экватором.
Конечно, вылет ракеты для межпланетных путешествий с топливной станции только в том случае является синзргическим продолжением ее полета на астероид, если топливная станция находится именно там, где кривая синэргии идет горизонтально. Если, как предлагает Ноордунг, поместить топливную станцию так высоко над Землей, что она будет совершать одно обращение вокруг Земли за 24 часа, и если она всегда будет находиться над меридианом одного и того же места, то это, конечно, будет весьма привлекательно с точки зрения ее связи с Землей, но, согласно сказанному в гл. IX, это вовсе не значит, что она занимает наиболее выгодное положение в качестве топливной станции. Точно так же, если, как предлагает Пирке, заставить наблюдательную станцию обращаться на высоте радиуса Земли над земной поверхностью, то это будет очень удобно для наблюдения, но если мы захотим воспользоваться этой наблюдательной станцией также в качестве топливной станции, то потеряем около 100 м/сек идеальной скорости.
Таким образом с синэргической точки зрения лучше организовать топливные станции отдельно от наблюдательных и зеркальных станций. Но это не является безусловно необходимым, так как при этом мы получим потерю скорости самое большее лишь на 100 м/сек.
При полете на астероид, который движется по эллиптической орбите, остаточная скорость определится как векторная разность между скоростьк> ракеты и скоростью планеты.
Приведем формулы для случаев, когда ракета должна достичь астероида в перигелии или в афелии. Обозначим через r1 — радиус орбиты Земли, r2 — расстояние астероида в перигелии, r3 — его расстояние в афелии, V2 — скорость астероида в перигелии, V3 — его скорость в афелии, w2 — скорость ракеты относительно Солнца при полуэллиптическом полете в перигелии, w3 — скорость ракеты относительно Солнца в афелии астероида, vr2 и vr3 — соответствующие остаточные скорости относительно астероида. Подставляя соответствующим образом эти величины в формулу (229), найдем:
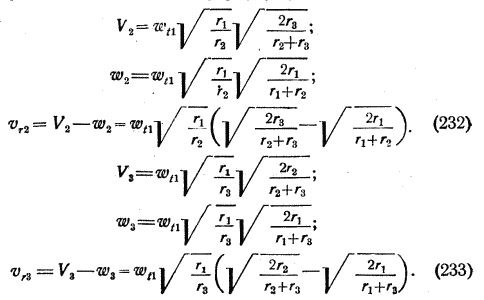
Остаточную скорость относительно Земли vr1 найдем из (230), подставляя вместо r2 расстояние до астероида в перигелии или в афелии.
К небесному телу, лишенному атмосферы, и обращающемуся по сильно эллиптической орбите, гораздо легче приблизиться в афелии, чем в перигелии, так как при этом vr2 будет меньше, a v1 увеличится лишь незначительно.
Но такой полет по полуэллипсу обладает одним существенным недостатком — он длится очень долго. Если обозначить через r1 радиус земной орбиты, а r2 расстояние пункта назначения от Солнца, то, имея дело с полуэллипсом, можем написать по третьему закону Кеплера:
![]()
Например, в первом из названных случаев путешествие только в одну сторону займет 1 год 4 мес. и 28 дней. Затем ракета должна ждать на астероиде 2 мес, пока не наступит удобный момент для возвращения назад, которое, конечно, продлится ровно столько же, сколько и полет на астероид. Таким образом все путешествие займет 3 года.
Здесь можно помочь лишь одним — лететь быстрее. При этом и траектория полета значительно сокращается. Кроме того, улучшается «прицельность» полета.
Если ракета должна достичь орбиты планеты в афелии, то вероятность встречи с планетой большая. Напротив, на примере полета на Луну мы уже видели, как легко пропустить небесное тело, если траектория ракеты образует большой угол с направлением движения этого небесного тела.
Как уже было указано, некоторые астероиды находятся к нам значительно ближе. Например, Эрос подходит к Земле ближе, чем все другие небесные тела, не считая, конечно, Луны. Полет на Эрос при минимальном расходе горючего занял бы от 1/2 до 3/4 года (все путешествие потребовало бы несколько больше 3 лет). Для полета потребовалось бы достижение идеальной скорости 17 км/сек, включая потери на торможение и корректирование ошибок траектории. Таким образом с точки зрения расхода топлива из всех тел солнечной системы, включая и Луну, наиболее легко достижимым является именно Эрос. При этом расход горючего, соответствующий vx = 20 км/сек, мог бы сократить продолжительность полета до 2 лет.
Цель полета. Посещение этих небесных тел, которые вследствие своей малости остаются почти неизученными астрофизиками, само по себе было бы весьма интересным и поучительным. Кроме того, для развития астрономии было бы весьма важно, если бы на маленьких астероидах (например, на Эросе) удалось установить телескопы.
Что касается возможных результатов таких экспедиций для геологии, то в этом случае с еще большим правом можно повторить все сказанное относительно Луны.
На астероидах диаметром менее 300 км можно вырыть шахту, доходящую до центра планеты; это дало бы возможность всесторонне исследовать внутреннюю структуру небесного тела, которое, хотя и гораздо меньше Земли, но все же в некоторых отношениях подобно ей (шарообразная форма, состав и т. д.).
Особенно большое научное значение имело бы исследование астероидов потому, что мы имеем здесь все переходы от планет (Марс — Церера — Паллада — Психея и т. д.) к кометам (Эрос — комета Энке) и к скоплению метеоритов.
3. Марс
Марс обращается вокруг Солнца по эллипсу. Большая полуось его орбиты равна
1,5236914 радиуса земной орбиты; эксцентриситет орбиты Марса равен 0,0933574.
Послав ракету на Марс по описанной выше траектории, представляющей собой
половину эллипса, получим весьма различные остаточные скорости в зависимости от
того, требуется ли достичь Марс в его перигелии или в его афелии. В перигелии
остаточная скорость относительно Земли при вылете будет равна vr1 = 2,16 км/сек [см. формулу (234)], а
остаточная скорость относительно Марса при прибытии составит vr2 = 3,27 км/сек.
В афелии мы получим соответственно: vr1 = 3,50 км/сек, vr2 = 2,00 км/сек. Однако, поскольку и Земля и
Марс обладают значительной массой и потому большой параболической скоростью, то
эти остаточные скорости на идеальную скорость влияют мало. При этом нельзя
пренебречь тем, что оба эти небесных тела обладают атмосферами, которые можно
использовать для торможения, так что величина остаточной скорости при прибытии
вообще безразлична. Но все же необходимо рассчитывать на то, что последние 400 —
700 м/сек скорости придется затормозить посредством реактивной силы, так как
атмосфера Марса во всяком случае очень разрежена. Если пожелаем посетить Марс
так, чтобы к моменту прибытия ракеты он находился в перигелии, то необходимая
конечная скорость при вылете должна быть равна v1 = 11,3 км/сек. При посадке на Марс
потребуется для торможения самое большее 700 м/сек. Полная идеальная скорость
полета на Марс, включая потери при старте около 700 м/сек, а также 600 м/сек для
целей корректирования, составит 13 300 м/сек. Параболическая скорость для Марса
равна 4,96 км/сек, ускорение силы тяжести лишь 3,50 м/секα, а атмосфера, вообще
говоря, более разрежена, чем на Земле, хотя, вероятно, и достигает несколько
большей высоты. Поэтому при вылете с Марса мы сравнительно мало потеряем в
идеальной скорости (возможно, 300 м/сек). На обратном пути v2 = 5,94 км/сек, и если мы снова положим 500
м/сек для целей корректирования полета и предусмотрим торможение в земной
атмосфере, то для обратного пути потребуется самое большее vx = 6,7 км/сек. Весь полет потребовал бы около
vx = 20 км/сек, т.е. несколько
больше, чем полет на Луну.
Когда Марс находится в афелии, то, как легко убедиться из вычислений, мы
получим vx = 19,8 км/сек.
Полет происходил бы с наименьшим расходом горючего, если бы мы прилетели на
Марс в тот период, когда планета находится в перигелии, и могли бы оставаться на
Марсе столь долго, чтобы вылететь при его положении в афелии. Теоретически это с
некоторым приближением возможно, так как при таком полете придется ждать момента
возвращения в течение половины марсианского года. (При этом мы пока не касаемся
вопроса о том, можно ли в действительности сохранить топливо в жидком виде в
течение целого года.)
Продолжительность полета на Марс вообще легко сократить, повысив скорость,
так как при больших параболических скоростях Земли и Марса небольшое повышение
начальной скорости уже сильно влияет на остаточную скорость, а так как, кроме
того, скорость тормозится в атмосфере, то нет необходимости в расходовании
топлива на торможение. Например, при
= 25 км/сек все путешествие туда и обратно можно совершить за 4 — 6 мес. и
при этом не придется лететь вокруг Солнца. В особенности сильно может быть
сокращена продолжительность первой половины путешествия, т.е. полета с Земли на
Марс, причем это не потребует значительного повышения скорости.
Путешествие на Марс значительно облегчается, так как там имеется вода в
достаточном количестве и небо большей частью ясное. На Марсе, несомненно, можно
было бы установить машины для получения жидкого топлива, работающие с
использованием солнечной энергии и разлагающие воду на водород и кислород.
Благодаря этому, во-первых, на Марсе можно было бы оставаться как угодно долго,
несмотря на испарение топлива, а, во-вторых, не нужно было бы брать запас
топлива на обратную дорогу. Это позволило бы сэкономить по меньшей мере б
км/сек. Если бы на Марсе была установлена такая топливная станция, то с точки
зрения топлива путешествие на Марс было бы легче, чем на какое-либо другое тело
солнечной системы.
Цель полета на Марс. Что касается целей путешествия на Марс, то
читатель, ожидающий слишком многого, может разочароваться. Единственное, что
можно обещать наверняка, — это разрешение большинства загадок, которые
представляет нам наша соседняя планета. Различные гипотезы, относящиеся к Марсу,
часто защищаются с огромной убедительностью, и неспециалист слишком легко может
принять эти гипотезы за научно доказанные факты*.
4. Венера
Венера является наиболее трудно достижимым, но в то же время наиболее
интересным небесным телом для путешественника по межпланетному пространству.
По величине и химическому составу Венера почти совершенно сходна с Землей
(диаметр ее равен примерно 12 300кл«). Атмосфера ее, повидимому, на 10 — 20 км
выше, чем земная атмосфера. Поэтому давление воздуха на видимой поверхности
Венеры в 2 — 3 раза больше нормального давления воздуха на Земле.
Альбедо Венеры составляет 0,71 — 0,76% таким образом области Венеры,
освещенные Солнцем, поглощают лишь 24—29% падающего на них количества света.
Остальные 71 — 76% они отражают назад. Эта цифра очень велика и соответствует
отражательной способности плотного снежного или облачного покрова.
В телескоп Венера при хороших условиях видимости кажется небольшим
полумесяцем. Когда Венера ближе всего к нам, она находится между Землей и
Солнцем и мы ее вообще не видим (так называемое нижнее соединение). Когда Венера
занимает такое положение, что Солнце находится между ней и Землей (так
называемое верхнее соединение), то мы также не можем ее наблюдать. Когда Венера
близка к верхнему соединению, она кажется нам маленьким диском; к сожалению, в
это время она находится довольно далеко от Земли.
В телескоп Венера представляет наблюдателю ровную яркую белую поверхность, на
которой нельзя различить ни малейших деталей. Темные пятна, которые иногда
представляются наблюдателю после долгого наблюдения и которые плохими аппаратами
можно даже фотографировать, объясняются просто эффектом диафрагмирования. Они
бывают видны на каждой ярко освещенной сфере ровного белого цвета и исчезают тем
бесследнее, чем лучше инструменты, при помощи которых производится наблюдение
Венеры. Таким образом Венера является весьма неблагодарным объектом для
наблюдателя.
Относительно температуры Венеры трудно сказать что-либо определенное. Энергия
излучения, или тепловая энергия, которую получает от Солнца 1 см² площади при
перпендикулярном падении солнечных лучей (так называемая солнечная постоянная),
равна на Венере 4 — 4,3 кал/см², т.е. в 1,9 — 2 раза больше, чем на Земле.
Поскольку Венера поглощает лишь 24 — 29% этого количества энергии, в то время
как более темная Земля удерживает 42 — 46% солнечного света, то в конечном счете
Венера получает 0,99 — 1,38 количества энергии, поглощаемого Землей.
Обозначим через QB тепло,
поглощаемое Венерой, а через QЗ —
тепло, поглощаемое Землей; тогда отношение этих двух величин QB : QЗ будет равно от 1,9 · 24 : 1,46 до 2,29 :
1,42.
Правда, Венера в конечном счете не удерживает это количество энергии, тепло
должно вновь излучаться вместе с тем теплом, которое излучает сама планета (это
тепло, как и для Земли, составляет 1/3 ÷ 1/4 от QЗ). Таким образом поверхность Венеры должна
обладать достаточно высокой температурой, чтобы отдавать все это количество
тепла в пространство в виде теплового излучения.
Если плотная атмосфера Венеры содержит много углекислоты, то она должна иметь
гораздо более высокую температуру, чем мы считали до сих пор. Однако,
повидимому, содержание углекислоты в атмосфере Венеры не слишком высоко. На
Венере, как и на Земле, должны существовать области, температура которых может
быть на 40° выше средней температуры планеты. В этих областях безусловно могут
существовать растения (мы знаем виды водорослей, встречающиеся в горячих
источниках, температура которых достигает 60°), которые в короткий срок могут
понизить содержание углекислоты в атмосфере Венеры. Благодаря этому температура
на всей планете в целом может несколько понизиться, так что области, которые
прежде были слишком горячими, могли стать пригодными для развития жизни. Такой
процесс связывания новых количеств углекислоты может продолжаться до тех пор,
пока содержание углекислоты в атмосфере не будет сведено к минимуму.
Существуют вещества, которые видимый свет пропускают хуже, чем тепловые лучи;
к таким веществам относится, например, туман. Белый слой, который мы видим на
Венере, представляет собою, по всей вероятности, не что иное, как туман, и
потому облачный покров Венеры должен быть холоднее, чем это дает вышеприведенный
расчет. Повидимому, среднюю температуру Венеры, если вся ее поверхность имеет
равномерный белый цвет, следует принять равной 8 — 15°С.
Здесь необходимо учесть следующее обстоятельство. Как известно, наша земная
атмосфера наверху очень холодна, но книзу ее температура повышается на 1° на
каждые 200 м. Эту цифру следует принять и для Венеры. Таким образом
действительная поверхность планеты имеет температуру во всяком случае более
высокую; чем слой облаков. Спрашивается, как глубоко лежит под облачным слоем
действительная поверхность планеты. Мы считаем, что на глубине б — 8 км. Во
всяком случае очень странно, что даже в самые сильные телескопы не наблюдается
никаких признаков горных цепей, вершины которых поднимались бы над слоем
облаков. Венера — сравнительно молодая планета и на ней, наверно, как и на
Земле, имеются высокие горы.
В настоящее время мы не знаем, вращается ли Венера вокруг своей оси или она
повернута к Солнцу всегда одной и той же стороной, как Луна к Земле. Скипарелли
является сторонником такого предположения. Другие астрономы, как, например,
Белопольский, считают, что Венера совершает поворот вокруг своей оси за 20 — 36
час.
Климат Венеры должен в очень сильной степени зависеть от того, вращается ли
она вокруг своей оси или нет.
Посещение Венеры может иметь огромный научный и даже философский интерес.
Возможно, что мы найдем на ней те же климатические условия, которые имелись на
Земле, когда на ней зарождалась жизнь. В этом случае мы найдем многое, что нам
поможет ответить на вопросы, связанные с происхождением жизни и развитием
животного мира, — вопросы, на которые не может дать ответа палеонтология, так
как мы не находим окаменелостей, относящихся к этим первым дням жизни.
Собственно говоря, полет на Венеру не представляет особых трудностей. Согласно
(230), требуется vr1 = 2,5 км/сек,
а, согласно (120), идеальная скорость, равная 13 км/сек, вполне достаточна,
чтобы ракета достигла Венеры. Путешествие на Венеру заняло бы самое большее 4 —
5 мес. Точно так же возвращение назад сравнительно легко осуществить; мы имеем в
этом случае vr2 = 3,3 км/сек,
vpB = 10,5 км/сек. Для возвращения
на Землю достаточно идеальной скорости 12,5 км/сек.
Трудности заключаются, главным образом, в посадке на Венеру и в старте при
возвращении на Землю.
Плотная атмосфера Венеры неблагоприятна для полетов ракет для межпланетных
путешествий. Обладая, по всей вероятности, высокой температурой, она делает
почти невозможным хранение топлива в жидком виде, и в настоящее время мы; не в
состоянии сказать, сможем ли мы изготовить топливо на Венере при помощи машин и
какие это должны быть машины.
Напротив, уже при полной идеальной скорости vx < 20 км/сек можно направить ракету по
окружности вокруг Венеры и сфотографировать ее поверхность.
5. Прочие тела Солнечной системы
Остальные небесные тела Солнечной системы являются недостижимыми при помощи
ракет для межпланетных путешествий*.
Например, Меркурий слишком близок к Солнцу, и необходимо было бы преодолеть
разность потенциалов, которая не по силам ракете. Полная идеальная скорость при
полете с посадкой на планету должна была бы быть равной vx = 39 км/сек., а при обращении вокруг планеты
по окружности vx = 38 км/сек. Это
требует минимального отношения масс m0/m1 > 13 200, т.е. число, совершенно
неприемлемое.
Относительно посадки на Юпитер заранее можно сказать, что она невозможна,
хотя бы потому, что он окружен очень плотной атмосферой, имеющей температуру по
меньшей мере 400° С*. О спутниках Юпитера мы в
настоящее время ничего определенного сказать не можем, так как они недостаточно
изучены. Три наиболее далекие планеты (Сатурн, Уран, Нептун) и их спутники тоже
недостижимы.