При падении метеоритов можно наблюдать следующие явления.

1. Метеоритные тела достигают Земли не с космической, а лишь с земной скоростью. Это объясняется тем, что сопротивление воздуха растет пропорционально квадрату скорости и так велико, что небольшие тела могут достичь поверхности Земли лишь со скоростями, не превышающими самое большее нескольких сотен метров в секунду.

2. Метеориты накаливаются при прохождении зоны, лежащей на высоте примерно между 100 и 75 км (вероятно, вследствие того, что их кинетическая энергия превращается в тепло в результате сопротивления воздуха). Упавшие метеориты раскалены по поверхности, внутри же они холодны; на их поверхности видны ясные следы того, что внешний слой был расплавлен и сдут воздухом. Большие метеориты всегда имеют светящийся хвост, который часто можно видеть еще долгое время после того, как сам метеорит уже исчез из вида. Однажды удалось наблюдать хвост, который оставался видимым свыше часа. Цвет этого хвоста соответствовал цвету раскаленных паров железа или раскаленных щелочных металлов. Это позволяет предположить, что хвост состоит из тех же веществ, что и само метеоритное тело, т.е. что он в действительности представляет собою сорванный верхний слой метеоритного тела. Спектроскопическое исследование хвостов является, конечно, исключительно трудной задачей, так как в большинстве случаев они видимы лишь в течение нескольких секунд, и, насколько нам известно, в настоящее время еще нет достаточно надежных спектроскопических исследований метеоритных хвостов.

3. Основываясь на непосредственных наблюдениях, можно утверждать, что светящиеся метеоритные тела имеют температуру от 10 000 до 30 000°. Если бы температура метеоритных тел была ниже, то можно было бы наблюдать лишь метеориты весьма больших размеров и на Землю часто падали бы метеориты различной величины. Кроме того, трудно было бы объяснить, почему в периоды так называемых звездных дождей, которые часто бывают весьма интенсивными, на Землю в большинстве случаев не падает ни один метеорит. С другой стороны, если температура метеоритных тел была бы выше 30 000°, то они светились бы гораздо ярче, чем это наблюдается в действительности. Известен, однако, случай падения метеорита весом 63 кг, который светился так ярко, что его можно было видеть в светлый день. Этот метеорит, несомненно, имел температуру свыше 40 000°.

Указанные температуры представляют собой так называемые эффективные температуры (т.е. температуры, которые должно иметь твердое, абсолютно черное тело при свечении с данной яркостью). Какую же температуру имеют метеоритные тела в действительности, собственно говоря, неизвестно. Можно лишь утверждать, что их действительная температура несколько выше эффективной, но для наших расчетов и не требуется такой точности.

При вычислении температуры, которую достигает воздух на вогнутой стороне парашюта, мы исходим из следующего предположения*. Массе воздуха, которую встречает парашют, сообщается столько тепла и кинетической энергии, сколько кинетической энергии теряет ракета вследствие торможения. При этом необходимо также учесть энергию, излучаемую нагретым воздухом. Если воздушный поток полностью задерживался бы парашютом и не раскалялся бы, то его температуру можно было бы легко вычислить; но нагретый воздух должен излучать много тепла, кроме того, неизвестно, какая часть энергии движения воздуха в действительности теряется. Допустим, что она составляет 99%. Однако это допущение является в высшей степени произвольным. Таким образом приведенный расчет не может ни в малейшей степени претендовать на научную точность.

Можно также исходить из другого предположения, — что при набегании воздушного потока на тело в точках встречи (остановки) воздух нагревается вследствие превращения энергии его движения в тепловую

Как известно, техническая единица массы весит 9,81 кг. Чтобы нагреть 1 кг воздуха на 1°, необходимо затратить 0,24 ккал; 1 ккал соответствует работе 426 кгм. Таким образом, для того чтобы нагреть техническую единицу массы на 1°, требуется 1000 кгм. Если воздух движется со скоростью v, то каждая единица массы обладает кинетической энергией v²/2 кгм. Таким образом набегающий воздух, теряя свою скорость перед телом, нагревается на v²/2000 °С.

В научной литературе часто встречается формула

*

где Т — темепратура снаряда или метеоритного тела, а τ — температура воздуха. Но в применении к метеоритам эта формула дает слишком высокие значения температуры, так как в ней не учитывается поглощение теплового излучения воздухом. Если обозначить температуру метеорита через θ, то по закону Стефана-Больцмана переход тепла для единицы поверхности определится, как известно, формулой

Здесь, коночно, предполагается, что закон Стефана-Болыщана выполняется для паров металлов при θ°.

Рассмотрим абсолютно черное тело, для которого этот закон безусловно выполняется.

По Курлбауму, постоянная σ для абсолютно черного тела имеет следующую величину:

σ = 5,32·10^-12 вт см^-2 град^-4

В наших расчетах можно с достаточной точностью положить σ = 5·10^-12, даже если наше тело будет значительно менее «черным», так как излучающие поверхности больше, чем их проекция в направлении движения; таким образом обе ошибки должны взаимно компенсироваться. Поскольку величиной τ^-4 можно пренебречь по сравнению с θ^-4, то окончательно получим:

S = 5·10^-12 θ^-4 вт см^-2          (177)

Вамслер и Гинлейн нашли для теплообмена между отвесной металлической стенкой и покоящимся воздухом при малых разностях температур следующую формулу:

Q = 3,5·^-4(t - θ) вт см^-2          (178)

где t — температура воздуха, т.е. в нашем случае

Если v очень велико, то можно пренебречь величиной τ и положить t = v²/2000.

Согласно данным, приведенным в справочнике Хютте, теплообмен пропорционален корню квадратному из плотности воздуха, т.е. обратно пропорционален корню квадратному из абсолютной температуры* и прямо пропорционален корнк квадратному из давления воздуха. При больших разностям температур в формулу должен войти еще один множитель, ко торый по Нуссельту пропорционален ⁴√(θ-τ). Однако мы считаем, что этот множитель может появиться лишь при некоторых явлениях в воздушном потоке, которые нас не интересуют, так как в рассматриваемом нами случае не имеют места.

Следовательно, при расчете нагревания метеоритов от встречного потока воздуха необходимо вместо истинного показания барометра брать корень квадратный из этого числа, но, с другой стороны, количество подводимого тепла необходимо положить пропорциональным числу молекул, которые действительно сталкиваются с метеоритом. Если s — высота метеорита над поверхностью Земли, β — давление воздуха на рассматриваемой высоте, а β₀ — давление воздуха у земли, то, согласно (94)

причем Н следует положить равным 7,4 км. Отсюда получим

исло молекул, сталкивающихся с метеоритом, пропорционально скорости, причем среднюю скорость молекул воздуха можно считать равной скорости звука. Поэтому число молекул, ударяющихся о метеорит, летящий со скоростью и, относится к числу молекул, ударяющихся о неподвижную стенку, как √(330² + v²) : 330. При v >> 330 м/сек это отношение можно принять равным v/300.

На этот коэффициент следует умножить правую часть уравнения (178). Наконец, необходимо допустить, что передача тепла обратно пропорциональна корню квадратному из абсолютной температуры, т.е. умножить правую часть нашего уравнения на √288/τ. В результате получим:

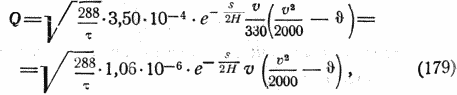
где θ — абсолютная температура метеорита.

Для того чтобы определить, как сильно нагреется метеорит, необходимо приравнять величину Q из этой формулы величине S из формулы (177), и тогда получим:

Если применить эту формулу для определения температуры метеорита, летящего со скоростью 36 км/сек, то получим значение, в 5 — 7 раз меньшее действительного.

Отсюда можно заключить, что передача тепла должна быть значительно больше, чем мы приняли (примерно в тысячу раз), и правую часть формулы необходимо умножить еще на коэффициент, который при 0° равен единице, а при θ = 20 000° равен 1000. В качестве простейшего коэффициента такого вида кожно предложить выражение (θ—253°)·1/20. Но для промежуточных значений θ этот коэффициент, вероятно, слишком велик и целесообразнее было бы подобрать выражение, которое вначале, как в формуле Нуссельта, пропорционально корню четвертой степени из t°, а затем начинает расти быстрее, так что при t = 20 000° оно принимает значение 1000. Однако мы считаем, что наши расчеты не нуждаются в такой точности.

Так как в действительности мы можем сказать лишь кое-что о наблюдаемых излучениях, а об истинной температуре метеоритных тел мы не делали никаких предположений, то следует заключить, что & есть эффективная температура, т.е. та температура, которую должно было бы иметь абсолютно черное тело, светящееся с яркостью ;метеорита. Но эта температура и нужна, так как мы хотим лишь знать, какое количества тепла излучается или, вернее, какое количество тепла было-приобретено. В таком случае

При той небольшой точности, с которой производились наши расчеты, можно положить

Тогда получим:

или

Как уже было упомянуто, множитель (θ—253°)·1/20 несколько велик для ракетных скоростей, и получающуюся ошибку можно несколько скомпенсировать, если в последней формуле опустить множитель ³√5.

Тогда получим:

Поскольку θ есть эффективная температура, то теплоотдача через излучение определяется по формуле S = σθ⁴ и тепло Q, приобретенное вследствие трения, должно быть примерно равно этой величине.

Если плоскость расположена к воздушному потоку под углом α, то для значений углов между 45 и 90° число ударяющихся о плоскость молекул пропорционально приблизительно величине sin α; то же относится, конечно, и к приобретению тепла, и потому мы должны в этом случае положить Q = σθ⁴ sin α. Ошибкой, которую мы при этом, вероятно, совершаем в отношении величины α, можно здесь пренебречь. Если же плоскость движется по направлению полета, то число молекул воздуха, ударяющихся о нее, так относится к первоначальному числу, как скорость звука к скорости v. Для передачи тепла мы в этом случае получим Q' = Q330/v (скорость звука полагаем равной 330 м/сек; действительную же величину скорости звука в верхних слоях атмосферы можно определить лишь при помощи регистрирующих ракет; но если примем 330 м/сек, то ошибка не будет слишком большой, во всяком случае она не скажется сильно на результатах расчета). Для углов от 0 до 45° можно положить

Если выразить α в радианной мере, то

Если же α выразить в угловой мере, то

При этом

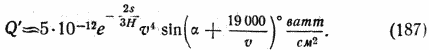
Это, конечно, лишь очень грубая оценка. Результат может оказаться в 10 раз больше или меньше действительного значения; но он дает по крайней мере некоторое представление о порядке величины теплопередач, с которыми нам придется иметь дело.

Температура неохлажденной поверхности, расположенной под углом α к воздушному потоку, при скоростях 5000 — 15 000 м/сек может быть определена по формуле

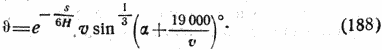
Приведенные выше формулы выводились так подробно лишь потому, что они, по нашему мнению, дают результаты, приближающиеся к действительности больше, чем все известные нам формулы. Существует еще теория, которая на основе термодинамических и физико-химических соображений пытается по числу и силе соударений молекул определить возникающие при этом колебания молекул метеорита. Но результат вычислений по этой теории получается больше примерно в 100 раз. Даже в предположении наличия чистой водородной атмосферы* этот результат был бы слишком велик.

Таким образом искомая температура значительно превышает для ракет 5000°. Если же необходимо предотвратить такое сильное нагревание поверхности, следует подвести достаточное количество охлаждающего вещества, чтобы оно могло отнять тепло Q'.

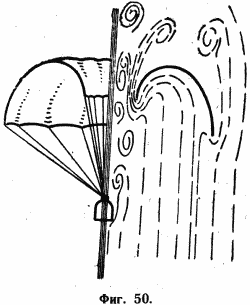
Несмотря на высокую температуру θ теплопередача не слишком велика. При помощи, например, водяного охлаждения можно отнять у металлической стенки гораздо большее количество тепла. Как говорят в теплотехнике, мы имеем здесь дело с нагреванием, высоко эффективным в качественном, а не в количественном отношении. Относительно расхода охлаждающего вещества можно сказать следующее: стремление к экономии охлаждающего вещества может быть удовлетворено, если воздушный поток будет встречать на своем пути вогнутые поверхности (фиг. 50). Если навстречу воздушному потоку движутся косые или выпуклые поверхности, то слой воздуха, охладившийся до температуры стенки, будет постоянно уноситься потоком; кроме того, мы не можем нагреть охлаждающее вещество до температуры выше допустимой для стенки. Предположим, что в качестве охлаждающего вещества применяется лед, над которым пропускается уже нагретая вода охлаждения так, чтобы сначала лед растаял, а затем вся образовавшаяся вода испарилась. Далее пар пропускается вдоль охлаждаемых стенок, и выпускается в атмосферу, когда он приобретает максимальную температуру, допустимую для стенок. Таким способом можно при помощи 1 кг льда отобрать 750 ккал. Напротив, если этот пар (см. фиг. 50) выпустить в полость парашютообразно изогнутой поверхности, то благодаря соударению с молекулами воздуха пар будет продолжать нагреваться. Если направление воздушного потока не сильно отклонено от оси парашюта, то воздух не будет в состоянии сдуть паровую завесу и только под действием последующих порций пара этот слой выйдет за края парашюта. При этом температура перетекающего пара будет лишь очень немногим меньше температуры, которую должен иметь воздух в таком полом парашюте. При скорости 10 000 м/сек эта температура, безусловно, превышает 15 000°. Вероятно, она даже превышает 20 000°. Но при такой температуре 1 кг водяного пара с учетом диссоциации поглощает свыше 9000 ккал, т.е. в 12 раз больше, чем при косых или выпуклых поверхностях. В то же время такое колоссальное нагревание пара в полом пространстве парашюта не должно нас пугать. Слой пара, находящийся позади раскаленного переднего слоя, сам по себе представляет максимально эффективную защиту от передачи тепла куполу парашюта.

Установив эти основные положения, посмотрим, можно ли использовать (силу торможения от сопротивления воздуха для обеспечения посадки ракет.

Прежде всего отметим, что эта проблема не является одной из решающих. Можно было бы сконструировать ракеты, способные частично тормозить свою скорость при помощи реактивной силы еще вне пределов земной атмосферы. Но в этом случае отношение m₀/m₁ должно быть в 20 — 40 раз больше, т.е. для торможения ракеты реактивной силой мы должны начальный вес ее увеличить в 20 — 40 раз при прежней полезной нагрузке.

Ракеты без людей могут спускаться в любом направлении. Но ракеты с людьми не должны, конечно, падать на землю отвесно, так как в этом случае участок торможения будет слишком мал. Но поскольку ракета с людьми и без того должна обладать некоторым боковым движением, если подъем ее совершался по синэргической траектории, то она будет приближаться к Земле по некоторой кривой второго порядка; можно добиться того, чтобы ближайшая к Земле точка этой кривой находилась в верхних слоях атмосферы. Даже если слой атмосферы, в которой возможно действие парашюта, составляет 7 км (выше воздух слишком разрежен, а ниже путешественникам угрожает эффект сильного торможения) и если ракета приближается к Земле по параболической орбите, участок торможения или, точнее, путь, пройденный в упомянутом выше слое, составляет более 800 км.

Это можно доказать следующими расчетами. По уравнению параболы в полярных координатах

где ρ — радиус-вектор, φ — полярный угол, р — параметр параболы.

Если h — толщина воздушного слоя, в которэм может совершаться торможение, и r — радиус Земли, то при

и для ρ = r получим

cos φ = 1 и φ = 0

а для ρ = r + h

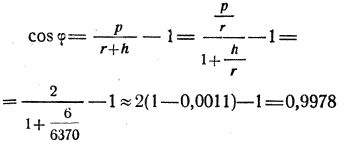
и

φ = ±3,8°

Участок пути, на котором совершается торможение, составит

s = 2·φr = 840 км

На всем этом пути параболическая скорость ракеты тормозится до эллиптической. Затем ракета снова проходит через наиболее близкую к Земле точку в том же месте атмосферы, причем участок торможения будет еще длиннее, так как эллипс еще более подходит к, окружности и т.д. При этом наиболее близкая к Земле точка не будет сколько-нибудь существенно приближаться к Земле. Так будет продолжаться, пока не будет достигнута круговая скорость. При круговой скорости участок торможения будет бесконечно велик и ракета для межпланетных путешествий сможет спуститься по достаточно длинной спирали.

Для достижения этой цели мы стремились сконструировать ракету так, чтобы воздушному потоку были противопоставлены лишь вогнутые поверхности (за исключением нескольких расчалок, которые, естественно, должны особенно эффективно охлаждаться). Так как собственно поверхность ракеты имеет лишь одну такую вогнутую часть, а именно — дно с соплами, то необходимо добиться, чтобы это дно ракеты шло вперед. Этого можно достигнуть, если, как показано на фиг. 50, укрепить парашют на головной части ракеты. Торможение является, конечно, лишь второстепенной задачей этого парашюта; основная же состоит в том, чтобы при посадке ракета двигалась дном вперед. Остаточную скорость в 80 м/сек этот парашют вообще не может затормозить, и она должна быть поглощена при помощи реактивной силы. Конечно, далеко не безразлично, затормозить ли при помощи реактивной силы скорость 80 м/сек или 11 км/сек.

Вогнутая поверхность парашюта должна охлаждаться льдом, водой или водяным паром. За ракетой образуются воздушные вихри, которые, конечно, могут легко сдуть в сторону слой водяного пара перед парашютом, и парашют то там, то здесь может притти в соприкосновение с воздушным потоком, нагретым до температуры свыше 20 000°. С целью воспрепятствовать этому необходимо делать парашют кольцеобразным, чтобы воздушные вихри его не касались. Такой парашют был нами предусмотрен для первых (регистрирующих) ракет, так как, во-первых, регистрирующие ракеты вообще не могут приземлиться иначе, как на парашюте, во-вторых, еще слишком мало известны затронутые здесь вопросы теплопередачи.

Если наши регистрирующие ракеты покажут, что весь рассмотренный нами процесс происходит более благоприятно, чем мы ожидали (мы рассчитываем всегда на наиболее неблагоприятные условия), то можно будет подумать и о других способах приземления.

Валье, Гоман, Гайль, Цандер и Циолковский полагают, что ракета для межпланетных путешествий будет сконструирована, подобно самолету, и при возвращении на Землю она сможет приземляться в планирующем полете.

Наиболее целесообразную высоту s по отношению к земной поверхности для точки траектории, ближайшей к Земле, можно найти из следующих соображений.

Допустим, что планирующий полет рациональнее всего происходит в спокойном воздухе при нормальном давлении и скорости 108 км/час = 30 м/сек. Если ракета для межпланетных перелетов входит в атмосферу со скоростью не 30 м/сек, а 9000 м/сек, то для сопротивления воздуха справедлива приведенная нами формула (27). Отсюда получаем:

*

Здесь β_S означает давление воздуха на рассматриваемой высоте, β₀ — нормальное воздушное давление. Очевидно, самолету рациональнее всего лететь со скоростью 9000 м/сек тогда, когда L₃₀ = L₉₀₀₀, откуда следует

β₀/β_S = 135 000

Согласно формуле (34), значение s, при котором давление воздуха уменьшается до 1/135 000 составляет

S = 87 км

Приведенный расчет является, конечно, приближенным, так: как H в действительности не является постоянной величиной. Точную зависимость между β и s необходимо будет установить при помощи регистрирующих ракет или реактивных самолетов.

Для того чтобы аппарат дольше находился на желаемой высоте, можно, как предлагает Гоман, расположить крылья так, чтобы они вначале прижимали ракету книзу, для того чтобы она не смогла под действием центробежной силы вновь, оторваться от Земли.

Идея приземления на планирующем полете сама по себе имеет много подкупающего.

1. Спуск на планирующем полете обеспечивает водителю ракеты большую свободу выбора места для посадки. Например, если межпланетная ракета попадает в земную атмосферу с параболической скоростью, то она должна пролететь на планирующем полете 20 000 км, пока ее скорость не затормозится. Но при планирующем полете она сможет описывать любые кривые и водитель в состоянии приземлиться в избранном им месте. Правда, при параболической скорости возможность маневрирования невелика, так как эффект ускорения, вызванного центробежной силой на кривых с радиусом кривизны менее 6000 км, станет совершенно невыносимым. Радиус кривизны уменьшается пропорционально квадрату скорости. Например, при скорости 5 км/сек необходимый радиус кривизны становится всего лишь 1240 км. Под конец межпланетная ракета может описывать сужающуюся спираль и приземлиться точно у цели. Не существует такого пункта на Земле, который был [бы ракете недоступен, независимо от того, в каком месте она вступила в пределы земной атмосферы.

Необходимо также иметь в виду то, что число 20 000 км мы получили, принимая, что круговую скорость ракета получит на той же высоте, на которой лежит ближайшая к Земле точка космической орбиты. Но это не является обязательным.

При посадке при помощи парашюта выбор места приземления более ограничен. Можно, правда, несколько подтягивать стропы парашюта с определенной стороны, что дает возможность выбрать место посадки в радиусе 1000 — 2000 км. Но зтого совершенно достаточно, тем более, что (как и при посадке с несущими поверхностями) существует возможность путем соответствующего выбора орбиты в межпланетном пространстве перенести посадку в любое необходимое место. Если, например, предпринимается полет по эллиптической орбите, то необходимо лишь несколько иначе расположить эллипс, чтобы приземлиться в другом месте и в другое время.

Таким образом и в том и в другом случае можно приземлиться в любом желаемом пункте. Преимущества посадки при помощи несущих поверхностей будут особенно важны в случаях, когда орбита в межпланетном пространстве была выбрана неправильно, когда ракета по какой-либо причине сошла со своей орбиты или же когда ракета, уже вернувшись в земную атмосферу, против ожидания снова вырвется из нее и опишет одним эллипсом торможения больше, чем предполагалось. Приземление в последнем случае при помощи парашюта может происходить в такой области, которая в радиусе 1000 км непригодна для посадки или же по меньшей мере не сплошь пригодна (точное управление посадкой в этом случае исключается). Таким местом может оказаться южная часть Тихого океана, Тибетское плоскогорье или же полярные области.

Наконец, преимущества посадки при помощи несущих плоскостей будут иметь большое значение также и в том случае, когда выбор места посадки на Земле не вполне свободен (например, в случае возвращения ракеты с какой-либо планеты).

2. Приземление при помощи несущих поверхностей, вообще говоря, не ставит таких высоких требований к подготовке водителя, как приземление при помощи парашюта. На аппарате с крыльями он может достичь большинства пунктов в простом планирующем полете; лишь в переходных областях необходимо умение водителя, превышающее простой инстинкт. Далее, если водитель вначале допустил ошибку в управлении, то впоследствии он в большинстве случаев может ее исправить, так как управляемость все увеличивается. При такой посадке он просто летит, как на самолете, по тому направлению, которое ему нужно. Поскольку он видит под собой значительную часть земного шара, то он, конечно, совершенно точно видит, где находится место, в котором он предполагает приземлиться. Долетев до этого места, он начинает спускаться по спирали.

Напротив, при посадке при помощи парашюта водитель не должен ни на минуту не ослаблять своего внимания, малейшая небрежность может поставить на карту успех всего полета. Траектория в межпланетном пространстве также должна быть более точно вычислена. Конечно, все это может быть достигнуто, но все же приземление с несущими поверхностями имеет преимущества.

3. При нормальном приземлении при помощи крыльев со скоростями, меньшими круговой, ракета сама находит ту высоту, на которой полет наиболее выгоден. Например, если ракета спускается слишком низко, то растет сопротивление воздуха и вместе с тем и подъемная сила, при этом ракета снова поднимается. Вообще можно работать над тем, чтобы управление во время полета по инерции в основном осуществлялось автоматами, в то время как в ракетах, посадка которых должна происходить при помощи парашюта, водитель (находясь к тому же под сильным воздействием повышенного опорного ускорения) все время должен наблюдать за управлением.

4. Посадка при помощи крыльев, вообще говоря, приятнее для людей, находящихся в ракете. Как правило, путешественники в этом случае никогда не подвергаются эффекту опорного ускорения, существенно превышающего нормальное ускорение силы тяжести на Земле.

Приземление при помощи парашюта протекает вначале также вполне гладко. Но при скоростях между 6000 и 2000 м/сек опорное ускорение должно быть при всех условиях сильным. Вначале под действием центробежной силы ракета как бы парит в воздухе, но при скорости ниже 6000 м/сек эта сила заметно ослабевает и ракета быстро попадает в более плотные слои атмосферы. Когда она еще располагает скоростью 2000 м/рек, она летит на высоте 50 км. Только начиная с этой высоты, она может свободно следовать действию силы тяжести.

5. Само приземление для крылатой ракеты много проще. Ракета же с парашютом падает, достигая в конце концов скорости 80 м/сек; при этой скорости водитель должен незадолго до достижения Земли (точнее — водной поверхности, на которую спускается), т.е. на высоте 100 — 150 м, дать еще раз газ, чтобы погасить и эту последнюю скорость. При этом ракета может спускаться только на воду. Если двигатель не запустится или водитель по какой-либо причине опоздает пустить его в ход, то это, хотя и не будет стоить путешественникам жизни, все же может вызвать разрушение части конструкций (нельзя забывать, что водитель после тяжелого и напряженного межпланетного путешествия, находясь к концу торможения под эффектом опорного ускорения, равного 40 м/сек², по всей вероятности, не обладает нормальной сообразительностью и способностью принимать быстрые решения). Напротив, посадка аппарата с несущими плоскостями происходит так же, как посадка самолета.

6. Для осуществления посадки при помощи парашюта в заданном пункте необходимо ближайшую к Земле точку космической орбиты (относительно земной поверхности) определять с точностью до 5 км. Если мы хотим приземлиться вообще, безразлично где, то при гиперболической орбите нужна точность до 15 км. Если ближайшая к Земле точка будет выбрана слишком высоко, то воздух не сможет достаточно эффективно затормозить аппарат, и он снова вырвется из сферы притяжения Земли. Если эта точка будет слишком низко, то торможение будет резкое и возникающее опорное ускорение может раздавить людей, находящихся в ракете. При эллиптических скоростях достаточно, если ракета вообще лишь задевает земную атмосферу и не проникает в нее слишком глубоко. В этом случае она будет описывать все более узкие эллипсы торможения и, наконец, где-нибудь приземлится.

Но если высота будет больше, чем нужно, всего лишь на 20 км, то предсказать точку приземления невозможно.

Напротив, посадка с несущими поверхностями происходит вполне гладко, даже при гиперболической скорости и даже в том случае, если ошибка в высоте составляет до 22 км кверху или до 20 км вниз. Несущая плоскость, будучи сильно наклонена, может нести в 5 — 8 раз больше того, что она несет при наиболее благоприятном положении. Поэтому, например, если ракета попадает в воздушный слой, разреженный в восемь раз более, чем ожидалось, т.е. если высота будет на 15 — 16 км больше, чем нужно, то, наклонив головную часть ракеты вниз, можно добиться появления прижимающей ее к Земле аэродинамической силы, т.е. того, чтобы она осталась в атмосфере и не вылетела снова из нее. При этом лобовое сопротивление также сильно растет, но это приводит лишь к торможению, так что гиперболическая скорость вскоре переходит в эллип-тяческую (при этом мы, конечно, говорим лишь о таких гиперболических скоростях, которые доступны межпланетным ракетам, т.е. 12 — 17 км/сек). Если, напротив, орбита будет нацелена слишком низко, то ось ракеты надо будет расположить таким образом, чтобы аэродинамические силы не действовали вниз.

Торможение сопротивлением воздуха на правильно выбранной высоте составляет около 2 м/сек². Но человек выносит опорное ускорение более, чем 40 м/сек². Таким образом ракета может лететь в воздухе, в 20 раз более плотном, и действие опорного ускорения не будет угрожать людям, другими словами, — ближайшая к Земле точка может лежать на 20 км ниже. Это дает для высоты, на которой может лежать ближайшая к Земле точка, интервал в 40 и и более. При этом, если даже ракета один раз и вырвется против ожидания из заданной траектории, то благодаря управляемости ракеты будет сохранена возможность достижения желаемого места посадки.

Конечно, в принципе посадка при помощи парашюта возможна, в противном случае мы не стали бы рассматривать этот способ в книге, целью которой является доказательство, что полет ракет в межпланетное пространство — не есть утопия. Посадка при помощи парашюта будет лишь значительно более трудной и сложной, чем посадка с несущими поверхностями. Несмотря на это, мы все же предлагаем посадку при помощи парашюта, а не посадку с несущими плоскостями, из следующих соображений.

В этой книге мы хотим доказать, что наш проект выполним при всех обстоятельствах, а это справедливо лишь при посадке при помощи парашюта. При посадке с использованием крыльев существует опасность, что нагревание ракеты будет слишком велико, хотя и нельзя сказать, чтобы эта опасность была весьма вероятной. Если, например, применить выведенную нами формулу, то мы получим вполне приемлемые цифры, но, как уже было указано, формула не является точной и результат может оказаться в 100 раз больше. В этом случае посадка с несущими поверхностями была бы невозможна.

Если даже допустить, что это огромное количество тепла удастся отвести при помощи водяного охлаждения (в чем мы также не можем быть уверены) и что при этом металл не прогорит, а при водородном охлаждении не возникнут трещины и разрывы из-за сильного одностороннего охлаждения, то необходимо все же иметь в виду, что масса воды, которая потребуется для охлаждения, будет больше, чем масса топлива, необходимого для торможения космической скорости при помощи реактивной силы.

Весьма многообещающим кажется нам предложение Гомана приделать парашют к хвосту корабля, снабженного крыльями. Тогда ближайшая к Земле точка космической орбиты не должна лежать так низко, так как парашют достаточно сильно тормозит уже на большой высоте, а крылья сравнительно мало нагреваются в разреженном воздухе. Мы считаем, что таким способом нагревание ракеты можно уменьшить в 100 раз по сравнению с тем, каким оно было бы, если бы ракета спускалась без парашюта. Для этого парашют должен испытывать в 100 раз большее сопротивление воздуха, чем ракета, имеющая форму обтекаемого тела, а этого нетрудно добиться.

Таким образом вплоть до достижения круговой скорости тормозит, главным образом, парашют, а при скорости, меньшей круговой, могут быть использованы также и крылья, что-бы дольше удержать корабль на необходимой высоте. При скорости полета, близкой к круговой, нагрузка на несущие поверхности очень невелика, так как ракета при этом как бы не имеет веса. Напротив, когда скорость становится ниже круговой, нагрузка на несущие поверхности увеличивается все больше, но при этом нагревание быстро уменьшается.

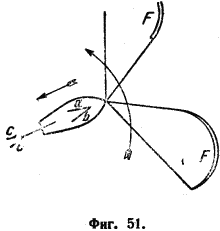
Такой способ посадки, по всей вероятности, оказался бы возможным и объединил бы главнейшие преимущества посадки при помощи парашюта и посадки с крыльями. Нечто подобное можно предусмотреть для нашей модели Е, а именно — кабину наблюдателя можно снабдить несущими поверхностями и устроить таким образом, чтобы она могла отделиться от ракеты и спуститься самостоятельно в планирующем полете, в то время как ракета приземлялась бы при помощи парашюта. Другая возможность объединить преимущества обоих способов посадки изображена на фиг. 51. Ракета имеет тело — относительно длинное, несущие поверхности а и b и хвостовые стабилизатора с — с. Обе половины стабилизатора и несущих поверхностей соединены на ребре друг с другом при помощи воздухонепроницаемого резинового соединения.

Овальный, сравнительно небольшой парашют F — F находится в головной части ракеты, так что ракета движется соплом вперед. Несущие поверхности и хвостовые стабилизаторы не сложены и образуют полые поверхности, встречающие воздушный поток. Когда скорость падает ниже 7000 м/сек, жертвуют парашютом, хвостовые стабилизаторы с — с складываются вместе и поверхность b накладывается на а. Затем ракета опрокидывается (в направлении, показанном стрелкой) и летит дальше в планирующем полете головной частью вперед.

Все сказанное выше относилось к посадке ракеты с людьми. Для ракеты без людей возможна, конечно, лишь посадка при помощи парашюта.

Вообще говоря, очевидно, еще преждевременно много писать о способах посадки. Целесообразнее было бы исследовать вопросы нагревания при помощи регистрирующих ракет и ракетных самолетов и после получения интересующих нас величин подумать, как лучше всего осуществить посадку ракет с людьми.

Далее...