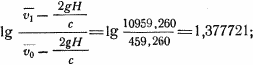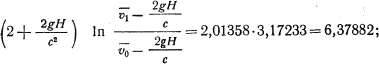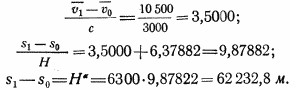Можно написать

mdvx + cdm = 0

[сравните с (5)].

Будем рассматривать ракету, поднимающуюся в атмосфере. Подъему противодействуют сопротивление воздуха и вес ракеты. Таким образом dvx > dv. Можно сказать, что dvx = dv + dq и v = vx — q [ср. с (9)].

Если обозначить силу, противодействующую подъему ракеты, через Q, то очевидно, что

dq / dt = Q / m

и

В нашей записи величина dq имеет знак, совпадающий со знаком Θ, которое всюду считается величиной положительной. Следует одиако иметь в виду, что q — замедление, направленное против v.

Для каждой ракеты имеется определенное значение скорости, обозначаемое через v, при котором q будет минимальным. Ракета, совершающая медленный полет, вынуждена слишком долго противодействовать силе тяжести. Однако при слишком быстром полете воздух будет оказывать очень большое сопротивление.

Таким образом, исходя из необходимости получить наименьшее сопротивление воздуха, желательно совершать медленный полет, а имея в виду гравитационные силы, желательно добиться быстрого полета. Между этими двумя противоположными требованиями может быть найдено такое компромиссное решение: существует такая скорость полета, при которой сумма замедлений q будет минимальной; эту скорость назовем наивыгоднейшей и обозначим v.

Рассмотрим полет ракеты со скоростью v по прямой через слой воздуха толщиной dh на высоте h от поверхности земли. Пусть при этом количество движения ракеты увеличится на заданную величину m · dv. Масса ракеты при этом уменьшится, конечно, на величину dm. Если же ракета пролетает слой воздуха dh с несколько измененной скоростью v + dv, то при сохранении угла подъема α, толщины слоя воздуха dh и приращения количества движения mdv расход горючего будет уже несколько иным. Варьируя скорость полета, можно выбрать ее такой, чтобы dm стало минимальным. Из выражений (9) и (20) следует:

-dvx + dv + Q/m · dt = 0

или

-mdvx + mdv + Qdt = 0

И так как, согласно (4),

—mdvx = cdm,

то

cdm + mdv + Qdt = 0      (21)

При угле подъема α

Подставляя (22) в (21), получим

Согласно условию, величины dh, sin α и mdv являются постоянными. Величина с также принята постоянной. Таким образом при дифференцировании по v получим

Очевидно, что dm будет минимальным, если

В этом случае должно также выполняться условие

Q представляет собой сумму двух сил, из которых L — сила сопротивления воздуха, a G — доля силы тяжести ракеты, противодействующая подъему. Величину ускорения силы тяжести g в целях упрощения расчетов принимаем для атмосферы постоянной, тогда вес ракеты будет равен mg. В случае, когда ракета подымается под углом α, вес ее может быть разложен на две слагающие: mg sin α — по направлению движения и mg cos α — перпендикулярно ему.

Дальнейшие расчеты зависят от тех предположений, которые мы принимаем в отношении величины α.

Точность наводки ракеты при автоматическом управлении будет наибольшей, как мы в этом убедимся в дальнейшем в гл. VIII, если ракета летит по прямой, т. е. если угол α. выдерживается в полете постоянным. В этом случае слагающую mg cos α надо компенсировать силами, возникающими при повороте оси ракеты на некоторый угол относительно направления полета. Угол между направлением полета и осью ракеты можно обозначить через δ. Такое наклонное положение ракеты приводит к некоторой потере тяги, так как появляется боковая сила, и на ракету действует не импульс cdm (в направлении полета), а импульс cdm cos δ. Но так как величина cos δ очень близка к единице, а неточность в установлении величины с больше (1 — cos δ), то этой потерей тяги можно пренебречь, тем более, что она сопровождается увеличением cos δcdm/dt. Кроме того, при наклонном положении оси возникает аэродинамическая подъемная сила, которая должна компенсировать составляющую mg cosα — sinδ cdm/dt. С подъемной силой связано и лобовое сопротивление kmg cosα*. В настоящее время проводятся систематические исследования для установления величины коэффициента k — отношения лобового сопротивления к подъемной силе при сверхзвуковых скоростях полета.

На основании наблюдений при стрельбе снарядами можно уже сейчас сказать, что величина k составит примерно 1/3 - 1/6.

Таким образом*

G = mg (sinα + kcosα)     (26)

Сила сопротивления воздуха L определяется формулой*

L = Fγβv²     (27)

где F — наибольшее поперечное сечение ракеты;     γ — балистический коэффициент сопротивления.

Внешняя форма ракеты, в особенности ее головной части, аналогична форме немецких снарядов S, для которых кривая значений γ (по Кранцу и Беккеру) имеет вид, показанный на фиг. 20.

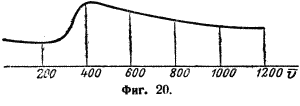
Абсолютные значения γ нас пока не интересуют. По приведенной кривой можно установить, что при скоростях до 300 м/сек величина γ остается примерно постоянной; при достижении скорости звука значение γ сильно возрастает, достигая максимума (примерно в 2,6 раза больше значения при дозвуковой скорости) при скорости 425 м/сек. После этого у асимптотически приближается к величине, примерно в 1,5 раза большей величины γ при дозвуковых скоростях полета. Аналогичные кривые получили Роте, Крупп, Эбергардт и Сиаччи для артиллерийских снарядов. Другие авторы пришли к подобной форме кривой из теоретических соображений.

Какова же причина того, что значение у сначала растет, а затем снижается?*

Рост γ в области скоростей между 300 и 400 м/сек объясняется весьма просто. Если снаряд движется со скоростью, меньшей скорости звука, то уплотнение воздуха перед его головкой выравнивается тем, что воздух движется в стороны, и тем, что в силу упругости воздуха уплотнение его передается вперед. Когда v больше скорости звука, возможно лишь движение воздуха в стороны, а при этом, естественно, уплотнение воздуха перед снарядом увеличивается. Действие этого уплотнения воздуха, которое оно оказывает как при дозвуковых скоростях, так и при сверхзвуковых, пропорционально квадрату скорости.

За снарядом получается пространство с разреженным воздухом, воздействие которого (подсос) вначале также возрастает пропорционально квадрату скорости. Но при скорости, равной скорости звука*, наступает предел, потому, что больше, чем до абсолютного вакуума, воздух за снарядом не может разрежаться, и быстрее, чем со скоростью звука, он не может смыкаться за снарядом. Таким образом при высоких скоростях доля подсоса в общем сопротивлении воздуха все больше уменьшается по сравнению с давлением на головную часть. Отсюда следует, что балистический коэффициент, равный

асимптотически приближается к величине

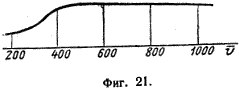
Во время работы ракетного двигателя действие подсоса вообще отпадает, так как пространство за ракетой заполняется вытекающими из двигателя газами. В этом случае изменение γ происходит примерно, как это показано на фиг. 21. В начале γ имеет постоянную величину, затем увеличивается в области скоростей между 300 и 400 м/сек, а при высших скоростях становится опять почти постоянной.

Таким образом в областях скоростей ниже 300 и выше 460 м/сек величину γ можно считать постоянной, а между 300 и 460 м/сек ее значение можно интерполировать по среднему участку параболы третьей степени. Так как для хороших конструкций ракет vo > 500 м/сек, то коэффициент γ вообще можно считать постоянным.

Из равенства

с учетом выражений (26) и (27) получим:

*

где β — плотность воздуха — в рассматриваемом случае принимаем неизменяющейся (мы сопоставляем здесь различные значения v).

Таким образом получим выражение

которое равно нулю при

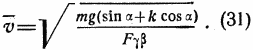
В этом случае

В последнее время часто предлагалось увеличить высоту подъема ракеты путем снабжения ее несущими поверхностями и подъема ее под малым углом. При этом G, конечно, уменьшится и L может быть вследствие этого также малым. Против этого можно сделать следующие возражения.

Согласно (20)

Так как v является оптимальной скоростью для каждого угла α, то при других скоростях ракета будет подниматься хуже.

Если подставить из (32) Q = 2G и значение v из (31), то получим:

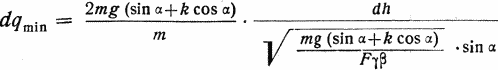
или

Это выражение дает потерю скорости dq при пролете слоя dh и показывает, что она является минимальной, если α = 90°, так как в этом случае

в то время как при других α

Более подробно наивыгоднейшие траектории будут рассмотрены в разделе, посвященном «синэргаческим» траекториям.

Там мы увидим, что в выражении для G отпадет член kmg cos α, который единственно обусловлен требованием соблюдения прямолинейности траектории.

В этом случае

Q = Fγβv² + mg sin α

откуда

Подсчет показывает, что и здесь Q = 2G, но оно меньше по величине, чем при прямолинейной траектории, так как G имеет меньшее значение. Кроме того, в этом случае преимуществом является то, что ракета как раз в начале полета, т.е. в плотной атмосфере, летит более круто, чем это требуется после окончания работы двигателя.

С точки зрения дальности полета такой подъем следует предпочитать; для больших ракет он будет, вероятно, применяться как правило, но для малых ракет это связано с необходимостью весьма сложного устройства управления. Надо сказать, что v является оптимальной скоростью в точке траектории s, но v не будет обязательно оптимальной, если иметь в виду весь подъем ракеты*.

Пусть vo будет значением v для начального мгновения на высоте s. Эту скорость ракета получает от постороннего источника энергии. Очевидно, что v должно быть по возможности большим, а расход горючего — малым, чтобы внешнее давление воздуха β и тем самым и сила L убывали быстрее, чем расходуется топливо. При этом v будет увеличиваться и ракета на какой-то высоте s, достигнет скорости v1. Пусть горючего ракеты хватает как раз на то, чтобы достичь S1 и иметь там скорость v1 тогда ракета достигнет, скажем, максимальной высоты S2. Если же она получит скорость v1 раньше, то увеличенное сопротивление воздуха затормозит ее, и тогда она не будет больше иметь скорости v1 на высоте s1 и, следовательно, не достигнет s2. Если же ракета не достигла еще скорости v1 на высоте s1, то она вынуждена слишком долго преодолевать действие сил тяжести и снова не дойдет до s2.

Если значения vo, s1 и v1 даны, то оптимальная скорость между значениями vo и v1 обозначенная vg, будет соответствовать минимуму

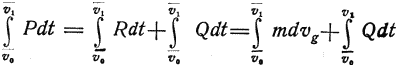
∫Qdt имеет минимум при скорости, равной v, так как при этом все Qdt являются минимальными [см. (23) и (25)], но mdv, наоборот, будет минимальным, если ускорение вначале равно нулю и скорость будет нарастать лишь, когда значительная часть топлива израсходована.

Следовательно, vg в нижней части пути меньше v и разность между ними остается постоянной, но на высоте sx скорость vg быстро достигает v. Разность v — vg можно найти как функцию s. Например, для случая vo = 500 м/сек в атмосфере разница достигает 200 м/сек (для v1 = 2000 м/сек). Разница будет тем меньше, чем больше величина с. При увеличении v относительная разница уменьшается, а абсолютная растет (например, при v1 = 10 000 м/сек она будет для приведенного примера равна 250 м/сек). Выигрыш скорости составит здесь 10,3 и соответственно 12,5 м/сек.

Неточности, неизбежные в расчетах, значительно больше этих величин (в основном потому, что недостаточно точно дано значение с). Кроме того, отклонение от vg,обусловленное причинами технического порядка, тоже больше v — vg.

Дальнейшие выводы приведем сперва для случая, когда скорость всюду равна v, так как при этом формулы значительно упрощаются.

Для подъема по прямой линии имеем из (31):

Плотность воздуха β является функцией высоты s (s = ∫vdt). В верхних слоях атмосферы точное значение β неизвестно, но оно и не требуется, как это будет показано ниже. Для нижних слоев плотность β может быть достаточно точно подсчитана по барометрическим формулам, приводимым в учебниках метеорологии. Но если применить эти формулы, то мы придем к уравнениям, которые не интегрируются в элементарных функциях. Поэтому применим здесь следующий метод расчета.

Примем

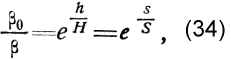
где Н — постоянное расстояние, принимаемое в первом приближении равным 7,5 км, a S = H cosecα.

Следовательно,

и

После дифференцирования (35) получим:

Из уравнения (23) следует:

Из уравнений (32) и (26) получим:

а из (36), (23) и (35а)

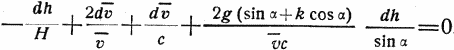
Имея в виду, что dh = v sin α dt и что Н/sin α = S представляет собой не что иное, как путь, который нужно пройти для того, чтобы давление воздуха понизилось в е раз, а также, наконец, и то, что секундную потерю скорости ракетой из-за сопротивления воздуха или из-за действия силы тяжести (здесь они равны друг другу) можно выразить через

r = g · (sin α + k · cos α)

то наша формула запишется так:

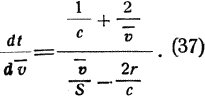
Отсюда после интегрирования определится зависимость между оптимальной скоростью и временем:

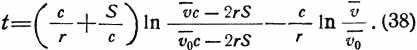
Примечание. При расчете по счетной линейке вычисления удобно вести, определив

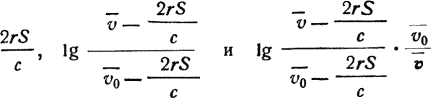
и тогда

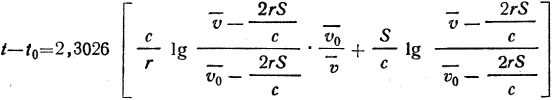
При подстановке в уравнение (38)

voc = 2rS

при v ≠ v0 время t получается бесконечным. При v = v0 значение t неопределенно.

Это может быть объяснено следующим образом: плотность воздуха уменьшается по мере того, как поднимается ракета. Вес ракеты благодаря расходу топлива также уменьшается. Здесь возможны три случая.

1. Если voc = 2rS, то вес ракеты и плотность воздуха уменьшаются с одинаковой скоростью. vo определяется отношением поперечной нагрузки к плотности воздуха [ср. формулу (31)]. Это отношение остается в нашем случае постоянным, а тем самым и величина оптимальной скорости остается постоянной.

2. Если voc < 2rS, то время t будет положительным лишь при v < vo,

В первом случае ракета не может подняться выше земной атмосферы, так как при β = 0 масса ракеты тоже равна нулю. Во втором случае ракета тем более не сможет вылететь из земной атмосферы, ибо с течением времени скорость уменьшается.

3. И только в том случае, когда voc > 2rS, могут одновременно быть положительными и v — vo, и t. В этом случае значение оптимальной скорости растет со временем. Причина того, что ракеты, построенные до сих пор, были мало эффективны, заключается в том, что специалисты незнакомы с приведенными здесь положениями, и для всех этих ракет произведение v · c было слишком мало. Ракета, которая должна подняться, в высшие слои земной атмосферы (свыше 50 км), должна иметь в длину минимум 5 м.

Идеальная оптимальная скорость полета по прямой автоматически управляемой ракеты выражается:

vx = v — vo + 2tr      (39)*

Отношение начальной и конечной масс ракеты, согласно (6), составит

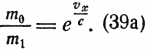
Отсюда следует

Из уравнений (38) — (39b) можно найти расход топлива для этой траектории подъема.

На фиг. 22 (а, b, с) даны для иллюстрации графики, связыйающие mo/m1, vx и β двух различных ракет. Более подробно эти зависимости будут разобраны ниже.

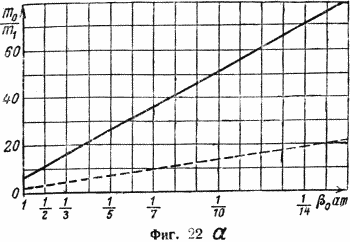
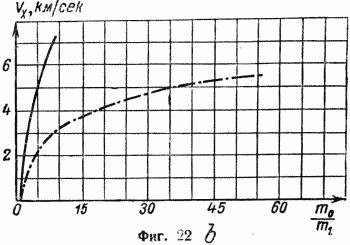
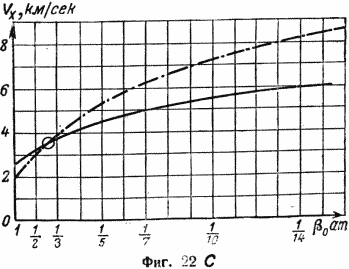
Согласно гл. IV, отношение mo/m1 не может расти безгранично. Для ракет, двигатели которых работают на нефтяных продуктах или на спирте, vx может достичь 4000 м/сек, а для ракет, работающих на водороде, 7000 м/сек. Делу можно помочь следующим образом. Когда двигатель кончает свою работу, ракета летит со скоростью, на 4—7 км/сек большей, чем до начала его работы. Если в большой ракете вместо полезной нагрузки поместить ракету в 10 раз меньшую, то в момент, когда горючее большой ракеты будет израсходовано, вся система получит скорость 4 км/сек. После этого большая ракета отделяется, а верхняя — меньшая — продолжает полет на собственном двигателе. Тогда ее собственная скорость суммируется со скоростью, которую она получила от нижней ракеты. Таким путем, пользуясь составными ракетами, можно достичь высоких конечных скоростей без того, чтобы загрузить ракету горючим, весом в 16 или даже 1000 раз большим веса самой конструкции ракеты. В рассматриваемом случае можно говорить об идеальном значении соотношения масс; это такое отношение масс, какое должна бы иметь одна ракета, чтобы достичь идеальной скорости, которой достигнет составная.

Мы находим это следующим путем.

Из уравнений (6) и (39) получим*:

Если ракета состоит из нескольких ракет (фиг. 23) и нижние после израсходования горючего отбрасываются, то предельные скорости складываются. Обозначив массы отдельных ракет через М, Ψ, μ, предельные скорости можно получить из

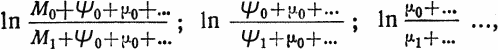
а полное приращение скорости получится, если в (40) вместо mo/m1 подставить

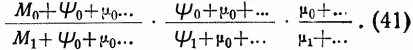
Действительно, согласно (40),

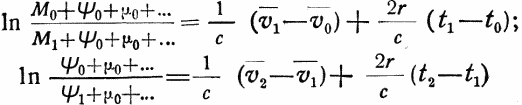
и

При сложении этих равенств получим:

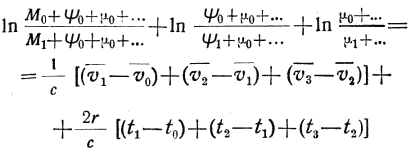
или

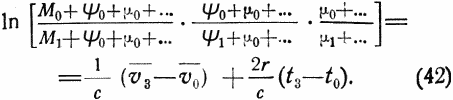
Для того чтобы одна ракета достигла такой скорости, согласно (40) должно быть:

Сравнение (42) и (43) показывает, что отношение mo/m1 должбыть равно произведению последовательных отношений масс составной ракеты.

Из С40) следует:

Это значит, что разность v1 — vo будет тем большей, чем больше с или mo/m1 или чем меньше t1 — to.

Скорость с ограничена так же, как и отношение масс, которое в одной ракете не может выйти за пределы Vσ [см. (19)]. Однако произведение отношений масс, а тем самым также и v1 — vo может иметь любое значение.

Даже в том случае, когда скорость v не соблюдается, составная ракета имеет преимущества, ибо в полете участвует меньше мертвого груза. Естественно, что и здесь величина v1/c может стать сколь угодно большой. Эти соображения действительны для идеальной скорости vx и, следовательно, для любого способа подъема ракеты.

Необходимо, однако, иметь в виду, что

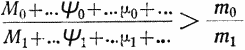
а уже последнее выражение растет относительно

по экспоненциальному закону. Если оптимальная скорость не соблюдается, то естественно, что расход массы становится ^ще большим, и мы приходим к совершенно невозможным величинам. Таким образом все же имеется предел для vv В составных конструкциях требуется, чтобы каждая ракета была больше всех остальных, находящихся в ней, так как иначе вспомогательные устройства, которые требуются для составных ракет, бУДУт слишком много весить. В моделях В и Е, например, каждая ракета должна иметь свой двигательный агрегат и др.

Совершенно аналогично должно сказываться отделение пустых топливных резервуаров в модели С. Здесь М обозначает ощую массу ракеты со всеми заполненными резервуарами, M1 - массу ракеты с опорожненным первым резервуаром, Ψ0 — массу ракеты без первого резервуара, Ψ1 - массу ракеты с порожненным вторым резервуаром и т.д. Как уже было указано, модель С является по ряду соображений идеальной для регистрирующих ракет, но для полета с людьми она не годится. Здесь имеется только один двигательный агрегат, который обеспечивает ракете постоянную тягу, и поэтому по мере уменьшения массы ускорение, естественно, все время возрастает. Если же ракета предназначается для полета с людьми, ускорение должно быть по возможности постоянным.

В качестве ракеты дальнего действия она также не годится, ибо может подниматься только вертикально вверх

Ускорение составит, согласно уравнению (37),

Идеальное ускорение bх, т.е. то ускорение, которое ракета получит при сгорании такого же количества горючего в безвоздушном и свободном от действия силы тяжести пространстве, будет равно

Сила тяги при этом будет

P = mbx = mb + 2rm       (46)

При расчетах нас часто интересует не масса сама по себе, а ее отношение к другим величинам. Действительно, скорость v зависит не от массы, а от формы ракеты и нагрузки на поперечное ее сечение, и поэтому лучше пользоваться для расчетов отношением

Отношение P/mo дает ускорение, которое сообщается начальноной массе тягой, нужной для получения оптимальной скорости. Правая часть выражения (46а) зависит не от абсолютной массы, а, как и отношение m/mo только от скорости v. Кроме того, это выражение дает меру для оценки изменения тяги, так как

и, наконец, оно показывает, что изменения давления в камере сгорания в результате изменения тяги связаны только с величинами v и с, но не с абсолютными величинами ракеты.

Следует считать удачным совпадением, что в ракетах с бензином или спиртом в качестве горючего требуемое ускорение растет примерно в такой же степени, в какой уменьшается масса. Поэтому при полете с оптимальной скоростью реактив ная сила Р остается приблизительно постоянной во все время рабсилу двигателя, особенно если ракете не сообщают в начальныи момент оптимальную скорость, а она разгоняется используя собственную тягу. При этом вначале скоробь полета будет ниже оптимальной. Поскольку реактивная сила остается примерно одинаковой, двигатели смогут развивать максимальную мощность в течение всего времени работы.

Пройденный путь определяется достаточно просто

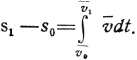
Интегрирование можно выполнить, если в соответствии с (44} выразить dt через v и dv. Тогда

Высота, которой достигнет ракета, составит

h = (s1 - so) sin α

Это — важнейшие формулы для наклонного подъема ракеты по прямой. Если в выражениях (38) — (48) принять α = 90°, то получим формулы для вертикального полета. При этом

sin α = 1; cos α = 0; r = g; S = H,

формула (38), например, примет такой вид:

Ниже в этой главе мы будем разбирать лишь вертикальный подъем. Конечно, также хорошо можно изучить и вопросы подъема ракеты по прямой и под другими углами, но для упрощения выводов мы ограничимся углом подъема, равным 90°.

Оценим теперь допущенные нами неточности. Наиболее грубой ошибкой в наших рассуждениях является то, что Н принята в формуле (34) величиной постоянной. Действительная плотность воздуха может отличаться в два - три раза от заданной (34). Рассмотрим влияние этой ошибки в несколько схематизированном примере. Пусть требуется, чтобы v1 = 11000 м/сек.
При этом разность s1 — so будет велика и значение β1 из выражения (34) особенно неточно.

Примем H = 6300 м. Это слишком мало, и если βo принято правильно, то β1 определится неверно. Пусть в начальный момент времени to ракета уже достигла оптимальной скорости v, причем vo = 500 м/сек.

Тогда, согласно (47),

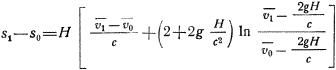
Примем, что

  ^*

Расход горючего

Если иметь в виду примечание к (38), то

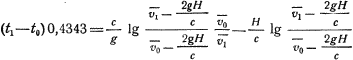
На высоте s1 — so = 62 233 м будет, согласно с принятым выше,

Но, как было сказано,

так как H > 6300 м

Если бы, например, so = 5000 м, a s1 = 67 233 м, то β1, было бы в действительности в 4 — 6 раз больше. Если же отрегулировать скорость ракеты так, чтобы во всех случаях соблюдалась скорость v, то v1 было бы достигнуто на больших высотах и немного позже. Сопротивление воздуха и сила тяжести дольше противодействовали бы подъему ракеты и она израсходовала бы больше топлива.

Примем теперь, что на высоте 67 233 м β не в 4 — 6, а в 60 раз больше подсчитанной раньше величины.

Тогда

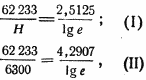
и при делении выражений (II) на (I) получим:

Но так как во все время действия реактивной силы 6300 м < Н < 10 759 м, то 40,678 < mo/m1 < 47,560.

Таким образом, если принять mo/m1 = 44, то это значение никогда не отклонится от истинного больше, чем на 7,5 % при условии правильности других данных.

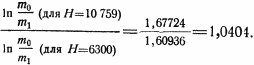
Согласно уравнению (40), ln(mo/m1) примерно пропорционален 1/c. Следовательно, такую же неточность мы получим, если значение с принято с неточностью в 2,02 %. Но с определяется с точностью в ±7 ÷ 8% и, кроме того, часто колеблется больше, чем на 4%. Таким образом допущенная неточность в определении значений β вполне допустима. При высоких скоростях движения разность v1—vo тоже пропорциональна 1/c . Таким образом в соответствии с вышесказанным, наша важнейшая задача — определение v1 из отношения mo/m1 — решается при высоких скоростях с точностью ±7 ÷ 8%, так как остальные величины, входящие в формулы, относительно мало влияют на зависимость между m и v.

Коэффициент сопротивления γ с терпимой точностью можно определить из результатов измерений, проведенных при стрельбе артиллерийскими снарядами со скоростями до v = 1000 м/сек. То, что при больших скоростях γ постоянно, является, собственно говоря, лишь гипотезой, которая, однако, подтверждается как теоретическими выкладками, так и измерениями сопротивления движущихся в воде тел. Но если бы при высоких скоростях γ и изменилось в два - три раза, то это не оказало бы влияния на эффективность ракеты. Мы показали выше, что изменение сопротивления воздуха в 60 раз лишь незначительно влияют на результаты подсчета. Еще слабее сказываются ошибки, возникающие вследствие того, что мы принимаем среднее постоянное значение g.

Более глубокая причина того явления, что принятие неточных значений β, γ и g для верхних слоев атмосферы лишь мало влияет на результат, заключается в том, что dt имеет порядок dv/v [см. (37)]. При росте v на первый план по сравнению с dt всегда выступает dv. В дифференциальном уравнении движения ракеты прирост

теряет тем больше свое значение, чем выше скорость v. Коэффициенты β, γ и g входят все три лишь в Q, а в уравнении (21) участвуют только в слагаемом приведенного типа.

При малых скоростях неизбежна большая ошибка, если принимать неточное значение Q. Однако здесь существенна одна деталь (по меньшей мере для наших ракет). Так как vo составляет уже около 500 м/сек, то при малой разности v1 — vvo значение разности s1 — so тоже мало. На таком малом расстоянии Н и g мало отклоняются от их средних значений и могут быть с достаточной точностью приняты за константы, и тем самым результат расчета будет более точным (если только достаточно хорошо известно с).

Из всего сказанного можно вывести основное правило применения наших формул: принимать для Н, g, γ, даже когда v велико, те значения, которые они имеют в нижних слоях атмосферы земли.

Коротко это можно выразить так: Q должно быть подсчитано верно для начала полета.

Важнейшей нашей задачей является определение из заданных значений mo и m1 величин vo и c/v1. При высоких скоростях полета v1 — vo примерно пропорционально 1/c. Так как при определении величины с ошибка составляет ±7 ÷ 8%, то величина разности v1 — vo имеет такую же точность и, кроме того, вследствие применения приближенных значений для β получается еще дополнительная неточность в 1—2%.

В целом мы можем в настоящее время определить v1 с точностью примерно до 1/10.

Очевидно, повышение наших знаний о величинах, входящих в формулы, желательно; особенно это относится к скорости истечения.

В случае, когда с в весьма малой степени зависит от величин L и v, можно внести поправки при помощи dm и ds, полученных по формулам (40) и (44). Сперва необходимо для этого выразить как-то δc/δv в функции v, затем надо определить dm/ds. Приближенно можно написать:

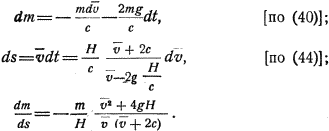
Тогда мы получим взамен (25)*

Отсюда можно определить v и по этому значению вычислить t, m, s и Р. Определение оптимальной скорости для наших аппаратов можно было бы провести и иначе, так как описанный метод рекомендуется только для случаев, когда

Затем можно (особенно легко для случая, когда с не зависит от Р) более точно выразить β и g как функции s и этим путем определить точнее и остальные величины. Формулы второго приближения дают истинные значения с точностью до 0,001. При третьем приближении рекомендуется разложить прирост v на малые промежутки и каждый из них рассчитать по формулам второго приближения. При этом для с, g, s и др. можно принять более точные средние значения и в случае необходимости получать дальнейшие приближения обычным^ численными методами. При этом следовало бы учесть, что v ≠ vg. Здесь необходимо отметить, что характеристики наших ракет подсчитаны другими методами. Но эти методы не дают таких нагляди ных формул.

Получим еще аналогичную предыдущим формулу для β. Как известно,

С учетом (47) и (48) имеем:

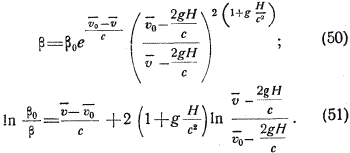
Краткие выводы

Как мы убедились, вводя соответствующие поправки в формулы первого приближения, можно получить требуемую точность. Так как поправки эти таковы, что не меняют существа вопроса, то для общего анализа мы можем применять формулы первого приближения. При этом мы можем констатировать следующее.

1. Если некоторая ракета должна пройти сквозь заданный тонкий слой воздуха и получить при этом определенный импульс, то существует определенная скорость v, при которой расход горючего будет минимальным. Но скорость v не является еще оптимальной скоростью vg. Точное значение разницы между этими величинами нас здесь не интересует.

2. Из формулы (49) видно, что если скорость истечения с зависит от тяги Р, то это сильно сказывается на v. Формулы (25) и дальнейшие действительны только для случая, когда скорость с постоянна.

3. Формула (31) может быть написана так:

Так как рассматриваемые ракеты, в особенности их головные части, подобны друг другу, то величина γ для всех ракет одинакова. Вес ракеты составляет mg, а нагрузка на поперечное сечение mg/F. Поэтому можно сказать, что оптимальная скорость для s и ds зависит лишь от отношения величины нагрузки на поперечное сечение к плотности воздуха (абсолютные величины веса, поперечного сечения, нагрузки на поперечные сечения и плотности воздуха могут при этом быть любыми).

Из (38а)

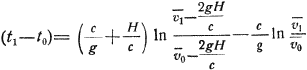
следует (так как g и Н могут считаться постоянными), что t1 - to зависит от с, vo и v1, а при заданных с и vo — только от v1. Отношение mo/m1 при заданных с и vo зависит также только от v1. Аналогичные выводы получаются для величин b, P/mo, (s1 - so), βo/β1 и т. д. [ср. (40), (44), (46а), (47), (51)].

Если составить таблицу, в которой за аргумент принять v, а перечисленные величины — за функции, то она будет верной для всех ракет, имеющих одинаковые vo и с, вне зависимости от того, как эти vo и с создаются. Это значит, что можно не учитывать значения величин веса, поперечного сечения или плотности воздуха, температуры и состава продуктов сгорания, или величин Pd/Ро, βo и т.д. в отдельности.

Еще больше: так как в дифференциальные уравнения vo, so и т.д. не входят, то при интегрировании можно исходить вместо vo из любого другого значения v, скажем, va. При этом мы получим формулы для vb — va, sb — sa, ln (ma/mb) и т.д.

Согласно правилам интегрирования,

Это означает, что таблица действительна для всех ракет и всех горючих, если только скорость ракеты равна v, а скорость истечения с.

Начальная скорость обозначается через va, конечная — через vb, тогда время (tb — ta) = (tb — to) — (ta — to). Расход горючего получится из ln (ma/mb) = ln (m0/mb) — ln (mo/ma). Высота sb — sa = (sb — so) — (sa — so) и т.д. Так как ускорения являются первыми производными скорости по времени, то расчеты не затрагивают b [см, (44)].

Для наглядности нами составлена таблица, в которой даны эти величины для с = 1400 м/сек и H = 7200 м (табл. 3)

Таблица 3
500	0,0	11,7	0,0000	1,000	31,4
600	7,3	17,0	0,0754	1,190	30,9
700	11,9	23,3	0,134	1,362	31,4
800	16,1	30,1	0,191	1,552	31,4
900	21,5	37,8	0,240	1,738	33,0
1000	21,5	40,0	0,286	1,931	34,1
1200	25,2	64,1	0,371	2,349	35,6
1400	27,7	84,3	0,448	2,803	37,0
1500	29,0	95,0	0,486	3,062	37,2
1700	31,2	117,1	0,560	3,631	37,8
2000	33,6	153,7	0,625	4,217	41,2
2200	35,0	179,5	0,735	5,434	36,7
2400	35,9	206,0	0,808	6,427	35,1
2600	36,5	234,0	0,872	7,446	34,1
3000	38,2	291,5	1,006	10,139	29,9
3400	39,3	351,0	1,138	13,74	26,9
3800	40,3	414,0	1,267	18,49	23,4
4000	40,7	447,0	1,330	21,38	21,8

Если, например, для ракеты со скоростью истечения с = 1400 м/сек, va = 800 м/сек и vb = 3000 м/сек мы хотим установить величину

то необходимо определить

и вычесть первый из второго. Получим

Время составит 38,2 — 16,1 = 22,1 сек. и т.д. Как уже было упомянуто, необходимо соблюдать условие

Выше мы установили, что vo должно быть возможно большим. В частности, если принять коэффициент сопротивления γ за константу, то при полете со скоростью v мы приходили к требованию

vc > 2rS

или, соответственно,

vc > 2gH

Здесь нелишне сделать ссылку на то, что v ≠ vg. Разница при столь низких скоростях уже значительна и ракета теоретически может как раз только выйти из земной атмосферы, если voc = 2gH, правда, при совсем фантастическом расходе топлива. Если же скорость ниже этих значений на 40 — 50 м/сек, то вылет ракеты из земной атмосферы становится вообще невозможным.

В области скоростей 330 — 460 м/сек скорость v, строго говоря, вообще не определена. Так как мы не стремимся к точности, то и здесь можем положить в основу расчетов тот случай, когда ракета летит со скоростью, при которой сопротивление воздуха равно силе тяжести:

И в этом случае квадрат скорости пропорционален отношению gm/F : β. Скорость v', так же как и v, прямо пропорциональна корню из отношения нагрузки на поперечное сечение к плотности воздуха. При этом, однако, скорость v' растет выше 460 м/сек еще медленнее, чем v, так как вследствие значительных замедлений (b' = b + 2g; 2g принимается постоянной, а b относительно мало) масса, а тем самым и нагрузка на поперечное сечение быстро уменьшается, в то время как плотность воздуха из-за медленного подъема вверх уменьшается очень медленно. И если начальное отношение между значениями нагрузки на поперечное сечение и плотностью воздуха достаточно мало, то-мы как раз подходим к той границе, где скорость, при которой имеет место наименьшее замедление, уже больше не повышается, а уменьшается, так как нагрузка на поперечное сечение уменьшается скорее, чем плотность воздуха.

Даже без применения высшей математики легко установить, что большая нагрузка на поперечное сечение является для ракеты преимуществом.

Необходимость высокой нагрузки на поперечное сечение не означает, конечно, что последняя может быть, как и в снарядах, увеличена добавлением металла. Хотя и в этом случае значение v повышается, но это лишь за счет других качеств ракеты. Таким образом к меньшей величине отношения масс mo/m1 прибавится еще необходимость того, чтобы ракета летела быстрее и, следовательно, боролась с увеличившимся сопротивлением воздуха.

Таким образом нагрузка на поперечное сечение должна быть возможно большей, вес же незаполненной ракеты — возможно меньшим.

Теперь мы подошли к выводу, что отношение vo к 2g (H/c) или, что то же самое, произведение абсолютных значений vo с должно быть возможно большим. Для того чтобы этого добиться, необходимо делать конструкцию тонкой и длинной, применять топлива с большим удельным весом, повысить скорость истечения и, наконец, совершать полет в менее плотной атмосфере. Последнее может быть достигнуто, если ракету перед стартом поднять вверх при помощи какого-нибудь летательного аппарата. Какой из этих методов предпочесть,— зависит от конкретных условий. В модели В, например, для нижней ракеты мы выбираем более тяжелое топливо, а для верхней — увеличиваем скорость истечения.

Хотя в действительности ни одна ракета не может достичь в полете оптимальной скорости, приведенные рассуждения все же имеют ценность, так как показывают, к чему надо стремиться и что можно получить при наилучших условиях. Кроме того, если не отходить очень далеко от соотношений, которые приводились нами, то различные отклонения от расчетных величин можно оценить и ввести соответствующие поправки. Таким образом наши формулы могут составить основу для более полной теории ракет.

Далее...