При отправлении важным фактором перерасхода ракетной скорости Л явится сопротивление атмосферы, которое, во-первых, само по себе понизит действительное ускорение J ракеты относительно центра Земли

Явление сопротивления среды и нагревания движущихся поверхностей теоретически изучены очень слабо, а экспериментального материала для скоростей, выражаемых километрами в секунду, нет или почти нет. Поэтому все, что мы можем знать заранее об указанных явлениях, это приблизительная их величина, определенная на основании упрощенных законов зависимости сопротивления и нагревания движущихся поверхностей от их формы, угла наклонения и скорости движения и от плотности, химического состава и температуры среды. О точном вычислении этих явлений сейчас не может быть и речи, так как они таковому не поддаются даже и для скоростей, при которых можно пренебрегать изменением плотности среды вблизи движущегося тела. В основание наших выкладок положим приблизительно в общем верную формулу:

где Q - сила сопротивления в кг; S - площадь поперечного сечения тела в м²; k - коэфициент пропорциональности, равный k = 0,25 по экспериментальным данным для скоростей, близких к скорости звука, при которых он имеет максимум; V₁ - скорость тела относительно воздуха в см/сек; с - коэфициент, зависящий от формы тела и равный единице для нормально поставленной плоскости, и Δ = ρ_h/ρ₀ - отношение плотности атмосферы в точке нахождения ракеты в данный момент к плотности ее на уровне моря.

Так как на протяжении всей настоящей работы нам оказалось удобнее оперировать с ускорениями, нежели с вызывающими их силами, то и в данном случае мы перейдем от сопротивления атмосферы к вызываемому им замедлению движения ракеты, которое мы обозначим через j_ρ. Выразив все величины в абсолютных единицах, подставив k = 0,25 и введя вместо S поперечную нагрузку ракеты Р, мы из формулы (15) получим:

где

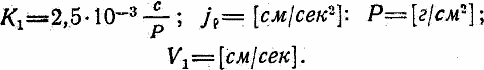
Примечание. В нашем случае, пренебрегая ветром V1 = V — U, где U — скорость вращения земной поверхности.

Как в сопротивлении воздуха, так и в нагревании движущейся поверхности можно различить две существенно различные части, являющиеся следствием различных факторов: 1) сопротивления и нагревания, обусловленных напором среды на поверхности, наклонных к их траектории, и 2) сопротивления и нагревания, обусловленных вязкостью среды, скользящей вдоль движущихся поверхностей. Первые два явления представляют собой последствия адиабатического сжатия воздуха перед обращенными вперед поверхностями тела и адиабатического расширения воздуха за обращенными назад поверхностями. Вторые два явления представляют собой последствия внутреннего трения в среде, скользящей вдоль поверхности тела. Для первых двух явлений будем употреблять обозначения сн и нн, для вторых - св и нв. Формула (16) относится специально лишь к сн, которое в общем пропорционально квадрату скорости и первой степени плотности, тогда как св в тех слоях атмосферы, где средний свободный путь молекул газов ничтожен в сравнении с размерами движущегося тела, пропорционально полуторной степени скорости движения тела и квадратному корню из плотности среды. Так как для тел, не обладающих особенно удлиненной формой*,

Основным условием каких бы то ни было влияний атмосферы является ее плотность. Если считать ускорение силы тяжести, химический состав атмосферы и ее температуру одинаковыми на всех высотах, то плотность ее будет убывающей показательной функцией от высоты, которую мы можем довольно точно в удобной для примерных вычислений форме выразить как

Примечание. Считая температуру постоянной t = —50°, каковая и наблюдается на высотах от 10 км и выше.

Примечание редактора 1-го изд. Формулу (17) обычно пишут где h - высота в километрах над уровнем моря, а

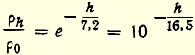
ρ₀ - плотность атмосферы на уровне моря.

Относительно состава атмосферы на больших высотах эмпирических точных данных нет, но, согласно имеющимся данным, температура и упругость воздуха при движении вверх не следуют адиабатическому закону, а именно: падают медленнее, чем следовало бы согласно этому закону. Это обстоятельство дает указание на то, что в атмосфере есть граница, выше которой не могут проникнуть перемешивающие ее восходящие и нисходящие токи воздуха. Над этой верхней границей атмосферы постоянного процентного состава, парциальные плотности всех газов при дальнейшем движении вверх должны падать уже не совместно, а для каждого газа сообразно его молекулярному весу. При этом процентное содержание, а по новейшим исследованиям — и абсолютная парциальная плотность на некоторых высотах наиболее легкого из заметных компонентов атмосферы — гелия должны повышаться почти вдвое на каждые 5 км высоты. Этот фактор при отправлении для нас благоприятен, если совершать отлет при помощи крыльев, и неблагоприятен, если крыльями продолжительно пользоваться не будем. В первом случае эта плотность дала бы опору для крыльев (вопрос же о перегреве поверхностей может стоять остро лишь в отношении азото-кислородной атмосферы, о чем будет ниже), а во втором дала бы лишь лишнее сопротивление движению ракеты, уже развившей значительную скорость. Сопротивление это, впрочем, не может быть сравнимо по величине с сопротивлением нижних плотных азото-кислородных слоев атмосферы.

Для того чтобы составить себе общее представление о ходе изменения j_ρ при отправлении, положим:

Отношение ρ_h/ρ₀ = Δ нам дано в формуле (17). Подставив из предыдущей формулы выражение для V₁², и из формулы (17) значение Δ в формулу (16), получим:

	= (по подстановке К1)=

где

Эта функция и будет характеризующей j_ρ по высоте над уровнем моря, если считать, что точка отправления находится на уровне моря. Графически она изображена при K₂ = 10 на фиг. 2; возрастая от 0 при h = 0, j_ρ принимает максимальные значения при 9 > h > 6 и затем убывает, становясь по своему характеру сходной с функцией 2^-h/5.

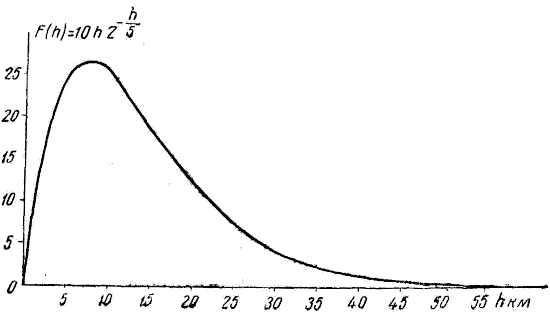
Фиг.2

Проинтегрировав F(h), мы получим величину отрицательной работы атмосферы над ракетой в дин-километрах на 1 г массы ракеты:

Заменив в F(h) множитель h через (h — h₀), и беря 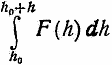что соответствовало бы перенесению точки отправления на h км вверх от уровня моря, мы получим значения в 2^h/5 раз меньше, следовательно, отрицательная работа атмосферы, а вместе с нею и Л_сн пропорциональны плотности атмосферы в точке отправления. Этот закон верен для всех траекторий, тождественных по форме и скоростям и отличающихся лишь высотою точки отправления. С этой (и только с этой) точки зрения имеет значение высота точки отправления. Для величины же W_y высота эта в возможных для нас пределах ее изменения имеет сравнительно ничтожное значение; так, например, перенесение точки отправления на 10 км вверх уменьшает W_y всего лишь приблизительно на 35 м/сек.

Чтобы найти величину Л_сн, мы должны проинтегрировать j_ρ по времени. Подставив в формулу (16) jt вместо V_l, выразив Δ через h, a h в свою очередь через t и J, как

получим:

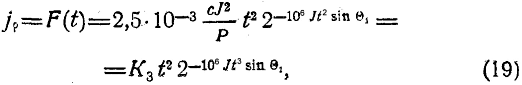
где

Примем временно произвольные данные, удобные для вычисления: J = 5000 см/сек² и Θ₁ = 90°. Тогда

где K₄ = 62 500 c/P. Функция j_ρ = F(t) при K₄ = 1/3 графически изображена на фиг. 3.

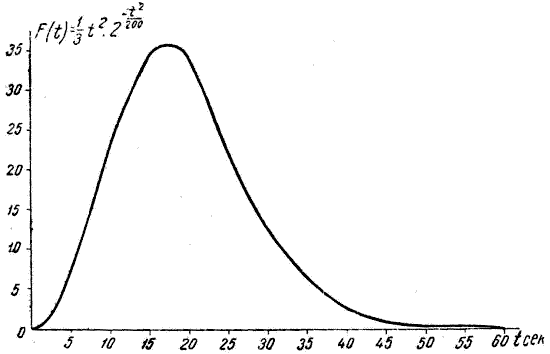
Фиг.3

Значение 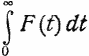по формуле (20) (или, иначе, Л_сн при J = 5000 см/сек² и при sinΘ₁ = 1) равно около 2000 K₄. Нетрудно видеть, что Л_сн должно быть пропорционально J² и sin^-3/2Θ₁. Следовательно, для всяких значений J и Θ₁ мы будем иметь:

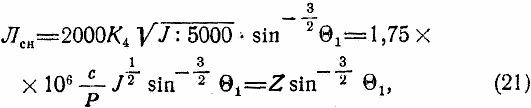
где 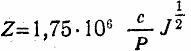= Л_сн при Θ₁ = 90°.

Наивыгоднейшим углом Θ₁ является такой угол, при котором

Примечание. Лα - перерасход ракетной скорости, зависящий от обратного действия поддерживающих поверхностей, наклоненных под углом α к траектории, мы сюда не включаем, так как он от угла Θ1 почти не зависит.

Мы положим для упрощения Θ = Θ₁ т.е. пренебрежем вращением Земли вокруг ее оси. Тогда угол Θ₁ должен отвечать уравнению:

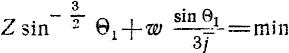
Отсюда находим

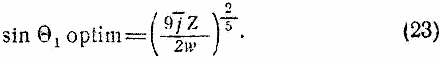
Так как в действительности мы не обязаны давать Θ₁ = const на протяжении всего J_j, но, с другой стороны, не можем и изменять его резко, особенно при больших скоростях; так как это потребовало бы большого угла β и большого Л_β, то sin Θ₁ optim по формуле (23) должен являться лишь средней величиной для участка J_j, находящегося в пределах атмосферы значительной плотности. В начале этого участка выгоднее взять Θ₁ > Θ₁optim, а затем, постепенно уменьшая, перейти на Θ₁ < Θ₁optim, поскольку этого уменьшения можно достигнуть совместным действием силы тяжести и небольшим отклонением оси ракеты от траектории (чтобы не было большого Л? нужно, чтобы β < 5—10°). Для лучшего проникновения сквозь атмосферу и достижения возможно меньшего Л_с ракета должна обладать продолговатой и заостренной формой, по направлению продольной оси которой только и может быть расположено сопло. Следовательно, на том участке Т_у, на котором Л_с может достигать значительных величин, а именно, — начиная с точки, в которой скорость ракеты V₁ достигнет значения нескольких сот м/сек, и кончая высотою около 60 км, продольная ось ракеты, а вместе с нею и ось сопла и направление реакции, во избежание излишне большого сопротивления атмосферы, должны совпадать с направлением траектории. Следовательно, нормальная к траектории слагающая реактивной силы, равная J₀M sin3 и угол β должны быть близки к нулю; при этом условии, если только на ракету не будет действовать какая-либо иная нормальная сила, траектория будет искривляться под действием нормальной слагающей силы тяжести, равной Mg cos Θ, причем радиус кривизны будет равен . При скоростях V < 2000 м/сек и при Θ, не слишком близком к 90°, это искривление траектории могло бы привести ракету к обратному падению на Землю раньше, чем она успела бы выбраться в слои атмосферы ничтожной плотности, в которых можно давать углу β произвольное значение, не создавая большого сопротивления атмосферы. Силой, противодействующей нормальной слагающей силы тяжести, может быть давление воздуха на поддерживающие поверхности, ко торыми мы должны снабдить ракету. Это должны быть поверхности из стали, покрытой тепловой изоляцией (алюминий, вероятно, будет непригоден как чересчур легкоплавкий), вытянутые вдоль корпуса ракеты и обладающие такой площадью, чтобы нагрузка их равнялась примерно 200 кг/м².

При скоростях, начиная от V₁ = 100 м/сек, достаточно будет небольшого угла атаки* (sin α < 0,1),

Примечание. Углом атаки α мы будем называть угол между поддерживающими поверхностями и траекторией ракеты.
чтобы развиваемая поддерживающими поверхностями подъемная сила уравновесила нормальную слагающую силы тяжести и тем не давала траектории ракеты искривляться вниз более, чем мы этого пожелаем. Обратное действие*

Примечание. «Обратным действием» поверхностей мы будем называть проекцию силы давления воздуха на траекторию ракеты.

***

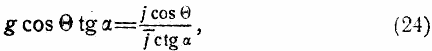
Примечание. В этой формуле, как и в формулах (13) и (14), множитель 3 в знаменателе обусловлен следующим: 1) перерасход происходит на протяжении развития ракетою лишь первых 8000 м/сек ее скорости, так как после развития этой скорости ракета становится свободным телом, и 2) по мере развития скорости от 0 до 8000 м/сек все сопротивления падают до нуля, так как они прямо связаны с кажущейся тяжестью ракеты, последняя же обращается в 0 при V = 7909 м (сек на уровне моря при горизонтальном направлении V.

Теоретическое исследование вопроса о применении крыльев для скоростей V₁ > 1000 м/сек затруднительно до соответствующих экспериментов и исследований как относительно законов сопротивления и нагревания движущих тел при больших скоростях, так и относительно состава атмосферы на высотах нескольких десятков километров. Если бы мы взяли данные современной авиации, то получили бы весьма благоприятные перспективы применения крыльев. Но, по всей вероятности, при скоростях, превышающих в несколько раз скорость звука, функция сопротивления от угла атаки приближается к ньютоновой формуле F/s = K sin²α, так что подъёмная сила поддерживающих поверхностей будет в несколько раз меньше, чем по употребительным в авиации формулам, причем сильно упадает и их авиационное качество. Вследствие уменьшения коэфицйента подъемной силы при больших скоростях ракеты при помощи крыльев ей не удалось бы до получения скорости около 7000 м/сек (при которой уже начинает сильно падать кажущаяся тяжесть) выбраться из сравнительно плотных слоев атмосферы. Следовательно, необходимо особо рассмотреть вопрос о добавочном сопротивлении вязкости атмосферы св и нагревании как лобовых частей ракеты вследствие адиабатического сжатия воздуха перед ними, так и наклонных поверхностей вследствие работы силы вязкости. Поэтому, оставляя пока открытым вопрос о возможных пределах применения полета на крыльях, будем считать, что ракета будет иметь к моменту развития скорости в V₁ = 4500 м/сек отношение j₀/g_k > 2.

В самом начале развития скорости до 100 м/сек мы должны дать β > 0, если будем иметь j > 2, а в противном случае первоначальный разгон ракеты произвести каким-либо механическим способом. В первом случае ось ракеты весьма не совпадала бы с касательной к траектории, но при малых скоростях некоторое отклонение еще не создаст слишком большого замедления сопротивлением атмосферы.

Наивыгоднейшей скоростью ракеты в данной точке ее траектории, т.е. при данных Θ и h, является такая скорость, при когорой достигается минимум Л_s для ближайшего к этой точке элемента траектории. Мы имеем, следовательно, уравнение

Л_s = Л_g + Л_c + Л_α = min(25)

причем в функциях Л_g, Л_c, Л_α нам нужно принять за переменную скорость V₁, считая Θ = const.

Примечание. Следующие выкладки, как и само понятие о наивыгоднейшей скорости, применимо лишь постольку, поскольку мы имеем Θ > α, т.е. поскольку обратное действие силы тяжести r данной точке траектории (проекция тяжести на траекторию) больше обратного действия поддерживающих поверхностей (см. примечание к стр. 55), так как при угле Θ, малом в сравнении с углом атаки α, высота нахождения ракеты в данный момент непосредственно зависит от ее скорости в данный же момент и наоборот, а угол подъема Θ определяется ходом роста скорости и, таким образом, вопрос о выборе наивыгоднейшей скорости при данных высоте и угле подъема отпадает.

Согласно формуле (10),

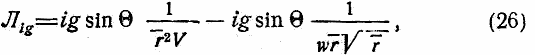
[так как α в формуле (10) будет равна 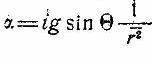]. Вопрос о наивыгоднейшей скорости имеет практическое значение лишь для участка вблизи земной поверхности в среде плотной атмосферы, поэтому мы с малой погрешностью примем r = 1. Согласно формуле (16), Л_ic = tjρ = i/V·K₁·V₁²·Δ; подставив сюда значение V₁² = V² + U² + 2VU cos Θ, получаем:

Согласно формуле (24) имеем:

Третий член формулы (27), равно как и второй член формулы (26), не заключают в себе V, следовательно, они являются в данном случае постоянными. Подставив в формулу (25) значения Л_ig, Л_ic и Л_iα, с исключением постоянных членов, получаем:

Решая это уравнение и подставляя значение Δ по формуле (17) и значение К₁ из формулы (16), получаем:

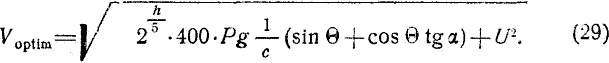
V_optim — это такое значение скорости, которое не должно быть превзойдено при полете, во всяком случае не должно быть превзойдено на значительную величину. Если бы оказалось, что при выбранных нами J и Θ на некотором участке i скорость ракеты оказалась бы значительно большей, нежели наивыгоднейшее ее значение при данных h и Θ, то следовало бы в начала этого участка несколько уменьшить J до достижения ракетой больших высот, на которых делается больше и V_optim [формула (29)]. Подставив значение Z из формулы (21) в формулу (23) и пренебрегая разницей между j₀ и J (мы это можем делать без особо большой погрешности, так как полет вообще возможен практически лишь тогда, когда между j₀ и J разница не особенно велика, т.е. когда не особенно велик Л_s), получим:

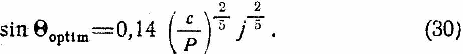
Подставив это выражение для sin Θ в формулу (21), получаем:

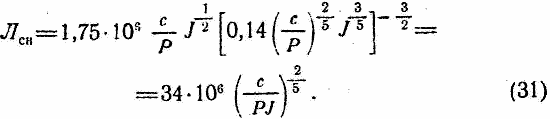
Подставив значение sin Θ из формулы (30) в формулу (14) и опять пренебрегая разницей между j₀ и J, получим:

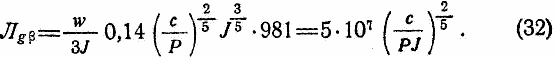
Сложив уравнения (31) и (32), мы получим Л_gβc в функций от ускорения J и при условии следования ракеты по траектории с углом подъема Θ = arc(sinΘ_opt) = const и при J = const

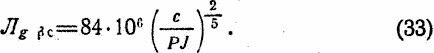
На фиг.4 дается график этой функции [формула (33)] при c/p = 1/62500 (c = 0,04; P = 2500; эти значения являются приблизительно вероятными данными). В том же графике дана и функция

[формула (24а)]

причем в последней мы пренебрегаем делителем cos Θ (который при продолжительном пользовании крыльями обязательно будет весьма близок к единице) и, как и в предыдущих формулах, считаем J = j₀.

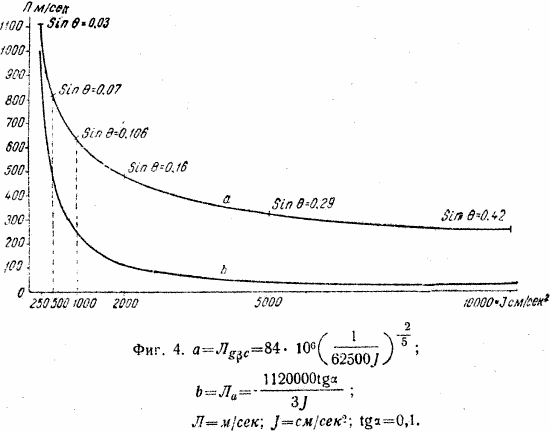
Величины Л_gβc по формуле (33) и Л_α по формуле (24а) суммировать друг с другом нельзя, так как предположения, лежащие в основе выведения этих формул, взаимно исключают друг друга. Если имеется налицо продолжительное пользование крыльями (Л_α), необходимое вследствие малого j₀ (см. стр. 56), то не может быть Θ = const; если же имеется большое j и соответственно не слишком малый Θ = const, то пользование крыльями непродолжительно и не может быть α = const. В первом случае нам следует ориентироваться более по формуле (24а), а во втором — по формуле (33); границей являются ускорения j ≈ 1.

В настоящей главе мы допустили целый ряд упрощений (при этом все в сторону увеличения сопротивлений; в частности, приравняв Θ к большему, чем он, углу Θ₁ мы увеличили расчетную потерю скорости Л_gβ, а взяв максимальное значение коэфициента К в формуле (15), мы увеличили расчетную потерю скорости Л_сн), а в формулу (33) (см. фиг. 4) ввели, хотя и более или менее вероятные, но все же произвольные данные (с = 0,04; Р = 2500) и в формуле (24) (α = 0,1) также. Принимая во внимание это, а также и то, что при отлете с углом Θ₁ < 30° (судя же по всему Θ₁ больше 30° не будет ни в коем случае), экономия W_yл от утилизации скорости вращения Земли вокруг ее оси будет составлять около 450 м/сек. Осторожным выводом из выкладок настоящей главы можно считать следующее: необходимая с учетом всех сопротивлений ракетная скорость W_yл не превзойдет 12000 м/сек, а, по всей вероятности, будет несколько меньшей.

Что касается нагревания поверхностей ракеты, то, повидимому, вопрос о нем при отправлении не будет стоять остро, что мы заключаем из следующих соображений.

Примем:
	Pv — давление в атмосферах на плоскость, движущуюся по перпендикулярному ей направлению со скоростью V м/сек; ρ — плотность атмосферы в г/см³; V — скорость в м/сек; 0,02 — коэфициент сопротивления для наибольших из исследованных скоростей;
	Р0 — упругость атмосферы в ат; Т — абсолютная температура; ρ — см. формулу (34); m — молекулярный вес (средний) газов, составляющих атмосферу.
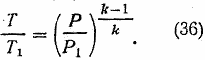	Формула адиабатического сжатия, где k = 1,41.

Рассматривая нагревание как результат адиабатического сжатия, получим для скоростей V > 700 м/сек, при которых P_v >> P₀

Примечание. В кислородно-азотной атмосфере; для других газов нижний предел применения следующей формулы пропорционален их молекулярной скорости.

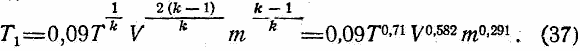
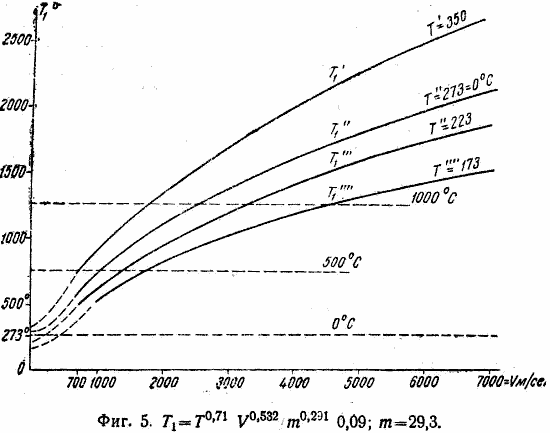
По этой формуле при m = 29,3 составлен график (фиг. 5). Формула дает температуру воздуха перед поверхностью, нормальной к траектории; такая температура будет только перед лобовыми частями ракеты — носом и передней кромкой крыльев, у поверхностей же наклонных давление и соответственно температура будут значительно ниже. Если мы лобовые части оградим каким-либо огнеупорным материалом, то остальные наружные поверхности ракеты, если они будут сделаны из стали, должны выдержать скорости до 4500 м/сек даже и без придания им особой огнеупорности. Расчеты температуры быстро движущихся тел даются нами ниже в гл. IX. Здесь применим второй способ расчета — по формуле (37), но с учетом того благоприятного обстоятельства, что мы в данном случае берем поверхности не нормальные траектории, а с небольшим углом атаки, вследствие чего сжатие воздуха перед ними, а следовательно, и их температура, будут и еще значительно ниже. К моменту приобретения ракетою скорости 4500 м/сек она будет находиться в разреженных слоях атмосферы, и, кроме того (см. стр. 56), отпадает уже надобность в крыльях.

Не менее благоприятные данные мы получим, если станем исходить из того факта, что начиненные гремучей ртутью разрывные пули самопроизвольно в воздухе не разрываются, имея начальную скорость до 700 м/сек и будучи настолько малыми, что за время полета они вполне успели бы прогреться. Температура взрывания гремучей ртути 185°Ц, так что можно полагать, что пули во всяком случае не нагреваются более, чем на 150° сверх температуры воздуха. Сделаем предположение, что абсолютная температура поверхностей движущегося тела пропорциональна некоторой степени (X) средней (квадратичной) скорости молекул газовой среды относительно этого тела. Тогда, зная, что средняя скорость молекул воздуха при 0°Ц=460 м/сек, определяем среднюю скорость тех же молекул относительно пули, летящей со скоростью 700 м/сек:

Составляем уравнение:

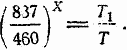
Подставляя T = 300° и T₁ < 450°, получаем X < Т. Таким образом получаем формулу:

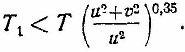
Примечание. u - средняя скорость молекул, a v — скорость движущегося тела.

По этой формуле при V = 4500 м/сек мы получим для T = 220°= — 53°Ц, T₁ < 800°Ц.

далее

назад