Изучение архива К. Э. Циолковского, хранящегося в Академии наук СССР, позволяет утверждать, что Циолковский начал систематические исследования по теории движения ракет в 1896 г. Основные формулы, относящиеся к прямолинейному движению ракет (в свободном пространстве и однородном поле силы тяжести), были получены им до 10 мая 1897 г., хотя публикацию первой части работы удалось осуществить лишь в 1903 г. [1].
Сохранился оттиск этой работы с пометками Циолковского [2]. На внутренней стороне обложки он написал: «...Все-таки я благодарен Филиппову (редактор журнала «Научное обозрение» — А. К.), ибо он один решился издать мою работу»... «Нашлась дата с формулами 10 мая 1897 г.» [1, стр. 44].
В работе 1903 г. Циолковский исследовал решение следующих задач прямолинейного движения ракет:
— движение в свободном пространстве под действием только реактивной силы;
— движение в однородном гравитационном поле Земли;
— движение с постоянным ускорением, обусловленным действием реактивной силы (масса ракеты в этом случае изменяется по показательному закону);
— безударная посадка на поверхность Земли;
— исследование скоростного коэффициента полезного действия.
Мы покажем здесь решение первой и третьей задач, сокращая несколько оригинальные расчеты и выводы Циолковского. При исследовании движения ракеты в свободном пространстве он исходит из закона сохранения количества движения, который можно написать в виде:
В соотношении (1) М — масса ракеты, dv — приращение скорости ракеты за счет отбрасывания массы dM, Vr — постоянная относительная скорость продуктов горения на срезе сопла двигателя. Из (1) следует:
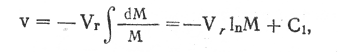
Если в начале движения М = М0, a v = 0, то C1 = VrlnM0 и, следовательно,
В работе Циолковского 1903 г. приведены значения vmax для чисел z от 0,1 до 193 (и z = ∞), причем предполагается, что компонентами топлива являются жидкий водород и жидкий кислород, a Vr = 5700 м/сек. Циолковский оговаривает, что столь высокое значение Vr получено в предположении полного превращения химической энергии реакции в кинетическую энергию частиц струи (потери не учитываются).
Приведем решение задачи о прямолинейном движении ракеты в однородном гравитационном поле Земли в предположении, что ![]()
Уравнение движения ракеты можно написать в виде:
| или | 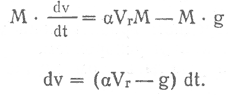 | (5) |
Полагая, что v = 0 при t = 0, из (5) интегрированием находим:
Если время горения задано (t = t2), то из (6) имеем:
Рассмотрим ту же ракету, но движущуюся в свободном пространстве в течение t2 секунд. Тогда
Исключая из (7) и (8) время t2, находим:
Формулы (9) и (10) совпадают с формулой (34), приводимой Циолковским [3. стр. 95].
Циолковский правильно указывает, что «...если р бесконечно велико, или взрыв моментален, то скорость v2 ракеты в среде тяжести та же, что к в среде без тяжести» [1, стр. 96], т. е. если р→∞, то
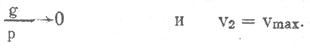
Решение основных задач ракетодинамики, «научный расчет;», как говорил Циолковский, является главным в творчестве Константина Эдуардовича. Но в его статьях, посвященных теории реактивного движения, обсуждаются и чисто практические вопросы ракетостроения, касающиеся особенностей и реального воплощения отдельных агрегатов и конструкции ракеты в целом. Так, например:
— Для охлаждения стенок реактивного двигателя Циолковский в работе 1903 г. предлагает использовать компоненты топлива. Стенки камеры и сопла двигателя он рекомендует делать двухслойными и продавливать между ними один из жидких компонентов топлива. Протекающее вещество охлаждает горячую стенку работающего двигателя. Чтобы отбор тепла был более эффективным, необходимо внутренние поверхности камеры и сопла делать из материалов с повышенной теплопроводностью. Такое принудительное охлаждение горячей стенки двигателя позволяет обеспечить длительную работу ракетных двигателей и широко применяется в современной практике ракетного двигателестроения.
— Циолковский в работе 1903 г. дает следующее описание ракеты. «Представим себе такой снаряд: металлическая продолговатая камера (формы наименьшего сопротивления), снабженная светом, кислородом, поглотителями углекислоты, миазмов и других животных выделений, предназначена не только для хранения различных физических прнборор, но и управляющего камерой разумного существа. ...Камера имеет большой запас веществ, которые при своем смешении тотчас же образуют взрывчатую массу. Вещества эти, правильно и довольно равномерно взрываясь в определенном для того месте, текут в виде горячих газов по расширяющимся к концу трубам, вроде рупора или духового музыкального инструмента... Понятно, что такой снаряд, как и ракета, при известных условиях будет подниматься в высоту» [3, стр. 81].
— Для выдерживания прямолинейного и поступательного движения ракеты Циолковский рекомендовал «...поворачивание конца раструба... », т. к. это, по мнению ученого, может служить средством сохранения определенного направления снаряда [3, стр. 83]. В работе 1911 г., излагая кратко содержание своей статьи 1903 г., Циолковский писал: «Простейшим способом управления направлением ракеты служит поворачивание конца раструба или руля перед ним» [4, стр. 113]. Отметим, что и газовые рули, помещаемые в струю истекающих из сопла горячихгазов, и покачивание всего двигателя широко применются в современном ракетостроении,
— Циолковский дает формулу, позволяющую определить запас топлива, необходимый для приобретения ракетой скорости и для «уничтожения ее», т. е. решает вопрос о мягкой безударной посадке на планету без атмосферы. Он пишет: «...Скорость ее (ракеты — А. К.) возрастает в желаемой прогрессии и в желаемом направлении; она может быть постоянной и может равномерно уменьшаться, что даст возможность безопасного спуска на планету (подчеркнуто Циолковским — А. К.). Все дело в хорошем регуляторе взрывания» [3, стр. 84].
— В работе 1903 г. Циолковский неоднократно подчеркивает, что предлагаемая им топливная пара (жидкий кислород + жидкий водород) — одна из наиболее эффективных. Он пишет: «...вообразим ряд точек, абсциссы которых выражают сумму (или произведение) атомных весов соединяющихся простых тел, а ординаты соответствующую энергию химического соединения, то, проводя через точки ...плавную кривую, увидим непрерывное уменьшение ординат по мере увеличения абсцисс, чем и доказывается наш взгляд» [3, стр. 90].
Поражает в высказываниях Циолковского широта и глубина понимания труднейших проблем ракетной техники. Заметим, что он не получил систематического образования и был «самоучкой чистой крови».
Иван Всеволодович Мещерский в годы создания основ динамики точки переменной массы был магистром Петербургского университета, учеником известного механика, профессора университета Д. К. Бобылева (1842—1918). Для дореволюционной Петербургской школы механиков и специалистов по прикладной математике руководящим принципом являлись слова А. М. Ляпунова (1857—1918) — математика и механика с мировым именем, — который указывал, что как только задача механики или физики поставлена математически совершенно строго, то «...эта задача становится тогда проблемой чистого анализа и должна быть решаема как таковая» [5, стр. 3].
Работа Мещерского «Динамика точки переменной массы» [6], являвшаяся его магистерской диссертацией, безупречна с математической стороны, и автор пишет так, что «словам тесно, а мыслям просторно».
В диссертации 7 глав, и по существу этим исследованием Мещерского были заложены основы нового раздела теоретической механики. В главе II Мещерским получены дифференциальные уравнения движения точки переменной массы и проанализированы главные следствия при учете различных сил и условий. Глава III посвящена изучению прямолинейных движений точки и в этой главе две страницы посвящены «восходящему движению ракеты» в сопротивляющейся среде. Мещерский отмечает, что восходящее движение ракеты описывается уравнением Риккати, «если сопротивление воздуха принять пропорциональным квадрату скорости». В главе VI рассматривается движение точки переменной массы в однородном поле тяготения. На стр. 121 приводится основное уравнение ракеты (формула Циолковского) в виде:
На стр. 122 кратко освещены отдельные вопросы, задачи движения точки в однородном поле силы тяжести, когда M = M0ekt, т. е. масса точки изменяется по показательному закону.
В последней, VII главе диссертации Мещерского исследуются задачи о движении точки переменной массы при действии центральной силы [6, стр. 136—157].
Среди рассмотренных задач и методов динамики точки переменной массы весьма плодотворным оказался метод отображения движения, впервые предложенный Мещерским. Идея метода состоит в следующем: находятся такие преобразования переменных реальной задачи (координат и времени) к новым переменным в некотором вспомогательном пространстве, при которых в этом новом пространстве уравнения движения точки переменной массы переходят в уравнения движения «отображенной» точки постоянной массы.
Между элементами движения вспомогательной точки во вспомогательном пространстве и элементами движения реальной точки формулами преобразования устанавливается ясно трактуемое соответствие.
Проиллюстрируем этот метод на следующей задаче: определить движение точки переменной массы притягиваемой к началу координат силой, пропорциональной массе точки и обратно пропорциональной квадрату расстояния от выбранного начала, предполагая, что масса точки увеличивается по закону
Векторное уравнение движения точки можно написать в виде
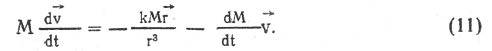
Так как в этом случае траектория точки есть плоская кривая, то, располагая оси Ох и Оу в плоскости движения и проектируя на эти оси уравнение (11), получим два скалярных уравнения:
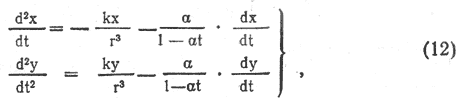
Введем новые переменные ξ, η, τ, положив:
Уравнения отображенного движения во вспомогательном пространстве (ξ, η) с новым временем τ будут иметь вид

Уравнения (13) суть уравнения движения точки постоянной массы под действием центральной силы, и интегралы этих уравнений изучены достаточно подробно. Зная решения уравнений (13), формулы преобразования координат и времени, легко найти все характеристические свойства движения точки переменной массы.
В задачах небесной механики Мещерский первый рассмотрел ряд частных законов изменения массы, полагая
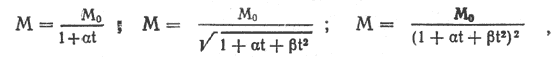
Эти предположения Мещерского, сделанные из чисто теоретических соображений, были подвергнуты обстоятельной проверке в большом числе работ крупнейших астрономов, получили хорошее подтверждение, и сейчас эти гипотезы носят в литературе по небесной механике название «законов Мещерского».
Приведем еще один из результатов Мещерского, относящийся к исследованию движения комет. «Пусть, например, рассматривается движение кометы при приближении ее к перигелию, допуская, что масса кометы уменьшается и может быть выражена некоторой функцией расстояния кометы от Солнца; тогда уравнения движения интегрируются в квадратурах, если предположить, что скорость центра инерции отделяющихся частиц или равна нулю, или направлена по одной прямой со скоростью кометы, причем отношение этих скоростей есть или величина постоянная, или некоторая функция расстояния между кометою и Солнцем» (6, стр. 139).
Мещерский первый поставил и частично исследовал задачи следующего типа: найти закон изменения массы точки, при котором она под действием заданных внешних сил описывает заданную траекторию. Эти задачи Мещерский называет обратными. Приведем здесь общее решение класса обратных задач для прямолинейных траекторий [7, 8]. Рассмотрим для определенности вертикальный подъем точки переменной массы в однородном поле силы тяжести в среде, сопротивление которой пропорционально квадрату скорости.
Уравнение движения точки будет иметь вид:
| или | 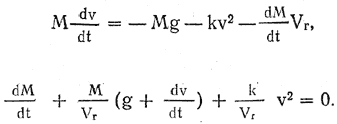 | (14) |
Уравнение (14) есть линейное неоднородное дифференциальное уравнение относительно М, и его общий интеграл можно написать в виде:
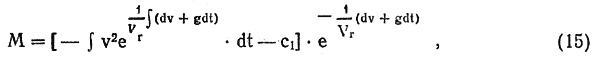
Соотношение (15) позволяет весьма просто рассчитать необходимый закон изменения массы (т. е. режим работы реактивного двигателя), если закон движения точки по прямолинейной траектории известен. Легко понять, что формулу (15) можно обобщить на переменное поле тяготения и произвольные законы сопротивления среды. Для иллюстрации приведем два простых примера на определение закона изменения массы по формуле (15) в случае когда характеристики движения точки заданы.
Пусть ускорение точки, поднимающейся вертикально вверх в однородном поле тяготения при отсутствии сил сопротивления, равно нулю. Требуется определить, как нужно изменять массу точки, чтобы обеспечить такой закон движения. Полагая в (15)
Так как М = М0 при t = 0, то окончательно будем иметь:
Таким образом, движение точки переменной массы с постоянной скоростью в однородном поле тяготения будет иметь место в том случае, когда масса точки изменяется по показательному закону (17).
Пусть мы хотим обеспечить в однородном поле тяготения равноускоренное движение точки с ускорением, равным а; из (15) легко находим, что в этом случае масса точки должна изменяться по закону:
В работе «Исследование мировых пространств реактивными приборами» (1903 г.) Циолковский дает решение двух задач, ставших особенно актуальными в связи с проблемой мягкой посадки на планету без атмосферы. Приведем сначала наше решение задачи о разгоне ракеты в свободном пространстве (от v0 = 0 до скорости v1) и торможении этой ракеты от скорости v1 до V0=0). Это решение отличается от оригинального (данного Циолковским в 1903 г.), но, как нам кажется, оно существенно проще. В самом деле, в свободном пространстве скорость v1 определяется по формуле Циолковского
Vr — относительная скорость отбрасываемых частиц.
Для торможения (от скорости v=v1, до v = 0) необходимый запас топлива, при той же Vr, будет определяться числом Циолковского z = z1. Иначе говоря, потребный запас топлива должен обеспечивать суммарную идеальную скорость v = 2v1 и, следовательно, необходимое (потребное) число Циолковского zпотр. будет определяться из условия
Легко видеть из (19), что
Из формулы (20) вытекает результат Циолковского:

Число z = zпотр. можно определить на основании формулы (21):
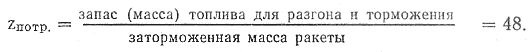
Разгон и торможение ракеты в однородном поле силы тяжести исследованы К. Э. Циолковским для случая показательного закона изменения массы. Он писал: «В простейшем случае вертикального движения процесс остановки и опускания на Землю будет такой: когда ракета под влиянием приобретенной скорости поднялась на известную высоту и остановилась, то начинается ее падение на Землю. Когда снаряд достигает той точки, в которой окончилось при поднятии действие взрывчатых веществ, он снова подвергается влиянию остатка их в том же направлении и в том же порядке. Очевидно, к концу их действия и истощения всего запаса ракета остановится в той точке у поверхности Земли, с которой было начато поднятие. Способ поднятия строго тождествен со способом опускания, вся разница лишь в том, что скорости обратны в каждой точке пути» [3, стр. 101].
Окончательная формула для zпотр. в этом случае имеет вид:
Работы И. В. Мещерского по механике тел переменной массы дважды переиздавались в СССР: в 1950 и 1952 гг. К сожалению, на Западе магистерская диссертация Мещерского «Динамика точки переменной массы» мало известна, и нам хочется этой статьей привлечь к ней внимание ученых, работающих в области истории ракетной техники.
1. К. Э. Циолковский. Исследование мировых пространств реактивными приборами. — «Научное обозрение», 1903, № 5, стр. 45—75.
2. Архив АН СССР, ф. 555, оп. 6. а, д. 39.
3. К. Э. Циолковский. Исследование мировых пространств реактивными приборами (1903 г.). — В сб.: К. Э. Циолковский. Реактивные летательные аппараты. М., 1964, стр. 77—107.
4. К. Э. Циолковский. Исследование мировых пространств реактивными приборами (1911—1912 гг.). — Там же, стр. 111—152.
5. А. М. Ляпунов. Об одной задаче Чебышева. — «Записки Имп. Академии наук», серия VIII, 1905, т. XVII, № 3.
6. И. В. Мещерский. Динамика точки переменной массы. СПб., 1897.
7. А. А. Космодемьянский. Лекции по механике тел переменной массы. «Ученые записки МГУ», вып. 154, 1951.
8. А. А. Космодемьянский. Курс теоретической механики. Ч. II. М., 1966, стр. 70—72.Ф. Д. Малина (США)