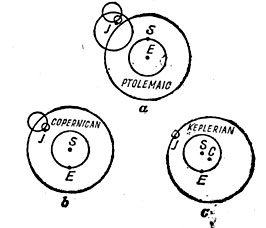
Рис. 1. а — система Птолемея; b — система Коперника; с — система Кеплера
Астродинамика является разделом небесной механики и космической навигации в их широком понимании; до запуска первого ИСЗ астродинамика рассматривала методы определения и улучшения орбит, после запуска в ее задачи были включены также проблемы управления и оптимизации.
В небесной механике различают три основных направления:
1. Аналитическая небесная механика, которая связана с проблемой существования решений для ограниченных задач небесной механики. Преимущественное распространение здесь получили методы общего характера, которые приложимы также и к другим областям механики. Но эти методы применимы для решения узкого круга проблем; например, метод потенциала и метод Гамильтона используются только в случаях консервативных и квазиконсервативных сил.
2. Физическая небесная механика, которая занимается главным образом определением физических постоянных, представляющих интерес для других областей физики, в особенности для геофизики и астрофизики.
3. Астродинамика, как мы называем третье направление небесной механики, занимается изучением физических постоянных, а также всех других факторов, влияющих на точность космической навигации, например, постоянных интегрирования, методов интегрирования, особенностей и неопределенностей. В фундаментальных исследованиях по астродинамике получили применение основные методы аналитической небесной механики, а также специальные методы, предназначенные для решения частных реальных задач. В то время как в аналитической небесной механике наблюдается стремление доводить до конечных выводов одно решение, максимально используя определенный математический аппарат, астродинамика стремится разработать все возможные решения в целях их сравнения и отбора. Аналитическая небесная механика занимается идеальными проблемами; астродинамика стремится использовать теорию для наблюдений и для установления правильного соотношения в системах реального мира, т. е. связана с изучением прецессии, нутации, аберрации, параллакса, редукцией наблюдений (как электронных, так и оптических) и теорией силовых полей, которые встречаются в реальных задачах. Общие методы и приемы (например, метод наименьших квадратов и функций Бесселя) часто вытекают из частных решений реальных проблем.
Некоторые различия между перечисленными разделами и их методами будут показаны при рассмотрении истории развития астродинамики до 1940 г.
Я начал серьезно заниматься астродинамикой и космической навигацией, когда учился на последнем курсе в колледже Вильямса. Четыре письма, полученные мной от д-ра Роберта X. Годдарда, укрепили мое решение посвятить себя изучению этих наук, а его доброта и ободряющая поддержка помогли мне даже в тот момент, когда его собственная вера в успех нашего дела ослабла. Приведу два абзаца одного из писем д-ра Годдарда от 15 июня 1932 г.:
«...Уныние привело к тому, что разработка проекта ракеты первого июля была прекращена и, как выяснилось в дальнейшем, это произошло из-за неуверенности в успехе...» «...Я не могу побороть ощущения того, что теоретическое исследование, которое Вы упоминаете, имеет преимущества над экспериментом в нынешнее время...»
Эти письма воодушевили меня, и я продолжал свои занятия под руководством Армина Отто Лейшнера, Рассела Трейси, Кроуфорда и С. Дональда Шейна в Беркли, где меня все сильнее увлекали и небесная механика, и космическая навигация.
Физическая небесная механика, можно считать, ведет свое начало с Галилея и Ньютона, когда были установлены законы действия сил и закон тяготения. Астродинамика и аналитическая небесная механика восходят по меньшей мере к Гераклиту Понтийскому, т. е. к IV веку до н. э. Открытые греками эксцентрики и эпициклы были приведены в систему Аполлонием Пергским в III веке до н. э. Эта система была усовершенствована Птолемеем из Александрии во II веке н. э., опубликована им и стала известна как система Птолемея. Принято считать, что примерно 1500 лет спустя учение об эпициклах было опровергнуто Иоганном Кеплером, однако это понятие встречается в астродинамике вплоть до нашего времени и проникло в другие области науки в виде рядов Фурье!
Взгляд в прошлое — ценный прием в истории науки, он показывает, с одной стороны, каково было восприятие и понимание идеи в свое время, а с другой — ее четкость и жизнеспособность. Историк науки, вероятно, подчеркнет первое; естествоиспытатель же, естественно, более интересуется вторым.
Мою ретроспективную теорию я излагал на протяжении более чем 20 последних лет студентам, а они делились этими знаниями с другими, однако значительная часть моих лекций осталась неопубликованной — если говорить об обычном способе печати (исключение составляют препринты моей работы «Астродинамика» [1]). В этой работе высказана мысль о том, что история была несправедлива к учению об эпициклах и даже к Николаю Копернику. (Некоторые историки заходят так далеко, что утверждают, будто бы система Коперника почти так же громоздка, как и система Птолемея, и что подлинным творцом современной гелиоцентрической теории является Кеплер).
Взгляд в прошлое позволяет увидеть, что в движении планет существует три типа отклонений от идеально кругового, с чем столкнулись уже греки и их последователи, и что требовало объяснения с помощью таких «систем», как системы Птолемея или Коперника:
1. Годовое или коперниканское отклонение, обусловленное движением Земли вокруг Солнца.
2. Эллиптическое или кеплеровское отклонение, объясняемое для ограниченной задачи двух тел, открытием того, что относительная орбита двух тел есть эллипс или другое коническое сечение.
3. Пертурбационные или ньютоновы отклонения, обусловленные взаимным притяжением планет и их спутников.
Система Птолемея объясняла все эти отклонения геоцентрическими деферентами, вызванными нагромождением эпициклов (см. рис. 1, на котором наибольший эпицикл соответствует годовому отклонению, второй эпицикл — эллиптическому отклонению, а самый меньший — пертурбативному).
Аристарх Самосский, а затем и Коперник исключили отклонения первого типа, переместив центр системы с Земли на Солнце, однако оставшиеся отклонения в системе Коперника по-прежнему нужно было объяснять эпициклами. Именно это и привело современников к утверждениям, что система Коперника «почти так же сложна, как и система Птолемея». Однако, обратив взгляд в прошлое, можно понять, что исключение пяти годовых эпициклов планет (по одному эпициклу для каждой из пяти известных в то время планет) привело к существенному упрощению механики системы; следовательно, широкое признание Коперника было вполне заслуженным.

Кеплер использовал для объяснения отклонений второго типа открытые им законы движения планет. Именно этот факт отождествляют с отрицанием роли эпицикла как элемента при построении системы. Однако следовало бы признать, что в системе Кеплера оставались все еще не объясненные пертурбационные отклонения. Особенно заметны эти возмущения в движении Луны вокруг Земли. Во времена Кеплера точность наблюдения была достаточно высокой и позволила выявить также взаимные возмущения Юпитера и Сатурна. Когда установленный Ньютоном закон всемирного тяготения дал возможность объяснить эти возмущения средствами механики, эпициклы, выдержавшие «атаку» Кеплера, вошли в механику Ньютона. Теория эпициклов получила дальнейшее развитие и даже объясняла эллиптические отклонения, что дало преимущество системе Коперника перед кеплеровской системой. Это развитие в известном смысле можно охарактеризовать как переход от практической астродинамики к математической теории.
Можно, кроме того, отметить, что ряды Фурье с аргументами, кратными одному углу, менее гибки, чем первоначальная «астродинамическая» концепция эпициклов, в которой использовались несоизмеримые аргументы: например, представление о геоцентрическом движении Венеры, в предположении, что и Венера и Земля движутся по круговым гелиоцентрическим орбитам. Концепция Птолемея предусматривает только один эпицикл; ряды Фурье требуют рассмотрения теоретически бесконечного числа членов или эпициклов. В современной теории возмущений, по существу, берется первоначальная концепция эпициклов в сочетании с некоторыми рядами Фурье, в которых аргументы выражены в разных угловых переменных.
Последние исследования в области геоцентрического параллакса показывают, что для астродинамики важное значение имеют физически реальные системы отсчета и обработка данных наблюдений, в противоположность аналитической небесной механике, в которой система отсчета идеализирована и данные наблюдения принимаются в расчет только теоретически.
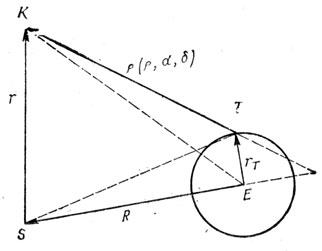
На рис. 2 показано влияние геоцентрического параллакса на наблюдения. Положение Солнца обозначено буквой S, а наблюдаемого объекта — символом кометы К; Е — центр Земли; Т — местоположение наблюдателя (от греческого слова topos — место и прилагательного «топоцентрическое»). Положение движущегося объекта К определяется вектором r (т. е. отрезком S). Положение Солнца относительно центра Земли определяется обычно «солнечными координатами», приводимыми в астрономических календарях, т. е. вектором R (на рисунке — отрезком ES). Геоцентрическое положение наблюдателя определяется вектором rT(ЕТ). Наконец, топоцентрическое положение кометы определяется вектором ς, который представляет топоцентрическоё расстояние (нынешняя «дальность») ς, прямое восхождение α и склонение δ.
В классических расчетах топоцентрические прямые восхождения и склонения корректируются на геоцентрический параллакс так, что наблюдения якобы сделаны из центра Земли; таким образом, получается треугольник ESK. При решении некоторых проблем подобная операция еще может быть оправдана, но в предварительных расчетах орбиты, основанных на значениях α и δ, установленных путем наблюдений, параллакс можно вычислить только после первого приближения, в определении значения ς. Такие последовательные приближения широко практиковались при определении элементов орбиты еще задолго до этого случая! Проводились примитивные опыты с «фиктивной точкой», которая показана на рис. 2 как пересечение прямых КТ и ES. Когда Гиббс заинтересовался проблемой определения орбит (1899) [2], главным образом в связи с его работами по векторному анализу, он был, к счастью, не знаком с практической астрономией. Поэтому он принял решение прежде всего откорректировать солнечные координаты или вектор R, проведенный из центра Земли к наблюдателю, путем вычитания известного вектора rm. Тем самым треугольник ESK был заменен треугольником KTS. Как видно из литературы, эта мысль ранее приходила на ум Чаллису (1848) [3] и, возможно, Леверье (1855) [4], но она не получила развития. В сущности астрономы не спешили использовать найденное Гиббсом простое решение в проблеме параллакса, пока не появились работы Бауэра (1922, 1932) [5], Мертона (1925) [6], Расмусена (1951) [7] и др.
Мой вклад в решение этой проблемы связан с моей работой над диссертацией [8] в 1935-1936 гг., а также с математической интерпретацией работы Пуанкаре (1906) [9].
Пуанкаре предложил второе приближение для расчета орбит по методу Лапласа. В методе Лапласа три наблюдения величин α и δ численно дифференцируются для получения скорости и ускорения угловых координат (рис. 3). Однако численное дифференцирование в
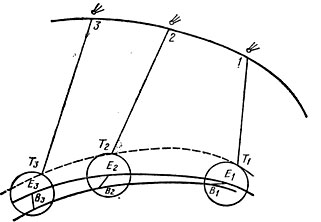
Применение в астродинамике линейных методов — один из спорных вопросов в этой области, он остается все еще не разрешенным на протяжении почти трех десятилетий, истекших после 1939 г. Многие линейные методы, основанные на исследованиях, выполненных Пуанкаре, снова были введены в небесной механике, хотя самим Пуанкаре и его последователями они не были реализованы; нелинейные же решения рассматриваемых проблем, не только существовали, но и постоянно применялись. Тем не менее некоторые из этих идей стимулировали мысль, и для них может быть найдено новое применение.
В настоящее время ясно, что линейные методы можно использовать после достаточно полной разработки теории нелинейного интегрирования, особенно для определения частных производных, но применимость их в теории интегрирования сомнительна и может оказаться ошибочной или ненужной.
Основное уравнение геометрии, используемое для сопоставления данных наблюдений и теории, относится, конечно, к той категории, для которой применимы линейные методы; оказалось, что в период до 1940 г. Штумпф (1931 г.) [14] и я (1940 г.) [8] пробовали использовать линейные комбинации разностей. Уравнение имеет следующий вид
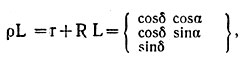
Штумпф уже предложил использование разностей двух отношений между тремя компонентами вектора L, когда я, предложив разности в самих взаимозависимых составляющих, установил эквивалентность обоих предложений. Цель их, в сущности, состояла в том, чтобы избежать последовательных тригонометрических повторных расчетов α и δ при сравнении теории с данными наблюдений.
Основная мысль Штумпфа, как я обнаружил, могла быть распространена на разности ρ либо r, или даже на «отношения треугольников», используемые при предварительных расчетах орбиты по методам Лагранжа, Гаусса и Гиббса.
При предварительном определении орбиты в теории возмущений и теории коррекции эффективно применяются различные виды разложения в ряды. Выше уже отмечалось использование рядов Фурье (или эпициклов). Степенные ряды, почти повсеместно называемые в настоящее время «f и g рядами», были получены Лагранжем (1783) [13] для уравнения типа rj=fjr0+gjŕ0, а из рядов с j=l,3 (при замене 0 значением 2) были получены ряды для упоминавшихся выше «отношений треугольников».
Гиббс (1889) со своей обычной прозорливостью перепроверил это разложение и предложил новые выражения для «отношений», составившие ценный вклад в теорию орбит [2]. Мне посчастливилось (1940 г.) распространить разработки Гиббса вплоть до получения сходных, причем даже более простых выражений для определения компонентов скорости по трем направлениям компонентов положения [8]. Благодаря этим выражениям развитый Лагранжем метод предварительного расчета орбит стал столь же эффективным, как и метод Гаусса, но более простым. Данные выражения применяются и при определении орбит, при котором используются современные электронные наблюдения параметра «дальность-скорость».
В настоящей статье не ставились задачи изложения истории формирования основ астродинамики до 1940 г., а приводятся лишь некоторые примеры, поясняющие характер самого предмета, выделившегося частично из математики. Приведенные примеры, однако, вновь доказывают, что общие принципы и идеи обычно возникают в разное время и в разных странах независимо друг от друга и что, являясь продолжением концепции прошлого, такие принципы и идеи получают применение, когда для этого наступает время.
В ближайшие десятилетия исследования должны в значительной степени строиться на основе фундаментальных работ периода до 1940 г., а также опираться на новое контрольно-измерительное оборудование, новые летательные аппараты, изыскания по предварительному определению трудно устанавливаемых физических постоянных или повышению точности взаимосвязанных констант, солнечного параллакса и других параметров, важных как для физики, так и для точной космической навигации.
1. Samuel Herrick. Astrodynamics (London, New York: Van Nostrand Reinhold, 1971), vol. 1.
2. Jоsiah Willard Gibbs. On the Determination of Elliptic Orbits from Three Complete Observations, «Memoirs of the National Academy of Science», vol. 4, 1889, pp. 81-104; Ernst Friedrich Wilhelm KHnkerfues. Theoretische Astronomie, ed., edited by Hugo Buchholz (Braunschweig: Vieweg, 1912), pp. 413-418; and The Collected Works of J. Willard Qibbs (New York: Longmans Green, 1928), vol. 2, pt. 2, pp. 118-148.
3. James C. Challis. A Method of Calculating the Orbit of a Planet or Comet from Three Observed Places, «Memoirs of the Royal Astronomical Society», vol. 14, 1848, pp. 59-77.
4. Предположение У. Леверье относительно корреляции солнечных координат было показано Э. Бауэром, но он не смог найти ссылки на этот материал.
5. Ernest С. Bower. On Aberration and Parallax in Orbit Computation, «Astronomical Journal», vol. 34, 1922, pp. 20-30; and Some Formulas and Tables Relating to Orbit Computation and Numeric Integration. «Lick Observatory Bulletin», no. 445, vol. 16, 1932, pp. 34-45.
6. Gerald Merit on. A Modification of Gauss's Method for the Determination of Orbits, «Monthly Notes» (of the Royal Astronomical Society), vol. 85, 1925, pp. 693-731; ibid., vol. 86, 1926, pp. 150-151, ibid., vol. 89, 1929, pp. 451-453. См. также Russell Tracy Crawford. Determination of Orbits of Comets and Asteroids (New York: McGraw-Hill, 1930), pp. 103-135.
7. Hans Qvade Rasmusen. Tables for the Computation of Parallax Cor. rections for Comets and Planets, Publikationer og mindre Meddelelser fra Kobenhavns Observatorium, no. 155, 1951, pp. 3-7.
8. Herriск. The Laplacian and Gaussian Orbit Methods, University of California Publication, Contributions of Los Angeles Astronomical Department, vol, 1, 1940, pp. 1-56.
9. Jules Henri Poihcare. Sur la determination des orbites par la met-hode de Laplace, «Bulletin Astronomique», vol. 23, 1906, pp. 161-187.
10. Kenneth P. Williams. The Calculation of the Orbits of Asteroids and Comets (Bloomington: Principia, 1934).
11. Armin Otto Leuschner. Short Methods of Determining Orbits (Second and third papers), Publication of the Lick Observatory, University of California, vol. 7, 1913, pp. 217-376 and 455-483.
12. Carl Friedrich Gauss. Theoria motus corporum coelestium in sec-tionibus conicis solem ambientium (Hamburg, 1809).
13. Joseph Louis Lagrange (1736-1813). Sur le probleme de la determination des orbites des cometes, d'apres trois observations «Nouvelle Memoire de 1'Academy Royale des Sciences et Belles-Lettres de Berlin»; Oeuvres (Paris: Gaut-hier-Villars, 1869), vol. 4, pp. 439-532.
14. Karl Stumpff. Uber eine kurze Methode der Bahnbestimmung aus drei oder mehr Beobachtungen — «Astronomischer Nachrichten», vol. 243, 1931, pp. 317— 336, and vol. 244, 1932, pp. 433-464.