А. Барточи (Италия)

НЕКОТОРЫЕ ФОРМУЛЫ ТЕОРИИ РЕАКТИВНОГО ДВИЖЕНИЯ, ПОЛУЧЕННЫЕ В ИТАЛИИ В ТРИДЦАТЫХ ГОДАХ XX ВЕКА

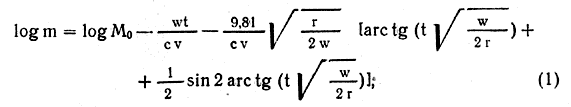
В двух статьях, опубликованных в журнале «Аэротехника» в 1933 и 1934 гг. [1], были приведены некоторые формулы и диаграммы, относящиеся к вертикальному движению летательного аппарата, имеющего постоянное ускорение, при постоянной скорости истечения газов.

Интересно отметить, что значение тормозного эффекта, создаваемого воздухом при вертикальном движении ракеты, которое подсчитывалось по формулам, помещенным в указанном выше журнале, полностью совпадает с результатами, полученными для ракеты ВМФ США «Нептун», и опубликованными в Англии в 1949 г. [2].

Вертикальное движение аппарата с постоянным ускорением

Первая группа формул относится к движению космического летательного аппарата с постоянным ускорением, что обеспечивается регулированием расхода топлива. Предполагается, что вертикальное движение ракеты осуществляется с постоянным ускорением w при данной постоянной скорости истечения газов v. Принимается, что Земля — шар радиуса r; сопротивление воздуха не учитывается.

Изменение массы m в течение времени t определяется следующей формулой:

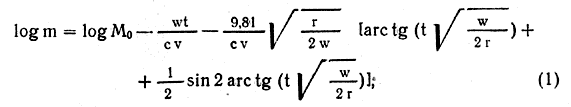
где Мо — начальное значение массы, а с = 2,30259 поправочный коэффициент при переходе от натурального логарифма к десятичному. Длина активного участка полета х и полная высота подъема h аппарата связаны следующим соотношением:
В частности для случая, когда активный участок оканчивается вне зоны притяжения Земли, это соотношение принимает вид:

На основании расчетов по приведенным выше формулам можно сделать вывод, что начальная масса, необходимая для осуществления данного полета, уменьшается с увеличением скорости истечения газов при больших значениях ускорения.

Сопротивление воздуха, которое не учитывалось в уравнении (1), определяется по следующей формуле:

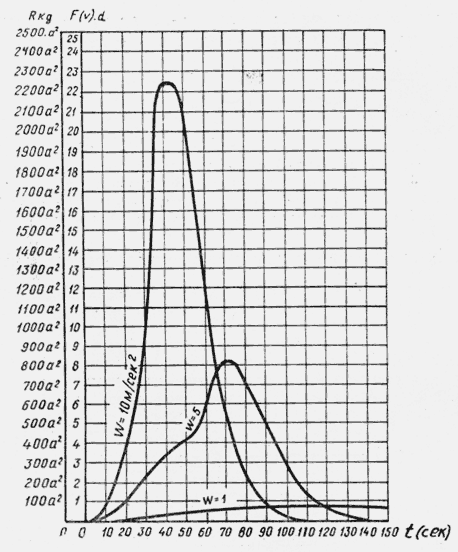
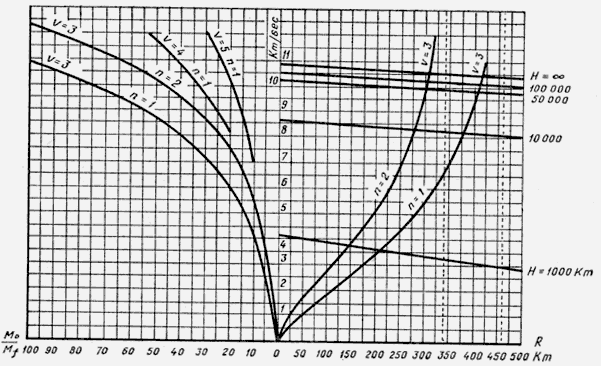
где F(V) — функция, зависящая от скорости аппарата V, d — плотность воздуха, а — диаметр поперечного сечения аппарата в метрах и i — коэффициент формы.

Принимая для функции F(V) значения, известные из баллистики, мы получаем кривые сопротивления воздуха (рис. 1).



Рис. 1. График зависимости сопротивления воздуха от времени при различных значениях ускорения

Вертикальное движение ракеты с постоянным расходом топлива

Вторая группа формул относится к полету непилотируемой ракеты; при этом рассматривается вертикальное движение ракеты с постоянным расходом и неизменной скоростью истекающих газов.

Не учитывая сопротивления воздуха и принимая ускорение силы тяжести постоянным на активном участке полета, мы получаем следующие формулы, в которых Мо — начальная масса ракеты, Mt — масса ракеты в конце активного участка, n — отношение силы тяги к начальному весу ракеты.

Время Т, соответствующее концу активного участка, определяется по формуле:

Скорость ракеты Vt в конце активного участка вычисляется по формуле:

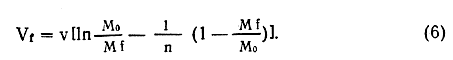
Высота h, которую достигает ракета в конце активного участка, определяется по формуле:

Начальная скорость V, необходимая для того, чтобы под действием силы инерции ракета поднялась от высоты h до высоты Н (высоте Н соответствует нулевая скорость), определяется формулой:

где r — радиус Земли. При этом предполагается, что Земля — шар. Из формул, приведенных выше, мы можем получить значение отношения масс, необходимое для достижения заданной высоты Н. В момент достижения этой высоты скорость ракеты равна нулю; до этого момента ракета движется под действием силы инерции с высоты h, на которой прекращается работа двигателя, при этом скорость ракеты равна V. По этим формулам была рассчитана более сложная номограмма (рис. 2) для вертикального подъема ракеты без учета сопротивления воздуха.



Рис. 2. Графики изменения различных параметров при вертикальном
движении ракеты (без учета сопротивления воздуха)

При учете сопротивления воздуха формулу (8) можно выразить в функции отношения где m — значение массы в данный момент времени.



Рис. 3. Графики сопротивления воздуха и ускорения ракеты
в зависимости от изменения отношения (с учетом и без учета
сопротивления воздуха)

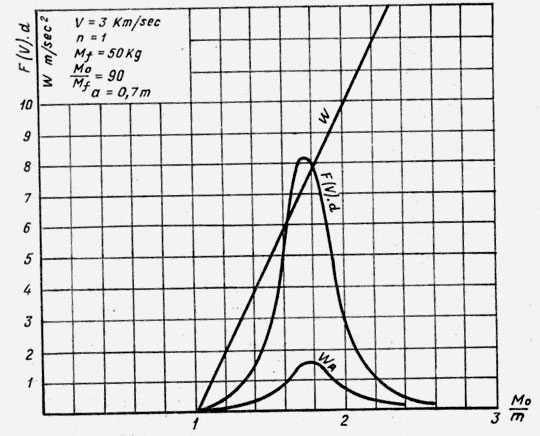
На рис. 3 приведены графики функции F(V) ·d (сопротивления воздуха), относительного отрицательного ускорения WA, а также линейной зависимости ускорения без учета атмосферы.

ЛИТЕРАТУРА И ПРИМЕЧАНИЯ

1. Aldo Bartocci, Le Escursioni in altezza col motore a reazione, «L'Aerotecnica», vol. 13, no. 12 (December 1933), pp. 1646-1666; and II Razzo, «L'Aerotecnica», vol. 14, no. 3 (March 1934), pp. 255-266.

2. В письме автору от 5 июля 1949 г. генерал Г. А. Крокко (Q. А. Сrоссо) указывал: «Я действительно имел удовольствие услышать от профессора Эулы (Eula), что Вы являетесь автором интересных статей, опубликованных в 1933, 34 и 38 годах, и был очень рад иметь письменное подтверждение этого.

Я рад сообщить Вам, что формула для скорости торможения, создаваемого воздухом при вертикальном движении ракеты, которая в настоящее время публикуется в английских журналах, для ракеты «Нептун» ВМФ США, в точности совпадает с той, которую Вы указали впервые в 1934 г.».

По всей вероятности, Крокко имел в виду работу: С. Н. Smith, M. W. Rosen, and J. M. Bridger, «Super Altitude Research Rocket Revealed by Navy», Aviation, June 1947, pp. 40-43. — Ed. *.

* Здесь и далее обозначением «Ed» отмечены примечания, сделанные редакцией американского издания трудов II симпозиума по истории астронавтики: «First Steps Toward Spase», Washington, 1974.