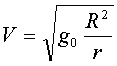
Как уже указывалось, одним из серьезных недостатков астрофизических исследований при помощи ракет является кратковременность пребывания последних в верхних слоях атмосферы. В настоящее время известен лишь один путь устранения этого недостатка — запуск искусственного спутника Земли.
Тело, вращающееся вокруг Земли по замкнутой орбите за пределами атмосферы, будет продолжать свое движение неограниченное время без затраты энергии. Теоретически вокруг небесного тела может быть бесконечно большое количество таких орбит; тело может иметь несколько естественных спутников, таких, например, как вовлеченные метеоры или Луна. После того как была высказана идея создания искусственного спутника, ученые предложили несколько проектов. Многие из них являются совершенно нереальными и свидетельствуют о незнании практики, но, с другой стороны, имеются предложения о запуске небольших ракет, оснащенных приборами, требующие серьезного рассмотрения.
В целесообразности применения искусственных спутников для исследований на больших высотах сомнений нет. С их помощью можно продолжить работу над изучением космического излучения, передачи радиосигналов в ионосфере, солнечного спектра, земного альбедо (отражения света) и, возможно, спектров планет. Прежде чем решить вопрос, относится ли запуск искусственного спутника к области фантастики или нет, необходимо рассмотреть основные теоретические положения, относящиеся к созданию искусственного спутника, а затем уже изучить все возникающие при этом инженерные проблемы.
На первый взгляд может показаться, что идея об аппарате, вечно движущемся в космическом пространстве без затраты энергии и сделанном руками человека, подрывает основы классической механики. Как известно, согласно законам механики, вечное движение невозможно. Однако ежедневное вращение небесных тел и планет вокруг Солнца и спутников вокруг планет доказывает, что такое движение осуществимо. Конечно, каждому известен тот факт, что тело, находящееся в движении, стремится продолжать это движение до тех пар, пока оно не встретит какого-либо препятствия. Строго говоря, современная теория исходит из того факта, что ничем не ограниченное движение тела, изолированного в пространстве, возможно только по прямой линии. В присутствии таких тел, как Земля или Солнце, геометрия пространства уже перестает быть простой эвклидовой геометрией; она изменяется таким образом, что траектория свободно движущегося тела становится криволинейной. В поле тяготения траектория свободного движения тела может иметь форму эллипса, параболы или гиперболы.
Следовательно, при достаточном удалении от других тел необходимо затратить энергию, чтобы заставить свободно движущееся тело следовать по криволинейной траектории, тогда как при наличии других тел требуется затрачивать энергию, чтобы заставить тело двигаться по прямой. Таким образом, если небольшое тело движется в космическом пространстве около тела с относительно большой массой, то траектория его движения будет криволинейной; при скорости меньше параболической орбита этого тела замкнется и станет эллипсом. Естественно, что тело должно будет двигаться по этой орбите, не сходя с нее. На самом же деле, если принять во внимание теорию относительности, это не совсем так, поскольку орбита не замыкается. Фактически изменение орбиты сведется к тому, что нормальный эллипс несколько исказится за счет поворота большой оси эллипса в его плоскости и соответствующего смещения положения афелия и перигелия. Такое изменение орбиты следует учитывать лишь тогда, когда речь идет о быстро движущихся телах вблизи тел с большими массами; в солнечной системе его следует принимать во внимание лишь по отношению к Меркурию — самой близкой к Солнцу планете.
Поэтому в большинстве случаев можно считать, что небесные тела двигаются по эллипсам, если не считать некоторого изменения орбит, вызываемого взаимным влиянием планет друг на друга. Некоторое отклонение вызывается также влиянием приливного трения и столкновениями с межпланетной пылью и другими частицами, которые беспорядочно разбросаны в пространстве. Движение через замедляющую среду уменьшает радиус-вектор, который определяется как линия, соединяющая движущееся тело с центром тяготения. Это сказывается в увеличении линейной скорости во всех точках орбиты с соответствующим уменьшением периода вращения. Хотя на первый взгляд это и может показаться парадоксальным, но можно доказать, что сопротивление движению тела заставляет его падать в направлении центра притяжения. В результате кинетическая энергия увеличивается за счет потенциальной энергии, а тело перемещается на орбиту, расположенную ближе к центру притяжения. Чтобы сохранить эту свою орбиту, тело должно двигаться быстрее.
Мы уже видели, что в мировом пространстве имеется множество осколков вещества в виде межпланетного газа и метеорных тел; их размеры колеблются от мельчайших частиц (меньше молекул) до тел массой в несколько тонн. Тем не менее их влиянием на планеты солнечной системы можно пренебречь, за исключением суммарного влияния за период, измеряемый в миллионах лет. Искусственные спутники, запущенные в мировое пространство, также будут подвергаться незначительному влиянию со стороны межпланетных частиц, за исключением случаев прямого столкновения космической ракеты с метеорным телом. Анализ статистических данных [1, 2] показывает, что вероятность таких случаев исключительно мала и небольшой искусственный спутник может просуществовать много лет.
Таким образом, если тело, которое уже находится в мировом пространстве за пределами экзосферы, на некотором ограниченном расстоянии от Земли привести в движение, то можно считать, что оно будет двигаться в этой среде, не оказывающей ему сопротивления, практически бесконечно долго. Можно вычислить скорость, которую необходимо сообщить телу, чтобы оно могло двигаться по круговой орбите вокруг Земли.
Простейшим случаем является движение тела по круговой орбите. Скорость, необходимую для движения по круговой орбите, можно определить, приравнивая центробежную силу силе притяжения на расстоянии, равном радиусу орбиты
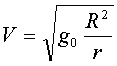
где go — ускорение силы тяжести на поверхности Земли, R — радиус Земли, r — радиус круговой орбиты. Период движения тела по такой орбите легко рассчитать по формуле
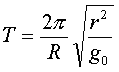
Полная энергия тела, движущегося по орбите, равна сумме потенциальной и кинетической энергий
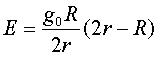
Например, тело, вращающееся на расстоянии 322 км, имело бы энергию 3,3·107 кгм/кг, тогда как тело, движущееся по орбите с 24-часовым периодом обращения, имело бы энергию 5,8·107 кгм/кг.
Можно показать, что скорость, необходимая для продолжения движения тела по круговой орбите на любой высоте в поле тяготения, равна 0,707 освобождающей скорости на этой же высоте. Естественно, что эта скорость должна быть направлена перпендикулярно радиусу-вектору. Таким образом, тело, вращающееся в пределах земной атмосферы, должно было бы двигаться со скоростью 7,9 км/сек, тогда как на расстоянии, равном расстоянию до Луны, эта скорость уменьшается до 1,03 км/сек, т. е. до скорости движения Луны по своей орбите.
Поэтому на первый взгляд может показаться, что легче разогнать ракету до круговой скорости, чем заставить ее преодолеть силу земного притяжения по параболической орбите, так как скорость движения по кругу всегда меньше 3/4 освобождающей (параболической) скорости. Но для этого необходимо поднять ракету на такую высоту, где уже не ощущается атмосфера. Простой анализ показывает, что в результате выстрела с поверхности Земли нельзя заставить тела вращаться по замкнутой орбите. Все такие тела должны двигаться по траекториям, которые пересекают поверхность Земли в двух точках: в точках взлета и падения. Для того чтобы тело стало спутником, к нему необходимо приложить движущую силу на двух различных стадиях полета.
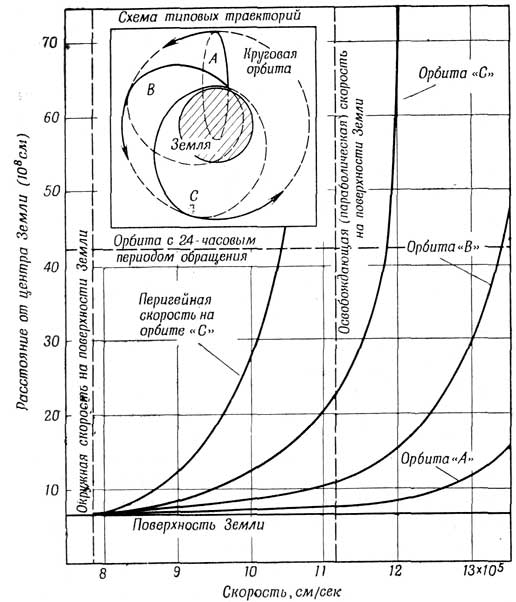 Фиг. 91. Полная скорость, которая необходима для достижения ракетой круговой орбиты, находящейся на заданном расстоянии от Земли, с использованием различных типов переносных орбит. Простейшим способом перевода ракеты на круговую орбиту является путь „С", представляющий собой эллипс, касающийся поверхности Земли и круговой орбиты. |
Возможны два предельных случая, когда ракеты выходят на круговую орбиту (фиг. 91). В первом случае орбита типа «А» предполагает вертикальный подъем по радиусу-вектору до высоты такой орбиты, после чего прилагается сила, которая изменяет направление скорости на 90° и позволяет достигнуть скорости, необходимой для движения по этой орбите. Кривая, соответствующая орбите «А», показывает, с какими напрасными потерями энергии связан этот способ. Второй предельный случай, отвечающий оптимальным условиям, связан с сообщением ракете с момента запуска горизонтального ускорения, причем она разгоняется до перигейной скорости орбиты «С», которая представляет собой эллипс, соприкасающийся с Землей в перигее и с круговой орбитой в апогее. Дальнейший прирост скорости происходит, когда ракета, совершая движение по переходной эллиптической орбите, достигает положения апогея и в этой точке переходит на круговую орбиту. Из приведенных на фиг. 91 данных видно, что прирост скорости в случае движения по орбите «С» намного меньше, чем в случае движения по орбите «А», т. е. при вертикальном подъеме. Но даже при этих оптимальных условиях для движения по круговой орбите требуется большая энергия, чем для полного выхода из поля земного тяготения по параболической орбите. Все такие круговые орбиты находятся на расстоянии больше 3,5 земных радиуса от Земли.
На фиг. 91 можно видеть, что полный прирост скорости, необходимый для перемещения ракеты на круговую орбиту (характеристической скорости), когда она близка к поверхности Земли, лишь ненамного меньше освобождающей скорости. Это вытекает из необходимости иметь два различных периода полета с работающим двигателем, что в свою очередь требует подъема двигателя и горючего в поле тяготения для использования их в апогее.
Для ближайших орбит (находящихся непосредственно за границей атмосферы) характеристическая скорость будет составлять примерно 10 км/сек; для сравнения следует напомнить, что современная ракета, как например двухступенчатая ракета «Бампер Вак», развивает скорость 2,5 км/сек. Ниже будет показано, что практически вполне возможно получить необходимое увеличение скорости после окончания работы двигателя и таким образом заставить тело двигаться по нужной орбите. Такие искусственно созданные луны будут иметь возмущенные орбиты, аналогичные любому другому небесному телу. Если рассматривать эти спутники с практической стороны, то следует выяснить, будут ли их орбиты стабильны или же под влиянием различных факторов они изменятся настолько, что смогут привести к разрушению искусственного спутника.
Во-первых, Солнце может вызвать такие возмущения, которые будут удалять спутник от Земли в соединении и противостоянии (сизигии — взаимные положения тел, при которых Солнце, Земля и спутник находятся на одной прямой линии) и приближать его к Земле в квадратурах (когда линия, соединяющая центры Солнца и Земли, образует прямой угол с линией центров Земли и спутника). Это явление аналогично силе, вызывающей приливы, поскольку речь идет об ускорениях, участвующих в процессе.
Возмущения могут возникнуть от экваториального вздутия Земли в тех случаях, когда орбита спутника находится недалеко от Земли. Если плоскость орбиты составляет угол с плоскостью экватора, то точки пересечения (узлы)1 будут перемещаться с востока на запад. Под влиянием Солнца узлы орбит также перемещаются с востока на запад в соответствующей плоскости, которая является промежуточной между плоскостью эклиптики и плоскостью земного экватора (фиг. 92). В случае эллиптической орбиты экваториальное вздутие также вызывает перемещение линий апсид, что приводит к изменению геоцентрической долготы перигея и апогея.
1) Узел орбиты — это точка пересечения орбиты с плоскостью эклиптики. — Прим. перев.
Луна, которая, как известно, имеет довольно большую массу и находится сравнительно близко от Земли, также вызовет значительное изменение орбиты искусственного спутника, но лишь в исключительных случаях уведет спутника с его орбиты. Если плоскость орбиты спутника
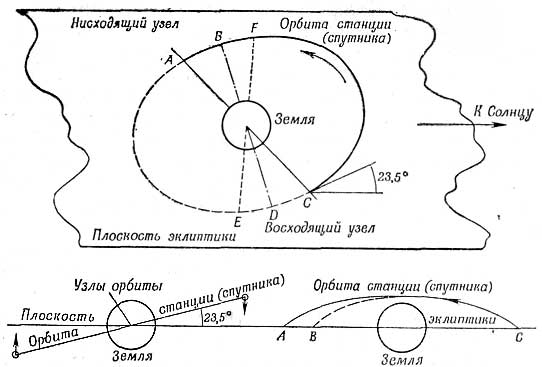 Фиг. 92. Влияние Солнца сказывается в регрессии узлов орбиты спутника. Поднимаясь над плоскостью эклиптики в точке С под влиянием Солнца, спутник вынужден вернуться в эту плоскость скорее, чем он сделал бы, не испытывая влияния Солнца. Поэтому нисходящий узел смещается из точки А в точку В. Аналогично, находясь под плоскостью эклиптики, спутник под влиянием Солнца перемещается обратно таким образом, что узлы смещаются из точки D к точке Е. |
Действие подобных разрушительных возмущений можно наблюдать на примере промежутков в кольцах Сатурна и в поясе астероидов, огромное количество которых окружает Солнце между орбитами Марса и Юпитера. Промежутки в кольцах представляют собой орбиты маленьких лун, периоды вращения которых пропорциональны периодам вращения спутников Сатурна, тогда как промежутки в поясе астероидов находятся на таких расстояниях от Солнца, что периоды вращения тел, движущихся по этим орбитам, должны быть соизмеримы с периодом вращения Юпитера.
Луна будет так же влиять на искусственный спутник, как планеты солнечной системы влияют друг на друга. Радиальные и ортогональные компоненты возмущающей силы повлияют на период вращения спутника и вызовут вращение линии апсид и смещение узлов орбиты спутника. Эти явления можно исследовать методами небесной механики, которые позволяют объяснить влияние планет солнечной системы друг на друга.
В табл. 8 приводятся различные возмущения движения спутника Земли, вызванные влиянием Луны, Солнца и Земли. На основе данных таблицы можно прийти к выводу, что при правильном выборе орбиты изменения будут не настолько велики, чтобы нарушить стабильность орбиты искусственного спутника; они только видоизменят ее форму.
Если бы по круговой орбите удалось запустить даже небольшой искусственный спутник без приборов таким образом, чтобы за ним можно было вести наблюдения с Земли, то подобный запуск оказался бы полезным не только для навигации; его можно было бы также успешно использовать для физических исследований при помощи отражения радиоволн и наблюдения за его звездной величиной. Таково первое реальное использование искусственного спутника,
Таблица 8
| Источник возмущения | Результат воздействия |
| Луна | Прямое вращение линии апсид (с запада на восток) Смещение узлов с востока на запад (регрессия) Изменение эксцентриситета орбиты Изменение периода движения по орбите |
| Солнце | Увеличение периода обращения Прямое вращение линии апсид Ускорение движения в соединении и противостоянии и замедление в квадратуре Превращение круговой орбиты в эллиптическую с большой осью, расположенной под прямым углом к радиусу-вектору, соединяющему Солнце и Землю Изменения эксцентриситета эллиптической орбиты в зависимости от положения линии апсид, а также изменения периода вращения вследствие эллиптичности орбиты Земли Неравномерность движения по всей орбите: наибольшая векториальная скорость перед соединением и наименьшая — перед противостоянием |
| Земля | На эллиптической орбите, не наклоненной к плоскости экватора, прямое движение линии апсид На наклонной эллиптической орбите прямое движение апсид и регрессия узлов На круговой орбите, наклоненной к плоскости экватора, регрессия узлов |
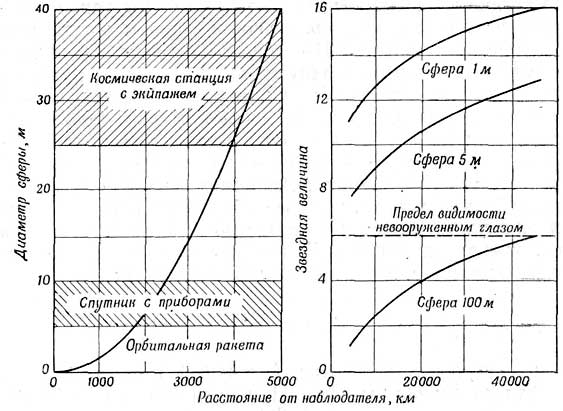 Фиг. 93. Обнаружение искусственного спутника с помощью радиолокационных и оптических установок. |
Метод оптических наблюдений также не всегда дает благоприятные результаты. Приняв альбедо спутника равным 0,4, можно определить видимую звездную величину для сфер различных радиусов. Из фиг. 93 можно также видеть, что спутника, находящегося на ближайших орбитах, невозможно увидеть невооруженным глазом, если он является шаром радиусом меньше 3-4 м. Однако спутник легко может быть обнаружен посредством телескопа с умеренной апертурой. Для будущих полетов представляет интерес тот факт, что крупную межпланетную станцию диаметром 100 м можно будет увидеть невооруженным глазом на расстоянии, равном расстоянию до устойчивой орбиты с 24-часовым периодом обращения. Судя по всему, идея запуска искусственного спутника кажется вполне реальной. Однако этот запуск связан с целым рядом проблем. Возникает вопрос, можно ли будет обойтись без атомного двигателя, без трудно выполнимых конструкций или новых горючих веществ? Предварительный анализ показывает, что для достижения требуемой характеристической скорости, необходимой для запуска спутника ни ближнюю орбиту, потребуется трехступенчатая ракета. Конечная скорость выражается в соответствии с экспоненциальным законом:
1) Это нереально, ибо при этом по мере выгорания топлива устойчивость будет теряться.
Существует большое количество различных комбинаций горючих веществ, которые теоретически могут обеспечить получение удельного импульса свыше 250 сек., но практически двигатели в основном имеют максимальный импульс около 200 сек. Некоторые смеси могли бы дать удельный импульс 300-350 сек., но такие результаты можно получить только на экспериментальных установках. К подобным смесям следует отнести фтор и гидриды бора, но такая смесь с большой энергией не требуется для простой ракеты-спутника. В табл. 9 приводятся некоторые смеси, которые уже в настоящее время могут дать требуемый импульс.
Таблица 9
| Окислитель | Горючее | Удельный импульс | Температура, °С | Импульс плотности |
| Жидкий кислород | Гидразин Аммиак | 260 250 | 2800 2750 | 272 250 |
| Анилин | 230 | 3250 | 350 | |
| Красная дымящая азотная кислота | Гидразин Анилин | 245 230 | 2800 | 310 272 |
| Перекись водорода | Гидразин | 250 | 2400 | 303 |
Горючие смеси оцениваются в зависимости от импульса плотности и удельного импульса. Естественно, что плотность следует принимать во внимание, поскольку от нее зависит относительная масса, которая может быть получена. Хотя смесь жидкого водорода и жидкого кислорода может дать высокий удельный импульс, плотность этих компонентов такова, что в результате неблагоприятного влияния ее на относительную массу получится более низкая конечная скорость (при выгорании всего топлива), чем при сгорании другой смеси — менее эффективной, но имеющей большую плотность.
В настоящее время уже нет сомнений, что удельный импульс, равный 250 сек., будет достигнут при использовании эффективных форсунок для обеспечения максимального коэффициента сгорания, совместно с испарительным охлаждением, которое дает преимущество при огромных температурах в камере сгорания. Если такие факторы, как токсичность горючих веществ, простота погрузки, производство, хранение, стоимость и пр., имели значение для ракет-снарядов, то они далеко не так важны для ракет, предназначенных для научных исследований.
Наконец, следует рассмотреть полезную нагрузку искусственного спутника. Расчеты показывают, что потребуется 1000 частей массы при взлете на одну часть полезной нагрузки при входе на орбиту. При этом предполагают, что удельный вес полезной нагрузки составляет 0,1 (на ракете «Фау-2» он равнялся 0,08, а на ракете «Викинг» — 0,17). Если вместо простой ракеты мы захотели бы иметь ракету с полезным грузом, представляющим собой телеизмерительные приборы и источники энергии весом 90 кг, то постройка такой орбитальной ракеты производилась бы по следующим расчетам:
| 1-я ступень | 2-я ступень | 3-я ступень | |
| Полезная нагрузка | 8,94 | 0,894 | 0,089 |
| Конструкция ракеты | 13,4 | 1,34 | 0,134 |
| Горючее | 67,02 | 6,70 | 0,670 |
| Всего | 89,36 | 8,934 | 0,893 |
Для ракет первой ступени необходимости в новом мощном моторе нет, поскольку четырех моторов типа «Фау-2» с общей тягой 104 т вместе с кольцом ячеистых сбрасываемых ускорителей вполне достаточно. Особых конструктивных трудностей также не встретится, а насосы, способные обеспечить подачу необходимого количества горючего, вполне доступны. Ракеты второй и третьей ступени почти не будут отличаться от орбиту. Разработка таких приборов для управляемых снарядов, которая проводится в настоящее время, значительно облегчит эту задачу.
Первые опыты, вероятно, заключались бы в определении характеристик экзосферы. Полезная нагрузка, которую нужно поместить на орбиту спутника, может состоять из расширяющейся нейлоновой или пластмассовой сферы с небольшим металлическим покрытием для обнаружения его при помощи радиолокационной установки (либо на самом шаре должен быть установлен ответчик). Орбиты таких сфер, расположенных на различных высотах, будут подвергаться изменениям в результате воздействия экзосферных газов; зная эти изменения, можно рассчитать плотность и протяженность экзосферы. Все эти вопросы необходимо изучить заранее, прежде чем будет сконструирован искусственный спутник для движения по орбите, расположенный сравнительно близко от Земли.
Одной из трудных задач является обеспечение источниками энергии спутника, оборудованного большим количеством приборов. В обычной высотной ракете источниками питания может быть занято около половины полезной нагрузки; при этом оборудование обеспечивается питанием в течение всего лишь нескольких минут. Было бы непрактично обеспечивать питание приборов от батарей или за счет энергии топлива, которое будет тратиться на вращение генератора. Правда, остается еще возможность использовать «свободную» энергию, наиболее вероятным источником которой является солнечная радиация. Рассмотренная система представляет собой «солнечный» регенератор, который преобразует энергию, излучаемую Солнцем (каждый квадратный сантиметр поверхности Солнца излучает 92 000 кал/мин). На среднем расстоянии между Землей и Солнцем (150 000 000 км) плотность этого излучения в значительной мере уменьшается, но все же известно, что 1 см2 площади, перпендикулярной к солнечным лучам, получает ~ 2 кал/мин. Эта величина называется солнечной постоянной; выше было уже показано, что точное ее определение стало возможным благодаря развитию техники ракетных исследований.
Как предполагают, специальное зеркало будет фокусировать солнечные лучи на кольцах, через которые циркулирует рабочее вещество. Если площадь зеркала равняется 1 м2, то получаемая энергия будет составлять
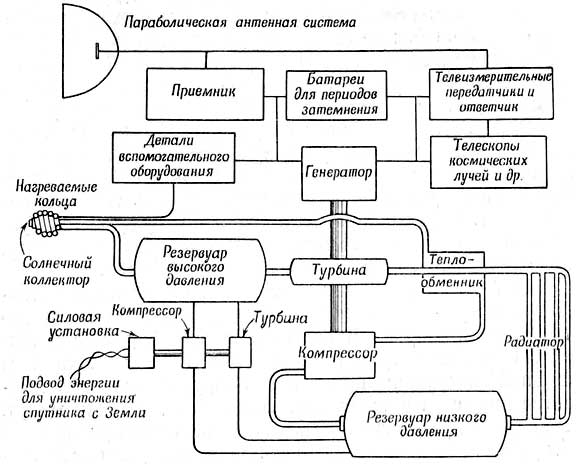 Фиг. 94. Схема силового агрегата и электросистемы для оснащенного приборами спутника. Энергия солнечной радиации используется для нагрева рабочего вещества. Последнее приводит в движение турбину, соединенную с генератором, который дает электрический ток. |
Для перекачки рабочего вещества из бака с низким давлением в части системы с высоким давлением необходим компрессор, связанный с валом турбины. Было бы довольно выгодно применить в такой системе рабочее вещество с высокой удельной теплоемкостью (обычно одноатомные газы). Однако рабочее вещество должно также обладать высокой плотностью для уменьшения габаритов аппарата, а также числа ступеней компрессора и турбины. Если спутник предназначается для продолжительного полета, при котором необходимо обеспечить отсутствие эрозии и химического разрушения, то следует употреблять преимущественно инертное рабочее вещество. Вполне возможно, что в качестве такового лучше всего использовать аргон, который имеет сравнительно высокую плотность и является инертным и одноатомным газом. Рабочим веществом могут служить также пары ртути, но высокая точка замерзания (234,1°К по сравнению с 84°К для аргона) ограничивает цикл при более низких температурах. Мощность, необходимая для телеметрирования на Землю сведений с космического корабля, движущегося у границ атмосферы, будет равняться примерно 100 вт; такую мощность вполне можно получить при помощи подобной установки.
Искусственные спутники, оснащенные приборами, в первую очередь будут использоваться для расширения программы исследований, проводившихся при помощи высотных ракет. В космическом пространстве в течение относительно большого периода времени могли бы работать телескопы космических лучей, счетчики и другие приборы; представилась бы возможность исследовать спектры Солнца, Луны и Земли, а также магнитное поле Земли, особенно во время хромосферных вспышек на Солнце. Искусственный спутник будет служить как бы своеобразной солнечной обсерваторией, при помощи которой ученые смогут получать сведения о солнечном излучении в далекой ультрафиолетовой области спектра. Это даст возможность лучше узнать природу солнечных корпускул и их связь с магнитными бурями и полярными сияниями. Благодаря запуску искусственного спутника можно будет разрешить проблему внезапного возникновения магнитных бурь и выяснить правильность предположения, высказанного Гоулдом [3], который считал, что поток солнечных корпускул создает ударную волну в межпланетном газе. Для измерений интенсивности в важнейших областях спектров других планет можно было бы запустить несколько ракет со стабильными платформами, такими какие сделаны, например, в «искателе» Солнца. Таким образом удалось бы исследовать планеты Марс и Венеру и устранить ряд неясностей относительно строения их атмосфер.
После создания искусственного спутника, когда появится некоторый опыт в управлении и в наблюдении за его приборами на расстоянии, вряд ли будут существовать непреодолимые трудности, препятствующие запуску космических кораблей в глубь межпланетного пространства. Тогда будет предпринята попытка приблизиться к другим планетам или войти в орбиту Марса или Венеры.
Поскольку все планеты солнечной системы движутся в одном направлении вокруг Солнца со скоростями, значительно превышающими скорость, которая необходима для преодоления гравитационного потенциала Солнца при подъеме или падении, известно, что траектории перехода с одной орбиты на другую представляют собой эллипсы с Солнцем в одном из фокусов. Более того, эллипсы, обеспечивающие минимальные затраты горючего на переход с одной орбиты на другую, касаются этих орбит в момент взлета и по достижении конечной цели. Они известны под названием тангенциальных переходных эллипсов [4].
Хотя планеты движутся по эллиптическим орбитам вокруг Солнца, их орбиты не находятся точно в одной и той же плоскости. Орбита Марса наклонена к эклиптике под углом 1,85°. Вследствие эллиптичности орбит расстояния от планет до Солнца и их скорости изменяются во время движения по орбите. Земля находится в перигелии приблизительно 1 января, будучи ближе всего к Солнцу зимой в северном полушарии. В этой точке она находится на 5 000 000 км ближе к Солнцу, чем в афелии. Более того, в перигелии скорость движения по орбите равняется 30,25 км/сек по сравнению со скоростью 29,26 км/сек на самой отдаленной части орбиты. Марс же, напротив, достигает перигелия в той части своей орбиты, которая совпадает с положением Земли в конце августа, при долготе 335,1°. Долгота измеряется от положения Земли в осеннем равноденствии (на радиусе-векторе, направленном к созвездию Овна). Следовательно, перигелий и афелий Марса не совпадают с перигелием и афелием Земли и, кроме того, ни тот ни другой не попадают в плоскость земной орбиты! Восходящий узел отстоит на 49,1° от положения осеннего равноденствия Земли.
 Фиг. 95. Орбиты Земли и Марса. Показано положение афелия и перигелия, а также орбитальные скорости в этих точках (расстояния даны в миллионах километров). |
Приведенные цифры дают возможность сравнить эти две орбиты и установить, когда расстояние между планетами будет минимальным или максимальным (фиг. 95). Кроме того, можно определить характер перехода с одной планеты на другую. Важные данные, относящиеся к орбитам Земли и Марса, представлены в табл. 10, а данные, относящиеся к самим планетам, в табл. 11.
Таблица 10
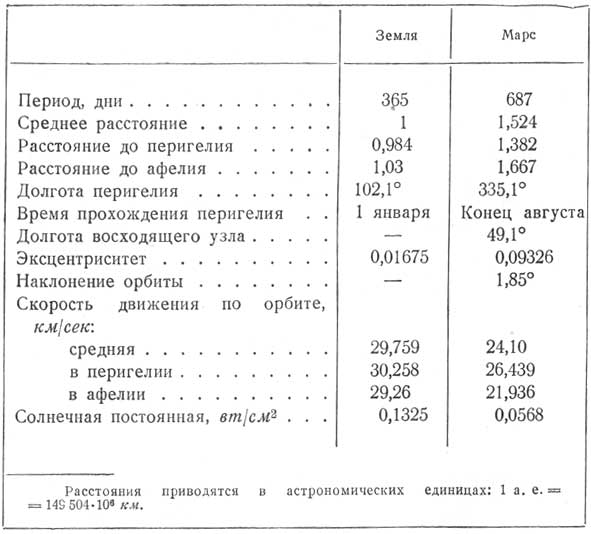
Таблица 11

Известно, что при достижении освобождающей скорости тело, преодолев силу земного притяжения, может двигаться в бесконечность (теоретически). Если тело начинает полет с более высокой (гиперболической) скоростью, то в бесконечности у него сохранится остаточная скорость. К этому необходимо стремиться при посылке космического корабля в бесконечность, но следует помнить, что практически под бесконечностью подразумевается очень большое расстояние от Земли (в отличие от математического понятия бесконечности). В действительности ракетный двигатель должен сообщить космическому кораблю такую скорость, чтобы, преодолев сопротивление силы тяжести Земли, он имел остаточную скорость. Эта скорость необходима для перехода с орбиты Земли вокруг Солнца на эллиптическую орбиту, афелий которой находится на расстоянии, равном расстоянию до Марса. Это одно из главных требований, предъявляемых к кораблю, который полетит на Марс. Если бы такой полет был совершен, то телеизмерительные установки смогли бы передать данные, полученные во время пребывания вблизи этой планеты.
Можно подсчитать, с какой скоростью, превышающей освобождающую скорость, нужно оторваться от Земли, чтобы получить необходимую остаточную скорость. На фиг. 96 показаны эти начальные скорости, которые суть не что иное, как скорости, приобретаемые ракетой после полного выгорания горючего и необходимые для покрытия рассчитанных расстояний от Солнца. Из фиг. 96 видно, что увеличение скорости даже на несколько сотых километра в секунду при полном сгорании топлива может вызвать значительные изменения конечных результатов.
При запуске ракеты с Земли возможны два крайних случая: ракету можно запустить в перигелии, когда Земля движется очень быстро, но ближе всего находится к Солнцу, или, наоборот, запуск может состояться в афелии. Результаты также показаны на фиг. 96, из которой видно, что с точки зрения расхода горючего гораздо выгоднее запускать ракету с Земли в афелии. Возникает естественный вопрос, когда лучше всего приблизиться к Марсу — в афелии или перигелии?
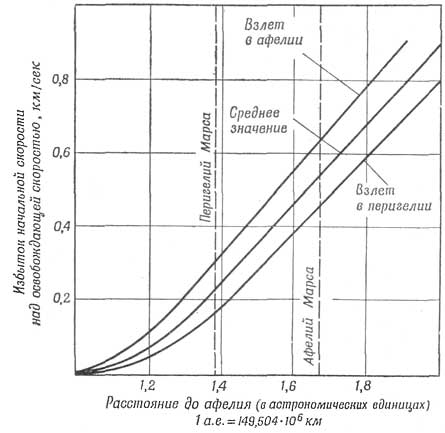 Фиг. 96. Скорости, значительно превышающие освобождающую скорость и необходимые для достижения различных расстояний от Солнца при взлете с Земли в положениях перигелия, афелия и в промежуточном положении. |
Результаты анализов [5, 6] показывают, что удобнее всего приблизиться к Марсу, когда он находится в афелии. Из общего закона [5] следует, что для перелета на любую планету, имеющую меньшую освобождающую скорость, чем освобождающая скорость на поверхности Земли, требуется большая скорость на промежуточной орбите и при переходе с орбиты Земли на эту орбиту.
Как упоминалось выше, линии апсид двух орбит не совпадают, и ракета не может быть запущена с Земли по тангенциальному промежуточному эллипсу в перигелии: она не достигнет Марса в афелии. Ракета должна покинуть Землю за 54 дня до достижения Землей перигелия, т. е. примерно 26 февраля. При приближении ракеты к Марсу со скоростью, равной освобождающей скорости, потребуется изменить скорость на 0,64 км/сек, чтобы попасть на круговую орбиту около Марса с радиусом 18 500 км и периодом вращения 21 час (фиг. 97). Установлено, что характеристическая скорость наиболее выгодной к афелию орбиты равна 14,1 км/сек.
Расчеты показали, что ракета должна иметь по крайней мере три ступени с относительной массой 4,2 и удельным импульсом 325 сек.; первая и вторая ступени должны иметь отделяющиеся конструкции. Схема такой исследовательской ракеты приведена на фиг. 98. Найдено, что на каждую единицу массы полезной нагрузки искусственного спутника, который будет двигаться по орбите Марса, потребуется 1275 единиц массы при взлете. На фиг. 98 приведен также график прироста скорости и показывается, как достигается характеристическая скорость на различных стадиях с учетом основных потерь.
Во время полета на Марс будут проводиться в основном пять видов измерений. Прежде всего, крайне важно получить точные данные о положении самого корабля, без чего другие данные потеряют всякую ценность. Местонахождение спутника по отношению к Солнцу можно определить при помощи фотоэлементов. При помощи таких же фотоэлементов можно будет обеспечивать разложение оптического изображения для получения детальной фотографии поверхности Марса. Кроме того, в задачу искусственного спутника входит измерение магнитного ноля планеты и его интенсивности, определение интенсивности космических лучей для исследования влияния гелиоцентрического поля на спектр первичных космических частиц и, наконец, измерения при помощи радиолокационных установок для получения приблизительной контурной карты планеты.
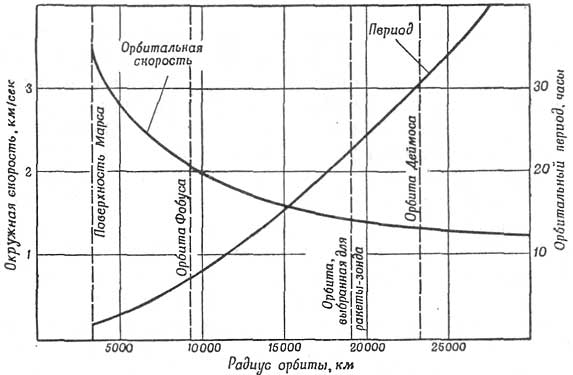 Фиг. 97. Орбитальные скорости и периоды спутников Марса. |
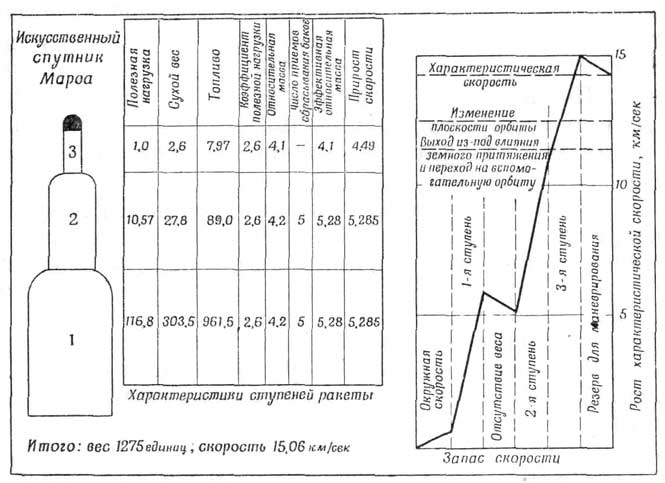 Фиг. 98. Требования, выполнение которых позволит ракете стать искусственным спутником Марса. Для каждой единицы массы полезной нагрузки требуется при взлете 1275 единиц массы. Конструкция 1-й и 2-й ступени ракеты должна обеспечивать их отделение. |
Необходимо также выяснить возможность передачи телеизмерений с Марса на Землю. Пренебрегая (на время) огромным расстоянием, отделяющим обе планеты в противостоянии и соединении, мы должны учесть, что не все противостояния одинаково благоприятны. При наиболее близких противостояниях, какие произойдут, например, в 1956, 1970 и 1985 гг., Марс будет находиться на расстоянии 56·106 км, тогда как при отдаленных противостояниях расстояние между Землей и Марсом равно 10·107км. Следовательно, при неблагоприятном противостоянии для передающей станции требуется в четыре раза больше энергии, чем при благоприятном.
Более того, расстояние, разделяющее планеты, изменяется достаточно быстро как до, так и после противостояния (фиг. 100). На фиг. 102 приводится мощность, необходимая для передачи данных на Землю для случая неблагоприятного противостояния. Эту энергию, как и на искусственном спутнике, можно получить от установки с замкнутым циклом, работающей на солнечной энергии. При этом, однако, следует учесть, что при движении по орбите Марса солнечная постоянная значительно изменяется. На фиг. 101 графически изображено изменение значений солнечной постоянной на орбите Марса в течение 6 мес. перед благоприятными и неблагоприятными противостояниями и после них. Данные, приведенные на фиг. 101 и 102, показывают ограниченность полезного времени передачи со спутника Марса. Количество необходимой для этого энергии неизвестно.
Предположим прежде всего, что применяются антенные системы, из которых наибольшая должна находиться на Земле, поскольку размеры разведывательной ракеты будут существенно лимитировать размеры ракетного оборудования. Чтобы получить примерные цифры, допустим, что площадь антенной системы ракеты составляет 1 м2, в то время как площадь наземной антенной системы в сто раз больше.
Если за минимальную силу сигналов [7], необходимых для приема, принять следующие данные:
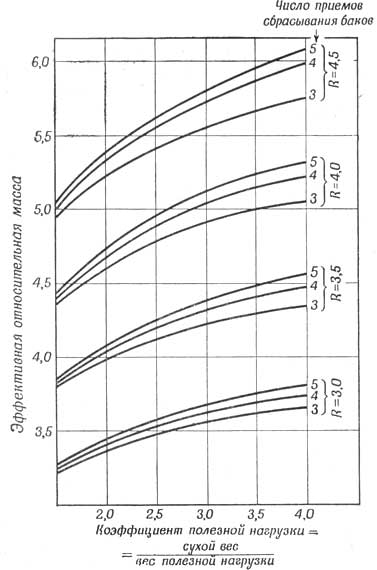 Фиг. 99. Эффективная относительная масса, получаемая при „отделяющейся" конструкции. Значительное увеличение эффективной относительной массы возможно только в том случае, если топливные баки будут сбрасываться в несколько приемов. |
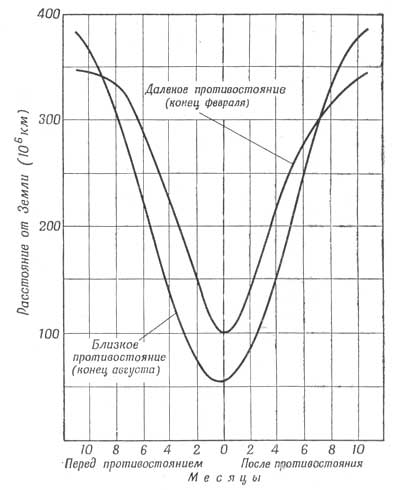 Фиг. 100. Расстояние между Землей и Марсом перед противостоянием и после него. |
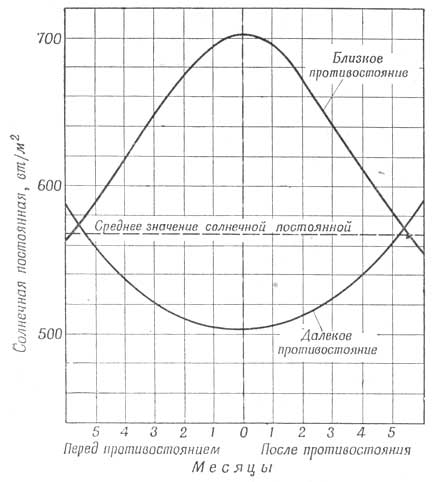 Фиг. 101. Изменение солнечной постоянной при движении по орбите Марса перед противостоянием и после него. |
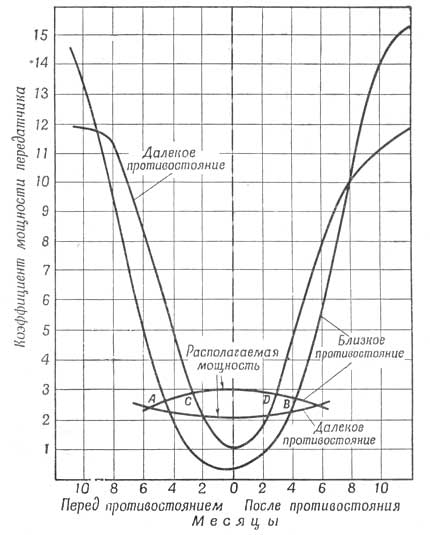 Фиг. 102. Потребная мощность передатчика перед противостоянием и после него (мощность при далеком противостоянии принята за единицу). |
Таблица 12

 Фиг. 103. Предполагаемый вид искусственного спутника Земли, предназначенного для наблюдений за Солнцем. Зеркало собирает энергию солнечного излучения для силовых установок и спектроскопических синоптических измерений. Антенная система направлена в сторону Земли. |
Даже при близких противостояниях невозможно передать по телевидению изображение поверхности какой-либо планеты. Однако Кросс показал [8], что при употреблении системы передачи развернутого изображения поверхности планеты методом электрической передачи
изображения потребуется только средняя мощность. Когда ракета будет проходить вблизи Марса, делая 6,83 полных обращений, оптическая развертка захватит полосу шириной в несколько километров, что постепенно позволит составить подробную карту поверхности на наземном приемном конце радиолинии. Таким образом, задолго до того, как удастся построить астрономическую обсерваторию на спутнике Земли, можно будет снарядить приборы для получения подробных фотографий поверхностей планет.
Аналогично, посылая ракеты в межпланетное пространство и передавая данные на Землю с помощью телеизмерительных устройств, можно собрать сведения об атмосферах планет, не снаряжая специально для этого космические корабли с экипажем. В связи с рядом технических и экономических затруднений, мы, по-видимому, еще долгое время не сможем быть свидетелями полета ракет с экипажем, а поэтому в течение ближайших пятидесяти лет ракеты-зонды будут являться самым совершенным средством астрономических и астрофизических исследований. Более того, такие ракеты-зонды послужат примером для будущих космических кораблей с экипажем, которые, несомненно, будут созданы в течение следующего столетия.
1. Grimm inger G., /. Appl. Phys., 19, 947 (1948).
2. Ovenden M. W., /. Brit. Interpl. Soc, 6, 157 (1947); 10, 275 (1951).
3. Gold Т., Proc. Gassiot Comm., Oxford, 1963.
4. Hohmann W., Die Erreichbarkeit der Himmelskorper, Oldenbourg, 1925.
5. Burgess E., Aeronautics, 27, 26 (1952).
6. Burgess E. and Cross С A.,I. Brit. Interpl. Soc, 12, 72 (1963)
7. Clarke А. С, Л Brit. Interpl. Soc, 7, 49 (1948).
8. Burgess E., Aeronautics, 21, 70 (1949).
9. Burgess E., Engineer, 193, 456 (1951).
10. Сarter L. J. (ed.), Proc. Il-nd Intern. Congr. Astronautics, 1961.